Linear programming in matlab

INTERNATIONAL JOURNAL Research and Development (IJIERD), ISSN 0976 –
International Journal of Industrial Engineering OF INDUSTRIAL ENGINEERING
6979(Print), ISSN 0976 – 6987(Online) Volume 4, Issue 1, January - April (2013), © IAEME
RESEARCH AND DEVELOPMENT (IJIERD)
ISSN 0976 – 6979 (Print)
ISSN 0976 – 6987 (Online)
Volume 4, Issue 1, January - April (2013), pp. 19-24
IJIERD
© IAEME: www.iaeme.com/ijierd.asp
Journal Impact Factor (2013): 5.1283 (Calculated by GISI) ©IAEME
www.jifactor.com

LINEAR PROGRAMMING IN MATLAB

Flt Lt Dinesh Kumar Gupta
Department of Mechanical Engg, Lovely Professional University, Phagwara (Punjab)
India

ABSTRACT

Since the late 1940s, linear programming models have been used for many different
purposes. Airline companies apply these models to optimise their use of planes and staff.
NASA has been using them for many years to optimize their use of limited resources. Oil
companies use them to optimise their refinery operations. Small and medium-sized
businesses use linear programming to solve a huge variety of problems, often involving
resource allocation.

In this paper, a typical product-mix problem in a manufacturing system producing two
products (each product consists of two sub-assemblies) is solved for its optimal solution
through the use of the latest versions of MATLAB having the command simlp, which is very
much like linprog. As analysts, we try to find a good enough solution for the decision maker
to make a final decision. Our attempt is to give the mathematical description of the product-
mix optimization problem and bring the problem into a form ready to call MATLAB’s simlp
command. The objective of this paper is to find the best product mix that maximizes profit.
The graph obtained using MATLAB commands, give the shaded area enclosed by the
constraints called the feasible region, which is the set of points satisfying all the constraints.
To find the optimal solution we look at the lines of equal profit to find the corner of the
feasible region which yield the highest profit. This corner can be found out at the farthest line
of equal profit which still touches the feasible region.

Keywords: Constraints, Decision variables, Duality, Feasible region, Optimization and
Operating expenses

1. INTRODUCTION

One of the most widespread commercial applications of scientific computation is
linear programming. It is widely used for allocating resources to achieve an objective. Here,

19

International Journal of Industrial Engineering Research and Development (IJIERD), ISSN 0976 –

in this paper the product-mix problem illustrated as a prototype example [1] refers to a
manufacturing system which may occur in real life applications is being solved through
MATLAB. The figure 1 represents a manufacturing system producing two products labeled P
and Q. The rounded rectangles at the top of the figure indicate the revenue per unit and the
maximum sales per week. For instance we can sell as many as 100 units of P for $90 per unit.
The circles show the raw materials used, and the rectangles indicate the operations that the
products must pass through in the manufacturing process. Each rectangle designates a
machine used for the operation and the time required.
For example product P consists of two subassemblies. RM stands for raw material .To
manufacture the first subassembly, one unit of RM1 passes through machine A for 15
minutes. The output of machine A is moved to machine C where it is processed for 10
minutes. The second subassembly starts with RM2 processed in machine B for 15 minutes.
The output is taken to machine C for 5 minutes of processing. The two subassemblies are
joined with a purchased part in machine D. The result is a finished unit of P. Product Q is
manufactured by a similar process as indicated in the figure1.

P Q

Fig 1

20


The rectangle at the upper left indicates that one machine of each type is available. Each
machine operates for 2400 minutes per week. OE stands for operating expenses. For this case the
operating expenses, not including the raw material cost is $6000. This amount is expended
regardless of amounts of P and Q produced. Our problem is to find out the product mix that
maximizes profit using MATLAB software.

2. FORMULATION OF LINEAR PROGRAMMING MODEL

Let X= Number of P products produced per week
Y= Number of Q products produced per week

Max Z = 45X + 60Y (Weekly revenue)
subject to
15X + 10Y ≤ 2400 (Machine A)
15X + 30Y ≤ 2400 (Machine B)
15X + 5Y ≤ 2400 (Machine C)
10X + 5Y ≤ 2400 (Machine D)
X ≤ 100 (Product P)
Y ≤ 50 (Product Q)
X≥ 0,Y≥ 0 (Nonnegativity)

3. SOLUTION USING MATLAB

Since there are only two unknowns involved, we may graph all constraints. The
MATLAB commands [2] given are as follows:

x=0:160 % range of graph
y1=(2400-15.*x)./10; % 15x+10y ≤2400 machine A
area(x,y1)
y2=max((2400-15.*x)./30,0); % 15x+30y ≤2400 machineB
y3=max((2400-15.*x)./5,0); % 15x+5y ≤2400 machineC
y4=max((2400-10.*x)/5,0); % 10x+5y ≤ 2400 machine D
y5=max((100-1.*x)./0,0); % 1x+0y ≤ 100 market constraint P product
y6=max((50-0.*x)./1,0); % 0x+1y ≤ 50 market constraint Q product
ytop=min([y1;y2;y3;y4;y5;y6]); % array of minima
area(x,ytop); % filled area plot

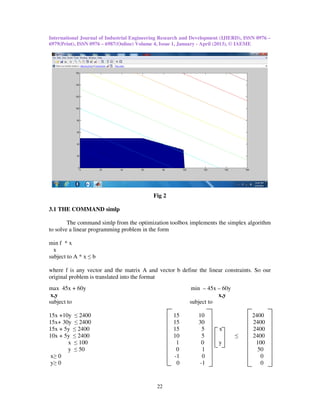
The shaded area enclosed by the constraints is called the feasible region, which is the set of points
satisfying all the constraints. If this region is empty, then the problem is said to be infeasible, and
it has no solution. The lines of equal profit Z are given by Z = 45x + 60y. If we fix Z to, say 100,
then all points (x; y) which satisfy 45x + 60y yield the same profit 100.

hold on;
[u v]=meshgrid(0:160,0:160);

contour(u,v,45*u+60*v);
hold off;
To find the optimal solution, we look at the lines of equal profit to find the corner of the
feasible region which yields the highest profit. This corner can be found at the farthest line of
equal profit which still touches the feasible region as shown in Fig 2.

21


Fig 2

3.1 THE COMMAND simlp

The command simlp from the optimization toolbox implements the simplex algorithm
to solve a linear programming problem in the form

min f * x
x
subject to A * x ≤ b

where f is any vector and the matrix A and vector b define the linear constraints. So our
original problem is translated into the format
max 45x + 60y min – 45x – 60y
x,y x,y
subject to subject to

15x +10y ≤ 2400 15 10 2400
15x+ 30y ≤ 2400 15 30 2400
15x + 5y ≤ 2400 15 5 x 2400
10x + 5y ≤ 2400 10 5 ≤ 2400
x ≤ 100 1 0 y 100
y ≤ 50 0 1 50
x≥ 0 -1 0 0
y≥ 0 0 -1 0

22


Observe the switching of signs to turn the max into a min and to deal with the ≤ constraints.
Duality in linear programming is a very important concept, more than just a matter of formatting.
The economical interpretation of duality can be simplified into the saying that minimizing the
cost of production is equivalent to maximizing the profit.
Now we are ready to solve the problem. First we set up the vectors and matrices:
f=[-45 -60]
A=[15 10; 15 30;15 5; 10 5; 1 0; 0 1; -1 0; 0 -1]
b=[2400; 2400; 2400; 2400; 100; 50; 0; 0]

The optimization toolbox has the command simlp :

simlp(f,A,b) % optimize
-f*ans % compute profit

f=

-45 -60

A=

15 10
15 30
15 5
10 5
1 0
0 1
-1 0
0 -1

b=

2400
2400
2400
2400
100
50
0
0

ans =

100
30

ans =

6300

23


4. CONCLUSION

The objective of this research work in finding the maximum units of products for
product mix problem is achieved. The final result as derived using MATLAB are as follows:
The values obtained are X = 100 units and Y= 30 units which mean that for the product mix
to optimize profits the manufacturer should produce 100 units of P products per week and 30
units of Q products per week. The net profit would be equal to maximum revenue, Z minus
total operating expenses, OE which comes out to be $300 per week. The extensions of this
research work would be to identify bottlenecks and sensitivity analysis using Fuzzy
Algorithm which allows us to determine how “sensitive” the optimal solution is to changes
in data values. This includes analyzing changes in:
i) An Objective Function Coefficient (OFC)
ii) A Right Hand Side (RHS) value of a constraint.

REFERENCES

[1] Operations Research Models and Methods by Paul A Jensen
[2] B.R Hunt, R.L Lipsman and J.M. Rosenberg. A Guide to MATLAB, for beginners and
experienced users, Cambridge University Press, 2001
[3] Varun Shukla, Anand Handa and Arun Agarwal, “Spectrum Analysis by using MATLAB
Script” International journal of Electronics and Communication Engineering & Technology
(IJECET), Volume 3, Issue 1, 2012, pp. 69 - 75, ISSN Print: 0976- 6464, ISSN Online: 0976
–6472.
[4] Gopichand Allaka, Prasad Raju Kalidindi, Koteswara Rao S, Manibabu Daadi and Abhay
Patnala, “Design of Solid Shafts using MATLAB” International Journal of Mechanical
Engineering & Technology (IJMET), Volume 3, Issue 3, 2012, pp. 645 - 653, ISSN Print:
0976 – 6340, ISSN Online: 0976 – 6359.

24

Linear programming in matlab

More Related Content

Similar to Linear programming in matlab

More from IAEME Publication

Linear programming in matlab