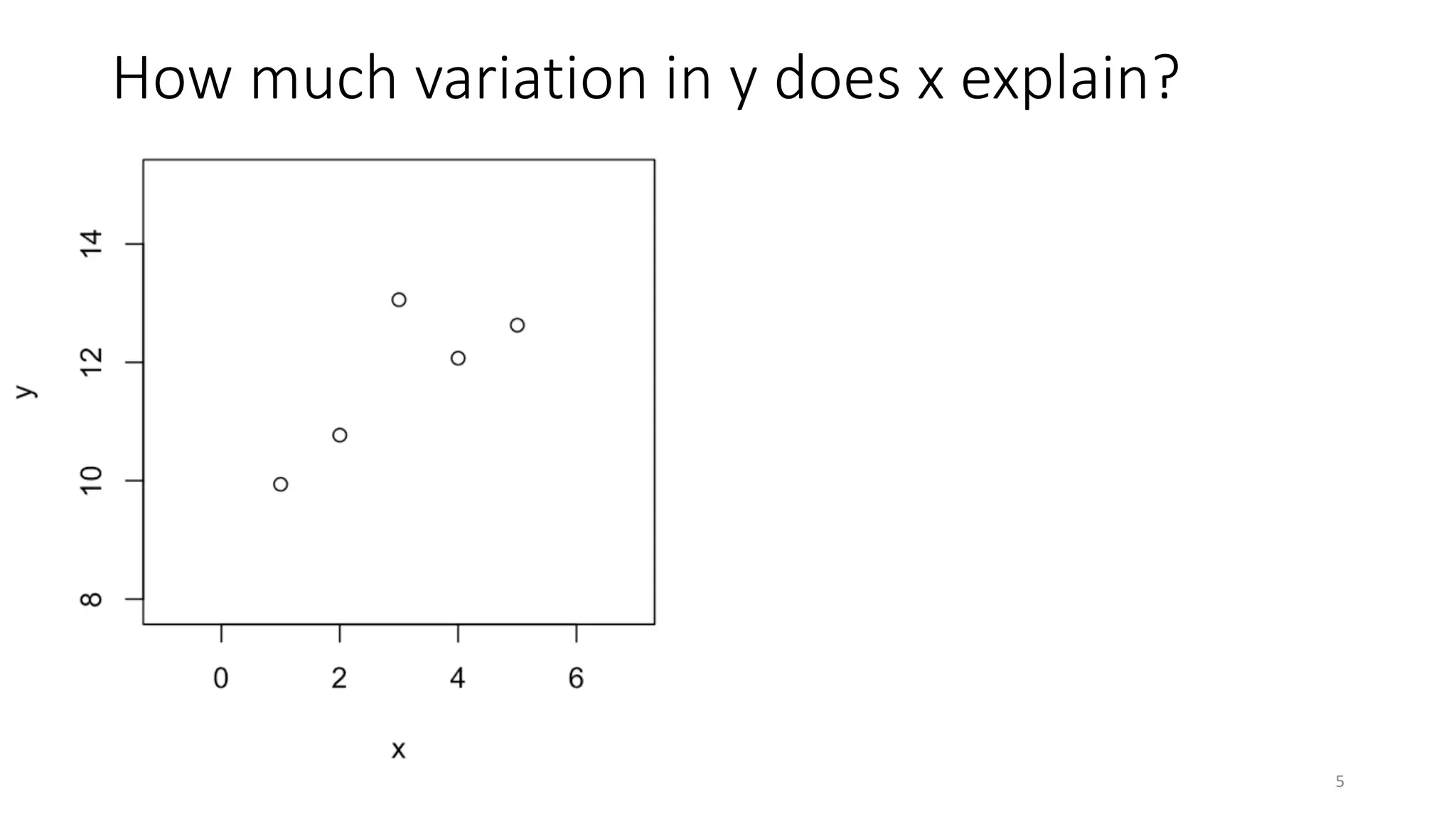
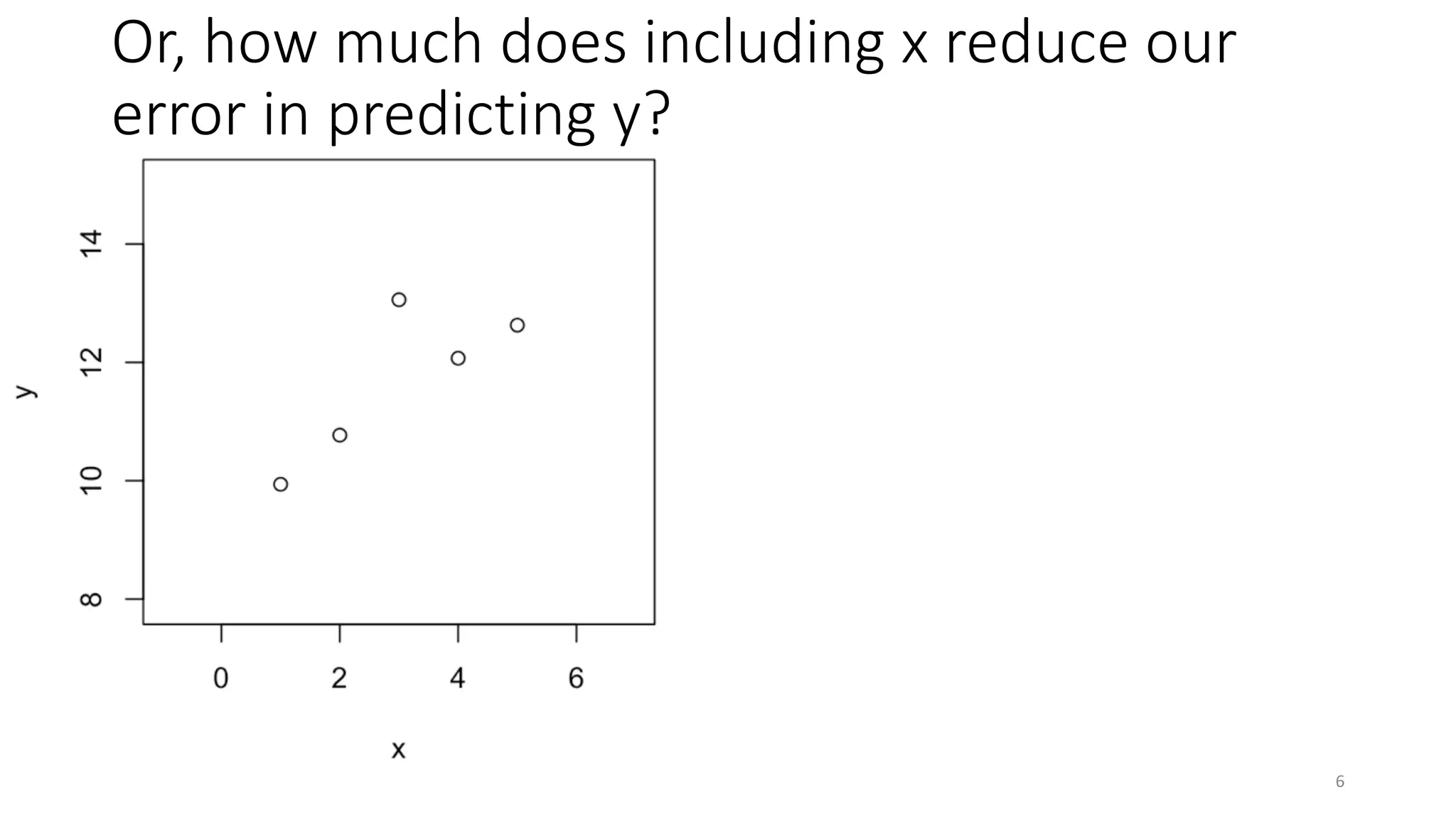
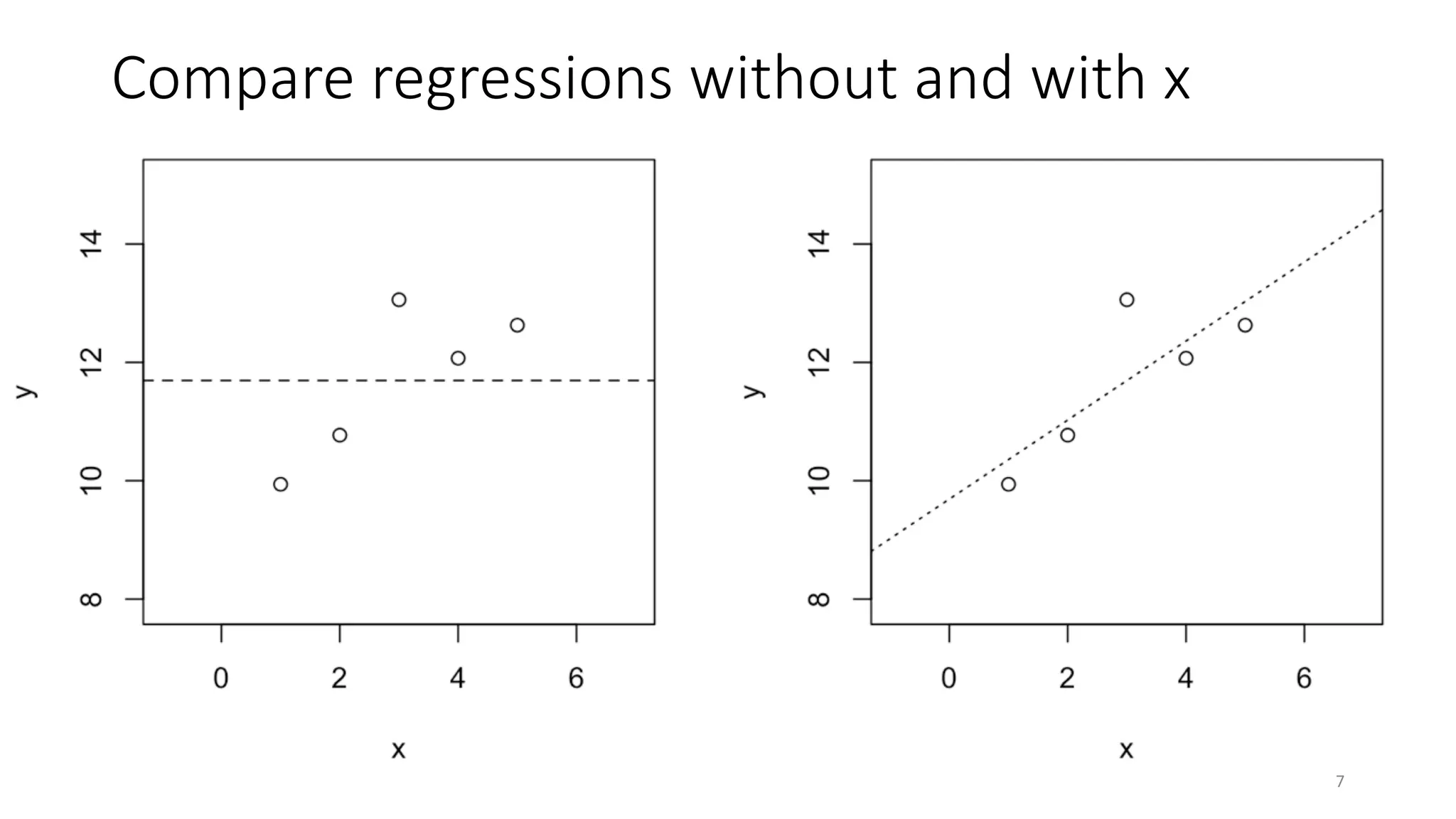
The document discusses the coefficient of determination, R², explaining its significance in assessing the goodness-of-fit of linear regression models, its limitations, and improvements in its application. It highlights the need for a focus on effect size measures over p-values and introduces frameworks for generalizing R² in generalized linear models and mixed-effects models. Overall, it emphasizes the importance of understanding R²'s limitations in predictive modeling and its adaptation for more complex statistical frameworks.

1. Extending R2 beyond
ordinary least-squares
linear regression
Paul Johnson
@paulcdjo
1

2. What this talk isn’t about
2

3. What this talk is about
• What is R2?
• Why is R2 useful?
• What are some of the limitation of R2?
• How have these limitations been overcome?
3

4. The coefficient of determination, R2
• R2 assesses goodness-of-fit of a linear regression model, on a scale
from 0 to 1
• Definitions
• Prediction: proportional reduction in model prediction error
• Explanation: proportion of variance in response variable explained
by explanatory variables
• R2 is a measure of how much better we understand a system
once we’ve measured and modelled some of its components
4

5. How much variation in y does x explain?
5

6. Or, how much does including x reduce our
error in predicting y?
6

7. Compare regressions without and with x
7

8. Gauge unexplained variation using the
squared prediction errors
8
Model without x
Model with x

9. Gauge unexplained variation using the
squared prediction errors
9

10. Including x has reduced total squared
prediction error
x
10

11. Including x has reduced total squared
prediction error to 34% of the “no x” total…
= 34%
11

12. R2 is the % reduction in prediction error:
= 66%R2 = 1 -
12

13. We can partition the previously unexplained
variance into explained (model) and unexplained
13

14. We can partition the (previously) unexplained variance
into explained (model) and unexplained (error)
= +
14

15. We can partition the (previously) unexplained variance
into explained (model) and unexplained (error)
= +
R2 = 1 - = = 66%
15

16. 1
b
a
e1
e1
e1
e1
e1
= +
16

17. Is R2 useful?
17

18. Rising complexity and falling explanatory power in ecology (Low-Décarie
et al. 2014 Frontiers in Ecology & the Environment)
18

19. Rising complexity and falling explanatory power in ecology (Low-Décarie
et al. 2014 Frontiers in Ecology & the Environment)
“If we extrapolate the current rate of decline …
we would make the improbable but alarming
prediction that ecology’s marginal explanatory
power will be zero within the next 100 years”
19

20. A crisis of irreproducibility?
20

21. Most important question in stats?
Is it a big
number?
21

22. Most important question in stats?
Is it a big
number?
22
We should be focusing less
(or at least not solely) on
P-values and more on
effect size measures such
as R2.

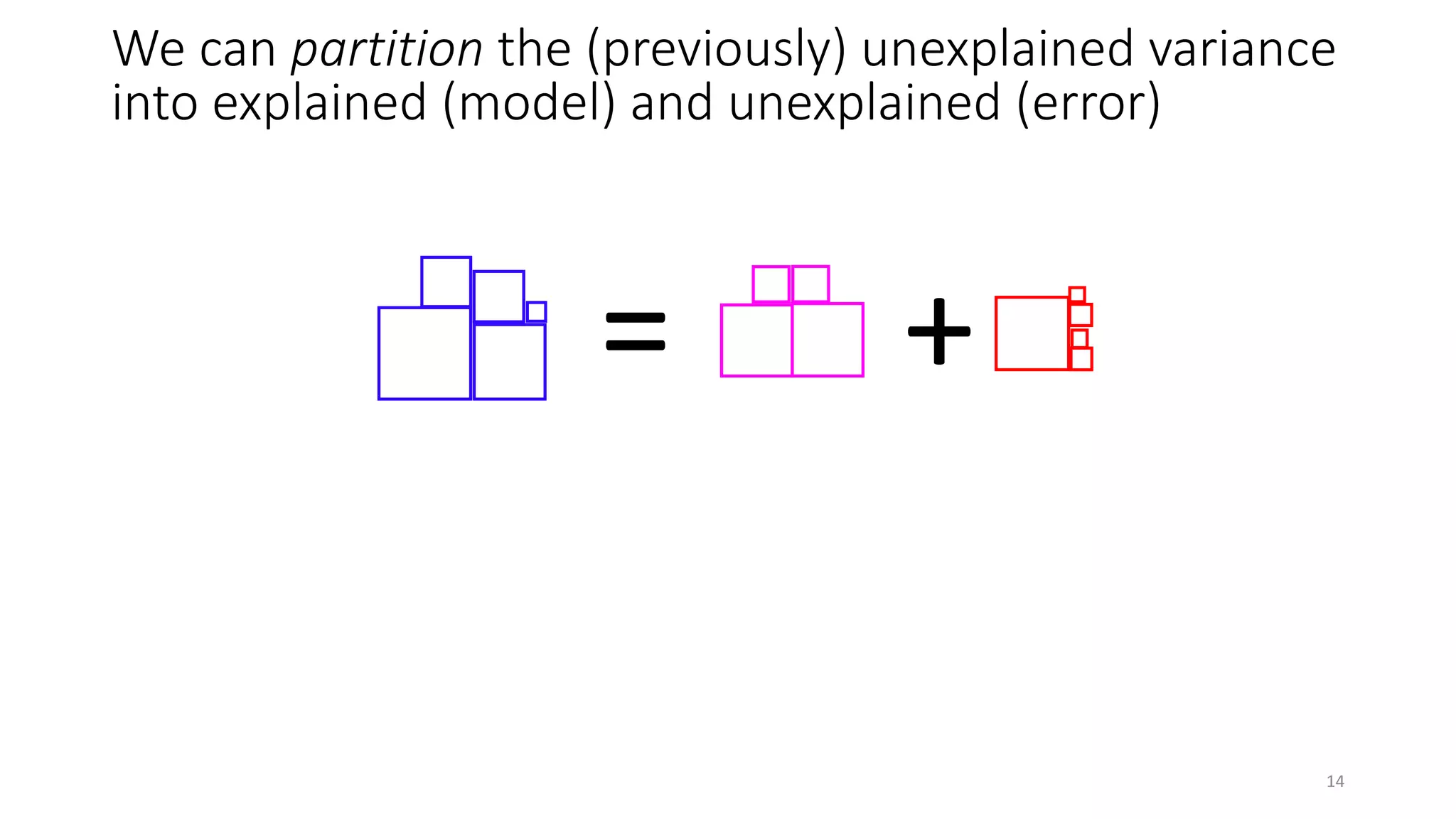
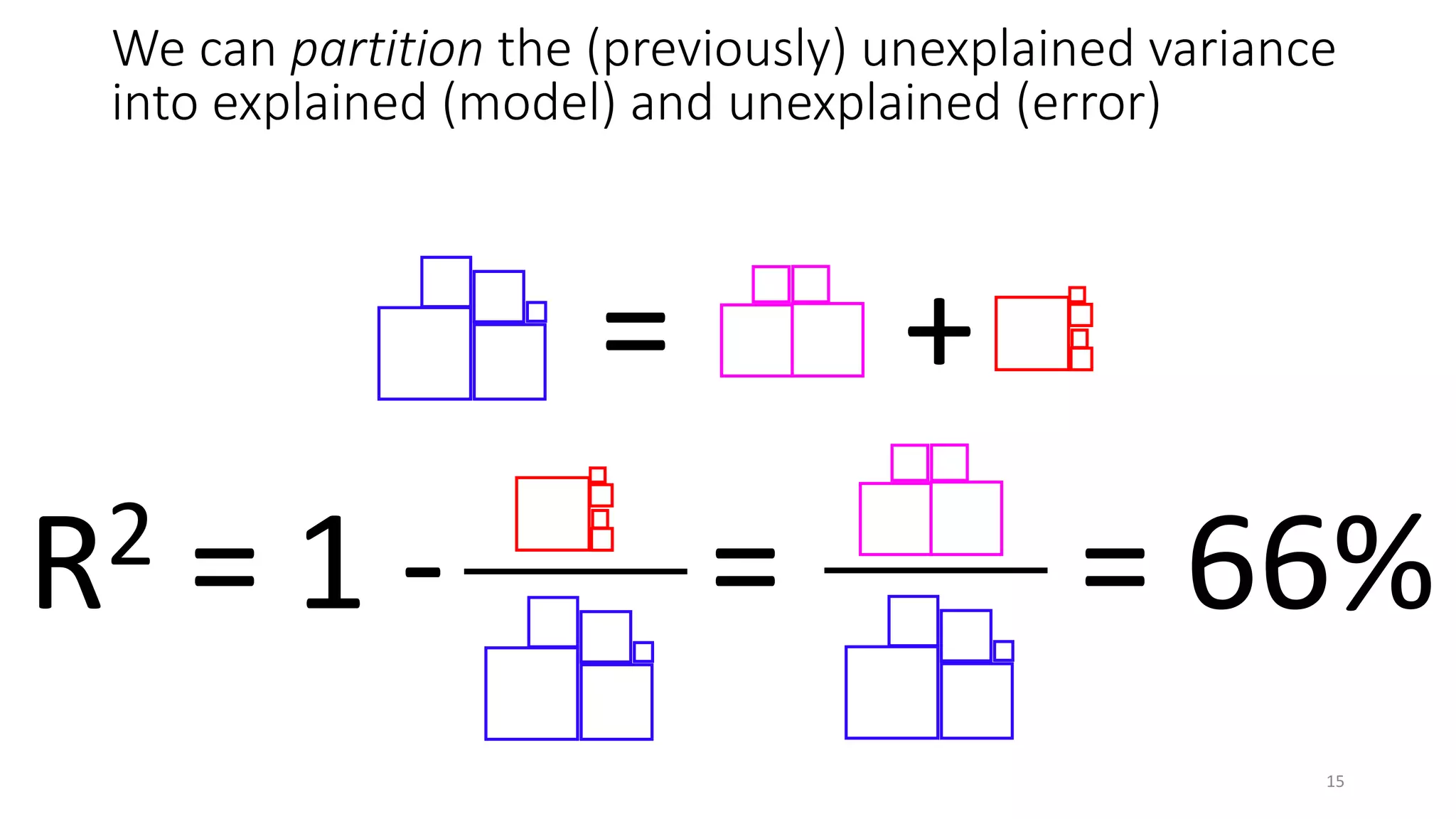
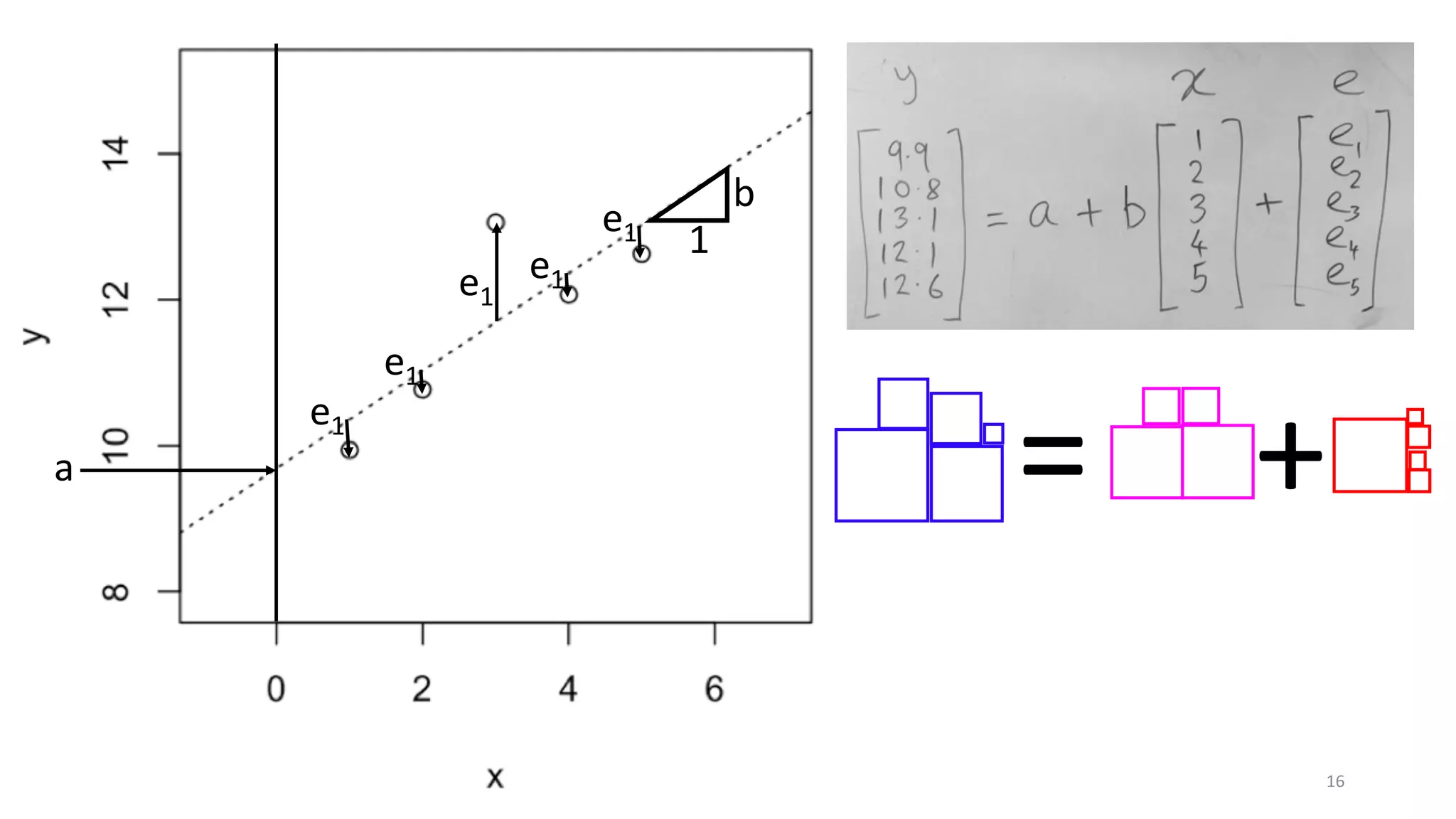
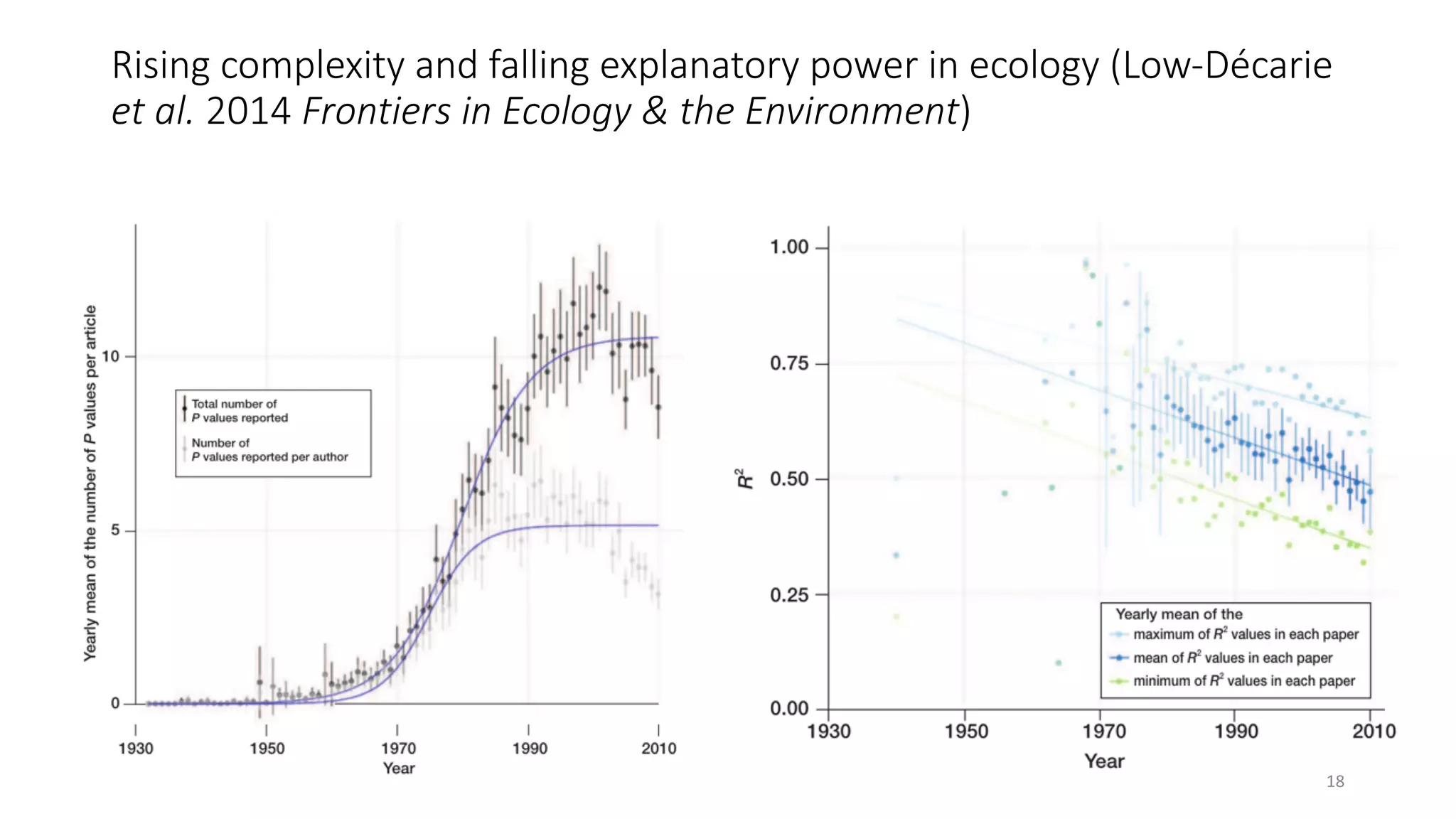
23. Limitations of R2
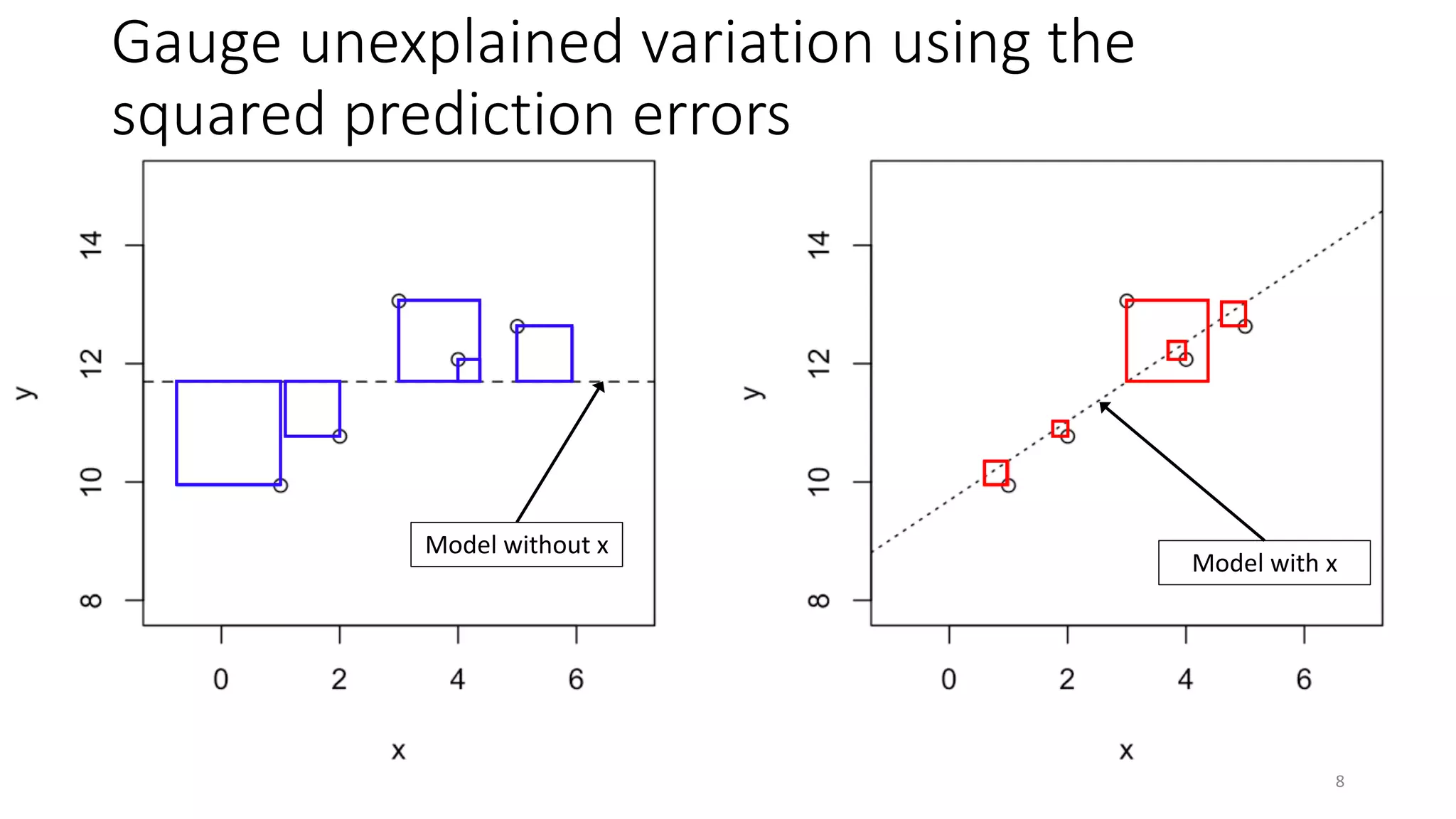
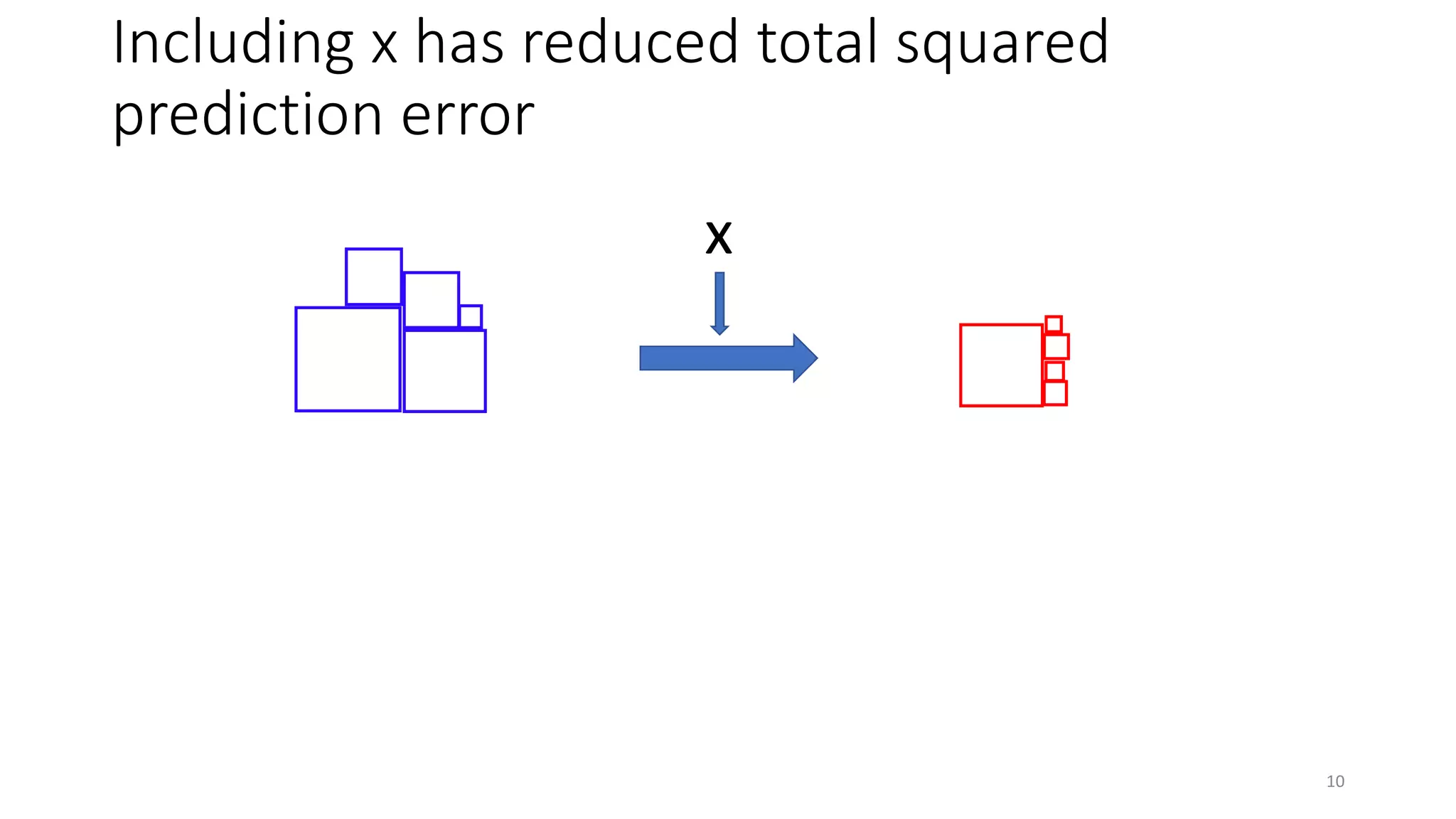
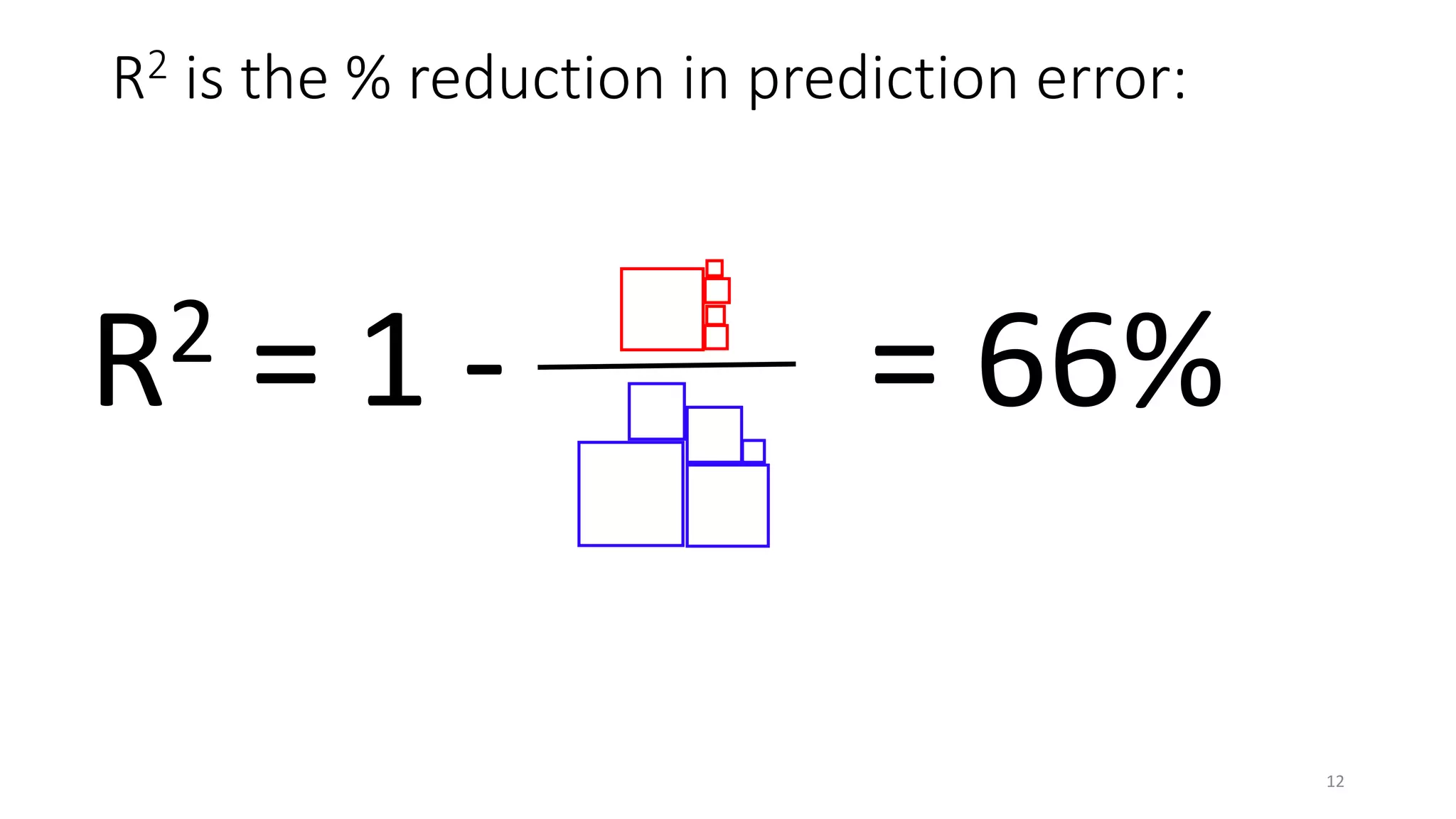
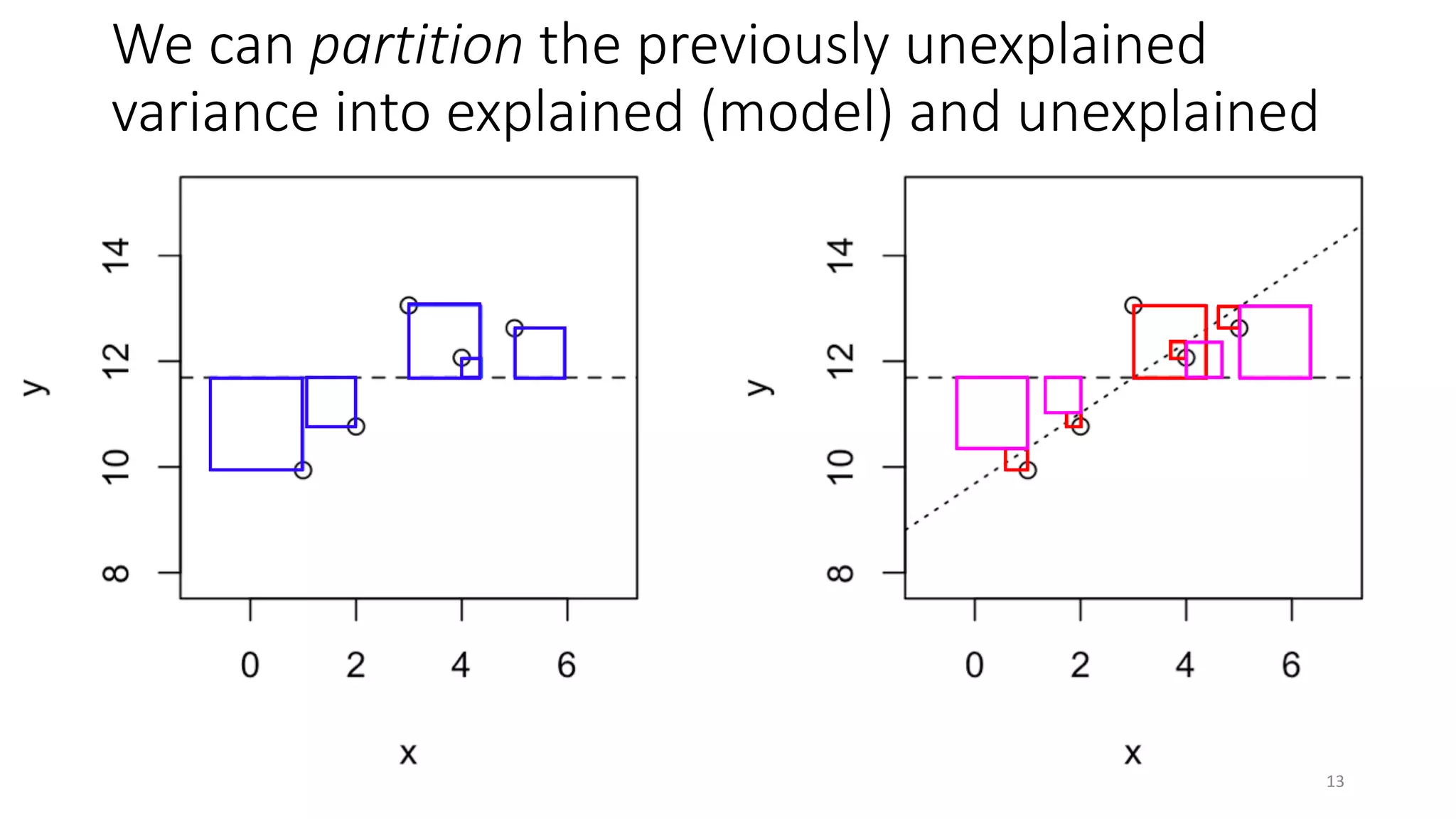
• Gauges error in predicting your own data – not actually prediction
• Using R2 for model selection will always select the largest model
• Adjusted R2 penalises model complexity (here n = 5, p = 1):
• R2
adj = 1 – (1 – R2) (n – 1) / (n – p – 1)
• R2
adj = 100% – 34% x 4/3 = 54%
• Adjusted R2 still can’t be used for model selection (but still is)
• We want the “best” model also to have the maximum R2, similarly to
minimising AIC. This is “Final Prediction Error” R2 (Nicoleta & Goşoniu
2006):
• R2
FPE = [(n+p+1) x R2
adj - p] / (n + 1)
• R2
FPE = (7 x R2
adj – 1) / 6 = 46% (the most “honest” R2 , cf R2 = 66%!)
23

24. Limitations of R2
• Not clear how to generalise beyond linear regression models
• Generalised linear models (GLM)
• Linear mixed-effects models (LMM)
• Generalised linear mixed-effects models (GLMM = GLM + LMM)
24

25. • Reviewed previous generalisations
of R2
• Proposed framework for R2 for
GLMMs based on variance
components
25

26. A random-intercepts Poisson GLMM
!"# ~ %&'( )"#
)"# = +,-.
/"# = 01 + 3
456
0474"# + 8#
8#~9 0, <=
>
26

27. A random-intercepts Poisson GLMM
!"# ~ %&'( )"#
)"# = +,-.
/"# = 01 + 3
456
0474"# + 8#
8#~9 0, <=
>
?@ABB(4)
>
=
<E
>
<E
>
+ <=
>
+ <F
>
27

28. A random-intercepts Poisson GLMM
!"# ~ %&'( )"#
)"# = +,-.
/"# = 01 + 3
456
0474"# + 8#
8#~9 0, <=
>
?@ABB(4)
>
=
<E
>
<E
>
+ <=
>
+ <F
>
28

29. A random-intercepts Poisson GLMM
!"# ~ %&'( )"#
)"# = +,-.
/"# = 01 + 3
456
0474"# + 8#
8#~9 0, <=
>
?@ABB(4)
>
=
<E
>
<E
>
+ <=
>
+ <F
>
29

30. A random-intercepts Poisson GLMM
!"# ~ %&'( )"#
)"# = +,-.
/"# = 01 + 3
456
0474"# + 8#
8#~9 0, <=
>
?@ABB(4)
>
=
<E
>
<E
>
+ <=
>
+ <F
>
30

31. • Reviewed previous generalisations
of R2
• Proposed framework for R2 for
GLMMs based on variance
components
31

32. • Limitations
• Doesn’t work for random-slopes
models
• Not available for certain
distributions, inc. negative
binomial and gamma
32

33. 2017
2014
R> library(piecewiseSEM) # by Jon Lefcheck
R> rsquared(glmer.mod)
Class Family Link n Marginal Conditional
1 glmerMod binomial logit 1431 0.5589205 0.629198 33

34. Thank you for listening
34