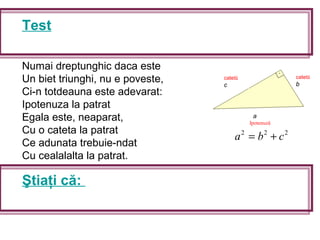
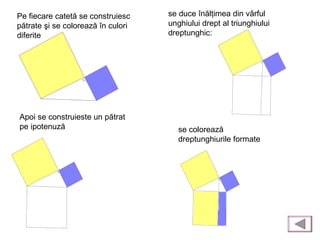
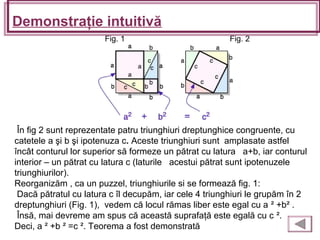
Teorema lui Pitagora stabilește că într-un triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei. Documentul detaliază demonstrații atât intuitive cât și matematice, oferind exemple de aplicație pentru a calcula lungimile catetelor și ipotenuzei. De asemenea, se menționează istoria teoremei și aplicarea acesteia în geometrie.

1. TEOREMA LUI
PITAGORA
a
c b
222
cba +=

2. Completaţi textul:
Într-un triunghi dreptunghic, pătratul …………..este egal
cu ………… pătratelor ………………….
Demonstraţie intuitivă
Teorema lui Pitagora
Teorema lui Pitagora este una dintre
cele mai cunoscute teoreme din
geometria plană .
Teorema lui Pitagora afirmă că:
"într-un triunghi dreptunghic,
suma pătratelor catetelor este
egală cu pătratul ipotenuzei".
a
Ipotenuză
catetă
c
catetă
b
222
cba +=

3. Demonstraţie matematică:
• Fie triunghiul dreptunghic
ABC, m(‹A)=90°.
Construim perpendiculara
din A pe latura opusă BC
şi fie D piciorul acestei
perpendiculare.
Triunghiul ABC fiind
dreptunghic putem aplica
teorema catetei, de două
ori, pentru fiecare din
catetele sale.
• Pentru cateta AC,
obţinem:
AC²=CD·CB (1)
Pentru cateta AB, obţinem:
AB2=DB·BC (2)
Adunând relaţiile (1) şi (2)
obţinem:
AC²+AB²=CD·CB+DB·BC
AC² +AB²=BC·(CD+DB)
AC²+AB²=BC²(q.e.d)
Alta demonstraţie
B
A
C
D

4. 1.Fie triunghi ABC dreptunghic în A:
a) Dacă lungimile catetelor AB şi AC sunt 4cm, respectiv
3cm, determinaţi
lungimea ipotenuzei BC.
b) Dacă cateta AC=6cm, iar ipotenuza BC= 10cm,
determinaţi lungimea
catetei AB.
Rezolvare
Obs: teorema lui Pitagora poate fi folosită şi pentru
determinarea lungimii unei catete:
Pătratul lungimii unei catete este egal cu diferenţa
dintre pătratul lungimii ipotenuzei şi pătratul lungimii
celeilalte catete.
Probleme

5. 2. Un triunghi dreptunghic are o catetă cu lungimea
de 3 cm, şi unghiul care se opune ei de 300.
Calculaţi lungimile ipotenuzei, a celeilalte catete şi a
înălţimii corespunzătoare ipotenuzei
Rezolvare
ProblemeProbleme

6. Test
Numai dreptunghic daca este
Un biet triunghi, nu e poveste,
Ci-n totdeauna este adevarat:
Ipotenuza la patrat
Egala este, neaparat,
Cu o cateta la patrat
Ce adunata trebuie-ndat
Cu cealalalta la patrat.
Ştiaţi că:
a
Ipotenuză
catetă
c
catetă
b
222
cba +=

7. • Prof. ALUCULESEI EMANUELA
• STR. GEORGE ENESCU, NR. 45
• SAT MĂNĂSTIREA HUMORULUI
• COM. MĂNĂSTIREA HUMORULUI
• JUD. SUCEAVA
• Cod poştal: 727355
• PARTICIPARE : INDIRECTĂ
• emaal2000@yahoo.com
• 0727353574

8. Rezolvare problema 1
a)
A
B C
a) Aplicăm teorema lui Pitagora astfel:
BC2 =AB2 +AC2
Înlocuim:
BC2= 42+32
BC2 = 16+9
BC2 = 25cm, de unde BC= 5cm.
4cm
3cm

9. A
B C
b) Aplicăm teorema lui Pitagora astfel:
AB2 = BC2 -AC2
Înlocuim:
AB2= 102 -62
AB2 = 100-36
AB2 = 64cm, de unde AB= 8cm.
6cm
10cm
b)

10. Rezolvare problema 2
• În triunghiul
dreptunghic ABC,
aplicăm teorema lui
Pitagora astfel:
BC² =AB² +AC²
• Înlocuim:
62 = AB² +32
AB² = 36-9
AB² = 25 cm, de
unde AB= 5cm.
• În triunghiul
dreptunghic ADB:
AB=2·AD
AD=2,5cm.
A
B CD
În triunghiul dreptunghic ABC, avem:
BC=2·AC
(AC se opune unghiului de 300 şi BC este ipotenuza)
BC= 6cm
3cm
300

11. Scrieţi Teorema lui Pitagora pentru toate triunghiurile
dreptunghice din figura alăturată. Scrieţi în casetele de dialog
răspunsul corect.
Test

12. PITAGORA
Legenda spune că la şcoala care îi purta numele, Pitagora a introdus un sistem de
recompense: pentru fiecare teoremă demonstrată, un student primea o monedă de
aur. Unul din elevii săi silitori, după ce a acumulat o sumă oarecare s-a îndrăgostit de
geometrie şi-i cerea lui Pitagora noi şi noi teoreme pentru as le demonstra. Pitagora a
fost de acord, dar i-a cerut el studentului câte o monedă pentru fiecare nouă teoremă
prezentată. Şi nu după multă vreme monedele s-au întors la Pitagora.
Pitagora (c. 580 î.Hr. - c.500 î.Hr.) a fost un filozof şi
matematician grec, originar din insula Samos, care punea la
baza întregii realităţi teoria numerelor şi a armoniei. Ne-a lăsat
moştenire: sistemul zecimal, tabla înmulţirii şi faimoasa
teoremă care i-a fixat numele în nemurire.
Teorema era cunoscută de babilonieni cu un mileniu înainte de
Pitagora , demonstrată de el şi redemonstrată ulterior de 370
de ori. După ce a demonstrat teorema, de bucurie, Pitagora a
mers la ocolul vitelor şi a sacrificat o sută de boi graşi. Pe
aceştia i-a sacrificat şi i-a jertfit zeilor, ca mulţumire pentru
faptul că i-au inspirat faimoasa teoremă. Până noaptea târziu,
Pitagora a şezut împreună cu prietenele sale triunghiurile, iar
ele l-au glorificat şi i-au cântat:
„Pitagora ne-a dat teorema
Vitele-o ştiu pe propria piele,
Învaţ-o degrabă de teamă
Să n-ajungi să fii printre ele!”

13. Ştiaţi că:
• Egiptenii realizau unghiuri drepte cu ajutorul
funiei cu 12 noduri! Echidistant dispuse pe o
funie cele 12 noduri permiteau transformarea
funiei cu ajutorul unor ţăruşi într-un triunghi
dreptunghic cu laturile de 3, 4, 5. Se utiliza
astfel reciproca teoremei lui Pitagora.

14. Pe fiecare catetă se construiesc
pătrate şi se colorează în culori
diferite
Apoi se construieste un pătrat
pe ipotenuză
se duce înălţimea din vârful
unghiului drept al triunghiului
dreptunghic:
se colorează
dreptunghiurile formate

15. Demonstraţie

16. Demonstraţie intuitivă
În fig 2 sunt reprezentate patru triunghiuri dreptunghice congruente, cu
catetele a şi b şi ipotenuza c. Aceste triunghiuri sunt amplasate astfel
încât conturul lor superior să formeze un pătrat cu latura a+b, iar conturul
interior – un pătrat cu latura c (laturile acestui pătrat sunt ipotenuzele
triunghiurilor).
Reorganizăm , ca un puzzel, triunghiurile si se formează fig. 1:
Dacă pătratul cu latura c îl decupăm, iar cele 4 triunghiuri le grupăm în 2
dreptunghiuri (Fig. 1), vedem că locul rămas liber este egal cu a ² +b² .
Însă, mai devreme am spus că această suprafaţă este egală cu c ².
Deci, a ² +b ² =c ². Teorema a fost demonstrată
Fig. 1 Fig. 2

17. Teorema catetei
Teorema catetei: Într-un triunghi
dreptunghic, lungimea unei catete este
media geometrică a lungimii ipotenuzei
ipotenuzei şi a lungimii proiecţiei ei
ortogonale pe ipotenuză.