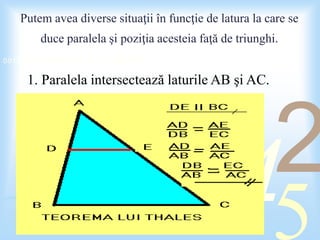
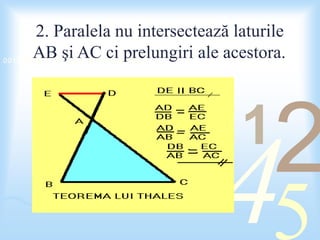
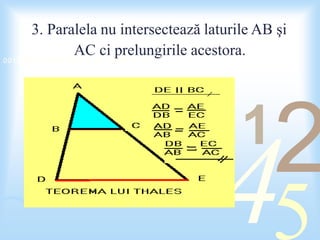
Thales din Milet, un matematician și filosof din Grecia antică, a formulat teoreme fundamentale și a pus bazele matematicii grecesti. Teorema lui Thales afirmă că o paralelă la una din laturile unui triunghi determină segmente proporționale pe celelalte două laturi. Documentul include o problemă de geometrie aplicând teorema lui Thales, însoțită de calcule și o bibliografie.

1. 5
1
0011 0010 1010 1101 0001 0100 1011
Motto : U
ng
a
n
de
s
t
eoi
d
e
ei
ntrecere
(Pitagora 580 i.e.n. - 500 i.e.n.)
Elev: Pinter Mario

2. 5
1
0011 0010 1010 1101 0001 0100 1011
TEOREMA LUI THALES

3. 5
1
0011 0010 1010 1101 0001 0100 1011
SCURT ISTORIC

4. 5
1
THALES DIN MILET
0011 0010 1010 1101 0001 0100 1011
Thales din Milet a fost declarat in anul 582 i.e.n. unul
dintre cei sapte intelepti ai antichitatii. A trait intre
anii 624 – 546 i.e.n. in Grecia antica si a fost un
recunoscut matematician, astronom si filozof.
A fondat in Milet cea mai veche scoala filozofica
materialista, de care este legata nasterea matematicii
grecesti.
Este primul matematician care a enuntat teoreme
insotite de demonstratii, ca :

5. 5
1
0011 0010 1010 1101 0001 0100 1011
• Diametrul imparte cercul in doua parti egale ;
• Unghiul inscris intr-un semicerc este drept (
teorema cunoscuta si de egipteni) ;
• Suma unghiurilor unui triunghi este de doua
unghiuri drepte ;
• Unghiurile de la baza unui triunghi isoscel sunt
egale ( fapt cunoscut si de egipteni si de babilonieni
) ;
• Congruenta triunghiurilor care au o latura si
unghiurile adiacente congruente ;
• Asemanarea triunghiurilor avand unghiurile
respectiv egale, in corelatie cu teorema care ii
poarta numele si care este enuntata astfel :

6. 5
1
0011 0010 1010 1101 0001 0100 1011
TEOREMA LUI THALES
TEOREMA:
O paralelă la una din laturile
unui triunghi determină pe
celelalte două laturi segmente
proporţionale.

7. 5
1
Putem avea diverse situaţii în funcţie de latura la care se
duce paralela şi poziţia acesteia faţă de triunghi.
0011 0010 1010 1101 0001 0100 1011
1. Paralela intersectează laturile AB şi AC.

8. 5
1
0011 0010 1010 1101 0001 0100 1011
2. Paralela nu intersectează laturile
AB şi AC ci prelungiri ale acestora.

9. 5
1
0011 0010 1010 1101 0001 0100 1011
3. Paralela nu intersectează laturile AB şi
AC ci prelungirile acestora.

10. 5
1
Analizând cu atenţie relaţiile date de teoerma lui
Thales, consatăm că, de fapt, ele sunt aceleaşi
0011 0
0
i1
n0
d1
i0
f1
e0
r1
e1
n0
1
t0
d0
e0
1
p0o10z0i1ţi0a1
1drepteiconstruite

11. 5
1
Proporţionalitatea segmentelor determinate de
paralelă pe laturile triunghiului înseamnă că
0011 0
0
l1
u0
n1
g0
1
i0
m1
i1
l0
e10
s0
e0
g1m0
1
0
e0
n1
t0
e1
l1
orde pe o latură se pot
obţine din lungimile segmentelor de pe cealaltă
latură prin înmulţire cu un număr real nenul,
adică:

12. 5
1
PROBLEMA REZOLVATA
0011 0010 1010 1101 0001 0100 1011
În triunghiul ABC, AB=36, AC=48, BC=60. Se
consideră D pe AB aşa încât AD=12 şi se duc
dreptele: DE paralelă cu BC, E pe AC, EF paralelă
cu AB, F pe BC, FG paralelă cu AC, G pe AB, GH
paralelă cu BC, H pe AC, HI paralelă cu AB, I pe
BC şi IK paralelă cu AC, K pe AB. Se cere lungimea
segmentului [DK].

13. 5
1
Construim figura corespunzatoare datelor
problemei:
0011 0010 1010 1101 0001 0100 1011

14. 5
1
Construind figura, constatăm că punctele K şi
0011 0
0
1
0
D1
0
c1
o0i1
n1
0
c1
id0
0
,0
s1
a0
u1
0
0
su1
0
n1
t1foarte apropiate, deci, s-
ar părea că DK=0. Să facem calculele
pentru a verifica acesată observaţie. Pentru
a nu complica inutil figura, vom scoate
separat, de fiecare dată, numai elementele
care ne interesează.

15. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 1.

16. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 2.

17. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 3.

18. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 4

19. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 5.

20. 5
1
0011 0010 1010 1101 0001 0100 1011
Pasul 6.

21. 5
1
0011 0010 1010 1101 0001 0100 1011

22. 5
1
Bibliografie
0011 0010 1010 1101 0001 0100 1011
 Surse internet:
http://ro.wikipedia.org/wiki/Thales_din_Milet
http://ro.wikipedia.org/wiki/Teorema_lui_Thales