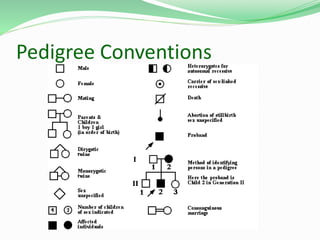
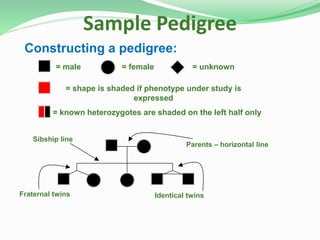
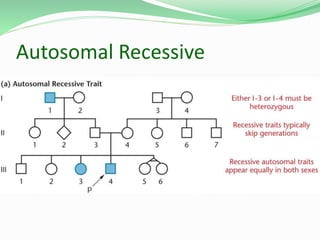
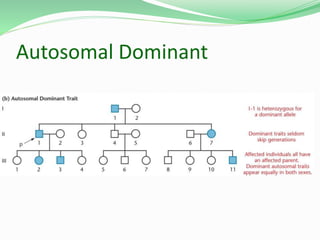
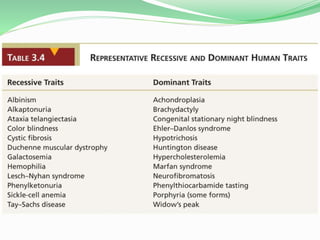
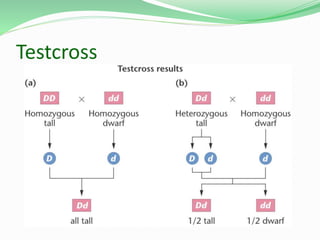
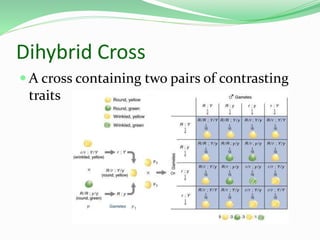
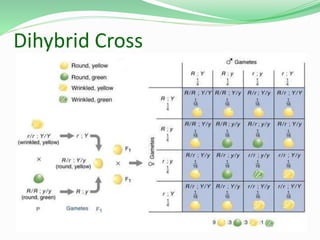
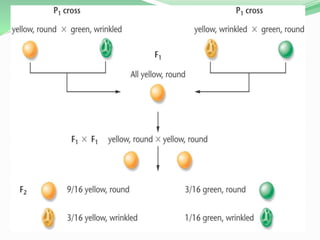
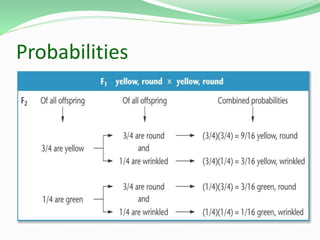
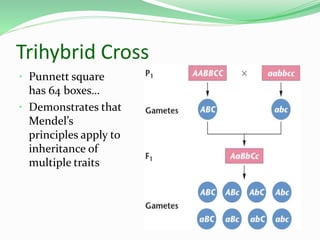
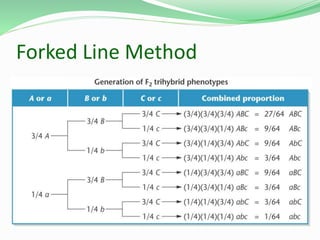
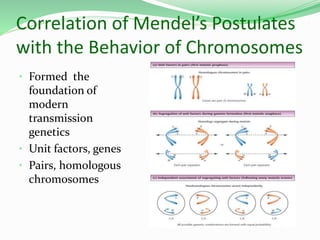
This document discusses Mendelian genetics and inheritance patterns. It covers Mendel's experiments with pea plants and his principles of inheritance, including dominance, segregation, independent assortment, and probability. It introduces modern genetic terminology and genetic crosses such as monohybrid, dihybrid, and test crosses. It also discusses how Mendel's principles apply to human pedigrees and inheritance of traits, including examples of autosomal recessive and dominant traits like familial hypercholesterolemia.

1. Chapter 3

2. Mendelian (Transmission) Genetics
 the transfer of genetic information from genes to
another generation (from parent to offspring)

3. Figure 3-1 Copyright © 2006 Pearson Prentice Hall, Inc.

4. Mendel’s Findings
• Determined there are distinct units of inheritance
• Behavior of units could be predicted during the
formation of gametes
• Later researchers linked the behavior of chromosomes
during meiosis to Mendel’s principles of inheritance
• The study of transfer of inheritance in this manner to
offspring is called Mendelian (or transmission) genetics

5. Monohybrid Cross

6. P  F1  F2

7. Monohybrid Cross

8. Reciprocal Crosses
 Shows if traits are sex-dependent

9. Reciprocal Crosses

10. Mendel’s three postulates
• (1) Unit factors in pairs
• (2) Dominance/Recessiveness
• (3) Segregation
• Random, gametes have equal chance

11. Modern Terminology
• Phenotype is the physical expression of a trait
• Mendel’s unit factors are now called genes
– Alternate forms of a gene are called alleles
– The first letter of recessive trait is used to symbolize
gene (d = dwarf, D = tall)

12. Modern Terminology
• Genotype refers to the actual alleles present
– Two unit factors are present in diploid individual
– Possible combinations - DD, Dd, or dd

13. Monohybrid
Cross
Figure 3-2 Copyright © 2006 Pearson Prentice Hall, Inc.

14. Punnett Square
 A Punnet square is a method for visualizing
combinations of gametes in a cross

15. Testcross

16. Dihybrid Cross
 A cross containing two pairs of contrasting
traits

17. Dihybrid Cross

18. Dihybrid Cross

19. Dihybrid Cross

20. Mendel’s 4th Postulate
• Results of Mendel’s dihybrid crosses can be
understood by considering the
probabilities separately
– COLOR: ¾ are yellow, ¼ are green
– SHAPE: ¾ are round, ¼ are wrinkled
– Use the product law of probability
 the combined probability of the two outcomes is
equal to the product of their individual
probabilities

21. Probabilities

22. Mendel’s 4th Postulate
– (4)Independent Assortment
 During gamete formation, segregating pairs of
unit factors assort independently of each other
 This means that all possible combinations of
gametes will be formed with equal frequency
 Final dihybrid ratio (assumes independent
assortment and random fertilization) is 9:3:3:1

23. Testcrosses with two characters

24. Trihybrid Cross
• Punnett square
has 64 boxes…
• Demonstrates that
Mendel’s
principles apply to
inheritance of
multiple traits

25. Forked Line Method

26. Useful Rules
Examples:
1. Aa [A, a]  [AA, Aa, aa]  [A or a]
2. AaBb  [AB, Ab, aB, ab]  [AABB, AaBB, aaBB, AABb,
AaBb, aaBb, aaBB, aaBb, aabb]  [AB, Ab, aB, BB]

27. Correlation of Mendel’s Postulates
with the Behavior of Chromosomes
• Formed the
foundation of
modern
transmission
genetics
• Unit factors, genes
• Pairs, homologous
chromosomes

28. Laws of Probability
• Genetic ratios are expressed as
probabilities
– Predict the outcome of each fertilization
event
 0 = certain not to occur
 1.0 = certain to occur
– In the Tall/dwarf monohybrid cross:
 3 out of 4 zygotes become tall (0.75)
 1 out of 4 zygotes are dwarf (0.25)

29. Laws of Probability
• Product Law
– Discussed in relation to independent assortment
– Probability of two or more outcomes occurring
simultaneously is equal to the product of their
individual probabilities
– Example: Coin toss (penny and nickel)
• Sum Law
– Generalized outcomes can be predicted by adding
probabilities (head/tails + tails/heads)

30. Laws of Probability
Sum Law (cont.)
• Example: one heads, one tails
 PH:NT = ¼
 PT:NH = ¼
 ¼ + ¼ = ½
• Sample Problem: In an F1 self-cross
(Tall/dwarf parents), what is the
probability that an F2 generation plant is
true-breeding (homozygous) for the trait

31. Laws of Probability
• Conditional Probability
– Probability of an outcome dependent on a specific
condition of that outcome
 Example: probability that any tall F2 plant from a
Tall/dwarf monohybrid cross will be heterozygous
 Condition is to consider only tall plants (we already
know that dwarfs are homozygous)
– pc = pa/pb (pa, probability of heterozygote, pb;
probability of dominant phenotype, pc;
probability of dominant phenotype being a
carrier)
– Can be applied to genetic counseling
 Chances if a “normal” person being a carrier

32. Binomial Theorem
– Used to calculate probability of outcomes
for any number of potential events
Binomial theorem: (a+b)n = 1
 a and b are respective probabilities of the two
alternate outcomes
 n = the number of trials
 a2 + 2ab + b2 [n = 2]
 a3+ 3a2b + 3ab2 + b3 [n = 3]
 a4 + 4a3b + 6a2b2 + 4ab3 + b4 [n = 4]

33. Pascal’s Triangle
– Expand the
binomial
– Determines the
numerical
coefficients
preceding each
expression

34. More Binomial Theorem
 Example: Probability of a family of four
having two boys and two girls
 Exponent of a represents # of boys
 Exponent of b represents # of girls
 p = 6a2b2
 Formula for determining numerical
coefficients for any set of exponents
 n!/(s!t!) where n = total # of events, s = # of times
a occurs and t = # of times b occurs
 “!” means factorial

35. Chi-Square Analysis
• Evaluates the Influence of Chance on Genetic Data
• Degrees of freedom
– Number of possible outcomes minus one (n - 1)

36. Chi-Square Analysis
• “Null Hypothesis” – assumes there is no real difference
between the measured (experimental) and predicted
values
– The apparent difference can be attributed to chance
(Null hypothesis “proven”)
– Null hypothesis “fails” if chance cannot reasonably
explain deviation from expected

37. Chi-Square Calculations

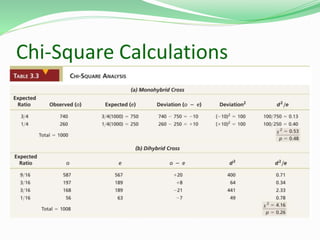
38. Figure 3-12ab Copyright © 2006 Pearson Prentice Hall, Inc.
[difference may be real]
Random variation

39. Interpreting X2 and p value
calculations
• What do p values mean????
• As 2 values increase, p values decrease
– Dihybrid cross, p = 0.26
 Then 26% of the time the value obtained from an experiment
would vary from the expected value by this much or more
based solely upon chance

40. Interpreting X2 and p value
calculations
– Traditionally a p value of 0.05 is the accepted standard to
accept the null hypothesis
 More than 0.05 is considered confirmatory (chance variation
is thus the likely explanation for any deviation from expected
results)
 Less than 0.05 means chance variation is an unlikely
explanation (though still a possible one, probability
depending upon the actual p value) – Null Hypothesis fails

41. Pedigrees reveal patterns of
inheritance in humans
• Pedigree
– Family tree
– Indicates presence or absence of trait in question for
each member

42. Pedigree Conventions
• Circles for females, squares for males
• Parents connected by horizontal line, offspring by
vertical lines connected to horizontal one
• Related parents (cousins) said to be consanguineous and
connected by double line
• Siblings written in birth order, left to right
• Generations indicated by Roman numerals
• Twins indicated by forked line, identical twins by fork
connected by horizontal line
• For single trait, shaded symbols indicate trait expressed
• Shaded with dot indicates known carriers
• Line through symbol indicates deceased

43. Pedigree Conventions

44. Sample Pedigree
Constructing a pedigree:
= male = female = unknown
= shape is shaded if phenotype under study is
expressed
= known heterozygotes are shaded on the left half only
Parents – horizontal line
Sibship line
Fraternal twins Identical twins

45. Pedigree
symbols and
notations

46. Autosomal Recessive

47. Autosomal Dominant

49. Familial Hypercholesterolemia
• Dominant
– but note varied phenotype of homozygote vs.
heterozygote
• LDL receptor for cholesterol uptake by cells
• Heterozygotes have about 2X LDL levels in blood,
heart attacks by 40 yrs common
• Homozygotes have no receptors, 10X LDL levels and
may have heart attach by 5 yrs of age, rarely survive to
age 20