Structural engineering formulas

SnnucrrlRAr', ExcrxnERrNG
tr'onuul-,AS
COMPRESSION . TENSION . BENDING . IIORSION . IMPACT
BNAMS ' FRAMES . ARCIIES . IIRUSSES . PLA.IES
FOUNDATIONS . RE||ATNING WALLS . PIPES AND TUNNELS
ILYA MrriHBr,soN, PII.D'
ILLL]SITRATIONS BY LIA MIKISLSON, M.S.
MCGRAW.HILL
NE$,YORI< CIIICAGO SNF'RANCISCO LISBON LONDON MADRID
MEXICO CITY MILAN NES'DEI,HI SAN JUAN SNOUL
SINGAPORT SYDNEY ITORONIIO
.'..

Library of Congress Catatoging-in-publication Data
Mikhelson, llya.
Structural engineering formulas / ilya Mikhelson.
p. cm.
tsBN 0-07-14391 1-0
1. Structural engine€ring-Mathematics. 2. Mathematics_Formulae. L Tifle.
TA636.M55 2004
624.1'02'12-4c22 2004044803
copyright @ 2004 by llya lvlikhelson. AII rights reserued. printed in the united states of America.
Except as permitted under the united states copyright Act of 1 976, no part of this publication may be
reproduced or distributed in any form or by any means, or stored in a data base or retrieval svstem.
without the prior written permission of the publisher.
1 234567 890 DOC/DOC 01 0987654
lsBN 0-07-14391 1-0
The sponsoring editor for this book was Larry s. Hager, the editing superyisor was stephen M. smith,
and the production supervisor was sherri souffrance. The art director for the cover was Maroaret
Webster-Shapiro.
Printed and bound by RR Donnelley
McGraw-Hill books are available at special quantity discounts to use as premiums and sales promotions,
or for use in corporate training programs. For more information, please write to the Direator of special
sales, Mccraw-Hlll Professional, Two p enn plaza, New york, Ny 1 0121-2298. or contact vour local
bookstore.
This book is printed on recycled, acid-free paper containing a minimum of 50% recycled,
de-inked fiber.
Information contained in this work has been obtained by The McGraw-Hill companies, Inc. (,,Mccraw-
Hill") from sources believed to be reliable. However, neither McGraw-Hill nor its authors guarantee the
accuracy or completeness of any information published herein and neither McGraw-Hill nor its authors
shall be responsible for any errors, omissions, or damages arising out of use of this information. This
work is published with the understanding that Mccraw-Hill and its authors are supplying information but
are not attempting lo render engineering or other professional services. lf such services are reouired.
the assistance of an appropriate professional should be sought.
To my wif e and son
:-

CONTE N s
Preface
Acknowledgments
Introduction
Basis of Structural Analysis
1. Stress and Strain. Methods ofAnalysis
Tension and compression
Bending
Combination of compression (tension) and bending
Torsion
Curved beams
Continuous deep beams
Dynamics, transverse oscillations of the beams
Dynamics, impact
2. Properties of Geometric Seciions
For tension, compression, and bending structures
For toFion structures
Statics
3. Beams. Diagrams and Formulas forVarious Loading Conditions
Simple beams
Simple beams and beams overhanging one support
Cantilever beams
Beams fixed at one end, supported at other
Beams fixed at both ends
Continuous beams
Continuous beams: settlement of support
Simple beams: moving concentrated loads (general rules)
Tables
't.1
1.2,1.3
'1.4
1.5
1.6
1.7
1.8-1.10
1.1',t,1.12
2.'t-2.5
2.6
3.1-3.3
3.4
3.5
3.6,3.7
3.8, 3.9
3.10
3.11
3.'12

CONTENTS CONTENTS
Bsams: influencs lines (exampl€s)
Eeams: computation of bending moment and shear using influene lines
(examples)
4, Framos. Diagrams and Formulas for Various Static Loadlng Conditions
5. Archos. Diagrams and Formulas for Various Loading Conditions
Three-hinged arches: support reactions, bending moment, and axial force
Symmetrical three-hinged arches of any shape: formulas for various static
loading conditions
Two-hinged parabolic arches: formulas for various static loading mnditions
Fixed parabolic arches: formulas for various static loading @nditions
Three-hinged arches: influen@ lines
Fixed parabolic arches: influence lines
Steel rope
6, Trusses. Method of Joints and Method of Section Analysis
Method ofjoints and method of section analysis: examples
Infl uence lines (examples)
7. Plates. Bending Moments for Various Support and Loading Conditions
Rectangular plates: bending moments | 2.1
Rectangular plates: bending moments (uniformly distributed load) | 7.2-T.s
Rectangular plates: bending moments and defloctions (uniformly distributed load) | 2.0
Rectangular plales: bending moments (uniformly varying load) | 7,7,1.9
Circular plates: bending moments, shear and defloction (uniformly distributed load) | 7,g
Soils and Foundations
8. Soils
3.13,3.14
3.15,3.16
4.14.5
5.1
5.2,5.3
5.4, 5.5
5.6,5.7
5.8
5.9
5.10
6.1,6.2
6.3,6.4
ilt.
Engineering properties of soils
Weighumass and volume relationships; flow of water in soil
8.1
8.2
IV
Stress distribution in soil
Settlement of soil
Shear strength of soil; slope stability analysis
Bearing capacity analysis
9. Foundations
Direct foundations
Direct foundation stability; pile foundations
Pile group capacity
Pile capacity
Rigid continuous beam elasti€lly supported
Retaining Structures
10. Retaining Structures
Lateral earth pressure on retaining walls
Lateral eadh pressure on braced sheetings; lateral earth pressure on
basement walls
11. Retaining Structures
Cantilever retaining walls; stability analysis
Cantilever sheet pilings
Anchored sheet pile walls
Pipes and Tunnels
1 2. Pipes and Tunnels. Bending Moments for Various Static Loading
Conditions
Rectangular cross-section
1 3. Pipes and Tunnels. Bending Moments for Various Static Loading
Conditions
Circular cross-section
8.3
8.4,8.5
8.6
8.7
9.1
9.2
9.3
9.4
9.5-9.7
10.1-10.5
10.6
11.1
11.2
11.3
V.
12.1-12.5
13.1-13.3

ONTENTS
Appendix
Units: conversion between Anglo-American and metric systems
Mathematical formulas: algebra
l4athematjcal formulas: geometry, solid bodies
Mathematical formulas; trigonometry
Symbols
u.1, u.2
M.1, M.2
M.3, M.4
M.5, M.6
s.1
PFIEFACE
This reference book is intended for those engaged in an occupation as important as lt is
interesting--{esign and analysis ofengineering structures. Engineering problems are diverse,
and so are the analyses they require. Some are performed with sophisticated computer programs;
others call only for a thoughtful application of ready-to-use formulas. ln any situation, the
informationinthiscompilationshouldbehelpful. ltwillalsoaidengineeringandarchitectural
students and those studying for licensing examinations.
llya N.4ikhelson, Ph.D

ACI(NO-wLEDGNIENTS
Deep appreciation goes to Mikhail Bromblin for his unwavering help in preparing the book's
illustrations for publication.
The author would also like to express his gratitude to colleagues Nick Ayoub, Tom Sweeney, and
Davidas Neghandi for sharing their extensive engineering experience.
Special thanks is given to Larry Hager for his valuable editorial advice.
INTFIODUCTION
Analysis of structures, regardless of its purpose or complexity, is generally performed in the
following order:
. Loads, both permanent (dead loads) and temporary (live loads), acting upon the structure are
computed.
. Forces(axisforces,bendingmoments,sheare,torsionmoments,etc.)resultinginthestructure
are determined.
o Stresses in the cross-sections of structure elem€nts are found.
. Depending on the analysis method used, the obtained results are compared with allowable
or ultimate forces and stresses allowed by norms.
The norms of structuEl design do not remain constant, but change with the evolving methods
of analysis and increasing strength of materials. Furthermore, the norms fof design of
various struclures, such as bridges and buildings, are different. Therefore, the analysis methods
provided in this book are limited to determination of forces and stresses. Likewise, the
included properties of materials and soils are approximations and may differ from those
accepted in the norms.
AII the formulas provided in the book for analysis of structures are based on the elastic theory.

About the Author
llya Mikhelson, Ph.D., has over 30 years'experience in design, research, and teaching design
of bridges, tunnels, subway stations, and buildings. He is the author of numerous other
publications, including: Precast concrete for Underyround Construction, Tunnels and Subways,
and Bu ild ing Stru cture s.
L. STFIESS
and
STFIAIN
Methods of Analysis

STRESS and STRAIN
Tables 1.1-1.1 2 provide formulas for determination of stresses in structural elements for various loading
conditions. To evaluate the results, it is necessary to comparc the computed stresses with existing
norm reouirements.
TENSION and COMPRESSION 1.1
eight
Diogroms
Axial force: N. = YA(L_x),
Y = unit volume weight,
A = cross - sectional area.
N
Stresses:o.=;!=f( t__x), o,,=TL. o. r=0.
Detbmation:
a =11(zr-*). a ^=0. ^ =-'}L.=IY-L
' 2E' 2E 2FA
W = yAL = weight of the beam
E = Modulus of elasticity
Axial force : tension, compressi
_-_4*-*
PP
Stresses : o. - l. 6- = r..A'"A
Defomation:
A. =L-L, (along), Ao =b-b, (cross),
ta, +4.
e.=-i, e"=
b
.
Poisson's ratio: u=litl
L€. I
6
nooKes law 6=t€- €=-:.F,
o. P uo- uP-
a, =€, L=-L=-L. A^ =c^b=-b:-b.EEAEEA
Temperature
b)
-. *ato
Case a/
^ 0.at'EA A, L,
Keacrron:
^-O*L!. "=i.
k=--.
n
Axial force N =-R (compression),
-Rcr'AtoERo.atoE
A, lrl-k'"' nA k(n-l)+l
n
For A, =d, i o=6.r =62 =-61.4t08, lt'=4-lj
Where T"0 md T"0 re original and considered temperatures.
0 = coefficient of linear expansion
Ato > 0 tension stress. At0 < 0 compression srress.
Case b/
Deformation: Ai = a.At"L

Tables 1.2 and 1.3a
Example. Bending
civen. Shape W 14x30, L=6m
Area A=8.85in'? =8.85x2.54'? =57.097cm2
Depth h=13.84in=13.84x2.54=35.154cm
Web thickness d = 0.27jrn = 0.27 0 x 2.54 = 0.686cm
Flange width b=6.730in=6.730x2.54=1'7.094cm
Flange thickness t=0.385in =0.385x2.54=0.978cm
lvloment of inertia I. = 29 hn' = 29 x 2.5 4' -- l2l 1 2 -3cm"
Section modulus S= 42.0inr =42.0x2.541 =688.26cm1
Weight of the beam ro = 30Lb /ft = 30x 4.448 I 0.3048 = 437.8 N /m = 0.4378 kN / m
Load P=80kN
Allowable stress (assumed) [o] = 196.2 MPa, [r] = 58.9 MPa
Required. Compute: o.,"* and x."*
..rT 2 DT
Solution. M = A+l:
84
-, (DL P
22
_ 0.4378x 6,
+
80x6
= 12 1.97 kN .m
84
0 4378'6
*
8o
= 4t.3t kN
o.,o, _ tvt _ 121.97x100(kN.cm)
s 688.26(cmr)
22
17.72 kN/cm': =177215.0 kN/m'?=177.215 MPa< 196.2MPa
I .1t90 kN/crn' - llJ900 kN/m' = 18.9 MPa < 58.9 MPa
STRESS and STRATN
BENDING 1.2
".. lt I
rr-q;r_
%l^I
T---_]______T t
--T;Z'u* =?
Moment diogrom
*-------= v=f
Sheor diogrom
"!4,.
Stresses ?f----r:
in''ti"o-ii-.n"ion" 9rj I ll-e
zi.zll ljra,
-11""
F---iq-E;Fiq-- I
lsvl
t!-^tfg{^-L,| ,A1,sv I
lzl
#
u L ue0d am fd
E+ h l+E ffi,€
E E A-E.E_'E
I -g4gLBH PtrE
BEIEEEE
RH=EEItr
""€ F*R I e-,8
Stress diogroms
4
bcndtngslfcss; o--.)
I
^. VS
Jnetrstress: T=-
l.b
Stresses in x-y plane:
oy = 0, o" = 6, 1., ='tv ='c
Principal stresses:
o l/ .
o'^. -:l r/o'4r':
Maxjmum shear (min) stresses:
l/'_
r,,"" =t;Vo,'+4r'
il/
The principal stresses and maximum (min)
shear stresses lie at 45' to each othcr.
Stress diagrams
o-diagram:
"" =*T, "".=0, ",,=-{
t-tliagram: {", =0, ri" =#=#, "",
=t
o,""" -diagram:
q =*+, o", =+r=+!I, o,, =o
o,.," -diagram:
^3VM6..,U,6 _-T=--" O ___
24 S
T,,,, -diagram:
oM3Vi =I - t-=r-. T _rt-+_
22S2A
t,",,, -diagram:
oM3Vt. -T j r- - t-- -22S2A
Note;
"+ "- Tension
"- "- Compression
:-

STRESS and STRATN
VS
ess: T=-
I,b
h ) b/h'z .)
;+Y l=;l ;-Y' I'z / L+ )
"'J') 6v(t' ,)
bh'14 ')
0, for y=9; x=
v. /h t)
'r,d 2 2)
./ h ''lol
t-'l I
)l-l
l
ear str(
(h )rl
l;-Yll ;
b(h'
i[7-'-thr.
_.b
t2
,h
2
lr =0,
fh r)
lt-t)'
fh r),
lt-t)-
She
. =!(_y
zl
b/ Tl
-i-bt I
r,b I
tl
Iiu,[
r,dl
I
al
f
Case
Bending moments.
tvomentduetoforce e' V=nln4 + nt',
M.=Mcoscr, Mr=Msino,
[l!l = r,-or
LM.]
For case shown: M, = PyLcos d, M, = {Lsin o,
M=PL
o-r MIY'9'0
'f=-s I
r"lr)Stress:
- ,M( s- )
""",
=.
tl
cosq+ fsindJ
Neutral axis: tanB=Ia1uno.
ly
Deflection in direction of forc" f
'
A = UI{ +{,
E^. ^--^ -L^...-. ^
P,L' P' L'
For case shown: L. = :!L. A =
') -
' 3Et.. lEr
BENDING
n two directions
==-

STRESS and STRATN
COMBINATION OF COMpRESSTON (TENStON) and BENDTNG 1.4
uompressron (Tension) and bending
stresses: o=* t Yt tYr,A I, I""
PM,M6=_t:+-';lJ A - s, - s,'
M,=P e", M,=P e,
hb' b.h, ^ h.b, ^ b.h,
= 12' ''=-r'
t,=
6 ' t'=
n
i' i'
Neutral axis: y,,=lz, z"=!.
"Y "r'
i,= Jr) A, i" =r/i7a, a=u.rr
]-i f t +)
-lil {l ll lt
'+ + {+ffi
Euler's formula:
^ n'EI liP.= ,= for 1..,,)n,/^:..
(kr)' v R.
where R" is the elastic buckling strength.
. kL -1r1., -ilj1. stress: o.^ Saj.
Axial compression (tension) and benl
x
| ,
^{lb
Stresses:
compression o.," =
tension o.*
where : Mo and Ao: max. moment and
ma. deflection due to transverse loading
NMoNa,,
A-q'tJ
P"
NM"NA^
A S, S. , N'
P.
-9-

Table 1.5
Example, Torsion
civen. cantilever beam, L = 1.5m, for profile see Table 1 5c
h=70cm, h, =30cm, h, =60cm, h, =40cm, br =4'5cm, bz=2'5cm, br =5 5cm
Material: Steel, G=800kN/cm'? =8000 (MPa)
Torsion moment M, = 40 kN 'm
Required. Compute '[* and q"
h1n
Sofurion. !=i::=O.Ol . 10. cr =2.012,
br 4.)
lt=9=z+r 10, !-=4= 7.27 <10, c,=z.zr2
b2 2,5 br 5.5
1,, = c,$l = 2.91274.5a = 825.04 cma, I'. = c,6l = 2 212v 5'5a = 2024'12 cma
h hr 6ov? 5l
I, =",.', ="":" =312.5cma, lI,=t,, +t,,+I,.=3161.66cm4
t, =,
t' =tt9tjuu =574 85 cml'.h5.5
40x{100)
t.- = IY1L1II1= 6.958 kN/cm'? = 69580 kN/m'? = 69.58 MPa
.no _ 180. M,L _ 180 .40x(100)x1.5x(100) - 13.60
* n Gl, 3.14 800x3161.66
STRESS and STRAIN
roRStoN lr.s
o/.
b/.
r,,
ll-T-r
'* .'klo
[dJ"
lLnox
,-=.f g
Eot
I=rD
Bar of circular cross-section
Stress: , =M'.9=M,I ) q'-p-"n
, fido ^ rdlIo=-=.9.16'. So=-:" =0.2d'.
Angle of twisr: eo -
180". M L.
n Clo
Where G = Shear modulus of etasticity
Bar of rectangular cross-section
Str.rl t*^l{'. Angleolrwist: ,o-
1800.M'L.
s,ncl
rr h->ro:
,=T. r =i=T
tr !<to: I, -c .b'. S, -c,.b,.t)
ln point l: tr =T.u", inpoint 2: ,c2=c1.,t^,,.
t, /h -
a,
c2
cl
1.0 l.J 2.0 3.0 4.0 6.0 8.0 10.0 For
h/b>10
0. r40 0.294 0.457 0.790 123 L789 2.4s6 3.t23
0.208 0.346 0.493 0.80 1.150 1.789 2.4s6 3.123
1.000 0.859 o.795 0.75 0.'745 0.'743 0.742 0.742 0.740
c/. F_h-
r=ts-F--t-{
l"-tir*r
-l ; '+l- *l
l.aH;#-TTE]
'F-i-
fl"
". [J''
=
EFi rndt
Profile consisting of
re cta n g u I a r c ro s s - s e c t i o n s
i=n
Ceometricproperties: ,-I' . g =-l' . n=3
Assumed: .t0, lrrto b.;;
Dr b: b3
b,>b, , b, >b, (i.e. b, =b,""")
t,, -crbi . I =
h,bl
r,. =c,b1 .
I, =Ir, +I,, +I,,, S. =
I,
.
' b,'
Stress: t,,. =!!r linpoint t.1.
sr
Argle of twist: go -
180'
'
M'L.
rc GI,

C u rved bea m (lransverse bending )
C u rve d bea m (axialforce and
STRESS and STRAIN
CURVED BEAMS
oI
Stresses:
- M y-R,,
" _leo. =-.-, h"_
' A.c y "
tA'
c=R_Ro
hl
lf :<0.5. c=--j! forallcross-secrionlypes.
R A.R
For case shown:
A =Ar +Ar,
M R._R"
'A.c R,
"+o " - Tension
"*o '' -Compression
^. N. M o-R"SreSSCS : O^ =
-+ -'AA.cRo
Forcaseshown: c=R-Ro,
N=P, M=2PR,
_ P zPR R, -Ro
-' bh bhc R"
_ P ,2PR R"-Rb
" bh bhc Rb
Note. For beams with circular cross-section:
,( | r) f '.,''rn.--ln+,/n'-a I o' no=nlr-'l*l .
z r *., L l6R/]
d = diameter of cross-section.

STRESS and STRAIN
.b'
dh
"tl
3NE'l6n
'qae
[i .6 xo
9^ll
8 =!'
E.9
",q'0 h.H;iEA
.E6tl
X ^e+N
"9,. .6
oP
E=
r
,tvt
c
nl
d
o
6
o
o
o
Tabl,e 'l
"7
Example. Continuous deep beam
Given. Beam L=3.0m, h=2.0m, c=0.3m, thicklessb=0'3m, w=200kN/m
Required. compute Z, D, d, do and d.,,* forcenterofspanandsupport
Solution. Atcenterof span:
Z =D = a.xljwL= 0.186x0.5x200x3 0 = 55.8 kN
d= oo x0.5L=0.888x0.5x3.0=133 m
d0 = cdo x0 5L = 0 124x0 5x3'0 = 0 19 m
o.* = ct. x w / b = 1 065x200 I 0.3 = 7 I 0 kN/m'] = 0 71 MPa (tension)
At center of support:
Z = D = cr, x0.5wL = 0.428x0.5x200x3.0 = 128 4 kN
d = aa x0.5L = 0.656x0.5x3.0 = 0-9tt4 m
do = 0(a. x 0.5L = 0.036x0.5x 3.0 = 0 05 m
o,."- = ctd x w / b = -9.065 x 200 / 0.3 = -6043.3 kN/m'? = -6'04 MPa (compression)
0
I
{
[,
m
UJ
U
a
o
t
ts
t
o
(J

Tables 1.8-1.1 2 consider computation methods for elastic systems only
STRESS and STRAIN
DYNAMICS, TRANSVERSE OSCILLATIONS OF THE BEAMS 1.8
NATURAL OSCTLLATIONS OF SYSTEMS
WITH ONE DEGREE FREEDOM
1 SIMPLE BEAM WITH ONE POINT MASS
Dettections
N
1 Y
r-
ffid;1,;lt-+FORCES:
l'-Weight oftheload, M"""' .=3
g
( ^^.cml!-cravitationalacceleration.l g=981 ;
sec'/
11 - Force of inertia, P, = T ma
il = acceleration
For shown beam:
Maximum Bending l,4oment
.. a.b M
M.- =(Pr q).-, Stress: o= jje.t
I I,
DEFLECTIONS:
A.r =Static deflection due to Load p
aA =Max., min. deflection due to Force P
A,t(r) = Static deflection due to Force P = 1
c=amplitude, c=1Ai
MaximumShearfor a>b
V =/P+P '1
stress: t=* S
.t
v
l)eflectionsN
I
-rz!-
ffi*^| --1---- |
i-t--*-f-.
Forceofinertia: C=4+
lvlaximum Bendins Moment: Mh"* =[tP-t,) ;
Maximum sheari
"-
=;[ry.t)
Deflections- I
=- ----'r,
1__?| , ---l
?eFI
Forceofinertia: P, =7
Maximum Bendins Moment: Mnu =(+.t] t
Maximum shear: v,"- =
3"#I'*r

STRESS and STRAIN
DYNAMICS, TRANSVERSE OSCILLATIONS OF THE BEAMS
DIAGRAM OF CONTINUOUS OSCILLATTONS
Equation of free continuous oscillations: y = csin (rot + <po
)
Where: ou =initial phase of oscitlation, O" = -..in[&]
c,/
c0=amplitude, t=time, T= periodoffreeoscillarron, l=4=ZnN-
Ie
o = frequency of natural oscillation, . =
E
DIAGRAM OF DAMPED OSCILLATIONS
Equation of free damped oscillations: y = coe
*t,' . sin ( rot + <po
)
F-----'-=-
co =initial amptitude of osciilafion " - /,,r *f vo + yok 2m )'
' *-!r,-l , .j
Q0 =initial phaseof oscillation, Qo =rcsinl & l, t. =initiat deflection
co,/
v0 =beginner velocity of mass, e =logarithmic base, e = 2.7 1828
k = coetficient set according to material, mass and rigidity
T = period of free oscillations, T =2ja I 0t
-
o = frequency of free oscillation, ro= a/r/ rn- [k/ 2m]', For simpte beam

STRESS and STRAIN
DEFLECTIONS:
A,* -A*(p) +A$G) +Ai
Aq(p) =Static deflection due to Load P
A,r(,) = Static deflection due to Force S
Ai =Static deflection due to Pi ,
Ar = Pi .A*(rl
DYNAMICS, TRANSVERSE OSCILLATIONS OF THE BEAMS
FORCED OSCILLATIONS OF THE BEAMS
WITH ONE DEGREE FREEDOM
SIMPLE BEAM WITH ONE POINT MASS
qY
TORCES:
l' -weishtoftheload. tvtass, m=1. [*=oS'li 1
g sec-)
S(t) =vibrating force, Assumed: S(t)=5q.rt
ll =Forceof inertia, q =A'1'-A-5"o.11' Astr
rp-Frequency of force S(t)
A.,t
) = Static deflection due to Load P = I
Equationof forcedoscillations: y=c e-'' " ,in1rt*,po1+-ffQ .or,pt
c. e-t' " sin (ot + g0) =free oscittation. :jj!]]- costpt
f((D'-a-J
e0 = beginner phase of oscillation, ,1, = *..i" f
bl , y0 = beginner deflection
co.i
co=amplitudeof freeoscillation, co =c, c=amplitudeof forcedoscillation, c=ko.A.,,.,
:k = coefficient set according to material, mass and rigidity
o = frequency of natural oscillation, T = period of oscillations, T = 2n / or
kn =dynamiccoefficient. k" =#
./f'-ql'*[k q,l'
il rUJ') Lm (o"l
lf k = 0 (damped oscillation is not included 1: ko = -_L
,vt-tt
e=logarithmicbase, e=2.77828 /e=sgf
"t ). g=gravitational acceleration.
[_ sec_/
forced oscillation

Table 1.11 Dynamics, impact
Example. Bending
Given. Beam W12x65, Steel, L=3.0m,
Momentof inertia I.=533in4x2.54o =22185 cm*
Section modulus S = 87.9 in3 =87 -9x2.543 =1440 4 cmt
lvf odul us of elasticity E = 29000 kip / in: -
29000-!j8222
= 20 1 47.6 kN/cm']
' 2.54'
Weight of beam (concentrated load):
W = 65 Lblftx3.0 = 195x4.448/0.3048=2845.1 N = 2.8457 kN
Load P=20kN, h=5cm
Required, Compute dynamic stress o
sorution. A. -
PL'
-
20x(l' 100) - =0.025 cm
" 48E1, 48x 20147.6' 22 I 85
Pr lo ' I ,20.4 - loo kN .mBendingmoment V,,-
O:
ku-
O
51r"". o=Y.= 306*100
=21.24 kN/cm'? =212400kN/m'=212.4 MPa
s 1440.4
Table 1.11 Dynamics, impact
Example. Crane cable
civen- Load P=40kN, velocity o=5m/sec
cable: diameter tl=5.0cm. A=19.625 cm', L=30m,
Modutus of etasticity [r = 29000 krp/ iDr = ?249rji922? = 20147.6 kN/cm'?
2.54'
Computedynamicstress o forsudden deadstopRequired.
Solution,
4",
Stress:
PL 40x3(r(l0lr)
- t,.-{t,) cm, k - -j- =
EA 20t47.6y 1q.625 Jg 1'
o=
P
(i*k^)= 40 (l+2.9=7.g49kN/cm'? =79490kN/m'? =79.45 MPa
A ' 19.625 '
STRESS and STRAIN
DYNAMICS. IMPACT
Elastic design
Axial compression
Bending
Crane cable
tt
It
- ff-r
t= strking velocity, , ='Dgt
g: earth's acceleration, g =9.81 m/sec'?
A*= deflection resulting from static load P
W= weight of the structure
B: coef'ficient for miform mass
PL^Itsor snown @lumn:
",
= go . p =
J
P
lr)mamrc stress: o=-;.KD.
For shown beam: a' =
Pt'
B=11
" 48EI,
.
35
Dynamic bending moment: MD =I! k .
P
Dlmamic shear: Vu =
t
ko .
For stresses see Table 1.3
Sudden dead stop when the load P is going down.
Dynamic coefficient:
,UKD =-1==_- ,
vg
^",
whete: o: descent's velocity,
PI
EA.
Maximum stress in the cable:
p
6=_(t+ko)
A
A = area ofcable cross-section

STRESS and STRAIN
DYNAMICS. IMPACT
Elastic design
column buf f er spring
Motor mounted on the beam
tt
T-iA
motor's weight,
- centrifugal force causing vertical
vibration of the beam, 4 = mq'?l
rn : mass of rotative motor part ,
r : radius ofrotation ,
n : revolutions per minute.
Cylindrical helical spring:
D = average diameter
d = spring wire's diameter
n : number of effective rings
G: Sheu modulus ofelasticity for spring wire
Dlnamic coefficient:
p
Dlmamicstress: o=- : .k,, (compression)
'A
E= Modulus ofelasticiry for colum
A= rea ofcolum cross-section
D)namic coefficient: kD -
-'r-4',o)t
s-frequenclof force l. -=# t^=#
[;,)
o)- beam's hee vibration tiequency. t=,E [ ' I- Y PA secl
A = bem's deflection by force P = I at the point
of motor attachment,
(- Ij )
I lorshowncase: A=- l.
| 48EI,J
_ JOo
Kesonance: Q=O, n=r.
lt
Stresses:
PL F.K,,L
blallc slress: o=-" uwamlc stress: o--.
45, ' 45,
2"=f {r+rr")

NOTES
q PFIOPHFITIES
OF
GEONIETFTIC
SECTIONS

PROPERTIES OF GEOMETRIC SECTIONS
for TENSION, COMPRESSION, and BENDING STRUCTURES 2.1
I
r-T--?--.r
{ l.t l-"
'tfr-*'
1. SQUARE
^4 ^1
A-ar. t,=t"-i- t,=1
r.= t - ? ,.= ,, - ,fu.=
o.zr ,^ , ,=
+
ffi*
2. SOUARE
Ais of moments on diagonal
^ ^2 L-^ l;, t tt^
4l
A- a-. h= avl- t.42a. L,= l, - ;:. S.= S. _ *:== 0. I l8ar
L2 6J2
."=. = -!- o.:tsa. z- -3-=o.zlea
./r2 3J2
ll x,
rtTY
-l],I'd(l-"
*
'[ *'l' .'
3. RECTANGLE
, bh' bjh bhr brh
^12'12"3',|
hh2 h2h
S -;. S -;. r,-0.28ch. r,= 0.289b.
b6
d'sina
48
ry'
4. RECTANGLE
Axis ofmoments on any line through centerof gravity
I
A= bh. y, - y"- -1h cosa - b sina).
2'
hh _ bh (h?cos':a t b) sin2 a)I, - ,; (h'cos'a'b'sin'a). S
-
tz " 6(hcosa+bsina)
., " o.zso6'"oJ* btin'al
r-T+1I T--]lr-
11- _'--
--[il
A= ah + b(H - h),
t,:
$. fe' -o'r, r,=
* *$o-nr,
s.:
Su'-r"r* #, r,=
* *
frr-nr
rlY
t"i--| lT---T'-'-'1---:-T
tffi|
6. NONSYMI,IETRICAL SHAPE
A=bc, +a(ho +h,)+Bco, b,=b -a, B,:B-a,
aH']+ B,c,+ b,c.(2H - c. )
2(aH + Brcb+ brc,) ' rt " Jh '
t_
I, - ;(By; - B,hl+ ur' - o,nr,
J
-29

for TENSION, COMPRESSION, and BENDING STRUCTURES 2.2
7. ANGLE with equal legs
. h2+htt[t hrr-2cA- t(rn - t)' y -
2(2h - t)cos4f ' t'=
-E-'
t"= llzc'-z1c-tY *tq'-2.* ]ty''l- 3L 2')
c= y,cos45"
",'"lf'r'"nt
h2+hr
A= (b _ h,)_ r(h _ b r. x,_ - "r' . v._ jj______:!-.
2(b h,) -" 2(h I b,)
lr
r^= -lrlr'-y,l tyj -u,(v, -r)'].
lr
t,- lfr1U-xo]'-trx] -tr,1xo -t;']
l, = I.* md I, = 1.,". tun:po = J!' .
l*y= Producr ol inertia abour aes. bb hh L
(moy. r{) =.4(b*hJ,
lt)l
A =-bh , rro =Jh . 1 =:rr. d =1(b, -b. ) .
, bh' , bhr , bhr
-" J6'' t2' 4'
, hb(b,-b,b.) rr(uj+ul)
"= J6
"
= 12 '
hh2 hh) h
S",0, =:-(forbase). S,,,, =
;(lorpointA).
r" =#=0.236h
10. RECTANGULAR TRIANGLE
^ bh cL , bhr hb'
221636
, b'h' Lc3
-v' 361: 36'
or: Ir, = I"cos2a + I*sin2a + 2I*rsina cosa,
.bhbrht
sln,r= -, cosa= -. | = --L' L' " 72'
h
r-= _:+= 0.236h.' 3^12

PROPERTIES OF GEOMETRIG SECTIONS
for TENSION. COMPRESSION. and BENDING STRUCTURES 2.3
x,
x
xt
n=jtu+u"',':=$f: ,=ffin.
, _h'(b;+4b"b.+b:) , _h,(b"+3b,)
'" = 3o(b,'bJ "'= , '
'*,
=n'('llno'), s"" =I'luotto-), s*, =L(.p),
r'161r,*+up3ay
6(bo +b, )
"ry
12. REGULAR HEXAGON
A = 2.598R'? = 0.866d', I. = Iy = 0.54lRa = 0.06da,
s" = 0.625Rr, S, = 0.541R"
r_= r,= 0.456R= 0.263d.
J-Z--h"r7-"
I
13. REGULAR OCTAGON
A= 0.828d?, I. = Iy = 0.638R4 = 0.0547d4,
S, = Sy = 0.690R,- 0.l0q5dr. r, = r, = 0.257d.
@I
14. REGULAR POLYGON wilh n sides
.ltd^a^a360'
A-_na-col-. K=- K__- d=_.
4 2 2sin4 2tan! n
22
r. = r. -
nuR'{r2R
*u')= {{tzni+a'l= A{6R'+a'l
" 96 ' 48' 24'
a= 2J(R'-Ri)
-ffi'
33

for TENSION. COMPRESSION. and BENDING STRUCTURES 2.4
I
,/F,-l-'l-;" F l-x
H/I t-dJ I
l----.0--l
16. HOLLOWCIRCLE
*n7 / -n4
n="" (r-E'). E=i. r=r ="" ft_8")
4 'D 64'
u l, .)
5 =5 =_{l*C t. r =r =_.il_r-' ) l1 J I y
'
! >'q
nl
-dJL=-.
6
g-
17. TH|N R|NG (t<<D)
-hl+
A= rDr, t, = 'il ' . 0.3926D'r,
8
S,=
?= 0.7853D']r. r"= 0.351D.
,-l-Tts i - l-{r,I o-zn -l
I
18. Half of a CIRCLE
A= n7
- o.zszo', y6= 0.2122D, y, = 0.2878D,
I- = 0.00686Da, I, = I" = d= O.OrrOo,
s., = o.xtz(!)' -ror bottom, s", = o.rsor[!)' -ro. top.
--'K{
m-Ti
rQz dR
e- |= 0.785R'. y, = #=0.a2an.
y = 0.s76R.
I" = 0.07135R4, I, = 0.03843R"
r" = r, = 0.0548eR'. r,,= r, = f= o.'ru.,r*'
7..-.--- -,^FHl
. 20. Segment of a CIRCLE
nno
= eg b=2Rsina, s= 2Ra,d=
ffi, t!= 2a-sin2a. k= J(p
o = {E. y" =rR. r^ =4t' , J*cosa). 1 =-p{1r-r.ora;.2 '" ^ 8 ' 8 '
(d - in radians measue, a- in degrees).
-35-

for TENSION, COMPRESSION, and BENDTNG STRUCTURES 2.5
I
|-7z'i-
'l lt{Tr-*l;.1
21. ELLIPSE
, lt , zab' Ab' ratb Aa2
A= -aD. I = _=_
46416'6416
- rabt Ab ^ ra'b Aa
).= _= _. 5 =' 32 8 " 32 8'
ba
''
4' r 4
I
|ffir..
11+#42-"
t*t
22. HOLLOW ELLIPS
t= |@a-u,a,),
r. = fr(uu'*u,ri), t, =
ff(u'a-uia,),
s.=
fi-("u'-u,ui), s"=
fr(u'r-uiu,)
I il.l,--:-Ta
-Fl-E[-"
t-*? j
23. Segment of a PARABOLA
^ 4ab 3a 4ab' ab'
;- = -.J f t) )
, I oa'b l2Aa'z , 4a'b 3Aa2
't75t75"71
, 32a3b 8Aa2
" 105 3s
v
-tr6ffi4"
l*i I
24. STEEL WAVES from parabotic arches
r= !tea+s.zt), b, = jtr*r.ut),
u, = ]{u-z.ot), r', =}{r'*,),
r',= j{n-t), r.=
ff(ur'i-u,r,l), r"=
o4
W
25. STEEL WAVES from circulararches
A=(irb+2h)t, hr = h-b,
. (zb' .,. rbh'zt.,lr. -I-Tu IrT-T-il! tr..
t 8 4 6')
^ 2r.
h+t

2.6
Cross.section Moment
of inertia (It)
Elastic section
modulus (S,)
Position of xd",
(r."" = M, /s, )
^ nd'
-' tc,
At all points ofthe perimeter
@ r,=+ (dl-di)=r, ^ t[ d.-d
"' 16 d,
At all points ofthe
outside perimeter
ry I. = 0.1 154 d" S, = 0.1888 d3 h the middle ofthe sides
"@ l. =0.1075 da S, =0.1850 dr In the middle ofthe sides
l, =0.1404 a S, = 0.208 a In the middle ofthe sides
ffi h tbl -bi )
'' - 14b-bJ -
- 0.21 bl
^r."' u,
in the middle ofthe long side
e
"Flrl-
H
W ShaDe Angle Channel Structtral Tee
-lhkj I
l=n.F""' S=''-rh
L I T
n=3, =1.2 n=2, n=1.0 t2 n=2, I=1.15

NOTES
3. BBAI{S
Diagrams and Formulas
f o r
Various Loading Conditions

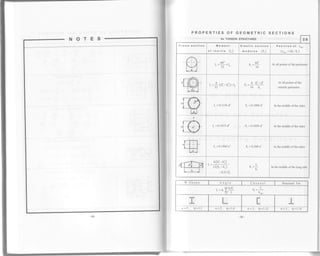
The formulas provided in Tables 3.1 to 3 1o-for determination of support reactions (R)'
bending moments (lV), and shears (V)*are to be used for elastic beams with constant
or variable cross-sections
Theformu|asfordeterminationofdef|ectionandanglesofdef|ectioncanon|ybeused
for elastic beams with constant cross-sedlons
SIMPLE BEAMS 3.1
-fti=Jl]fi:o No,"*u=*.,n=*,
q md 0b in radians
LOAOINGS SUPPORT
REACTIONS
BENDING MOMENT DEFLECTION ANG LE
OF DEFLECTION
r-i--F-irt___L_{1' Lr 4B-
t Mofnent
lqryl; Sheor ''M-o I
tr%rd'r
P
R_ =:"2
D
D -''2
PI
at point of load
pTl
-* - 48Er
at point of load
pr2
r1 = 19 =-:aI 6EI
b.aL
Momerlt
*qIPl
Sheor l'u.o"l
h
D _D "
"I-
o -o
o
.I,
'* ='+
at point of load
^
Pa2b2
3EI. L
at point of load
I
Dr2
6g1 >t >t /
Dr2
6EI'- -
',
a,b
L' '' I,
I luo-entl ,
ir@i1,,,1 st'"o. j'"'j
''-v
qJ2
D *D _D M.* =Pa
between loads
Pabt -4a'_
24F.1
at center
L*a
2E1
tfr*r-Fl
-r-J+'_l+
Morient I
ro4Pi';heor
|
Mfrf I
|H , r
'2
1p
"2
DT
z
at center
^ PIJ
20.22Er
at center
pr2
24EI
v,lilffi"'*i

Table 3.2
Example, Computation of beam
civen. Simple beam W14x145, L=10 m
Moment of inertia l=1710 ina x2'54a =71175'6 cma
Modurus of elasticitv E = 29000 kip/in': -
29009:1!8222
= 201 47 6 kN/cm'?
Uniform distribution load w =5 kN/m=0 05 kN/cm
Required" Compute V=R, M,*, A',., O=O"=Or
., , -
*L
-
5"lo -_25 onSofution. v =K= 2 =- 2
wr- 5xlo'?
M jjji-= =62.5kN m
88
n -
5.*t'= s 005x(1000)"
=0.45cm=4.5mm
^'*-:94 gI 384 2ol4'7'6x71175'6
*= til
=
o ott(tooo),.t
t =1 45x10
rradim
" - zqql 24x20147.6x71175 6
I Momenr I
iwiln*l I Sheor I
'----VIrlIIIEnv2
SIMPLE BEAMS 3.2
LOADINGS SUPPORT
REACTIONS
BENDING MOMENT DEFLECTION ANGLE
OF DEFLECTION
lllt,tomeftll
lruqtrry;I lshqor 'M;d | '
ruv2
Pn
"2
Pnp--
"2
4 5 6
^ PA 2n2 +l
' 48ET n
^ PA 2n'+1
Dr =-.-" 48EI n
M.* =
PL
^2
PL
1J38
DI
1-333
Pil
19r'4Er
PL,
15IF,J
P]j
t2.65Er
I Moment I
SqI[ruIIFlI srr"o. lu* |
|n]-'*i_ft",
^wL
"2
^wL"2
M
wt
at @nter
: t L-x I
2'
M-
^5wU
384 ET
at center
wx { Lt-2Lx' + xt )
/^" 24Fr
WU
24El
lMoment I
ffi| | Sheor I
o -wdrr rr
" 2'
^ wa"
" 2"
?a
M,"""
al
^ wa'tf. I ")U.. =
-l
l--C" 6Er l 2')
^ wa'L/- l-,
I Mo*nent i
w]N#u.
- wcb
"L
- wca
nr=
L
.. wabc/. c )
r l-
^r
I
L LL)
c{b-a)
2L
=l u(r*'ru'
L
c'L'l R
+-lx-
64b | 6Er
+).
aI x=a
R
"q-__ac
" 24EI
R
"-_'ba
" 24EI
fi =4a(L+b)-c'?

NOTES
SIMPLE BEAMS 3.3
LOADINGS SUPPORT
REACTIONS
OF DEFLECTION
@.|}, | +:-,-- L -l -wL
"6
-wL
"3
M-"" =
*?=0.064wli
9J3
wnen x=u.)//L
=nno65):
CI
when x = 0.519L
7wC
I Moment I
'wi! sh"o. t.ymol
llTtrrr.* I r
360 EI
8 wli
360 EI
-*--t-
ffiiI Moment I
iql][ryilshuo. u*, I
IITrrrx I
M =*I,,12
at @nter
I 2OEI
at center
) wL-
| 92FI
4rllffi
i iuo-"nt t'
rqIIUPi
l- .n"Ju'* I
- w(L-a)
*,=r5il
wL' wa'
86
at center
5 wl-o
D. =Dr =-.1,
24F,1
c *1 1Y2,tJar - r-29 Ts
384 EI
. _, 8",,16"0rr - r-- T-q
JZi
at cenler
i-;;. IiquuPlI Sheor Mmr I
llTh"*-;",
D _ 2wu +wb,
^"- 6 "
o _ w, +2w0,
'.b- 6
L
wa
o.2 o.4 0.6 0.8 1.0
^ ri (8w, + 7w" )
" 360Er
^ I-r(7w, +8w" l
u.=" 360EI
N/
l3
"09
1130 c% sff
wlf,
8"00
X
L
0.555 0.536 0.520 0.508 0.500
when x =0.500L4","" ={wa+ub)L-,
to x=o.5l9l
r',*l q,",
-*--t-t-rirrrfllnh#-l.tr,I | '7
I Moment I
iql][ryilshuo. u*, I
vrllTFn* ln
v,llTffi- lv2

NOTES
v |Trrrrrrrrrrrrrr
vllrrrrrrr | | | rr rrrrr1t2
SIMPLE BEAMS and BEAMS OVERHANGING ONE SUPPORT 3.4
LOADINGS
SUPPORT
REACTIONS
OF DEFLECTION
E.-l--"*;l
ffit
R"=+
Ro =-R"
M,,* =M,
when x=0
M.IJ
d."...._
I ).)vbl
when x =0.423L
, M^L,
I 6EI
when x = 0.5L
^ ML
-
" 3F.I
^ M"L
' 6EI
Ll I
r---__,__-__1
, Mombnt
ffisheor I
o --MuI,
R.-Mo, I,
M, =-M^3"L
M. =M^!' "t.
M,.abfa-b)
]EIL/
when x=a
^ M,,L ^
" 6EI-
" M"L.
" 6EI-
/h2
f,=1 3l :
/^2
t =1-31 : I
' L/
ffi
R=Pl"I,
*r=t+
Mr = -Pa
For overhang:
a=-{L+al
3EI'
Between supports:
PaI r
A..,.... - -0.0642-
--
EI
x = 0.577L
For overhang:
P (2aL + 3a')
r)= ' '
6EI
" PaL
" 6EI
" PaL
"n - 3EI
,,w
.&;#
F--l---T---
j Moment lruo I
l-.".nI jff,-
i
Sheor ... ,
"---,--F
- wa2
2t,
o,=*[".*)
"2
For overhang:
.-.^ l
a=
*" (4L+3a)
24F.1'
Between supports:
,-.-2r2
A .. =-0.0321
*" -
EI
x = 0.577L
For overhang:
^ wa-(a+Ll
6El
^ wa-L
" 12F.1
^ wa-L
- 6EI

NOTES CANTILEVER BEAMS 3.5
LOADINGS REACTION OF DEFLECTION
{at f roe end)
I Moment I
) lu6ot
mttrr"* i
I sh€or i
TIIIIIIIIIIIIn P
D -D M.* =-Pt
prl
3EI
pr:
r)=:-=
zEI
D _D M.* =-Pa
Dol
A =::-/rr -")--, '- " J
otl
^ Pa2
2Et
, Sheor
*'lilTtrrrr*!
R =wL ,,_=_Y ,WL
EI
^wu
6EI
R=
*L
2 o 3OEI 24EI

NOTES
BEAMS FIXED AT ONE END, SUPPORTED AT OTHER 3.6
LOADINGS SUPPORT REACTIONS BENDING MOMENTS
AilD DEFLECTION
It^ =-Ptl+ll . at fixed end
" 2L"
Mr = Rrb , at Point of load
. Pa':b':(la+4b)
A, = ' '. at Doint ofload' t2uEl
R"
5
8
?
8
Rb
M" = -: , at fixed end
U, =-L*f ar x=0.625L' I28
a-^.=
*t' atx=0.579L
185EI
19281' 2
R^ =?wr'5
R. =IwL" l0
rvl- = -- - aI flxec eno
lf
..,r 2
M. =
*" at x=0.553L' 33.6
4r9EI' --
,.,r 4
- 426.6Er' -' ' 2
I sh"o, i
Ra=
:. Mo
2L
^ lM-
" 2L
M" = -+ , at fixed end
. M"L, 2.
".* =tff. ar x=-L

NOTES BEAMS FIXED AT ONE END, SUPPORTED AT OTHER 3.7
LOADINGS SUPPORT REACTIONS BENDING MOMENT
IAT FIXED EtID)
R" _
3M. (L' -b')
T:
3Mo (f -b2)
--*TR=
M [ /h'?]
M"=+l l-ll , I i. when b<0577L
- L '"',1
M" =0, when b=0.577L
v =-!n[r 3f !]'.]. when b>0.5771
" 2l L/l
I Sheor
q rTITlTlTlTITlflTlT[m v2
^ 3EI
"L'
^ 3EI
"U
1FT
M =:="v
,:F4 t
"Illml| ,n"o, I
r'IIIIUIIIIIIUIIIIIIIvz
lFT
f,
- 3EI
1FT
M =--.-"t
., oc'.-
-
t--'------'+'
1l
I Moment I
I sh"o. I
Vr llMffiMfiffi vz
R ,3EI
I-2
^ ]EI
c
lFT
M =-:::
L

NOTES BEAMS FIXED AT BOTH ENDS 3.8
AND DEFLECTION
, o lPb.t
4-{-l b
Moment
MolN.-L---lllMu
t l'Mr I
' Shdr I
; Shepr I
vtffi |
P(3a+ blb:
P=L
LT
P/a + 3b)a'
R=-
t
Prhz p.2h
M =--*i M. =--*:"'t"L'
tp"2kl
M, =
-", " at point of load
'L'
pa'b'
A, =.- . at Domt ol load
' 3tiEI
uoN***Juo
...r 1
M^ =M, =-
*"
12
M, =: . at center
'24
wLo
A =-. at center
384EI
R"
7_
20
3,
20
Rb
na.=-*t'. M,=-*t'"20"30
u, =
*f at x=0.452L
' 46.6
'
A-..= *t' atx=0.475L
764ET
wlo L
a=_. at x=_
768EI 2
[4omqnt
wa(L-0.5a) M" -Mo
.,,-2
nr^ =-
*" (:-+E+t.sE')
" 6'
.-,^2
M, =-
*" (E-0.758')
J
't.
L L
*, _ wa'
*
Mu -Mo
"2LL

NOTES BEAMS FIXED AT BOTH ENDS 3.9
IAT FIXED ENDSI
M^ =tr,t, =-wcl13-E:124'
.c
l=1
u =rafr-!i)-"1(r-e,)4 2') 24'
at center
^ 6Mnab
r.r
- 6M^ab
r:
v"=$!{2"*u)
v, =p("-zu)
wh"n *=!: M"=0, Mo=-ry-q
yb
I Sheor I
vr lTlTfffffflltTlTfffmv2
. 12EI
'v
^ I2EI
"L'
6EI
a
6EI
"I:
ffi'I Moment I
^ 6EI
"L'
- 6EI
"v
4EI
L
)FI
Mn=a

NOTES CONTINUOUS BEAMS 3.10
Support Reaction (R), Shear (V), Bending Moment (M), Deflection (A)
^T T^, T*"
L_______L_L______J-_J
j Moment
Luo i
lw$e/iwwiI ''u' i iu, I
n46U;d".
R" =Vr =0.375wL
Rb =% +V3 = 1.250wL, V, =V, =0.625wL
R"=Vr=0.375wL
Mr = Mr = 0'070wf ,
at 0375L fromR" mdR.
Mo =* 0 125wli
A = 0.0052-Ji. in the middle of the spans
E,I
@
ffi'I Moment I tM'a . M- |
FuwMiryt, lutl i'MzlMi
nffi,.
R" =Y =0.400wL, Ro =% =0.400wL
Rb =R. =1.100wL, Vr+V, =0.600wL,
V: =Vr =0.500wf
Mr =Mr =0.080wf , at 0.400L fromR" andRo
Mr =0.025wf , Mo =M" =- 0.100wf
,-r 4
A*" =0.0069i-:-. ar 0.446L ftom R, and Ro
EI
n = O.OOOZS
#, in the middle of spans I and 3
EI
A = 0.00052+. in the middle of span 2
EI'
@
E , T* , T,*", T^o . 1^"
i lru, i.*" i,uo I
ffiI i*i i'u'iujt i"il i
lrLrtti;lu'Wu,
R" = R" = 0.393wL, Ro = Ro = 1.143wL,
R" = 0.928wL
V, =!' =0.393wf, V: =Vr =0.607wf,
V: = % = 0.536wI-, Vr = Vs = 0.46awf-.
Mt=M4=0.0772w1j, al 0.393L fromR" md R"
M, =Mr =0.0364wf , at 0.536L fromRo md Ro
Mo =Mo =- 0.1071wl'z, M. =- 0.0714wf
Mt=M4=0.0772wL?, at 0.393L fromR" and R"
o.* =O.oOosIf . at 0.440L from R, and R.

Table 3.1 1 is provided for computing bending moments at the supports of elastic continuous beams
with equal spans and flexural rigidity along the entire length.
The bending moments resulting from settlement of supports are summated with the bending moments
due to acting loads.
Table 3,11 Continuousbeams
Example. Settlement of beam support
Given. Threeequalspanscontinuousbeam W12x35, L=6.0m
Moment of inertia I,=285 ina x2'54a =11862 6 cmo
Modulus of elasticity E = 29000 uiv tin' =PW!!Y- =
Seftlement of support B: AB = 0.8 cm
Required. Compute bending moments M" and M.
EI - ,20147.6x11862.6 ^
sotution. M" =k"+ A, =3.6-" :" :i" -' x0.8=l9l2.0 kN'
" "v - (600)"
20147.6 kN/cm'?
cm=19.12kN m
M. = k.
?' ^"
= -2.+4ffi9!x0: = -r27 4 7 kN cm = -l2 ?5 kN' m
CONTINUOUS BEAMS
SETTLEMENT OF SUPPORT 3.11
Bending moment at support :
v =t% a, where k:coeffrcient,
v
A = settlement of support.
CONTINUOUS BEAM
Bendlng
momqnt
SUPPORT
A D E
COEFFICIENT K
IWO EOUAL SPANS
r4- r.500 3.000 -1.500
THREE EQUAL SPANS
at-
-1.600 1.600 -2.400 0.400
Mc= 0.400 -2.400 3.600 -1.600
FOUR EOUAL SPANS
rt- 1.607 3.643 -2.571 0.643 -0.107
Mc= 0.429 -2.57 | 4.286 -2.571 0.429
Mo= -0.107 0.643 1.571 3.643 -1.607
FIVE EQUAL SPANS
M"= -1.608 3.645 -2.583 0.688 -0.t72 0.029
Mc= 0.431 -2.584 4.335 *2.756 0.689 -0. I l5
Mo= -0.1 l5 0.689 -2.756 4.335 -2.584 0.431
Mr= 0.029 -0.172 0.688 -2.583 3.645 -r.608

NOTES
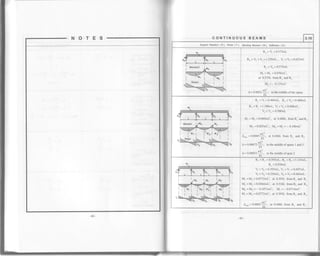
Table 3.12
Example. Movingconcentratedloads
Given. SimPle beam, L = 30 m
q=40kN, Pz=80kN, Pr=120kN, P+=100kN, P,=80tN' Ip, =+zOttN
a=4m, b=3 m, c=3m, d=2m
Required. Compute maximum bending moment and maximum end shear
Solution. Centerof gravityof loads (off load Pr):
Bending moment
I(p, .*,)lIq = (80x++t20xz +100x10+80x14)/ 420=32801420=7 '8 m
e=z.s-(3+4)=0.8 m, el2 = 0 4 m
R. =tp xr!-9lrl = +zo(rs-0.+)/30 = 204.4 kN
^ u, ) ))
M-* = Ro [l - :l-tt, t". b) +P,r]= zsa.47 (ls - 0.4) -[40x(4 + 3) +80x3] = 2464 2 kN m
z z) -
End shear
Load P1 passes offthe span and P2 moves overthe left support
nu. =
Il u
-r, =42014 -40=*roroL30
Load P, passesoffthespanand P3 movesovertheleftsupport
n., =
It o-o-
=42otl -80=-r8.,.,
30
For maximum end shear load P2 is placed over the left support
v^ = e, +[r, (r,-b)+r, (L-b-c)+P5 (L-b-c-d)]/ L
= 80+[120x (30 -3) + 100(30-3 - 3) +80(30-3 - 3 - 2)] /30
=80+7240130=326.7 kN
-64-
SIMPLE BEAMS
o
U
J
t
I&.
ul
,U
I
v,
J
u
F
E
x
UJ
u
t
o
(.)
(9
I
o
I
3.12
E.Ea?EsIl:=:;sE:68.fi; f i'riu - I oi E H H e
e H t ;1. 5 P F e
Ite ^l-qEgE:;; il
=
3 I t65 X r E: t E
E6; -< E F !
E;Eeiisg!3E I * *: f E e g
; ; E n -l i * ; H *o * F 9:l o n
; r T Ei,I, ; Z Z H F
!EHF+#==$ E
EeE F A i E 3
;aE3
^]e5leg 'o
=
E
xE B -e e * 3
Eb
=
E E i .e
", -g
9iu-;
'<:X=
c{F s
:^Xg
;to.;:.:odo
6:^ h
3 93 E
>gE6 do
FF 6 E.
on6c
6;
.!-.=-
q P ^-
olo.
=a.Ex
:3!6
FgEEP5E E
ie; s
EE: E
xxE!
Fft!o
F-.L
i p€ 3
S EE 3
o
o
=
o
E
o
o
E
o
=
_1
ll"rT-j
f
)
E
0
.9
c
E
o
_
--t

f(
,l-
,f
lno
l-r
/
{' Eo
-9
q
t_
65

BEAMS
NOTES
INFLUENCE LINES (EXAMPLES) 3.13
Rt-
RB
lrlr--F---;O ,
" _LL=nT1_*i=
Me =o(*xLxP
xlL 0.1 0.2 0.3 o.4 0.5
d, 0.086 0.144 0.1 78 0.1 92 0.'188
xlL 0.6 0.7 0.8 0.9 '1.0
CX 0.1 68 0.136 0.096 0.050 0.0
Me = 0" xLxP
xlL 0.1 0.2 0.3 o.4 0.5
(,r 0.081 0.128 o.'t47 0.144 0.125
xlL 0.6 0.7 0.8 0.9 1.0
C[x 0.096 0.063 0.032 0.009 0.0

NOTES
BEAMS
INFLUENCE LINES (EXAMPLES) 3.14

BEAMS 3.15
>
o
o
o
E
o
o
o
o
++
^l ^^
TI
I tt
il-
A^.. r ll
r{}
F:b.ts69
E
o
o
o
o
E
o
G
.A
q
^O
<:
<rE,v.!
'ib"ll s
gF*
.. ! H B
-E(nE
E9o.=
gE ILo{
NOTES
o
uJ
z
l
lu
o
z
uJ
J
lt
z
(9
=o
)
v,
lu
I
o
oazu
<J
-E_=-<ux
Iu
o-
I
o
z
o
I
U
o
E
o
I
9
F
F
0.
t
u

BEAMS
o
uJ
z
:
llJ
o
z
ul
f
J
r
=
=o
f
ut
U'
zu,
<urJ
Fq.
zzuJ<
*x
^ut
-
z
o
z
uI
o
q
o
z
o
;
F
0.
T
o
o
3.16
oi 0;
il ll
iItl
o-i ^1
oj- ^-illl
>ffT
,croo
6.E
ooqm
---. o
<q
+=eO
{5H'.BE
<il-
Y>-9
B,tr o
_-o
E -:El:f
E
:{5>o
lltl
f{<
;EI-E@
o-
EE3Eoo[6
o
c
J
c
o
o
E-
o
o
=
i k{_
EI-II
E
=l
"fl
F r.{
-73-

NOTES
4. FFIAI{ES
for
Various Static
Loading Gonditions

NOTES
FRAMES 4.1
i'l jp
F
+
Llr 'i
'ls! -
lr
,l= rl
ld>
-#ITE
tplfi+ f
i fl- j" l,,.1*9
+" ',^ ,,
-
A
H
Ll
l-{
tl
E
-fTITITITFI
;l
o
-r- a
F
+
la-
'^
1rl+
^ l1 E13
la dl.l lS
r,l+ -lY +
Elil .l
;i *tE " +
It ! I
il>ll
>ll
>
l'l N
!lr *
- Tlc lCts Tl+
T i(lr ^-l -
=
"i El- Jl
B €l- rl F
ll't .'-
. il d ^_l
* +" |
'l
Bil^i
d, l
:
}r>
.t >-
?E.E.I-v,l drf
-"-LT+EirlN*g-
lla
->
H
E
-f-FfTtTtTn
-77 -
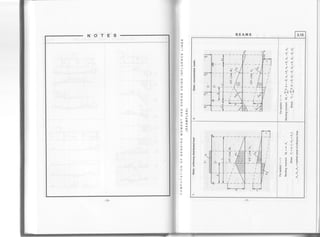
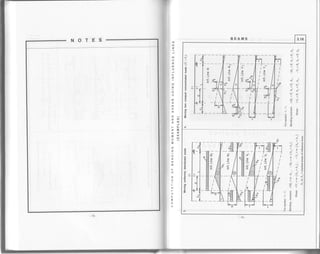
fhe formulas presented in Tables 4.1-4.5 are used for analysis of elastic frames and allow computation of
bending moments at corner sections of frame girde6 and posts. Bending moments at other sections of
frame girders and posts can be compuled using the formulas provided below'
For girders:
rr M">Md, rr,, =r3,,,-[Ytr-*1+rnr.]
tr M. <Md. rr,|,,-, =rri|!,- -[!cI4'*+v"]
lf M"=Mo=M., MeG) =M"t"t-M,
For posts:
M,(-) =M:(,) -(H t-M"or)
Where: M!,,, and Mf,-, represent, respectively, for frame girders and posts the bending
moments in the corresponding simple beam due to the acting load'
x is the distance from the section under consideration to corner c (for the girder)
andsupport aor b (foraPost).
o
z
o
=o
z
o
o
o
z
o
o
J
o
F-
F
o
o
f
o
a
o
o
J
=d,
o
lr
tt
o
U'
=
t
o
:o

Example. Analysis of frame
Given. Frame5inTable45, L=12m' h=3m
Posts W10x45, lr =248 ina x2'54a =10322 cma
Girder W14x82, lz=882inax2'54a =36712 cma
Load P=20kN, a=4m' b=8m
Required. Compute support reactions and bending moments
, I,h 36712x3 _n aRo F =
a
=1=0.::fsotution. K=iI=
t0322"n-w.uo'!
! L n
.. 3 pab _3 20x4x8 , =9.23kNn=, *tu.rt= z :rrz1o-sso*z)
- -' "
R _ Pb.l+6-28'z+6k
=13.57 kN
L 6k+l
Ro = P-R" = 20-13'5? = 6'43 kN
n, _
pab. 5k-l+28(k+2)
=7.8t3 kN.m
" 2L (k+2)(6k+1)
Mo =R"L+M" -Pb=13'5'1x12+7 8i3-20x8=10'653 kN m
M. =-Hh+M" =-923x3+7 8!3 =-19'877 kN m
Mo =-Hh+Mu =-923x3+10'653=-17'037 kN m
Bending moment at Point of load
n, =r"-[M.-Morr--a)+M".l. M:=+
r ' "l ' L
, _ =
roil;* _[
p.877
. -t'7.031 112-4) + r7.0371 = 34.40i kN. m
NOTES
o
z
o
io
z
o
o
o
z
o
o
J
IF
F
o
o
f
Iu
o
tt
J
l
-u
o
lr
o
o
-
t
(9
Io
FRAMES 4.2
l^
lo!
Elx,ltv
l=
-i^ ll
ll <-
E4
o.to f l'
!ll
E-
ll
all
t
',1' gl fls+l 5l
:- i+lJ ; fllN lle | *l
ol* ul d ll
dl+ il rr #l
ll *lr oa si,
-t ol
olN il Al
l* *l*
vl+ +l+
-lr !l!
l9 6la
-i-i9zrl llN T r
LIN 6l- *l I !
/,'E =":r," 1>
il ,l
a:E
-79-

FRAMES 4.3
I
^t
!l+
- lN +
'II T
gl E
i>
i
o
o
C
:6
F,i
d
+
;o
o
o
ul
i | >1, vi
flr qt= :ln =: ? ? g
;l-
=lJ
slr vl^ i ? Jrl or +l ,1.: s fgl ll 6l l-eE,;
>'l= f j ol#il il" j
-i.""tt.+>>r&
t
o
o
o
o
o
tl
lN
+l'j jl+
*lr rlJ l*Tl! ! | i-l
:--l o! |
Frt {l^ 3l^-. I -=l! dl-
<l- i?l =ldl* fil hl
il
tl]l " rl
r-til
+
o
t
o
o
a
NOTES
o
z
9
=a
z
o
o
o
z
o
o
J
o
;
F
o
at,
f
9
g.
o
o
J
f
=d
o
L
6
o
=
t
o
:o

FRAMES 4.4
tlrrr
.l< ^lE
ri 1-lle a{ <!-
;+
<
-t+ |
ll _1/
trtl
ET
'' EIH
> z--;-
- :ld
t+4 +,
'l :^ i I
@l@ €lN . -
| -t tl
qla
>"6
F
E. IN
ll Flo
llll
;('
I
p.l^
='
a
a
t4 | ^-l -| + {t =r>glK
;:<
-1-= L ?r6allo€
>
F
8
!
-la tl
". >
f
E -i--19 l-
a. lN
iltl
!c> I
o.l^ <"
a
a
olll
>15
;.--
.<a
tl:
*i >
il*t
aa
a"
-ITTTITITN tt
-83-
NOTES
-82-
o
a
o
:ct
a
o
U
o
7
et
{
o
?
ts
{|=
n
o
2
o
t
F
t,
{
I
I
I
g
tl
tr
H
5
l
{
E
It
{

FRAMES
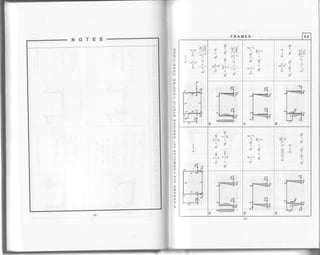
NOTES DIAGRAMS and FORMULAS for VARIOUS STATIC LOADTNG CONDTTTONS 4.5
M" =-+, ru,=*9
oo
Ph ph
M"=+ -, Mo=-]
oo
PB M"=-d! t,=*+
t"=.+, M. =-+
(+Ato)Steady
tr.t. =- fll'k . o.o,ot" h'(l+k)
lr^=-1r,,r.. k=I,h'2"I,L
d = coefficient of linear expansion
22 steady heat (+Ato)
M =
3E!
I'k*,')[I-*!)o at'" h'(l+k) 2/
M.=- ffl'k fr+L)a.at'" h'(l+k) 2 )
v , =-Iv.. y. =-$r[L]"a*' 2 h'2)
M, =-M-,, k=
I'h
I'L
Cx, = coefficient of linear expansion

NOTES
5. AFICfIES
f o r
Various Loading Gonditions

NOTES
THREE-HINGED ARCHES
SUPPORT REACTIONS, BENDING MOMENT ANd AXIAL FORCE 5.1
I v-diogro.
Vertical reactions:
IM" =RoL-P(L-x")=0, n^ =rf;
IMn =-nut,+Px, =0, Ru =PlL.
Horizontal reactions:
5-rrl. =n. !-s"i=0. H^ =R. !;4 ^2fLeft
Ix=Ha-HB=0, HB=HA=H.
Section k (x.,yo)
Bending moment: Mo = lM = Rox* -Hyu,
or Mk=Ml -Hvk '
/Shear: Vu =l R'^ -IP lcosQu -HsinQ*^l^al
Letl
or Vk =Vk'cos0k-HsinQu'
Axial force: *- =[*^ -lr]s;n4o + ucosq,
kftl
or Nk = Vk"sinQk +HcosQ*'
Ml and Vou = bending noment and shear in simple beam
for section x,
Tied
c IM" =RoL-p(L-x")=s, n^ =r!b;
IMo =-R"L+pxn =0, ft" =p.5-.
Horizontal reaction:
lx=-H" =0.
Force N, :
rrra- = n^ !-^-o-r[!-*"]=0.' l? )
1.ft
N" =][pf !--" )-r
r I
' dL 2 '
t^;j
I t,t^ =N,c-n"!=g. l.l, =P-
L
.
L "2dRishr
Tables 5.1-5.9 are provided for determining support reactions and bending moments in elaslic arches
wilh constant or variable cross-sections
Table 5.'l includes formulas for computing in any cross-soction k the axis force Nk and the shear
These formulas can also be applied in analysis of arches shown in Tables 5 2-5 9
Bending moment Mr = Re xr -Ha yo +Mo -IPr 'ar
Len
Axial force Nr = Ra sinQ+ Ha cosQ -lP, sinQ
Shear Vt =Racos0-Hermq-iq"otqhft
Where ai =distance from load P to point k

NOTES
Table 5.2
Example. Symmetrical three-hinged arch
Given. circulararch 2 inTable52' L=20q f=4m,
4f'+t 4x4'z+20'1
radius R=-=-l;;-=la.) m, x. =) m,
-(14.s-4)=3.11m
II
tanq. = | i-x. ltln-r+ y. ; = 1t0-5)/(14.s-4+3.1 1) = 6.367
r )
Q-=20.170, sinQ. =9.345' cosQ. =9'939
Distribution load w=2kN/m
Requirod. compute support reactions RA and Ho, support bending moment MA ,
bending moment M. , axial force N. and shea
I 1 wli ?.x2o2
sorution. n^ =iwl-=ixzx2O=15 kN , n^=;;=ffi =12'5 kN
e- =I-=a=o.zs, n- =J-=
3
ll=o.zrs
L20'"f4
M, =
#Ls(€. -Ei )- 28. -n. ] ='1?o' ;t{o.,t-o'2s'z )-2x0'25-0 778] = | r' I kN m
N. = Ro sinQ. + Ho cos Q. - w. x. sin Q, = 15x0.345+ 12.5x0.939 - 2x5x0.345 = 13.46 kN
V.=Rocos0._HosinQ.-w.x.cosQ.=15x0.939_|2'510.345_2x5x0.939=0.38kN
-90-
SYMMETRICAL THREE-HINGED ARCHES
OF ANY SHAPE
FORMULAS for VARIOUS STATIC LOADING CONDITIONS 5.2
A
+Ra
LOADING9
SUPPORT
REACTIONS
BENDING MOMENTS
Ro =R" =IL
*r^=""=*
wLl,ly E2 _ |
lvrm = g L+gm-!./-'tm..l
2
Ra =aw|,, Rs =:wL
s^ =H" =iF
', =
f t'te, -€'. )-26. -n.1
r- =S{16.-n-).
#5t
..f2 *f2
*^=-;. R"=
zL
H. =-lwf,^4
H" =f*f
-,12t r ^
t. =-?[8.-ir.+ni J
Mk =?(28,k-nk)'
4
,o lP o, ,
J{A B
*^ =r?, *" =t;
H^ =H" =P*
r',r^ =r;(zle,-n,)
rtlu =e|{26,* *ttu)'
-91 -

SYMMETRICAL THREE-HINGED ARCHES
OF ANY SHAPE
LOAbINGS SUPPORT
REACTIONS BENDING MOMENTS
w JIIIItrnn*
R, =:wL^ ai
'|
R- =:wL
---r2WL
n- =n^=-
48f
,.,r 2 _
u. =ft [:€. +s(8, -Ei. -8, +El )-'r.]
n- =*(zB*-n,).
wlllllnhn-, r R- =R^ =
*'
H^=n"=fr
v^ =ffPe^* a(si. -Ei. -e, * *) -n.1,
*^=-$, *"=$
H. =-awf"^12
Hu=l*t
r. =S1r{e,. -6i.)+n. -zq.]
r.=$ir€*-n*).
M- =Mol-

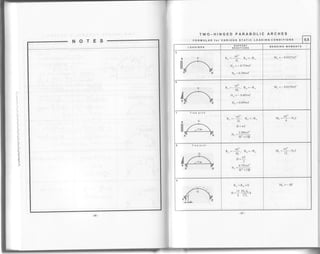
TWO_HINGED PARABOLIC ARCHES
sEToN
ll
ll
:ii
It
riii
ill
iiir
il
iil
iii
!ii
Table 5.4
Example. Two-hingedparabolicarch
civen. Parabolic arch 3 in Table 5.4
q 5
L=20m. l=3m. x=a=5m. E=i=--=O.ZS
4f(L-2x) 4x3(20-2v5)
-^,tano=-I_=--.tr-_".'
Q- =16.70, sinQ" =0287, cos0. =0958
Concentrated load P = 20 kN
Required. compute suppon reacrions Ro and H^, bending moments M" and M" '
axialforce N- and shear V" (atpointofload)
solution. n^ -PL,
u
=zo2?-
5=tsttl
20
. -
5P!u [r - rr, *E.l = :]4j l9
x r^fo.zs - z-o.zs) +0.25"] = 10.7s kN
f,A=-KL9-zr, >.1 g>l L
v =
PL
lae - :r (a
- ra, * q* 11 =
20I 20
f +ro.zs -:(o.zs - 2x0.251 + 0.2sa) =-e.s kN m]
8 L: -". - ' lt 8 L
4f (L-x)x _4x3(20- 5)xs
- r,_t=---F--'
M, =Roa-Hny. =l5x5-10.75x2 25 = 50 81 kN m
N. = Ra sin 0" + HA cosq- = 15x0 287 + l0'75x0 958 = 14 6 kN
=Re cosO. -Hosin0* =15x0'958-l0'75x0 287=I 1 3 kN
FORMULAS for VARIOUS STATIC LOADING CONDITIONS
5.4
Equation of parabola:
4ffL-x)x
l, = | ,coso*
' 't:
-.-- dy 4f(L-2x)
t-q=d* = L'
Coefficients: Forregulararch: t=0, k:l
t5 B | ^ Er_
Fortledarch: D=- ._. K=-. D= '
8 f'. l+1). E,A,
LOADINGS SUPPORT
REACTIONS BENDING MOI4ENTS
NMIIITIIIITITITTIIITIIIITIT! W n^=R"=*
Ho =Hu =
tt1
rr.r.=$tr-t)
15
8
B1k =-
f2' ^- l+r)
3l
R.=:wI_. R-= wL
^8"8
H- =H^=-K
l6f
M. ==(r-k).lo
tt 1
M- =l--:k lwl"'" 16 64 i
I
-q
R. =P" -" R-=P:.L"L
Ho =H"
5PL. r. ^". ".r
gf L' ' ')
rra- = IL[+e -sr. (E
- 2E' + E" ).1
' 8 L - ' ' t)
.L
4
RA
5wL - wL
24"24
= H. = 0.0228 "'" k
"f
HA
M" =Rof -Hof

TWO-HINGED PARABOLIC ARCHES
F'ORMULAS for VARIOUS $TATIC' LOADING CONDITlONS 505
LOADINGS
SUPPORT
REACttOI'tS BENDING I,|OMENTS
5
R^ =-;, R" =-Ra
Hr = - 0'714wf
Hs = 0'286wf
Ulc = - 0.0357wf'?
6
R^=-;, Ru=-R^
Hn =- 0'401wf
Hs = 0'099wf
M"=-0.0159wf'?
R^=-;, Ru=-Rn
H=wf
,, 2.286wf3
"' =Iii+r50-
u"=$-N,r
R,=-*' . R"=-R^
^6L
., wf
n=-
2
0.792wf1
"' =
fF +15F
..,f2
M" =rl--yr1
Ro =Ru:Q
-_ 15 EI.A, .
Ft=- -----X
8 f'L
Mc =- Hf

FIXED PARABOLIC ARCHES
Table 5.6
Example. Fixed Parabolic arch
Given. Fixed parabolic arch 2 in Table 5 6
L=20m, f =3m, x=€L=8-, q=]=o+, €,=t.
t=20=;t=oO
-
-....20 L 20
Distribution load w = 2 kN/m
Requhed. Compute support reactions RA and HA, bending moments Mo and M.
sorurion. n^ =fe[r+e (l+E(,)]=]?90.+[t+oo1t+o+x06)]=13'es kN
-,r ) )x)O2
H^ =
ti" e' [r + :q ( I + 2E' )] =
rJl,zY
" s +' x[l + 3x0 6( i + 2x0'o )] = I 0's8 kN
l,t. =-*t' E,E: =-2x?0' xg.+'x0.63 =-13.82 kN.m
2"' 2
T
M" =Roi-wx8x6-HAf -MA
= 13.95x10-2x8x6-10.58x3-13'82 = -2'06 kN m
sEToN
1l
l1l
I
itl
l!
iir
ll
lrii
lir
lii
Iil
llr
il
li
+MA
Equation of parabola:
4f(L-x)x
y=
L, ' rx=lc/cos9x
. dy 4f (L-zx
'una= dx
= r
6
*Rl - L-x
-'L
LOADINGS SUPPORT
REACTIONS BENOING MOMENTS
1
M^=Mu=Mc=0
r,
-
*u Y)9j
^ 2'-
*, -
wt' rtpzrvro -
-
'
3
wt_ wi_
R^=-;, Ru=
+L
-- lt .n^ =--WI^14
u. =awf"14
M. =-
5l *f'^ 280
M- =
19
*f'" 280
M^=- 3
wft' 140
RA =qi(1+2q)P
RB =6'?(1+28,)P
H=P15Lt'e:
4f"
n. =p*eif le-rl^ " t)- l
Mu =PLB'q,
[;E
-tJ
For 03(S0.5:
rr.r-=I!e,lr-lell' t - t ,- l

LOADINGS SUPPORT
REACTIONS BENDING MOMENTS
RA
P
"2
1 sPT
H = :::-:
64f
PT,
M^ =M- =-JL
?DI
'64
w fillnnrn* w
,a
WL
R. =R^=-
., )wu
l28f
M^ =M- =- "-
192
wl- = --' 184
#,-f),B
_ 6EI.
^L"
^ oEt.
r" =* ti
-. 15 EI"
2fL
OFI
^L
]FT
"L
1EI
tvl- =--.-' 2L
-/
D _D -N
__ 45 Er,
-- 4 f)L
tvt = tvt -
ZIL
1{ FI-" "_c
' 4f L

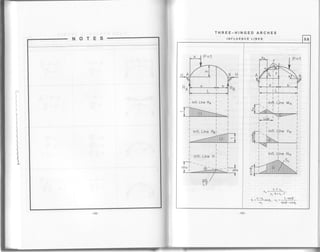
NOTES
1,"
ll
l1
llr
lli
ttit
lir
li
'[l,
ll
iil
lI
flr
fii
dl
INFLUENCE LINES
THREE-HINGED ARCHES
5.8
Infl. Line H
L.f .x,
u. =---=----*-,yk.D+xL.r
^ a- u- L.tanB
b! =JslnQk, u" =-----;-' -un lanp-cotor
I Infl. Line R4
Infl. Line Rsl I Infl. uine vk

Table 5.9
Example. Fixed Parabolic arch
civen. L=40nr" f=10m, xr=8m
Concentrated load in point k Pr = 12 kN
Required, Usinginfluencelines,compute supportreactions Ro and H^' suPPort
bending moment Mo, bending moments M" and M* axialforce No' and shear
x, 8 4xl0(40-8)8 ,,-
Sotution. a=l=0.2. yr =-----=b.+ m,
4f(L-2x) 4xl0(40-2x8)
-^ a
tanQ=-t-=--F-
Qr =30.960, sin0k =0 5i4, cosQu =9'357
Ro = S, xPo = 0'896x12 = 10 752 kN
r40
tt^ = S, x-l x R = 0.0960x-l:x l2 = 4.608 kN
' t lu
Me = Si xlxPt = -0.0640x40x12 = 30 72 kN m
M. = SixLxPu = -0.0120x40x12 = -5.76 kN m
Mr =Ra xr-He Yr-Ma =10'752x8-4'608x6'4-30'72=25 805 kN'm
Nr = Ra sin0r +He cosQr = 10 752x0 514+4 608x0'857 =9'475 kN
Vt =Rr cosQ* -Ho sinQ, = 19.752*0 857-4 608x0'514= 6'745 kN
104 -
sEToN
i1
ll
L
lL,
,,li
I
,ii
i
I
Irl
Itr
i,,
l]jl
{ii
Jill
fir
,illl
illll
INFLUENCE LINES 5.9
SrxL
Infl. Line H
Infl.1Line.M"
. 4f(L-x)x
Equation of pa€bola: y = ---- -L-
dx af(L-2x)l=lc,icosor, tanQ= . =---:,
oy L'
Rn=S,xP, H=S x!"P, M=SixLxp
oRDTNATES oF tNFLUENcE LtNEs (Sr)
x
L
RA H MA Mc
0.0 1.000 0.0 0.0 0.0
0.05 0.993 0.0085 -0.0395 -0.0016
0.1 0 0.972 0.0305 -0.0625 -0.0052
0.15 0.939 0.061 0 -0.0678 -0.0090
0.20 0.896 0.0960 -0.0M0 -0.0120
0.25 o.444 0.'1320 -0.0528 -o.o127
0.30 o.784 0.1655 -0.0368 *0.0'102
0.35 0.718 0.1 940 -0.0184 -0.0034
0.40 0.648 0.2160 0.0 0.0080
0.45 0.575 0.2295 o.o'174 o.0246
0.50 0.500 o.2344 0.031 2 0.0468
0.55 o.425 0.2295 0.0418 0.0246
0.60 0.352 0.21 60 0.0480 0.0080
0.65 o.242 0.1940 0.0498 -0.0034
0.70 0.216 0.1 655 0.0473 *0.0102
0.75 0.1 56 o.1320 0.04'10 -0.0127
0.80 0.1 04 0.0960 0.0320 -0.0120
0.85 0.061 0.0610 0.0215 -0.0090
0.90 0.o28 0.0305 0.0118 -0.0052
0.95 0.007 0.0085 0.0032 -0.001 6
1,00 0.0 0.0 0.0 0.0

STEEL ROPE
Rope deflection
w = uniformly distributed load, f = rope sag due to natural weight, (f = I / 20. L)
ltT
s = length of rope, s =./tJ +lf '
YJ
Forces and deflection:
-- Jo2nrl'n = +f
(elastic deformations are not included)
-- GI,'EAt =
i/ *
(elastic deformations are included)
E = modulus of elasticity, A =area of rope cross-section
N.* =fi'+ni R=reaction, R=wLl2
Bending moment M,* = *Ij /8 , Deflection ytu
Tsmperature:
N, =d.Ato.EA, Att =T,t-Tj, if: Ato >0 (tension), Ato <0 (compression)
d = linear coefficient of expansion
Hr_N, H, =+ Hi_N,Hi =t# , N* =uE1+n,
=M.*H
M
,o.oot-o-/+r*
ll
)
lit
il
{ii
,lr
tii
!iL
tit
,iil
,ulrr

NOTES
6. TRUSSES
Method of Joints
and
Method of Section Analysis

TRUSSES
Tables 6.1-6.4 provide examples of analysis of flat trusses.
Legend Upper chord: U
Lowerchord: L
Vertical Posts: Ui - Li
Diagonals:
' Ur-Lr*t
End Posts: Lo -U'
Load on upper chord: P'
Load on lower chord: Pb
Method of Joints and Method of Section Analysis are used to @mpute for@s in truss elements without
relying on the computer. Method of Joints is based on the equilibrium of the forces acting within the joint.
Method of section Analysis is based on the equilibrium of the forces acting from either ths left or the right
ofthesection. (I*=0, IV=0, Iu=O)
The truss joints are assumed to be hinges, and the loads acting on the truss are represented as forcos
mncent€ted within the truss joints.
METHOD OF JOINTS and METHOD OF SECTtON ANALyStS
EXAMPLEA 6.1
r-IL"; L4
Pl
.5
,b
J
6d
Mambsr Jolntg Folcoa
LoU'
LoL,
Jolnt Lo
,h*
dr,
R^ =iL(pl +p,').s+(p; +p,b).4+(n'+r,b) :+
+(r; +r"').2+(r; +p5b)], RB = n^ -!(4, *r,').
lY=R^+LoU,.sinc,o =9,
L jUt = -f,o 7.io oo (compression) .
)X = -LoU, . cosc[o +LoLr = 0,
LeLt =Logr'ooroo (tension)'
U'L,
L,L,
lV=U,I.,-nf -0, UrL, =Prb (tension).
Ix=-L0L1 +LrLr=0, L,L"=LoLr (tension)
IJrL,
Soctlon 1-1
F-
-,tp
tanp=.!::,
"=fr -0, 4 =(a+2d)sincr,.
lMo = u,Lrr,'! Roa+(P,' +rf )(a + a)= o,
u,L, = f
lRAa -(r,, +ri )(a +o)]
(comprosslon or tension)

TRUSSES
METHOD OF JOINTS and METtIOD OF SECTION ANALYSIS
Ei,A,MPLEs 6.2
Msmbor Joints Forcss
U,U,
Section 1-l (cont.)
Pt
I
l1
ryjhr
r, =(a+2d)sinB
IM", = u,urr, +RA?d -(PJ +P,b
)d = o,
u,u, = -po26 -iPI + Pi)d (compression).
U.L,
L,L,
Joint Lz
t y = u,L, - u,L, sin c, -p,b = o,
UrL, = Pro 4 Y,;-, .in 0? (tension).
lx = -LrL, +LrL, + u,L, cos c, = o,
LrL, =YrY,, -g r1-, coscl2 (tension).
(J2L3
l',L,
Sectlon 2-2 r, =(a+3d)sino,
IMo = U,L,r, - R^a + (nj +rj)1a + a)+
+(nj + el )(a +zd) = o,
u,L, =l[R^a -(pJ + pib)(a+d)-(pj +p,b)(a+2d)]
(compression).
!M,, = -L,L,h, + RA2d -(PJ +Rb)d = o,
t-,t, =i-fRoza-(rl +rf )al 6ension1.
trz'
ltrLl
r P,l =Pj, P,'=Pi, P.o =Pi, Pj =P,b,
LrLo = LrL' UoL, = UrL,
IY = UrL, - UrL, sinc, - UoL, sin cr, -Pro = 0
UrL, = Prb.r grtrr rinct, +U.L,sino, (tension).

6.3
u
--S.l-
_l
L-
'f
-L
;g
J
L
-
x
I
o
uJ
=J
ul
o
=uJ
9
J
lt
z
NOTES TRUSSES

6.4
osoc/l DSOJ/1,
J
o
=:-
117 -
TRUSSES
G
u
E
x
3
o
t!
=ITJ
o
z
ltl
J
I
=
Example. ComPutation of truss
civen. Truss3inTable6.4, L=IZm, d=2m, h=4m
h
tanoc=a=2.0, a=63.4350, costx =0.447
Load: Prb =Pob =3kN, Prt =Prt =4kN, Poo =5 kN
Required. Compute forces in truss membere using influence lines
2dZx2dtt
sorution.
^=T=t
;=;=ot, ==L"'
u
^u, =
2=9-
ei * z
-!^^ zd x P,o + 2
-Jq- x d x P,o
h ' h(0.5L) h(u.)L)
= 5 + 1.333x4+ 0.667 x3 =12'33 kN (compression)
t-,t-' = axa (Sx er" +4x Pf +3x Pob + ZxP'o + P"o
)
= 0.083x(5x3 + 4 x4 +3x5 + 2x4 + 3) = 4 73 kN (tension)
' + P"b + 2xPr" + 3x ei ++xfrb )U,Lr =:::1'd(-Pj
= 03728(-3 + 3 + 2x 4 + 3 x 5 + 4x 4) = 14'53 kN (tension)
UoLr =-gr;, =-14'57 kN (compression)

NOTES
7. PLAT rS
Bending Moments
f o r
Various Support
and
Loading Gonditions

SEToN
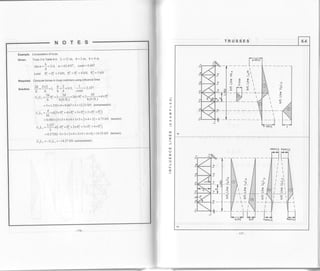
Tables 7. j-7.9 provide formulas and coefficients for computation of bending moments in elastic plates'
The calculations are performed for plates of 1 meter width
The plates are analyzed in two directions for various support conditions and acting loads'
Units of measurement: Distributed loads (u ): kN / m)
Bending moments (M): kN m/m
-120-
RECTANGULAR PLATES
BENDING MOMENTS 7.1
CASE A: CASE B:
a<b
caseA 9>2 Plateshouldbecomputedinone (short) directionasabeamof length L=a
a
CaseB !<2 ptatesnoutObecomputedintwodirectionsastwobeamsof lengths L,=a 5d lr=l
a
h
a
h
:>2
a
(h
Formulas for bending moments computation ,
: < 2 i
a )
Bending moments for any Poisson's ratio p:
v'" --fftr-ulr )M,", r1p -u, )M,,,].
'"i l-r_. tsT
Mo(a) =(ra w a b, Mo,o, =cro w a b
M.,", =p..w.a.b, M,,0, = po.w.a.b
Where: w =uniformly distributed load
G",do,0",Fo = coefficients from tables
for Poisson's ratio Pr = 0
Mi,) =+[(l-up, )M,0, +(p-pr, )M
",]'FT
Support condition
L e g e n d: :|rsssss
Plate fixed along edge.
Plate hinged along edge
t-------
Plate free along edge'
$f Plate supported on column
J
- 121

RECTANGULAR PLATES
Examplo. Computation of rectangular plate' b S 2a
Glvon. Elasticsteelplate3inTableT.2, a=1.5m, b=2,1m, t=0'04m, b/a=1'4
Uniformly distributed load w = 0'8 kN/m'z
Poisson'sEtio P=lrt=0
Requlred. computebendingmoments Mo1"i, Mo(r), M,("), M,(o)
solution. M*"i = o"wab = 0'0323x0'8x1'5x2'1 = 0'0814 kN'm/m = 81 4 N'n/m
Morb) = obwab = 0.0165x0'8xi'5x2'1= 0 0416 kN m/m = 41'6 N m/m
M",", =p"wab = -0.0709x0.8x1.5x2.1= -0.1787 kN'm/m = -178'7 N'm/m
M.n, = powab = -0.0361x0.8x1.5x2.1= -0.0910 kN'm/m = -91'0 N'm/m
BENDING MOMENTS (uniformly distributed load) 7.2
Plate supportg b/a da ([b p" Fo
1.0 0.0363 0.0365
1.1 0.0399 0.0330
1.2 0.0424 0.0298
1.3 0.0452 0.0268
1.4 0.0469 0.0240
'1.5 0.0480 0.0214
1.6 0.0485 0.0189
'1.7 0,M88 0.0169
'1.8 0.0485 0.0148
1.9 0.0480 0.0133
2.0 0.0473 0.01 18
1.0 0.0267 0.0180 -0.0694
1.1 0.0266 0.0146 -0.0667
1.2 0.0261 0.01 18 -0.0633
'L3 0.0254 0.0097 -0.0599
1.4 0.0245 0.0080
1.5 0.0235 0.0066 -0.0534
1.6 0.0226 0.0056 -0.0506
1.1 o.0217 o.oo47 -0.o476
1.8 0.0208 0.0040 -0.0454
1.9 0.0199 0.0034 4.0432
2.0 0.0193 0.0030 -0.04'12
't.0 0.0269 0.0269 -0,0625 -0.0625
1 0.0292 0.0242 -0.0675 -0.0558
1.2 0.0309 0.0214 -0.0703 -0.0488
.3 0.0319 0.0188 -0.0711 -0.0421
1.4 0.0323 0.0165 -0.0709 -0,0361
1,5 0.0324 0.01,14 -0.0695 -0.0310
1.6 0.0321 0.0125 -0.0678 -0.026s
1.7 0.0316 0.0109 -0.0657 -0.0228
1.8 0.0308 0.0096 -0.0635 -0.0196
t.9 0.0302 0.0084 -0.0612 -0.0169
2.0 0.0294 0.0074 -0.0588 -0.o147

RECTANGULAR PLATES
BEN Dl NG MOM E NTS (uniformly distributed load) 7.3
Plate support b/a c[b 9- Fo
{
1.0 0.0334 o.0273 -0.0892
1.1 0.0349 0.0231 -0.0892
1.2 0.0357 0.0196 -0.0872
0.0359 0.0165 -0.0843
1.4 0.0357 0.0'140 -0.0808
5 0.0350 0.01 19 -0.0772
1.6 0.034'1 0.101 -0.0735
1.7 0.0333 0.086 -0.0701
1.8 0.0326 0.0075 -0.0668
1,9 0.0316 0.0064 -0.0638
2.0 0.0303 0.0056 -0.0610
F#g.
1.0 0.0273 0.0334 -0.0893
1.1 0.03'13 0.0313 -0.0867
1.2 0.0348 0.0292 -0.0820
1.3 0.0378 0.0269 -0.0760
1.4 0.0401 0.0248 -0.0688
1.5 0.0420 o.0228 -o.0620
'1.6 0.0433 0.0208 -0.0553
0.0441 0.0190 -0.0489
1.8 0.0444 0.0172 -o.0432
0.0445 0.0157 -0.0332
2.0 0.0443 0.0142 -0.0338
F#4
1.0 o.0226 0.0198 -0.0556 -0.0417
1.1 0.0234 0.0169 -0.0565 -0.0350
0.0236 0.0142 -0.0560 -0.0292
3 0.0235 0.0120 -0.0545 -0.0242
1.4 0.0230 0.0'102 -0.0526 -0.0202
1.5 0.0225 0.0086 -0.0506 -0.0169'
1.6 0.0214 0.0073 -0.0484 -0.0142
1.7 0.0210 0.0062 4.0462 -0.0120
1,8 0.0203 0.0054 4.0442 -o.0102
t.9 0.0192 0.0043 -0.0413 -0.0082
2.0 0.0189 0.0040 -0.0404 -0.0076

RECTANGULAR PLATES
BEN DING MOM ENTS (uniformly distributed load) 7.4
PIate supports b/a 9." R
0o
1.0 0.0180 0.0267 -0.0694
1.1 0.0218 0.0262 -0.0708
0.o2u o.0254 -0.0707
0.0287 0.0242 0.0689
1.4 0.0316 0.0229 0.0660
1.5 0.0341 0.0214 -0.0621
0.0362 0.0200 -0.0577
1.7 0.0376 0.0186 -0.0531
1.8 0.0388 0.0172 -0.0484
1.9 0.0396 0.0158 -0.0439
2.0 0.0400 0.0146 -0.0397
@
1.0 0.0198 0.0226 -0.0417 -0.0556
1.1 0.0226 0.0212 -0.0481 -0.0530
1.2 0.0249 0.0'198 -0.0530 -0.0491
0.0266 0.0181 -0.0565 -o.0447
1.4 0.0279 0.0162 -0.0588 -0.0400
1.5 0.0285 0.0146 -0.0597 -0.0354
1.6 0.0289 0.0'130 -0.0599 -0.0312
1.7 0.0290 0.01 16 -0.0594 ^0.0274
1.8 0.0288 0.0'103 -0.0583 -0.0240
1.9 0.0284 0.0092 -0.0570 -0.0212
2.O 0.0280 0.0081 -0.0555 0.0187
wsT
1.0 0.0179 0.0179 -0.0417 -0.0417
1.1 0.0'194 0.0161 -0.0450 4.0372
1.2 0.0204 0.0't42 0.0468 -0.0325
3 0.0208 0.0123 -o.0475 -0.028'1
14 0.0210 0.0107 -0.0473 0.0242
1.5 0.0208 0.0093 -0.0464 -0.0206
1.6 0.0205 0.0080 -0.0452 -o.0177
17 0.0200 0.0069 -0.0438 -0.0152
1.8 0.0195 0.0060 -0.0423 -0.0131
1.9 0.0190 0.0052 -0.0408 -0.0113
2.0 0.0'183 0.0046 -0.0392 -0.0098

RECTANGULAR PLATES
BE N Dl NG MOM ENTS (uniformly distributed load) 7.5
Plate supports b/a cx,- (Ib F" 0o
#
1.0 0.0099 0.0457 -0.0510 -0.0853
1.1 0.0102 0.0492 -0.0574 -0.0930
0.0102 0.0519 0.0636 -0.1000
0.0100 0.0540 -0.0700 -0.r062
1.4 0.0097 0.00552 -0.0761 -0.1 t 15
1.5 0.0095 0.0556 *0.082't -0.1 155
.B
t
1.0 0.0457 0.0099 -0.0853 -0.0510
1.1 0.0421 0.0094 -0.0771 -0.0448
0.0389 0.0087 -0.0712 -0.0397
1.3 0.0362 0.0079 -0.0658 -0.0354
1.4 0.0362 0.0070 -0.0609 -0.0314
5 0.03't1 0.0059 -0.0562 -o.0279
BENDING MOMENTS (concentrated load at center)
M0,", =c".P, Mo,o, =co.P, M.,",=9".P, M,,o; =9t'P
Plate supports b/a c[^ oq p" Pr
"-t
1.0 0.146 o.146
0.179 o.14'l
1.4 0.214 0.138
0.244 0.135
1.8 0.270 0.132
2.0 0.290 0.130
TffiTtt),v.1
-l'4 + v "1
ruLL--i---l
lP '
'1.0 0.108 0.108 -0.094 -0.094
0.128 0.100 -0.126 -0.074
1.4 0.143 0,092 -0.'149 -0.055
1.6 0.156 0.086 -0.162 -0.040
1.8 0.162 0.080 -0.171 -0.030
2.O 0.168 0.076 -0.176 -o.022
-129-

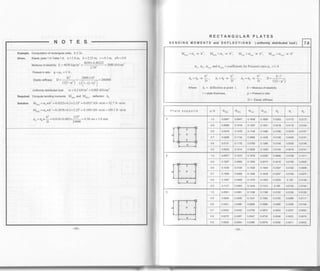
SEToN
RECTANGULAR PLATES
B E N D I N G M O M E N T S and D E F L E C T I O N S ( uniformly distributed load )
M0,", =d,.w.b'?, Mo,o, =cx'o.w.b2, M,,",=c,,", w.b', Mr,o, =cr,o, .w.b2
(,", o6, ct11"y and crr,o, = coefficients for Poisson's ratio lrr = 1/ 6
. b' b4 b4 E.tr
Ao={o w:, Ar=II w.:, Ar=Ir.*
i,
D=lr(llD
Where Ai = deflection at point i , E = Modulus of elasticity
t = plate thickness, p = Poisson's ratio
D = Elastic stiffness
Example. Computation of rectangularplate, b(2a
Given. Elasticplatel inTable7.6, a=1.8m, b=2.25m, t=0.1m, a,/b=0.8
Modutus of etasticity E = 4030 kip/in'l -
a$0: ! 18222 -2800 kN/cm2- 2.54',
Poisson's ratio P=Pt = l/6,
Erasticstiffness D= ,Et' ,, = ?800t10t,- =240000
r2(1-F') 12l 1-(l/6)' I
Required.
Solution.
Uniformly distributed load w = 0.2 kN/m'? = 0.002 kN/cm'?
Compute bending moments M0,", and Mo(u), deflection A0
M0,") =o."wb2 =0.0323x02x2.25'z=0.0327 kN m/m=32.7 N m/m
Mo,o) = cxowb2 = 0'1078x0.2x2.25' = 0.1091 kN m/m = 109. I N m/m
h4 'I' = o.:s cm = 3.g mAo =Inw
i-=0.018x0.002Y: OU
- 130
Plate supports alb 0o(") 0o(o) G,(ul 0r(o) 1lo r'I rl:
1.0 0.0947 0.0947 0.1606 0.1606 0.0263 0.o172 0.0172
0.9 0.0689 0.1016 0.1367 0.154'l o.02't8 0.0119 0.0'164
0.8 0.0479 0.'1078 0.1148 0.1486 0.0180 0.0079 0.0157
0.7 0.0289 0.1132 0.0955 0.1435 0.0158 0.0050 0.0151
0.6 0.0131 0.1174 0.0769 0.1386 0.0'148 0.0030 0.0146
0.5 0.0005 0.1214 0.0592 0.1339 0.0140 0.0016 0.0'141
1.0 0.0977 0.1 070 0.1578 0.2326 0.0606 0.0168 0.1011
0.9 0.1007 0.0889 0.1552 0.2073 0.0418 0.0165 0.0625
0.8 0.1038 0.0729 0.1526 o.1444 0.0307 0.0162 0.0406
0.7 0.1069 0.0589 0.'t498 0.1639 0.0247 0.0'159 0.o275
0.6 0.1097 0.0468 0.1470 0.1462 0.0209 0.155 0.0194
0.5 0.1121 0.0364 o.1444 0.1314 0.185 0.0152 0.0142
H
'1.0 0.0581 0.0581 0.1198 0.'1 198 o.0122 0.0126 0.0126
0.9 0.0500 0.0540 0.1031 0.'1092 0.0100 0.0089 0.0117
0.8 o.0421 0.0490 0.0866 0.0986 0.0080 0.0059 0.0106
0.7 0.0343 0.0432 0.0706 0.0870 0.0063 0.0037 0.0093
0.6 0.0270 0.0367 0.0547 0.0739 0.0048 0.0022 0.0078
0.5 0.0202 0.0294 0.0388 0.0578 0.0036 0.001 1 0.0063
-131-

NOTES RECTANGULAR PLATES
BENDING inOMENTS (uniformly varying toad) 7.7
M.,",="" * (+), r,,,,=o, * (+ M<o=e"- (+J, Mooy =0o -
a b)
2)
Plate supports b/a 0- 0b p" Fo
't.0 0.0216 0.0194 -0.0502 -0.0588
1.1 o.0229 0.0178 -0.0515 =0.0554
1.2 0.0236 0.0161 -0.0521 -0.0517
0.0239 0.0145 -0.0522 4.0477
1.4 0.024'l 0.013'1 -0.0519 4.0432
0.0241 0.0117 4.05'14 -0.0387
1.0 0.0194 0.02'16 -0.0588 -{.0502
1.1 o,0211 0.0198 -0.0614 -0.0480
0.0228 0.0178 -0.0633 -0.0435
t.3 0.0243 0.0153 -0.0644 -0.0418
1.4 0.0257 0.0132 -0.0650 -0.0396
1.5 0.0271 0.0 120 -0.0652 -o.0357
1.0 0.0246 0.0172 -0.0538 -0.0598
1.1 0.0248 0.0163 -0.0538 -0.0553
1.2 0.0250 0.0153 -0.0535 4.0510
0.0250 0.o142 -0.0529 -0.0469
1.4 0.0247 0.0128 4.0522 -0.0429
1.5 0.0245 0,01 14 -0.0514 -0.0390
'1.0 0.0172 0.0248 -0:0598 -.0.0538
1.1 0.0178 0.0244 -{.0640 -0.0535
0.0'180 o.0242 -0.0677 --0.0533
1.3 0.0182 0.0244 -0.0709 *0.0533
1.4 0.0180 0.0249 -0r0739 -0.0536
1.5 0.o't77 0.0262 -0,0765

NOTES RECTANGULAR PLATES
BENDING MOMENTS (uniformty varying toad) 7.8
t,,",="" r (+) MrF)=sr.*.[+ M.(") = p. *
[+) , r.,,, = e, .* a.b
,)
Plate supports bla cq 0b p" Fo
5 '1.0 0.0718 0.0042 -0.1412 4.0422
1 0.067? 0.0037 308 -0.0350
1.2 0.0634 0.003'1 -0.1222 -0.0290
1.3 0.0598 0.0025 -0.1 143 -o.0240
14 0.0565 0.0019 -0.1069 -o.0200
1.5 0.0530 0.0012 -0"1003 -0.0 168
6 1.0 0.0042 0.0718 -0.0422 -0.1412
1.1 o.oo47 0.0758 -0.0509 --0.1510
1.2 0.0053 0.0790 -0.0600 -0.1600
1.3 0.0057 0.0810 -{.0692 -0.1675
0.0060 0.0826 -0.0785 4.1740
0.0063 0.0628 -0.0876 -0.1790
M,(")=r, * (+), ",,,,=o,.*.(+)
M,(,)=p, *
[+), M,(,)=p, * (+), M,(,)=p, *
[+)
Plate supports bla (I^ (xb
0, F, 9,
f 1.0 0.0184 0.0206 -0.0448 -o.0562 -0.0332
0.0205 0.0190 -0.0477 -0.0538 -{.0302
,2 0.0221 0.0173 -0.0495 -0.0506 -0.0271
1.3 0.0229 0.0156 -0.0504 -{.0470 -0.0237
0.02s5 0.0137 -0.0508 -0.0431 -0.0204
1.5 0.0241 0.0120 -{.0510 -{.0387 -0.0168
E
F"
t.0 0.0206 0.0184 -0.0562 -0.0332 -0.0446
1.1 0.0218 0.0160 -{.0576 -0.0353 -0.041 1
0.0227 0,0137 -0.0580 -0.0357 4.0372
3 0.0231 0.0112 -0.0577 -0.0376 -0.0336
1.4 0.0233 0.0090 -{.0569 -{.0380 -0.0302
.5 0.0233 0,0072 -0.0556 -0.0382 4.0276
- 135 -

CIRCULAR PLATES
BENDING MOMENTq St{EAR and DEFLECTrdN 1unitomiyritstriOut"O toaat 7.9,
a = circular plate's radius
r = circular seclion's radius
t =thickness of plate
MR = radial moment
.
.,
Mr = tangential moment .
V& = radial shoar ,
R =support reaction
A = defloctiqn at conJer of ptate .
trI. = Poissonls ratio
E = modutus ofelasticity ' ]
Moment, sheaf and deflection diagrams Forrnulas
p=:, p=wnaz, R=+, v* =-3p'r2ra*2M'
,]
p
V. = ^ (l+u){t-o')
" 16n'
D-
M, = j-l 3+p-(r+
lotr.
^ Pa2,. ,,/s+u ,)a=
uo*(r-o-Jl,* -o'J,
:p)p']
D= ,qc
t2(t-1t'z)
ll1
Vi
A
p=f,, r=wna R=d; y* =-zrnlp
p-
r,r_ =ftlr+u-(3+p)p,]
rr.r, =
fi [r +u - (l +3p)p,]
Pa2 , ^' Etl
^=ab('-e')' "="G')

sorLs
NOTES
For purposes of structural design, engineering properties of soils are determined through laboratory
experimentsandfieldresearch,conductedforspecificconditionslfthesemethodsarounavailablo'
use of data provided in the norms may be accoptable'
ThemodulusofdeformationandPoisson'sfatioofsoilcanbedeterminedusingthefollowingformulas:
(l+2k^)(1+e) (l-ko)(l+e)
u'=_-_E-' .,=_-_5l
Where: ko = coefficient of lateral earth pressure (Table 1 0 1 )
e=voidEtio(Table 82)
D. = relative density ( Table 8.2 )
Soil properties found in Tables 8 2-€ 7 are provided only as guidelines'
ENGINEERING PROPERTIES OF SOILS 8.1
SOIL TYPE
SOIL PARTICLES
stzE WEIGHT IN
ORY SOIL
Cohosive soils
lgneous and sedimentary stone compact soils;
compact, sticky and plastic clay soils. Less than 0.005 mm
Coh6sionless solls
Crashed stone Coarser than 10 mm > 50 o/o
Gravel sand Coarser than 2 mm >50%
Coarse-grained sand Coarser than 0.5 mm >50%
Medium-grained sand Coarser than 0.25 mm > 50 o/o
Fine-grained sand Coarser than 0.1 mm > 75 o/o
Dustlike sand Coarsgr than 0.1 mm < 75 o/o
COMPONENTS OF SOIL
Volume Weight Moss
Nr Vo Wo.0 Mo.0
ryqFF} Vw Ww Mw
Ms
.////8i
%
Vs Ws
w M
V. V", V", V, *d V" = total volumeandvolumeof air,water,solidmatterandvoids,respectively
W, W* and W" = total weight and weight of water and solid matter, respectively.
M. M* and M, = total mass and mass ot water and solid matter, respectively

sotLs
FLOW OF WATER
WEIGHT / MASS and VOLUME RELATtONSHtpS 8.2
1. Poroaity: n =& tOO X , V=V, +V" 9. Spsclflc gravityofsollds:
c. =
q/v.
= w, o, 6_ =
M./
= M,
" Y* Y.y- p" v, p-
Whsre:
Y" and p" = unit weight and unit mass ofwater
"t.=62.41b/ft3 or 9.81 kN/m3, p* =1000kdm3
( at normal lomDeratures)
2. void ratlo:
"=t=*, V,=V"+%
3. Dogreeof saturation' 3=&-.166 o7o
4. watercontent *= &.tOO yo=M* .1ggo7o
w. M,
W+W
5. Unitweioht v=-.il
V
10. Relativedenstty: D.= e*-eo .tOOU
.100%
Where: em,e.in otld eo = 63x1rur, minimum and
in-pla€ void ratio of the soil, respectively.
T*,Tr" and To = maximum, minimum and
in-pla@ dry unit weight, respcctively.
wl6. Dry unltwelght: Td =-=:v l+w
7. Unltma$: e=+
8. Dryunltmass: er=+
Darcy's Law.
Velocity of flow: o = kr .i ,
where: ko = coefficient of permeability,
.4H..i =: = hy&aulic gradient (slope).
Actual vslocity:
-.uk".i__ko.i(l+e)tl*,*=r=l* or l)d=ry.
Where:
n and e = soil's porosity and void ratio, respectively.
Flow rate (volume p6r unit time): q = kp .i.A .
Where: A = area of the given cross-section of soil
coEFFtcrENr oF pERMEABtLrrv (ko)
SOIL TYPE ko cm / sec
Crashed stone, gravel sand 1. l0{
Coarse-grained sand 1.10{ to 1.10r
Medium-grained sand l.loj to 1.10r
Fine-grained sand l.l0* to 1 10-3
Sandy loam 1.10j to 1 10J
Sandy clay 1.10-7 to 1.10-5
Clay < 10-7

SOILS
NOTES STRESS DISTRIBUTION IN SOIL 8.3
Method based on elsstic theory
Concentrated load
Boussinesq equation:
3P
d =--
^ T rr il'
Zrcz'll+ft/zl'IL'
Where Oz = vertical stress at depth z
P = concentrated load
Uniformly distributed load
2w
O-=-
'"lt*1*t"1'l' o, =f (e, -e, *rin0, cos0, -sin0, cos0, )
Approximate method
P
,
-
--:---------:-i- ,' (B+ 22 tan O)(L +22tffi9)'
Where O, =approximate vertical stress at depth z
P =total load
B =width of footing
L=lengthoffooting, B< L
z = depth
0 = angle of intemal friction

SOILS
NOTES
Table 8.4
Examole. Settlement of soil. Method based on elastic theory'
unirs: B(m), r(m), u(m),h,(-), P,(kN), v,(tNlm';, o" (kPa), E. (kPa)
I = weight of shuctures + weight of footing and surcharge + temporary load ( live load )
zi =distance from footing base to the middle of hi layer
Lower border of active soil zone for vertical load P" has been adopted as 20% of
natural soil Pressure: 0.2d"
oiven. B=3(m), r=s.4(n), H' =5(-), ho =2(t), h' =h' =1, =1 0(m)<0'4B
H, = 4.0(m). ho = h. = fi" = h- = 1.0(m)< 0 48
yo =Tr =1.8(ton/rn')=lz r(tNlm'), E' =40000(kPa)' F' =o'10
y, = 2.0(ton/m' ), s., = 25000(kPa)' 9z = 0'72
Engineering properties of soils are determined by field and laboratory methods
Required. Compute settlement of soil under footing
P. 3000
sof ution. op =
fr =
ffi = t 85.2 (kPa), o,o = Yoho = 17'7 2'0 = 35'4(lfa)
oa" = 6p - 6'10 = 185.2 -35.4 = 149.s(kPa), 0.2o, = 0.2xY'1,1 (ho + z, ) (kPa)
oa =dixo""' (fora' seeTable8'5a) , L/B=54l30=1'8
Ht zi (m/ - /a (xi o" (kPa) 0.2o, (kPa)
H1
0.167 0.944 141.4 8.9
0.500 o.794 1 18.9 12.4
0.833 0.561 84.0 15.9
H2
1.'t67 0.391 58.4 21.6
zs = 4'5 1.500 o.282 42.2 25.5
26 - 5'5 1.833 0.207 31.0 29.6
z- =6.5 2.167 o.157 23.5 33.3
Assume: z =6.0(m), zlB --2.0' o =0.189'
o" = 0.189x149.8 = 28.3 = 0'2c..1= 0.2(5.0x17.7+3.0x19'6) = 29'5(kl'a)
Settlement:
^
1A 0.72
S=t.0(14t.4+118.8+S+.01-Y19-r t.0(s8.4+42.2+11.0)ffi=0.0065+0.0018=0.0103(m)
SETTLEMENT OF SOIL 8.4
Method based on elastic theory
Ht7
t
l= Line or, 2 =Line 0.2or, 3 =Line o"
0oo
(Ior
co,
0os
con
0ou
a
Seftlemenl: s=io r, I
i=l Ds
Where
n=numberof h-heightlayers, h<0.48
oq - additional vertical pressue at the
mid-height of h, - layer , oa = o(,i .
oao
oa, =op-or, , or. =%ho , o" =5. B,L
cri = coefficient from Table 8.5a
Yi = mit weight of soil
& = total vertical load, B < L
B = width of footing , L = length of footing
Es = modulus of defomation of soil
)t12
0=l- -" u=Poisson'sratioforsoil' l-[
Sand: p=9.76, Sandyloam: 0=0.72
Sandy clay: 0=0.57, Clay: B=9.4
Alternative ormulas
Settlement ofloads on clay due to
primary consolidarion.
Settlement of loads on clay due to
s e c o n d ary c o n s o I i d a t i o n
S='o "[H]
l+eo' '
eo = initial void ratio ofthe soil in situ
e = void ratio ofthe soil corresponding to
the total pressue acting at midheight of
the consolidating clay layer
H = thickness ofthe consolidating clay layer
s, = c,s. log(t. /t" ) , c" = o.ot - o.o:
t. = life of the structue or time for which
settlement is required
te : time to completion of primary consolidation

sotLs
SETTLEMENT OF
Coefficient di TableS.Sa
Method based on. Winklor,s hypothesis
Settlement S =
o
k..
Where
o = compressive stress applied to a unit
trea ofa soil subgade
S = settlement of unit axea of a soil subgrade
k, = Winkler's coefficient ofsubgrade reaction
(force per length cubed)
, k*,.k*"
K.. =-
k*, +k*.
EE
k... =1. k., =___:r"' hr "' h,

NOTES
For slop6 stability analysis, it is necessary to compute the factor of safety for 2 or 3 possible l
failure suffaGs with different diameters.
The smallest of the obtained values is then acceoted as the result.
sotLs 8.6
Modulus of doformation (8.) and Winkler's coeffici6nt (k*)
for some types of 6oil
Soil type Range E. (MPa) Ranse k* (Nlcm3)
Crashed stone, gravel sand cc-oc 90 - 150
Coa6e-grained sand 40-45 75 -'120
Medium-grained sand 35-40 60-90
Fine-grained sand 25-35 46-75
Sandy loam 15-25 30-60
Sandy clay 10-30 30-45
Clay 15-30 25-45
SHEAR STRENGTH OF SOIL
Coulomb squatlon: t, = c+otanQ
Where t" = shear strength
c = cohesion
o = effective intergraaular normal pressure
0 = angle of intemal friction
tanO = coefticient offriction
SLOPE STABI LITY ANALYSIS
Factorof safetyforslope F.S.21,5 to 1.8
i=n l=n
le,r, t*Q, +Rl"'.'
Wh6re 8i = weight of mass for element i
ci = cohesion of soil
Qr = angle of intomal friction
H = depth ofcut
safetv depth ofcut t" -
2c. cosQ
' y l-sin$

8.7
aeF flg i ri b
?: j" li Ff ili:,;:/+7- ! ;E ro r* E
i E-L ; E e - =- - = i
aEi€i'nF =ia :IE-; E
a3i'ai-82 Ei-g; 5€g * p
lE e1€€ E * -' E i ,€:;E ;En ; ;
5E F s gtY';L EsF 3 g
q
o@
;a F
mS
d*
NF
d6 E
;fiooOU
a
U
*E
z
oODF
iiE
Rtr
eE
?z
o$
e
o
X
3-
t*
v.
EO
q^'
oo
oo
oo
LJf'ct
o
> lrL
o
r=-J1
Lt-L_ |
l_l
qqqac!
FOOoO
aU'rolcol uo!]cnpeu
g3R33e3 R gooFooin N
.{p'6y'c11'sro}3D3 F11codo3 6u1:oeg
153 -
NOTES
2
o
<
z
=(,
o.
o
=u
r!
o
Table 8"4
Example. Bearingcapacityanalysis
civen. Rectangularfooting, B=3.6 m, L=2.8 m, BIL=1.28, smoothbase
Granularsoil, 0=300, c=0, Y=130 Lblft3 =130x0.1571=20.42 kN/m3
Loads P=2500 kN, M=500kN.m, e=500/2500=0.2m, elB=0.213.6=0.06
Bearingcapacityfactors R" =0.78, N" =20.1, N,=20
Required. Compute factor of safety for footing
Solution. q,rt=TDrNq+0.4TBNy=20.42x2x20.1+0.4x20.42>,3.6x20=1409kN/m'?
p.$.
= q,,, . B. L. R. I P = | 409 x3.6x2.8x0.7 8 I 2500 = 4.43 > 3

FOUNDATIONS
Tables 9.1-9.7 @nsider two cases of foundation analysis.
l. The footing is supported directly by the soil:
Maximum soil reacton (contact pressure) is determined and @mpared with requirements of
the norms or the results of laboratory or field soil research.
ll. The footing is supported by the piles:
Fores acting on the piles are @mputed and compared with the pile €pacity provided in the
catalogs.
lf ne@ssary, pile capacity can be computed using the formulas provided in Table 9.4.
EIRECT FOUNDATIONS 9.1
Individual column footlng Wall footing
Contact prgssurg and sqil pressurg dlagramg
rwo-wayaction: e,=fttf*ll-. wtere A=B.L, t"=*, s,=L*
One-way action
pYv"IM,
q*=++-AS,AS,
Wher6 & =P+W +2W,
Ivt., =H".t+rra^v
P = load on the footing from the column
Wr =weight of concrete, including pedostal
and base pad
W, = weight of soil
tf qd : 0; assume qd = 0
(soil cannot fumish any tensilo resistanc)
3(P...B-2tM ..- ' ! tl
2P"
2P..
q* =--=x.L

NOTES
Tables 9.1 and 9.2
Example. Direct foundation in Table 9.1
Given. Reinforced concretefooting, B=3.6m, L=2.8 m, h=3 m
A= B.L =3.6x2.8 =10.08 m" s" = L.B' /6= 6.048 m3
Loads P, = P + W, +2W, = 2250 kN, M" = 225 kN m, H = 200 kN
Allowable soil contact pressure o = 360 kPa = 360 kN/m':, f = 0.4
Requir€d. Compute contact pressure, factors of safety against sliding and overturning
P
'M.
P. IM,
sotution. q^* =
o.T
q"'=
A
-=-
2250 200x3 + 225
= 223.2+136.4 = 359.6 < 360 kPaa.*=rrg+ 6ga3
q^b =223.2-136.4 = 86'8 kPa
Factorof safetyagainstsliding I-.s
P f 2250x0 4
=IE= zoo =*
'
Factor or sarety asainst overturnins . t =
H =
#jfr =
ffiffi = + s
FOUNDATIONS 9.2
DIRECT FOUNDATION STABILITY
Factor of safety against sliding; F S. = !j" )rr
P, = total vertical loaO, !U = total horizontalforces
f = coetficient of friction between base and soil
f = 0.4-0.5
Factor of safety against overturning: F.S. = Yn*'
lvro(r
J
M,1uy = P,.B/2, M.,., =M+)H.h
M.(k) = moment to resist tuming
Mo,u, = turning moment
PILE FOUNDATIONS
Distribution of loads in pile group
Example 9.2a
Foundation olan and sections
Axial load on any particular pite:
o_P,-M,x-M_.yri--rilr-
' n.m - )(*)' -
l,:)'
& = total vertical load acting on pile group
n = number of piles in a row
m = number of rows of pile
M,,M, =moment with respact to x and y axos,
respectively
x, y = distance from pile to y and x axes,
respectively
Example 9.2a: n=4, m=3
s, 2 ^ ^f,^ - .2 ,- - ,21
Z(x) =2 3L(0.5a)- +(1.5a)-l= 6. 6.25a = t3.5a
)(y)'=2.+.1u;'=t6'
pirel: x=-1.5a, y=b, p,=+- NItl'5"*Yi-b-&
-M, *M"4.3 13.5a'2 8b') D 9a 8b
pire2: x=-0.5a, y=-b, &=J.-
M,0'5a-y+=&-M,-v.
4.3 13.5a2 8b'? n 27a 8b
pire3: x=0.5a, y=0, p, = +* Y:]1" * Yii0 = &*l!
4.3 13.5a2 8b2 12 9a

NOTES
FOUNDATIONS 9.3
Distribution of loads in pile group
X
Foundation plan and sections
Example 9.2b
vl
- 'd---*- +-l - +"-
I I | ,l I
-
--r-- 4) -
-r- - . -+.
-
Axiat toad on any particutar pite: P =
P' t lL: t lL+'' n.m - I(r)' - I(vl'
n=7, m=3, I(.f=2.3 [(")'+(2a)'+(:a1']=6'14a'z =84a2
Z$)' =2.i.(b)' =vr,
Pilel: x=-2a, y=0. R= : -:. Y':'o= I -
M'
' 1.3 84a' 14b' 21 42a
pitez: x=0, y=-b, p,= + - Yr,o - $}= & - M-
' 7.3 84a' 14b' 2l l4b
pile3: x=3a, y=b, &= + * Yi ?' - YL,o= +. p. *' 7.3 84a' 14b' 21 28a l4b
Maximum and minimum axial load on pile:
p M v n(n+l)a.m m(m+l)b n
D=u+l+ls=',s=',-ffi n.m-S"-S"' 6 -Y 6
1t1+ta.'t 1(1+lh.7
lnexampleg.2b: S = ' /" -
=28a. S =--
-'-
=l4b-' 6 6
'-
PILE GROUP CAPACITY
Ne = Ee n'm No
Converse-Labarre equation :
/ e (n-l)m+(m-l)n
E- =l-l : I'
' 90,/ n.m
For cohesionless soil Es = 1.0
Where Ne = capacity of the pile group
Ee = pile group efficiency
Np = capacity of single Pile
0 =mctand/s (degrees), d = diameterof piles,
s = min spacing of piles, center to center

9.4
G
i^
E
Eo
a-.6
s ;rooY
=oEE'68
frb*$EoEsbPo
EC'88E.€obF9
oq=oF
Egho:
f E E F $
oEEraG-dulirl
llllA
EVZ<
.r"
oo
'6
9o!E
E_o
6e
e nEoii
g-c*
F'!EE o.=
o-tb:E
O-:X.PE
< Y 5;i'o i gEE
1 gEE.d
; g;F
E'SH:&*g$u
*9,PE*h
=s-Eii ri rr^
.J ,S FJvv
i{
o
3
o
cfr<6
ie.*c
HJ.O
ll o€
&;"3
-di*F
14 i" E
o{.-:=o-9
O;rr-Ft;q-.-
E E .. e
HXO
d E! I.o'a
i !e A 5
}{ E; b = E
'l:illoZ-
6l*" fi t -F
E;;EEt--;.9;E.;',6
? EE i
'
E
q'H.e E E F
rlii-ltirl
cyq'u>H
p
o
=
tFi
=9,
c
3b' .9
--}| '<9 5.
,I
'-/ ./
-. 'ol . ./
d=4 lt*
ffit. 'g
.'Ft
' --J7;| E o
------l '€
p
r 3t'
z
o
F:
oi
{:ic=
UE
FF
zl
-;
-ooEo6
Itt
U^
;
FOUNDATIONS

FOUNDATIONS
RIGID CONTINUOUS BEAM ELASTICALLY SUPPORTED 9.5
The following method can be applied on condition that : L < 0.8. h. {/T/ q
Where E, L and h=modulusofelasticity, Iength and depth ofthebeam,respectively
E, = modulus of deformation of soil
Uniformly distributed load lw)
Soil reoction diogrom
Moment diogrom
Mo M!
Sheor diogrom
Soil reaction: qi=c[q(i).w
b/L 0q(o) 0q(r) 0q(:) dq(:) 0q(o)
0.33 0.799 0.832 0.858 0.907 1.494
o.22 0.846 0.855 0.881 o.927 1.408
0.11 0.889 0.890 0.919 0.961 1.298
0.07 0.900 0.905 0.928 0.973 1.247
Bending moment: Mi=o,t;t ,w.b.I-7
btL 0.(o) 0.(r) 0'(:) *-(r) 0.(r)
0.33 0.018 0.014 0.010 0.006 0.001
0.22 0.o12 0.01 1 0.009 0.005 0.001
0.'11 0.009 0.008 0.006 0.004 0.000
0.07 0.008 0.007 0.006 0.003 0.000
Shear: Y=a"frt .w.b.L
btL 0(u) 0"(t) o'(r) 0u(:) d(r)
0.33 0.0 -,0.019 -0.037 0.050 -0.o27
0.22 0.0 -0.016 -0.030 -0.041 -0.023
0.11 0.0 -0.014 -0.024 -0.031 -0.016
0.07 0.0 -o.012 -0.020 0.026 -0.014

FOUNDATIONS
Concentrated loads
Moment diogrom
Mo
Sheor diogrom
Bending moment: M, =c,.,,,.P.L
b/L 0'{ol 0.(r) 0.(:) d'{:) d-(r)
0.33 0.130 0.087 0.048 0.019 0.003
0.22 0.134 0.085 0.046 0.018 0.003
0.1 1 0.131 0.082 0.044 0.017 0.002
0.07 0.129 0.081 0.043 0.016 0.002
Shear: Y=4,,,, .P
b/L *v(0) d(,) 0u(:) 0'(,) 0'(t)
0.33 -0.500 0.408 -0.314 0.216 -0.083
0.22 -0.500 -0.404 -0.308 0.208 -0.078
0.11 -0.500 -o.402 ,0.302 -0.197 -o.072
0.07 -0.500 -0.400 -0.298 -0.192 ,0.069
, tl --1o.zzrf
I ttv
-wMoment diogrom
wSheor. diogrom
/41 k1'
w
Bending moment: M,=o.,,.P.L
b/L 0.(o) 0.(r) 0.(:) d.(r) 0.{+)
0.33 0.050 0.063 0.096 0.038 0.006
0.22 0.046 0.059 0.092 0.036 0.005
0.1 1 0.040 0.053 0.088 0.034 0.004
0.07 0.030 0.051 0.086 0.032 0.003
Shear: Y=oq,, .P
b/L d'(,) 0'"(:r ct--(2) G'{r) 0(ol
0.33 +0.1 84 +0.372 -0.628 -0.432 -0.1 66
0.22 +0.,|9'l +0.384 0.6't6 -0.416 -0.156
0.1 +0.1 96 +0.396 -0.604 -0.395 -o.144
0.07 +0.201 +0.404 0.596 -0.385 ,0.138

FOUNDATIONS
Table 9.7
Example. Rigid continuous footing 4 in Table 9 7
civen. Reinforcedconcretefooting, L=6m, b=2m, h=1 m, b/L=033
E = 3370 kip/in'? =3370x6.8948=23235 MPa
E, = 40 MPa, concentrated loads P = 200 kN
Required. Compute Mo, Mj, Vi, V3R
sofution. checkinsconditionr L<0.S h €/Er , 6<Ozxlxl,lTs23sl+o=6a12
Mo = c'.(0)xPxL = -0 06ix200x6 = -73 2 kN m
M3 = o(.(3)xPxL = 0'038x200x6 = 45 6 kN m
V,' = cr"(,)xP = 0 568x200 = 1i3'6 kN
vl =-0.432x200 =-86.4 kN
Concentrated loads
lP Fo..".J
P
{rrl'l I i? "lt+:rlYffi
Moment diogrom
Mo
,,-=T-r-
v--vM3
Sheor diogrom
.q,'i
L=-4 ,Y
Bending moment: M,=d,,,,.P.L
btL 0'(o) d.(,) 0-(r) 0.(r)
0.33 -0.061 0.048 0.015 +0.038 +0.006
0.22 0.065 0.052 -0.019 r0.036 +0.005
0.1'l -0.071 0.058 0.023 +0.034 40.004
0.07 -0.075 -0.060 -0.025 +0.032 +0.004
Shear: Y=o,,,, .P
b/L d"{t) su(z) o'(r) ol--(3) 0'(o)
0.33 +0.1 84 +0.372 +0.568 -0.432 0.166
0.22 10.191 +0.384 +0.584 -0.416 0.156
0.1 1 +0.1 96 +0.396 +0.605 -0.395 -0.144
0.07 +0.211 +0.404 +0.61 5 -0.385 -0.'138
5
, lP h-o.nnr*l
P
'w
Bending moment: M, =a-,,, .P.L
b/L *.(o) 0.t )
d.(:t 0.(o)
0.33 -0.172 -0.159 0.126 -0.073 +0.006
0.22 -0.176 -0.163 -0.130 -0.075 +0.005
I J -"*-J
Moment diogrom
M6
Sheor diogrom
V.'
V;
0.1 1 -0.142 0.169 o.134 -0.077 +0.004
0.07 -0.1 86 -0.17 1 0.136 -0.079 +0.004
Shear: Y=0,r,r 'P
b/L 0(r) G"(,) o'(, d.-(4)
0.33 +0.'184 +0.372 +0.568 +0.834 -0.166
0.22 +0.'191 +0.384 +0.584 +o.444 -0.156
0.11 +0.'196 +0.396 +0.605 +0.856 0.144
0.07 +0.201 +0.404 +0.615 +0.862 0.1 38

NOTES
LO)LL. FIETAINTNG
STFTUCTUFIES

For determining the lateral eadh pressure on walls of structures, the methods thal have proved most
popular in engineering practice are those based on analysis of the sliding prism's standing balance'
The magnitude of the lateral earth pressure is dependent on the direction of the wall movement. This
correlation is represented graphically in Table l O l . The three known coordinates on the graph are
,Po and Pe. As the graph demonstrates, the active pressure is the smallest' and the passive pressure
the largest, among the forces and reactions acting between the soil and the wall
construction experience shows that even a minor movement of the retaining walls away from the soil
in many cases leads to the formation of a sliding prism and produces active lateral pressure
RETAINING STRUCTURES
LATERAL EARTH PRESSURE ON RETAINING WALLS 10.1
Correlation between lateral earth pressure
and wall movement
Po = lateral earth pressure at rest
P" = active lateral earth pressure
Pr = passive lateral earth pressure
Ko, K", Ke = coefficients
Coefficients of lateral earth pressure:
K0 = coefficient of earth pressure at rest: Ko = 5 = . !
6 t-tr
md o" = lateral and vertical stresses, respectively
Poisson's ratio
Type of soil p
Sand 0.29
Sandy loam 0.31
Sandy clay 0.37
Clay 0.41
Alternative formulas: Ko = 1- sin O - for sands
Ko = 0.19 + 0.233 log (PI) - for clays
Where PI = soil's plasticity index
Where Oh
P'n
Coulomb earth pressure
^ ^ -r, ,12
r" =U.)l("Ylt, rn=U.)reyH
Where Y= unit weight of the backfill soil
t, [.1q-b),t'(o-p) 1
L'-t/*.t";st."lP:O]
K" = coefficient of active earth pressure
Kp = coefiicient of passive earth pressure
Coulomb theory
K"=
cos'(q-cr)
cos'zo.cos(c+6)
cos'(4-a)
Ko=
cos'o.cos(o-6)
Q = angle of internal friction of the backfill soil
6 = angle of friction between wall and soil (6 = 2 /30)
p = angle between backfill surface line and a horizontal line
G = angle between back side of wall and a vertical line
t, F'(o.s)'t"(a+p)l
l'-/-.(CI-D).".(P-")l
EARTHQUAKE
cos'(q-o-cl)
e = arctan
lkn / (1 - k" )]
kh = seismic coefficient, kh = AE I 2
AE = acceleration coefficient
k =vertical acceleration coetficient
-173.

ry
NOTES
Table 10.2
Example. Retaining wall 1 in Table 10.2, H = l0 m
Given. Cohesivesoil, angleoffriction Q=26''
Cohesion c=150 lb/ft'] =150x47.88=7182 Pa =7.2 kN/m'?
Unit weight of backfill soil Y = I l5 lb /ft
r
= 1 l5x 0 1571 = 18.1 kN/ml
Required. Compute active and passive earth pressure per unit length ofwall: Pn, h, Po, do
Solution. Active earth pressure;
K =ran'[+s" 9l=tun i+5' 4l=o.ro
2t l. 2l
pn = K"FI - 2cf<* = 0.39x1 8. lxl 0 - 2x7.2JdJ9 = 61.61 kN/m
PnH 61.61 l0
= 8.73 mL_
P" = 0.5prh = 0.5x61.61x8.73 = 269 kN
Passive earth pressure:
K, - ran, | 4s, + I 1-,un' I or" *
20"1-
z.so'-p " r 2) [ 2,]
pn = KoyH + 2c= 2.56x 1 8. 1 x 1 0 + 2x1.2JL56 = 486.4 kN lm
e. = u.s f :. run I or' * ! I * o, I n = 0.5 [23.04 + 486.41x10 = 2547.2 kN
' L 2/ '"j
nr++"tun[+:'+]l
d.=------,.-.-H=
:ln,+z.u"l+s +9]l
486.4+ 4x7 .2>1.6
xl0=3.48 m
3f486 .4 + 2x7 .2xl .61
LATERAL EARTH PRESSU RE ON RETAINING WALLS 10.2
Rankine earth pressure
= 0.5K.^/H' Pn = o.5KD
-1Ll-
Rankine theory ({[=0, 6=0)
The wall is assumed to be vertical and smooth
,, ^^_ocosB-r/cor'p-.os IK"=cosp+- cosp+ /cos'B cos'q
Kp=cosF?
cosp- p-cos'q
If o=0, 6=0 and 0=0:
K- =
1* sin O
= tan'[or' -9')" l+sinO 2)
K- -
I fsino-,un,l,+:o*d)= |
' l-sinO 2l K,
Exam les
't. Assumed: a=0. 6=0. B=0
2cVTE
l-f
N7 N---t'
Aq'AlI^-j+t_;_t-R/
2q V .Kp
-t-l--
AA
LH)
Cohesive soil
A/ Active earth pressure
pr =K"yH-2cd!
Where c = unit cohesive strength of soil
r,=u,"f+s"-ll. n= o'n
zt p,+z.r-l+s"-fl
2.)
Resultant force per unit length of wall P" = 0.5pnh
B/ Passive earth pressure
p', = KnyH - 2.Jrq . r, = un'[+5" 1'9
]
p- = o.sfz.tunl+s' *91*o. l. t' L 2t '')
A-
n, ++" t*[+s'+9J
:[n, * z" ,uoi+s'*9ll
2 ))

NOTES
Table 10.3
Example. Retaining wall 3 in Table 10.3, H = 6 m
Given. Backfill soil: Angle of friction Q = 300, cohesion
Unitweightof backfill soil Y- l8 kN m'
Ground water: h" = 4 m, K = 9.81 kN/m3
Required" Compute active pressure per unit length of wall: P" ,
sorution. x - rm, | +s" -9 l- ,un,1 or" -
30'l- o.:::
' | 2t | 2l
P, = 0.5K"7(H -h* )'? = 0.5x0.3::xls(6-4)'
Hh6-4
d, =l+h*-
,
tq=q.01
^
d"
= 12.0 kN
p, = K,y(H -h" )h,, = 0.333x18(6-4)x4 = 48.0 kN
d: = 0.5h* =0.5x4=2 m
r, = o.:t<" (y-"y," )hi" = 0.5 x 0.333x (18 - 9.81)x4' = 2l 8 kN
h4
d, =r= = 1.33 m
Po = 0.5Y*h'- = 0.5x9.81x4' = 78.5 kN
h4
d =_:!=,=1.33 m-33
P" = q + P, + Pr + Pi = 12.0 + 48.0 + 2 1.8 + 78.5 = 160.3 kN
. Pd,+P,d,+P,d.+Rd,
"'=---::Pj-=
12.0x4.67 +48.0x2 +21.8x1.33 + 78
160.3
= 1.78 m
a
f
;
a
o
1
Z
<
t-
tu
t(
o
U
IY
)
0
to
trt
tf.
n
L
I
IY
.{
ul
I
.t'
I(
ill
I
4.
I
RETAINING STRUCTURES 10.3
.rl o
>-l > Tl1 ^l,, Ttf a^ !l
o r <ls
"
dl _
L c +1o."
i :' r !l
; sl- a rl
L+:i
e^4o
S^=
.;sii
ot
-dF
>€iij,--O
;v"Xi< "i : o
oiFiF
il
r Tl
a-l
- !l^"
il o, l
a" *l
o-:-l
sL,
$!E
cE
o
E
F
.a
-i
:z
a:l;
r rl Y o
o El |.. _ rr
a ll ! !
=).o - - ;l-
rl
=-''^:*us=;
cr->o
;J J 3 Fi*> .H_ " :.-==ua.-. h 7 "l
oVVd-o
<nllilllll
ioiol*o;
177 -

+ >-l >-
T =l;;"?ll
Er!
!4 El
i, pil
--l
d oilori
EEo
o
llll
FFc
!2. !2" Ehh
;:x
ilil=
ai o-i E6
5
-a
E}F-F r g
XME
llll;
o'd3
o
6
o
o
o
Er6 -e-
rr F .sl
o!-;:;il
le+;-+10."
;F6RiiuloL;+o.-lo€:,i"1 =rtL.;€z--!?-
e V - +l N _l- E !
sv].-f+gr;oYo'83Lilll !?:g
d -- ,s, 3 6.
o*--;-+€
o.E-9E
'-: - s -lN g
:ia+t.-e--6d*6
<V}ZY;-
ilil"^S .o
d-F
-'179.
NOTES
o
!
I
:I
llJ
u
t
o
lu
a
3
o
tt
u,l
E
A
F
E
!J
E
u,
F
J

ll
-
oa
o!!:
: d F
"J_6-o__r_Fll
3 S- l +t N'E d=l
i x a- i i , fl..'
i + -id d*=:l
i ; A,E g E ,i_
eHrlE-'
"-i-EEE-
; q v'-." d €<VRo
llllE
&q-e
G'Ft^::
l,^ldv
l*_ lf,- rl
-l ; -Fl d E E
-lo El-l ts h
l: -l^e € 'E9l:-rJv
Esl- E.lLu g g
ERqK4A€^':o-.,:oo
r 'li ll tt ll ll
ta-tE
Eo"Eb-!!
E
o
( rl--
r ; x +1r
VqXEI'etrotr-l+-il-ll
b^rb^ELg
NOTES
o
:
3
(,
=2
<
F
u.l
E
z
o
u
tr
3
tt
o
ul
u
0-
I
F
G,
UT
J
ur
F
J

LATERAL EARTH PRESSURE ON BRACED SHEETINGS
LATERAL EARTH PRESSURE ON BASEMENT WALLS
10.6
Empirical diagrams of lateral earth pressure on braced sheetings
a/ sand: p" =0.65yHtm'l 45"-g I
2)
b / Soft to medium clay: pb = yH-2q,, q, = unconfined compressive strength, q,, = 2c
c / Stiff-fissured clay: pb = 0.2yH to 0.4yH
Active earth pressure:
^hp"
=O.sKlhj . d" _-:
t
Maximum bending momenti
M.* = 0.128P"h., d^.--0.42h
Active earth pressure:
P" =0.5K"t: , d" =+
Maximum bending moment:
r,a-.=&[r*? El" o =h E3h ['" 3 Vrh ./' "" "'V:r,
-183,

N
a
l^E-.-tl o
! E >1.>- T
" Edld >
^-: f slH
'"]r rr 3 Il:
o x t!
'- c ni E il: o'
q e o P 6lE +
r^r E : a EIE *
* .1 I :ole" hl
F. e E 3 EIE _t
,.t H ii 5tE a
I f E EIT A
F. * "P
--,1,-
Frl
o ', 9
;3
t-
lA
ol99t.o
ul I
',=t F
3tP
IE
--tF-
+t+
r ElE
:srl-Poil-ilE
;.od ;" 1>to-o
:Fo-:=r-.F6;lqs-'l
-cbxlE
c:_-6r!>
ilAE
> ij g -:_ -.. t.: B > el N..el^,3
oE.bE'n="^
o Q E;.w li o €
-Egii-:--E---,8U, g gE- E =* F e
:6E+h:F
-o*kFdF
g;3 3 e 3
ttii.=t3tl
3t€ a" I e.'
o
o
.9
b
'il
Hlr
'^lL
€l
+
Ft4
Nl.r
E
;
o
o
o
o
E
.E
o
F
N
'l la
VI
>lx
htlN
I
.rlN
E.
o
c
E
o
I
E
U
ao
o
(
q
o
o
o
o
o
o
9)
I
o
E
e
a
ll
q
-185-
NOTES
at,
J
J
B
o
=2
:F
U
t
g.
IJJ
lu
J
;z
(J

NOTE
Table 11.2
Example. Cantilever sheet piling 2 in Table 11.2, H = l0 m
Given. Soil properties: Q, =32", c, =0, Tr =18 kN/ml
Q, =340, c, =0, % =16 kN/m3
K,.Y,H 0.283lgyl0
-r--
(K" - K. )Yr 3.254x t6
P, = 0.5K"^1,H2, = 0.5x0.283x1 8x 10x0.98 = 24.96 kN,
P -0.5(Ke K,.)y,(Do-2. )': =0.5x3.254yt6(Do-2,)
IVto = O (condition of equitibrium)
',
(f .o,).', (o, -]) -* Jro, -,,) = o
zzo.:[f +r.]+z4.e6Do *26.031(Do -2, )' = 0
8.68(Dn - z, )' = 921.0 + 301.26D o
Using method of trial and error:
assume Do =8.3 m, (8.3-0.98)' =t96.16*rO..'tx8.3, 394.19 =393.18
D = l.2Do =1.2x8.3 =9.96 m
r.- = t [+., *,,)* v,(?
",
*,,
)
- o.s
1r,, -
"^.l
r*Z(?)
= zre.: ($ + o.rs * t.+)* z+.0 e(l"o.n, * r.o) - o. r', zs+ xr e xs +, (!l =' rn r.o u*
B=0, o(=0, 6=o
per unit length of sheet pilingRequired. Compute depth D and maximum bending moment M,."*
sorution. K' ="''(or'-!)=
'*'(*" -!)=,ro,
r", = tm'[+s' -9.) =
""'[or' -1L] = o,"
r", = tm' (+5' n Q,
)
="',(or, *fj =r.rrt,
P, = 0.5K,,T,H' = 0.5x0.307x18x10'? = 276.3 kN,
CANTILEVER SHEET PILINGS 11.2
Equation to determine the embedment (D0 ) :
- (r,-r,)vrir
6(4H+lD[
Maximum bending moment :
/
-
| 1t p I
M."=P[H+;iG;fi]
^ 4H+3D
-' -'oH +4o,
For single Pile
o-(K,-K-)YdDi r- =.f"n?' 3{4H +3D") [ 3
where d=pilediameter
D = (1.2 to I.4) Do for factor of safety at 1 5 to 2 0
'(Kp;Ko)T2Qo-74
Earth pressure:
R = 0.5K"^YH'
P: =o.5K,,YrH z' zt=
P, = 0.5(Ko. -r", )T, (Dn -,,)'
Equation to determine Do: lMo = 0
ef {*o,l*e,f o.-11-e jro,-, t=o
3 ") - 3l
D =(1.2 to 1.4)Do for factor of safetyat 1.5 to 2 0
m = point of zero shear and maximum bending moment
Maximum bending moment
(H ,(2
*.- = R
[;.
z,+ zz
)+P,l:z'
+ zz
)
(,
-os(r,-r")rzi [5J
186 -

w-
NOTES
Tablo 11.3
Example, Anchored sheetpilewall in Table 11.3, H=15 m
Given, Soil propedies: 0, =30', cr =0, ^L=20 kN/m3, 02 =320, cz =0, T, =18 kN/ml
Requrred. compute deprh D ano
'*,'r.lJ"oo,"n"rl"l""i;t:* ,:,;fi"Tn-
",",Solution.
r", = m' f +s' -9 l-,un' f +s' -4)=o.rrr, K. = tan' | +s' -9 1 =,-, i +r" -14 I = o.ro,"' 2) 2 ) ( 2l '-
[- z)--"
K,. =r*'f +so+91=,un'[+:"*14 ]=r.rro, K", -K,. =2.s48
"' 2) l. 2 )
Forces per unit length of wall
P, = 0.5K",T,dt = 0.5x0.333x20x1.2': = 4.8 kN
P, = 0.5K", y, (H + d) (H - d) = 0.5 x 0.333 x20x (rs + r.2) (r s - 1.2) = 744.4 kN
. (H -d)(2H +d) {r5 - t.2 )(2x t5 + 1.2 )
' 3(H+d) 3(ts+t.2)
p:
=0.5K",rrHz, =0.5x0.307x20x15x1.74=80.13 kN, , =#HE =o'r!#frirt =r.r,
Fot Q2 =32' : x = 0.059H = 0.059x15 = 0.885
Ivr, = o, R(H-d+x )+r, 4-p,a, -p, (H-a-1) = o
R(r5 -1.2+0.885 )+ +sx! -t ++.+x8.86-80.13fl5-r.r* t tol
= o, R = 527.46 kN
3 z ) -'
T = (Pr + P, + & ) - R = 4.8 + 744.4 +80. l3 - 527.46 = 301.87 kN
o"=r, * i|,,E =, ro*.@=7.58m. {assumed
V(K' -K..)Y,, Y2c48xl8
D= l.2Do =1.2x7.58=9.1 m
i e,+e,+e.-r /4J+i44l+sot3-jot-87
, _-
! 0.5(Ke - K" )y, Y 0.5v 2.948x 18
r.* = (q *r,)(4*,, *,,) *r,(2,,*".)*r(+r-d+2,+2.)-0s1r," -r", )i,* (f)
= {
+. s + za.+; (ll + t.t a + +.+6)+ Bo x(}t.t + * +.+al - ro,.r, 1
r, -,., + 1.7 4 + 4. 46)
-0.5x2.g48xt8x4
46'
= 2019.4 kN .m/m
o
=ul
J
;
F
u
lll
a
U
o
z
s' slo
+
-
i î+.1
*-l:'
î bT.
B E --l- )z
qP"i;
:!+aGl, l
> X I 19 Nl-
; : tFt-j-- Nl
E E tit .,
J E l'"ll oi
9 : l+lr +
6El^^li^
E -lTlv.. N
t E l'-|tr; I* F +F +
-oNl'":.
F+
,9b;o,-
ÎEE-
xc
.!6
"nxEn-o<Htr>d
o
E
g
ll.,
I l>tl^
lo< | Fa
lel I
lli
I lv-
+
N
I
a
^lil':
N.'",
il Nilo a
x+
o il
-
ll
- E ----
er^.| r -
!.. E V
(d,b
or{c 'Ft,. 9
E^-O
h':o
o:
!xE
9+c
*+o:F
ffsL
I
o
I
o
T
ts
ci
N
-
d
N
I
N
o
Nl^
',''
=lJv ;l I
v't vl .
rr ll4
oiil
_Nl
F,z
> -l O
.- it o
V Jl- e
d Nl+ X
^^ Yl; g
it o
EII F
*d B
VEv] .- -a
,,,'rl
or-dx
o
E
u
N
o
o
.N
I
:a
if,Y

NOTES
Lzr L3. P
and
TUNN
IP rS
ELS
Bending Moments
for
Various Static
Loading Conditions

This chapter provides formulas for computation of bending moments in various structures with
rectangular or circular cross-sections, including underground pipes and tunnels. The formulas
for structures with circular cross-sections can also be used to compute axial forces and shea6.
The formulas provided are applicable to analysis of elastic systems only.
The tables contain the most common €ses of loading conditions.
TUNNELS
RECTANGULAR CROSS-SECTION 12.1
, I,h
I,L
+M =tension on inside of section
ffio
q*w
ri w(2k+3)-ak
M- =M. =-- ': '
12 k'+4k+3
t? c{2k+3)-wk
M =M.=--.",12 k'+4k+3
For q=Y
.- r2 k+3
M =M.=M^=M,=-ia. ,
12 K'+4k+3
PT 4k +g
M =M. =-:-1. : - -
24 k'+4k+3
PL 4k+6
lYl =lvlj =--. :
24 k'+4k+3
FOr K=l
1?
M =M. =-
-- PL
192
v-=v,=- 7 Pt
t92

TUNNELS
I-
NOTEST R E C TA N G U LA R C R O S S- S E C T IO N 12.2
rtFI
FI
F
F
H
f
llh-i(
l2(k+l)
Mo =M" =lfo ={"
For k=l and h=L
M" =M. =M^ =M, =_I::
24
Mo = o.l25ph' - 0.5 (M" + Md )
M., -M" -- Ph't(2k+7)
'"b o0(k, +ak+l)
M -M, -- P!'!(lk+S)
60(k':'4k+3)
For k=l and h=L
M'=M,=-lPh'. M-=M --llph/160 480
uo = o.o64ph'? -[M" +0.s77(Md -M" )]
-L2t.
a =
P" I ltotr' -:u'I60h'
^ pbak (. 45a -2b D=:-n-_a-_b-_l
2h' 270a )

PIPES AND TUNNELS
Table 12.3
Example. Rectangular pipe 7 in Table 12.3
Given. concreteframe, L=4m, H=25 m, hr =10 cm, h, =lQ s6
b =1 m (unit length ofpipe)
- bhi looxlor bhi loox2or
l.= J=--EJJJCm lt=-=- =OOOO/Cm
'1212"1212
Uniformly distributed load w = 120 kN/m
Required. Compule bending moments
- I.H 66667x2.5
Sotution. k=I='--'" - -
=5.0, r=2k+1=2x5+1=11
I,L 8333x4
m = 20(k+2) m = zo(k+2)(6k' +6k+l) = 20(5+2)(oxs' +oxs +t) = zs:+O
or = 138k2 +265k+43 = 138x5'] +265x5+43 = 4818
o, = 78k'? + 205k + 33 =78x52 +205x5 + 33 = 3008
oc: = 81k2 + l48k + 37 = 81x5'? + I 48x 5+37 =2802
r. = - 9l l* o'
l= ''o-10' I
t.
*-1!lL]= -22.56 kN.m , M.
' 24[r m) 24 ll 25340]
M.=_:fr1*s.l=rro_10'r+._rgol)=*,u.rr^ -, Ml
' 24r m) 24 !ll 251401
y", =_wL'f
:t<+t
*a,_t20ta'z(l"s+ 2802
)__125.2 kN.m
"' 24 r m) 24 ll 25340)
= -
*f f 1- ", ) = +7.e2 kN.m
24 r m)
=-*f 1,1- "'J=+2.24 kN.m
24 r m)
*",=-9[U-b)=-roz.++r<n m. Mno
"' 24[ r m)
M . =-r{ g.
--l2ox4:.
ee2
=-6.24 kN.m
"' 12 m 12 25340
M . =_
*L' f
3k*t _gr) _ _r20x4' [:xs+t r
qqz']
=_l19.44 kN.m
"" 24 r m) 24 ll 25340)
=-*f .
*,
=-17.76 kN.m
12m
R E C TA N G U L AR C R O S S_S E C TI O N 12.3
Th
I'L
r =2k+1
m=zo(k+z)(6k'+6k+1)
+M =tension on inside of section
r2
Ir Ir
l.
r2
l2
4 I1
tv
ffi wti t
,^=-i ;, M. = M. = M, = ,{.
..,t2 tl+l
r, =-li -'';'. Mo,=Moo=Mu.=Vo,
lt -^t -n
M"
wf-'f t o, ) .. sL rt cr, l
r. tvl =-- _-
-
i
24r m) ' 24r ml
=-'"l,]*c'1. 1r4.=-"1'i1-o, 1
24r m) 24lr n)
wL'z/3k+1.a, .. wL'c,+jNl,
24 r m) "' l2 m
_ wt-'(:l*t cr,) n, wL' cro
r. i,_ =--
-24t r m) "' 12 m
wt-'l.lt<+t . o, 1
lvri< = --l" 24[ r m)
," wL'l:t<+t o,)lvi,, = --l' 24 r m)
M.
Mn,
Mo,
dr =138k' +265k+43, tlc3 =81k' +148k+37
c: = 78k'?+205k+33, cx4=27k2 +88k+21

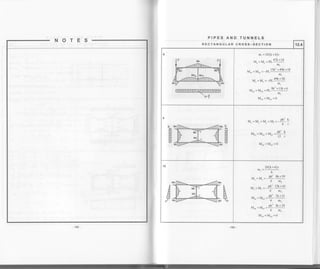
AND TUNNELS
RECTANGULAR CROSS-SECTION 12.1
ry
m' - 24(k+6)r
Ira" =Na. =Pl,l4llsml
Mur = Mrz = -rr
l5k'+49k+18
ml
M" = M, = -PL
49k+ 3o
ml
Mae = Maz = r"
9k'+ 11k+6
ml
Mon =Mon =0
R
H
FI
tt|
t-t
.h2 L
M, =M" =M. ="r=-?.;
M,, =M.. =fr,f,, =d.!"' 12 r
Mr.=Mon=0
A
H
F
h
H(p
20(k+6)r
In, =__T-
N,t" = 1,,t" = -Pht .
st*sg
of,r
M- =M" =-Ph'z,12k+61
6m,
Mo, = Mor - P!' 7k+31
'om2
Mao=Mo, -Ph:
jk+29
oh:
Mo, =Mun =0

Structural engineering formulas

Structural engineering formulas

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (16)

Similar to Structural engineering formulas

Similar to Structural engineering formulas (20)

Recently uploaded

Recently uploaded (20)

Structural engineering formulas