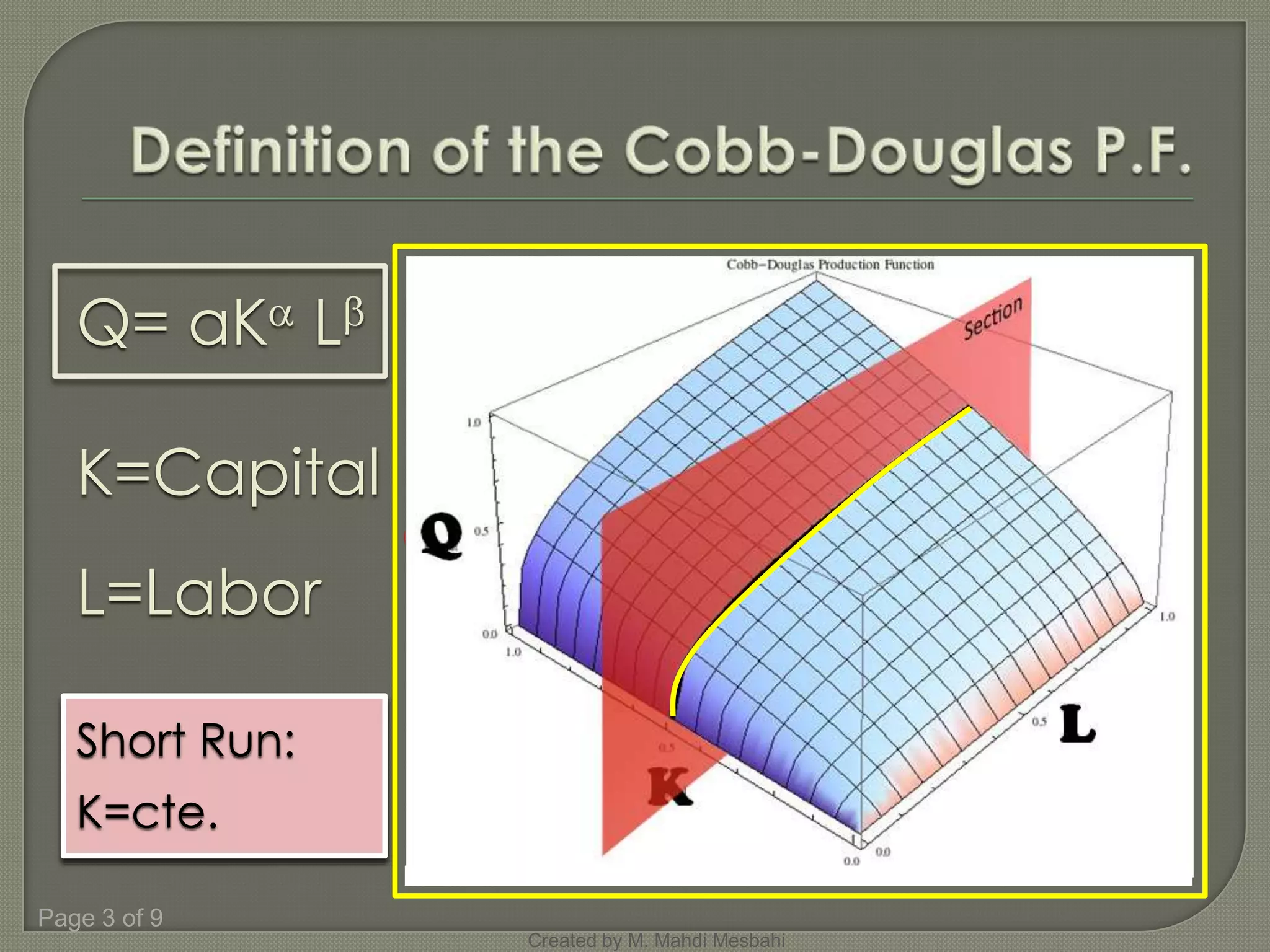
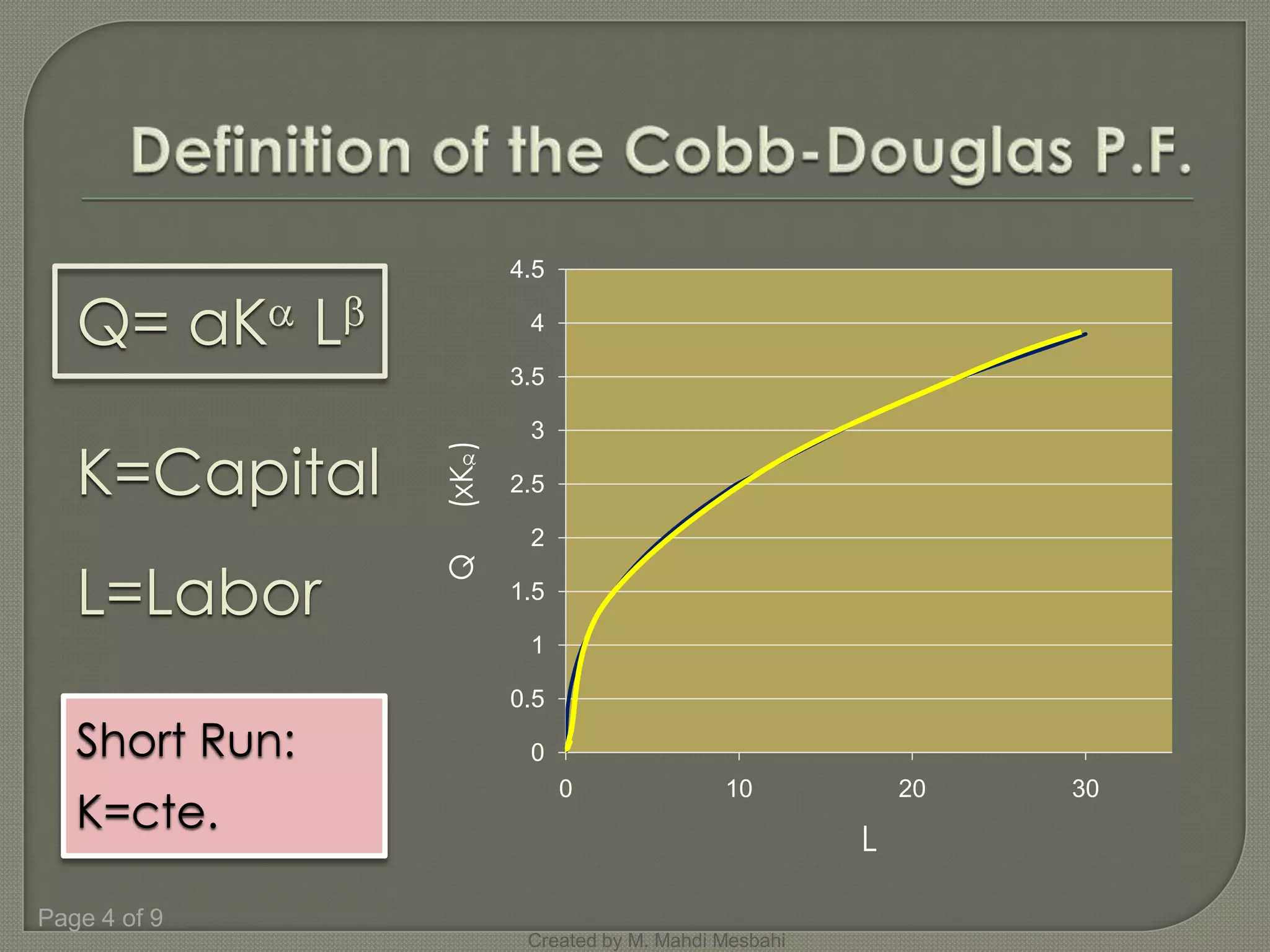
The document discusses production functions and their relationships. It shows that a production function relates the maximum quantity of output (Q) that can be produced from given amounts of inputs (capital K and labor L). The production function is represented as Q=f(K,L). It then derives and graphs the equations for total product (Q), average product (APL), and marginal product (MPL) based on the Cobb-Douglas production function of Q=K^0.3 L^0.8. It finds that average product is maximized when average product equals marginal product.