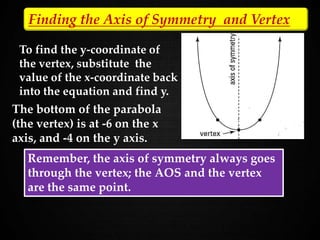
Today's math lesson will cover graphing quadratic functions by finding the vertex and axis of symmetry. Students will graph 6 quadratic functions as class work. It is recommended to take good notes and bring a calculator every day. Notebooks will be submitted next week. The document then reviews key aspects of quadratic equations and functions, including their standard forms and how to find the x-intercepts, axis of symmetry, and vertex of a parabola. Students' assignment is to graph equations and pay attention to how changing a, b, and c values affects the parabola shape.

1. Today:
STAR Math Update
Vertex and Axis of Symmetry:
(What they are & how to find them)
Graphing Various Quadratic Functions
Class Work: 6 Graphs
2April

2. But first, a sample of
Additional Resources Available for download at the
v6
math site:
Class Notes Section of Notebook, pls.
It is strongly recommended that you take good notes
today. Also recommended: Bring a calculator everyday
BTW, Notebooks will be submitted next week. Get them
organized (they should be already)

3. Textbook & Practice
Problems/Quizzes with Answers

6. Class Zone
Class
Notes
Section

7. Quadratic Equations vs. Functions
Remember, the standard form of a quadratic equation is:
ax2
+ bx + c = 0
Since the solutions/roots to a standard equation are where the
line crosses the x-axis, the y value is always zero at this point.
As such, we can substitute y for zero: y = ax2
+ bx + c
Since the y variable is dependent on the x, or is a function of
x, we can substitute the y for the function of x, or (f)x:
(f)x = ax2
+ bx + c
Regardless of which form is presented, the problem is solved
in the same way.
***Quadratic Equations are solved algebraically. Quadratic
Functions are solved graphically.

8. 1. To solve and graph a quadratic equation, we need to know
where the graph either touches or crosses the x and y axis:
These, of course, are the intercepts.
In order to graph a quadratic function, we must know to use
the equation to plot the key parts of the parabola. Then, we
basically connect the dots to complete the graph. Here are
those key pieces and how to find them.
1. We will learn a number of ways to
find the x-intercepts, but for now we
find them by factoring the quadratic
equation in standard form.
Graphing Parabolas & Parabola Terminology
The solutions are the x-intercept(s)

9. 2.Axis of Symmetry:The axis of symmetry is the verticle
or horizontal line which runs through the exact center
of the parabola.
Graphing Parabolas & Parabola Terminology
Other Important points on a Parabola:
Another helpful point
to remember about the
axis of symmetry is
that is is always
halfway between two
x-intercepts

10. 3. Vertex: The vertex is the highest point (the maximum),
or the lowest point (the minimum) on a parabola.
Notice that the axis of
symmetry always
runs through the
vertex.
Graphing Parabolas & Parabola Terminology
If the value of a is negative, the parabola will open
downward, and the vertex will be a vertex maximum

11. Vertex Minimums and Maximums
What do the vertex
minimum or
maximum tell us in
terms of the function's
domain and range.
The information regards the range of the function:
No y value can be greater than the vertex
maximum, nor less than the vertex minimum.

12. Finding the Axis of Symmetry & Vertex
The center of the parabola crosses the x axis at -6. Since the
axis of symmetry always runs through the vertex, the x
coordinate for the vertex is -6 also.
The formula for finding the axis of symmetry
x = - b/2a
Our quadratic function is: y = x2 + 12x + 32
But, we still don't know
where the vertex lies on the
vertical (y) axis.

13. To find the y-coordinate of
the vertex, substitute the
value of the x-coordinate back
into the equation and find y.
Finding the Axis of Symmetry and Vertex
y = -62 + 12(-6) + 32.
y = 36 - 72 + 32. y = -4
The bottom of the parabola
(the vertex) is at -6 on the x
axis, and -4 on the y axis.
Remember, the axis of symmetry always goes
through the vertex; the AOS and the vertex
are the same point.

14. Finding the Axis of Symmetry and Vertex
Find the x-intercepts, axis of symmetry & vertex for the
following:
x2 + 2x – 3 = 0 –2x2 + 6x + 56 = 0 2x2 + 2x = 3
Lastly,
Solve a quadratic equation to
find the value of x
f(x) = -x2 -4x - 12
Today's Assignment: Graph
equations, paying special attention
to how the a, b, and c values change
the shape of the parabola

16. 2. The Microhard Corporation has found that the equation
P = x2
- 7x - 94
describes the profit P, in thousands of dollars, for every x
hundred computers sold. How many computers were sold if
the profit was $50,000?
f(x) = x2 + 2x + 8
f(x) = 2x2 + 4x + 2