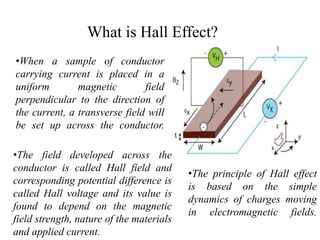
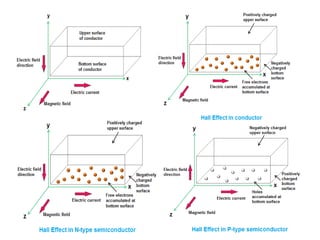
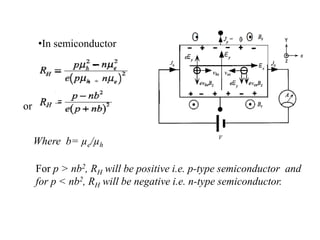
The document discusses the Hall effect, which is when a conductor carrying an electric current is placed perpendicular to a magnetic field. This causes the charges in the conductor to experience a force perpendicular to both the current and the magnetic field. This displacement of charges establishes a voltage difference known as the Hall voltage across the conductor. The Hall effect can be used to determine various properties of materials like charge carrier types and densities. Precise measurement techniques like Van der Pauw and Hall coefficient calculations are used to characterize semiconductor samples.

1. Hall effect
Keshav Kumar Sharma
M.Tech (SSM)
2017PHM2215

2. Discovery
• Observed in 1879
• Edwin Herbert Hall
• Discovered 18 years before the electron
2

3. What is Hall Effect?
•When a sample of conductor
carrying current is placed in a
uniform magnetic field
perpendicular to the direction of
the current, a transverse field will
be set up across the conductor.
•The field developed across the
conductor is called Hall field and
corresponding potential difference is
called Hall voltage and its value is
found to depend on the magnetic
field strength, nature of the materials
and applied current.
•The principle of Hall effect
is based on the simple
dynamics of charges moving
in electromagnetic fields.

5. Hall voltage (VH)
For a simple metal, the Hall voltage VH can be computed by
setting net Lorentz force to zero.
Using,

6. Hall coefficient
•The unit of RH is expressed as m3/C. This concludes that
the type of charge carrier and its density can be
estimated from the sign and the value of Hall co-
efficient RH. It can be obtained by studying the variation
of VH as a function of I for a given B.
•The above equation also concludes that Hall effect
differentiates between positive charges moving in one
direction and negative charges moving in the opposite.

7. •In semiconductor
or
Where b= µe/µh
For p > nb2, RH will be positive i.e. p-type semiconductor and
for p < nb2, RH will be negative i.e. n-type semiconductor.

8. Van der Pauw Measurements
•The resistivity of the material
•The doping type (i.e. whether it is a P-type or N-type material)
•The sheet carrier density of the majority carrier (the number of majority
carriers per unit area).
•The mobility of the majority carrier
The following properties of the material can be calculated:
•Sample geometry

9. •Requirements
1. Permanent magnet, or an electromagnet (500 to 5000 gauss)
2. Constant-current source with currents ranging from 10 μA
to 100 mA (for semi-insulating GaAs, ρ ≈ 107 Ω·cm, a range
as low as 1 nA is needed).
3. High input impedance voltmeter covering 1 μV to 1 V.
4. Sample temperature-measuring probe (resolution of 0.1 °C
for high accuracy work).
ρ = sample resistivity (in Ω·cm)
d = conducting layer thickness (in cm)
I12 = positive dc current I injected into contact 1 and taken
out of contact 2. Likewise for I23, I34, I41, I21, I14, I43, I32 (in
amperes, A)
•Parameters

10. V12 = dc voltage measured between contacts 1 and 2 (V1 -
V2) without applied magnetic field (B = 0). Likewise for V23,
V34, V41, V21, V14, V43, V32 (in volts, V)
•Resistivity measurements
•Apply the current I21 and measure voltage V34
•Reverse the polarity of the current (I12) and measure V43
•Repeat for the remaining six values (V41, V14, V12, V21, V23,
V32)
Eight measurements of voltage yield the following eight
values of resistance, all of which must be positive:
R21,34 = V34/I21,
R12,43=V43/I12,
R32,41 = V41/I32,
R23,14 = V14/I23,
R43,12 = V12/I43,
R34,21 = V21/I34,
R14,23 = V23/I14,
R41,32 =V32/I41.

11. The sheet resistance RS can be determined from the two
characteristic resistances
RA = (R21,34 + R12,43 + R43,12 + R34,21)/4 (vertical)
and
RB = (R32,41 + R23,14 + R14,23 + R41,32)/4 (horizontal)
RS = (RA+RB)/2
Resistivity
ρ = πd*RS/ln2

12. Hall measurements
•Apply a positive magnetic field B.
•Apply a current I13 to leads 1 and 3 and measure V24P
•Apply a current I31 to leads 3 and 1 and measure V42P
Likewise, measure V13P and V31P with I42 and I24,
respectively.
•Reverse the magnetic field (negative B)
Likewise, measure V24N, V42N, V13N, and V31N with I13, I31,
I42, and I24, respectively.
Steps for the calculation of carrier density and Hall
mobility are:
1.Calculate the following:
VC = V24P - V24N, VD = V42P - V42N,
VE = V13P - V13N, and VF = V31P - V31N.

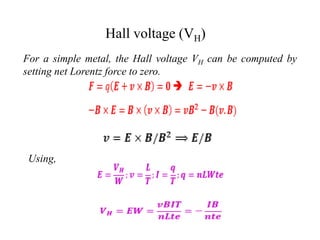
13. 2.The sample type is determined from the polarity of the
voltage sum VC + VD + VE + VF. If this sum is positive
(negative), the sample is p-type (n-type).
3.The sheet carrier density (in units of cm-2) is calculated
from
ps = 8*10-8IB/[q(VC + VD + VE + VF)]
if the voltage sum is positive, or
ns = |8*10-8 IB/[q(VC + VD + VE + VF)]|
if the voltage sum is negative,
where B is the magnetic field in gauss (G) and I is the dc
current in amperes (A).
4.The bulk carrier density (in units of cm-3) can be
determined as follows if the conducting layer thickness d
of the sample is known:
n = ns/d p = ps/d

14. 5.The Hall mobility μ = 1/qnsRS (in units of cm2V-1s-1) is
calculated from the sheet carrier density ns (or ps) and the
sheet resistance RS.
Hall coefficient
Eight resistances on the application of magnetic field are
R24,13 = V24P/I13, R42,31 = V42P/I31, for (+)B
R13,42 = V13P/I42, R31,42 =V31P/I42.
R24,13 = V24N/I13, R42,31 = V42N/I31, for (-)B
R13,42 = V13N/I42, R31,42 =V31N/I42.
RH = d/8B*[R24,13(+B)-R24,13(-B)+R42,31(+B)-
R42,31(-B)+R13,42-(+B)- R13,42(-B)+R31,42(+B)-R31,42(-B)]

15. Hall measurements setup