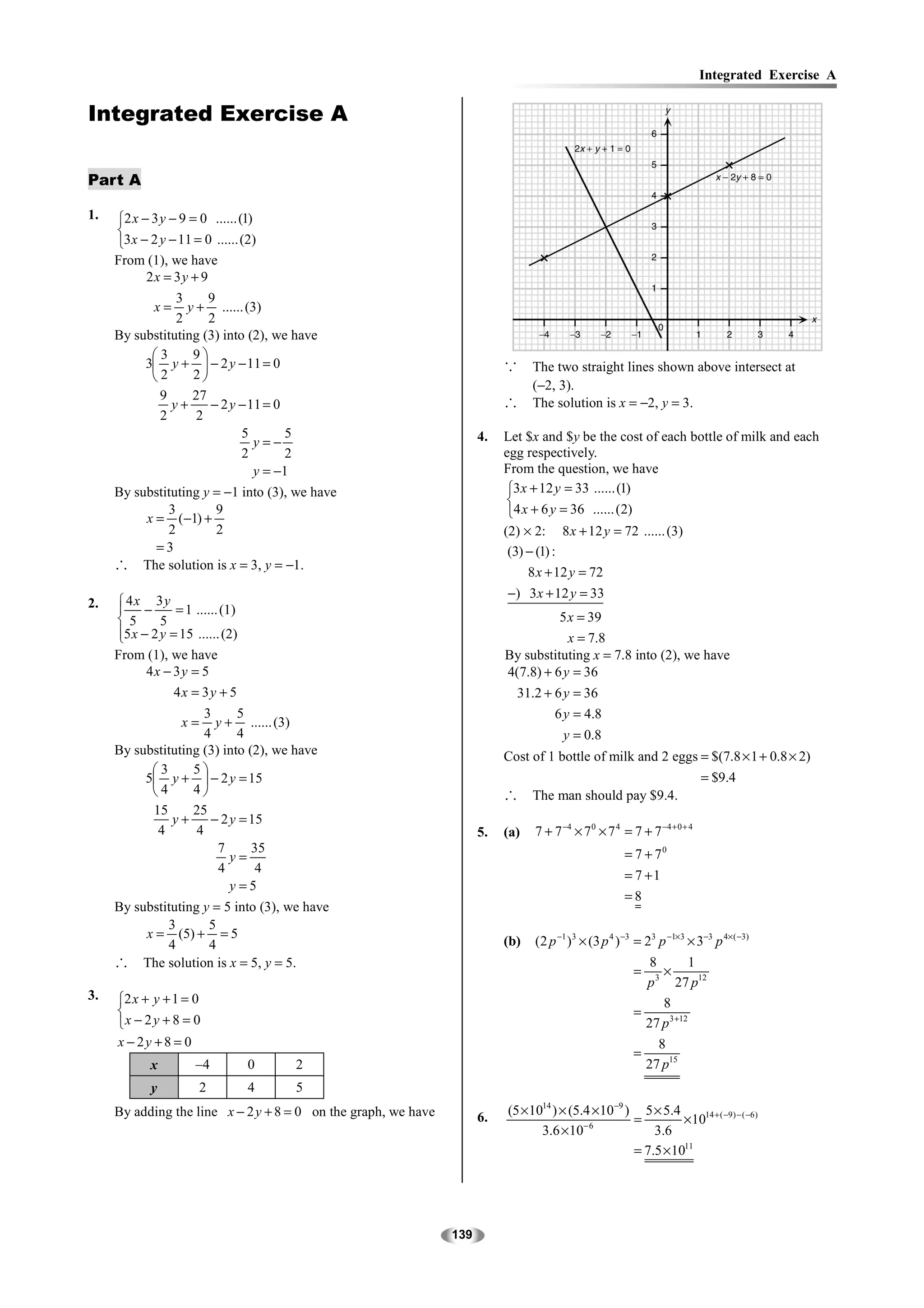
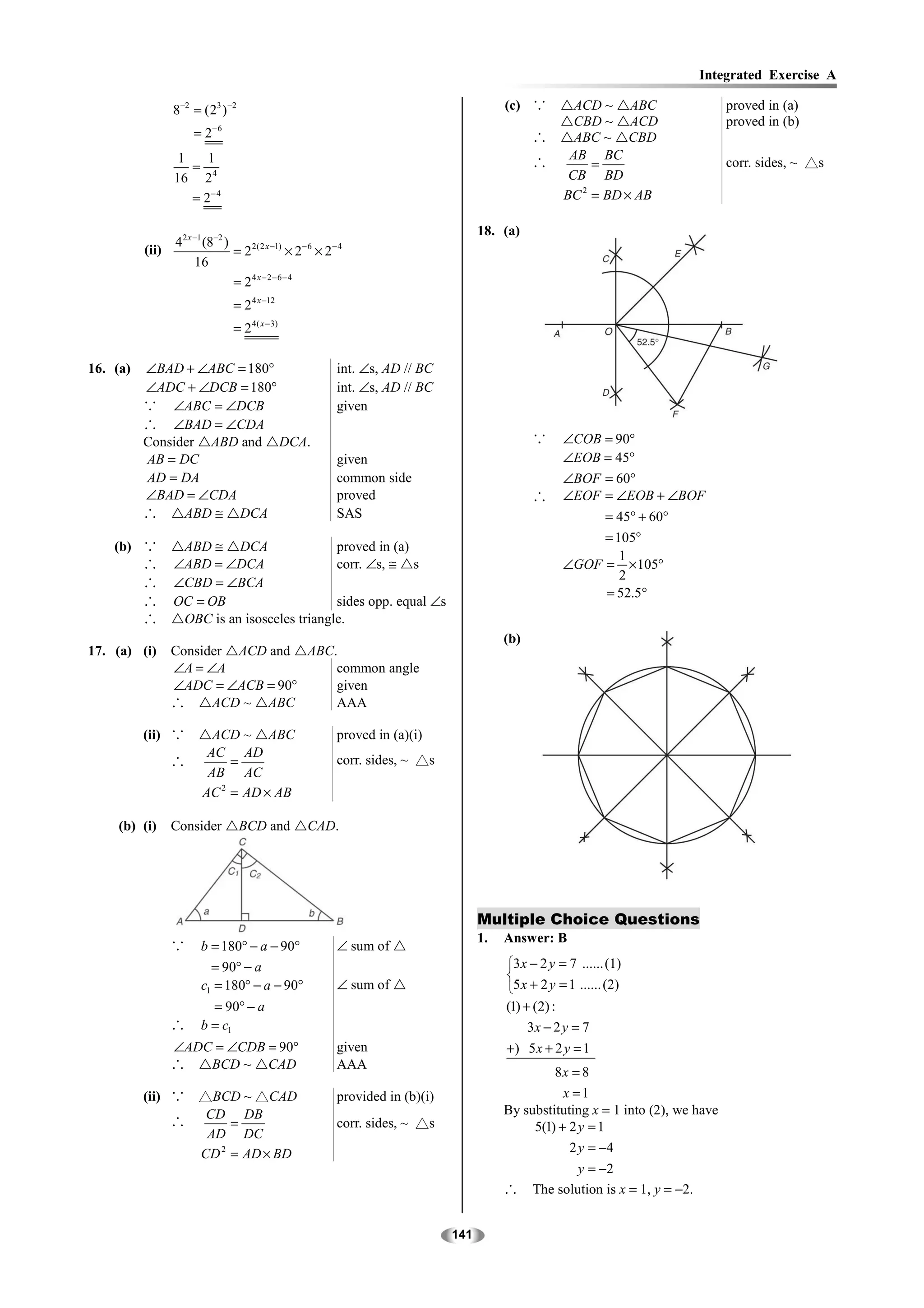
1. The document contains examples solving systems of linear equations and linear inequalities arising from word problems about mixtures, costs, graphs of lines, and similar contexts. 2. Similar figures and corresponding parts of congruent triangles are used to solve for missing lengths and angle measures. 3. Place value and binary and hexadecimal number systems are explained.

1. Integrated Exercise A
Integrated Exercise A
Part A
1. 2 x − 3 y − 9 = 0 ...... (1)

3 x − 2 y − 11 = 0 ...... (2)
From (1), we have
2x = 3y + 9
3 9
x= y + ...... (3)
2 2
By substituting (3) into (2), we have
3 9
3 y +  − 2 y − 11 = 0 ∵ The two straight lines shown above intersect at
 2 2
(−2, 3).
9 27
y+ − 2 y − 11 = 0 ∴ The solution is x = −2, y = 3.
2 2
5 5 4. Let $x and $y be the cost of each bottle of milk and each
y=−
2 2 egg respectively.
y = −1 From the question, we have
By substituting y = −1 into (3), we have 3 x + 12 y = 33 ...... (1)

3
x = (−1) +
9 4 x + 6 y = 36 ...... (2)
2 2 (2) × 2: 8 x + 12 y = 72 ...... (3)
=3 (3) − (1) :
∴ The solution is x = 3, y = −1.
8 x + 12 y = 72
−) 3 x + 12 y = 33
2.  4x 3y
 − = 1 ...... (1)
5 5 5 x = 39
5 x − 2 y = 15 ...... (2)
 x = 7.8
From (1), we have By substituting x = 7.8 into (2), we have
4x − 3y = 5 4(7.8) + 6 y = 36
4x = 3y + 5 31.2 + 6 y = 36
3 5 6 y = 4.8
x = y + ...... (3)
4 4 y = 0.8
By substituting (3) into (2), we have Cost of 1 bottle of milk and 2 eggs = $(7.8 × 1 + 0.8 × 2)
3 5
5 y +  − 2 y = 15 = $9.4
 4 4 ∴ The man should pay $9.4.
15 25
y+ − 2 y = 15
4 4 5. (a) 7 + 7 −4 × 7 0 × 7 4 = 7 + 7 −4 + 0 + 4
7 35 = 7 + 70
y=
4 4
= 7 +1
y=5
=8
By substituting y = 5 into (3), we have
3 5
x = (5) + = 5
4 4 (b) (2 p −1 )3 × (3 p 4 ) −3 = 23 p −1×3 × 3−3 p 4× ( −3)
∴ The solution is x = 5, y = 5. 8 1
= ×
p 3 27 p12
3. 2 x + y + 1 = 0 8
 =
x − 2 y + 8 = 0 27 p 3 +12
x − 2y + 8 = 0 8
=
x –4 0 2 27 p15
y 2 4 5
By adding the line x − 2 y + 8 = 0 on the graph, we have (5 × 1014 ) × (5.4 ×10 −9 ) 5 × 5.4
6. = ×1014 + ( −9) − ( −6)
3.6 × 10− 6 3.6
= 7.5 × 1011
139

2. Math in Action (2nd Edition) 2B Full Solutions
7. C5E216 = 12 ×163 + 5 × 162 + 14 × 161 + 2 × 160 By substituting C = 40 into (3), we have
B = 9000 − 100(40)
8. Consider ABE and ACD. = 5000
AB = AC sides opp. equal ∠s ∴ The solution is B = 5000, C = 40.
∠B = ∠C given
(b) The salesman’s salary in that month
∠BAE = ∠BAD + ∠DAE
= $(5000 + 40 × 250)
= ∠CAE + ∠DAE given
= $15 000
= ∠CAD
∴ ∠BAE = ∠CAD
13. (a) Original number = 10y + x
∴ ABE ≅ ACD ASA
New number = 10x + y
9. In PAD,
(b) (i) From the question, we have
90° + ∠PDA = ∠DAQ ext. ∠ of
x + y = 8
= 90° + ∠QAB 
∴ ∠PDA = ∠QAB (10 y + x) − (10 x + y ) = 18
After simplification, we have
Consider DPA and AQB.
∠DPA = ∠AQB = 90° given x + y = 8

∠PDA = ∠QAB proved − x + y = 2
∴ DPA ~ AQB AAA
(ii)  x + y = 8 ...... (1)

− x + y = 2 ...... (2)
10. (a) In ABC,
∠CAB = ∠CBA base ∠s, isos.
(1) + (2) :
∴ ∠CAD = ∠CBE
Consider ACD and BCE. x+ y =8
AD = BE given +) − x + y = 2
AC = BC given 2 y = 10
∠CAD = ∠CBE proved y =5
∴ ACD ≅ BCE SAS
By substituting y = 5 into (1), we have
∴ DC = EC corr. sides, ≅ s
x+5=8
(b) ∵ ACD ≅ BCE proved in (a) x=3
∴ ∠ACD = ∠BCE corr. ∠s, ≅ s ∴ The original number is 53.
∠DCB = ∠ACD + ∠ACB
14. (a) The place value of 0 in 110111112 = 25
= ∠BCE + ∠ACB corr. ∠s, ≅ s
= ∠ECA The place value of 0 in 1B016 = 160
11. (a) In ABC, (b) 110111112
∵ AB = AC given
= 1× 2 7 + 1× 2 6 + 0 × 2 5 + 1 × 2 4 + 1× 2 3
∴ ∠B = ∠C base ∠s, isos.
Consider LBM and HCK. + 1× 2 2 + 1× 21 + 1× 2 0
BM = CK given = 128 + 64 + 0 + 16 + 8 + 4 + 2 + 1
∠B = ∠C proved = 22310
∠BML = ∠CKH = 90° given
∴ LBM ≅ HCK ASA
1B016 = 1×16 2 + 11×161 + 0 × 16 0
(b) Consider LMK and HKM. = 256 + 176 + 0
MK = KM common side = 43210
∠LMK = ∠HKM = 90° given
LM = HK corr. sides, ≅ s
∴ LMK ≅ HKM SAS (c) Arranging 110111112, 1B016 and 30010 in descending
order, we have
1B016 > 30010 > 110111112
Part B
12. (a) From the question, we have
15. (a) 6 x −1 6 1
B + 100C = 9000 ...... (1) (3 xy 3 ) −1 = ×
 x0 y xy 3 xy 3
B + 400C = 21 000 ...... ( 2) 2
From (1), we have = 2 4
x y
B = 9000 − 100C ...... (3)
By substituting (3) into (2), we have
(9000 − 100C ) + 400C = 21 000 (b) (i) 4 2 x −1 = 2 2( 2 x −1)
300C = 12 000
C = 40
140

3. Integrated Exercise A
8−2 = ( 23 ) −2 (c) ∵ ACD ~ ABC proved in (a)
CBD ~ ACD proved in (b)
= 2− 6 ∴ ABC ~ CBD
1 1 AB BC
= ∴ = corr. sides, ~ △s
16 2 4 CB BD
= 2− 4 BC 2 = BD × AB
18. (a)
4 2 x −1 (8−2 )
(ii) = 2 2( 2 x −1) × 2− 6 × 2 − 4
16
= 24 x − 2− 6− 4
= 2 4 x −12
= 2 4 ( x − 3)
16. (a) ∠BAD + ∠ABC = 180° int. ∠s, AD // BC
∠ADC + ∠DCB = 180° int. ∠s, AD // BC
∵ ∠ABC = ∠DCB given
∴ ∠BAD = ∠CDA
Consider ABD and DCA. ∵ ∠COB = 90°
AB = DC given ∠EOB = 45°
AD = DA common side ∠BOF = 60°
∠BAD = ∠CDA proved ∴ ∠EOF = ∠EOB + ∠BOF
∴ ABD ≅ DCA SAS = 45° + 60°
= 105°
(b) ∵ ABD ≅ DCA proved in (a)
1
∴ ∠ABD = ∠DCA corr. ∠s, ≅ s ∠GOF = × 105°
2
∴ ∠CBD = ∠BCA
= 52.5°
∴ OC = OB sides opp. equal ∠s
∴ OBC is an isosceles triangle.
(b)
17. (a) (i) Consider ACD and ABC.
∠A = ∠A common angle
∠ADC = ∠ACB = 90° given
∴ ACD ~ ABC AAA
(ii) ∵ ACD ~ ABC proved in (a)(i)
AC AD
∴ = corr. sides, ~ △s
AB AC
AC 2 = AD × AB
(b) (i) Consider BCD and CAD.
Multiple Choice Questions
1. Answer: B
∵ b = 180° − a − 90° ∠ sum of
= 90° − a 3 x − 2 y = 7 ...... (1)

c1 = 180° − a − 90° ∠ sum of 5 x + 2 y = 1 ...... (2)
= 90° − a (1) + (2) :
∴ b = c1 3x − 2 y = 7
∠ADC = ∠CDB = 90° given +) 5 x + 2 y = 1
∴ BCD ~ CAD AAA
8x = 8
(ii) ∵ △BCD ~ △CAD provided in (b)(i) x =1
CD DB By substituting x = 1 into (2), we have
∴ = corr. sides, ~ △s 5(1) + 2 y = 1
AD DC
CD 2 = AD × BD 2 y = −4
y = −2
∴ The solution is x = 1, y = −2.
141

4. Math in Action (2nd Edition) 2B Full Solutions
2. Answer: C
Point R is the point of intersection of the graphs.
3. Answer: D
2 x + 3 y = 6 ...... (1)

bx + y = 7 ...... (2)
By substituting x = a and y = 4 into (1), we have
2a + 3(4) = 6
2a = −6
a = −3
By substituting x = −3 and y = 4 into (2), we have
−3b + 4 = 7
− 3b = 3
b = −1
∴ The solution is a = −3, b = −1.
4. Answer: D
5. Answer: B
5 4 + 54 + 54 + 5 4 + 5 4 = 5 × 54
= 51+ 4
= 55
6. Answer: C
7. Answer: B
8. Answer: A
9. Answer: B
10. Answer: C
AAS
142