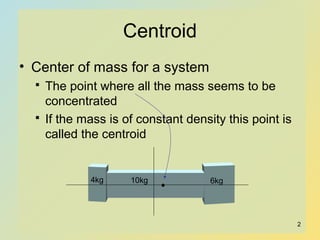
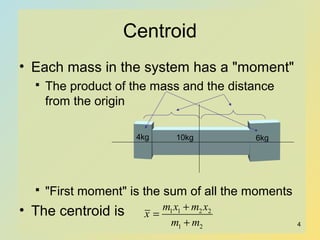
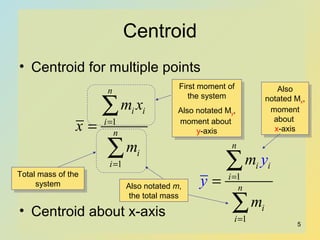
The document discusses centroids, which are the centers of mass for systems. The centroid of an area is analogous to the center of gravity of a body. To find the centroid, you calculate the first moment of the system, which is the sum of the products of each mass and its distance from the origin. You can find the centroid of multiple points by dividing the first moment about each axis by the total mass of the system. The document provides an example of calculating the centroid of a system with masses located at different coordinate points. It also discusses finding centroids of common geometric shapes.

1. Centroids
BY
Usman Sajid Sohrani

2. 2
Centroid
• Center of mass for a system
 The point where all the mass seems to be
concentrated
 If the mass is of constant density this point is
called the centroid
4kg 6kg10kg
•

3. • The centroid of an area is analogous to the
center of gravity of a body. The concept of the
first moment of an area is used to locate the
centroid.
3

4. 4
Centroid
• Each mass in the system has a "moment"
 The product of the mass and the distance
from the origin
 "First moment" is the sum of all the moments
• The centroid is
4kg 6kg10kg
1 1 2 2
1 2
m x m x
x
m m
+
=
+

5. 5
Centroid
• Centroid for multiple points
• Centroid about x-axis
1
1
n
i i
i
n
i
i
m x
x
m
=
=
=
∑
∑
First moment of
the system
Also notated My,
moment about
y-axis
First moment of
the system
Also notated My,
moment about
y-axis
Total mass of the
system
Total mass of the
system
1
1
n
i i
i
n
i
i
y
y
m
m
=
=
=
∑
∑
Also
notated Mx,
moment
about
x-axis
Also
notated Mx,
moment
about
x-axis
Also notated m,
the total mass

6. 6
Centroid
• The location of the centroid is the ordered
pair
• Consider a system with 10g at (2,-1), 7g at
(4, 3), and 12g at (-5,2)
 What is the center of mass?
( , )x y
y x
M M
x y
m m
= =

7. 7
Centroid
• Given 10g at (2,-1), 7g at (4, 3), and 12g
at (-5,2)
10g
7g
12g
10 (2) 7 4 12 ( 5)
10 ( 1) 7 3 12 2
10 7 12
y
x
M
M
m
= × + × + × −
= × − + × + ×
= + + ? ?x y= =

8. Centroids of Common Shapes of Areas
8

9. 9
Sample Problem 5.1
For the plane area shown, determine
the first moments with respect to the
x and y axes and the location of the
centroid.
SOLUTION:
• Divide the area into a triangle, rectangle,
and semicircle with a circular cutout.
• Compute the coordinates of the area
centroid by dividing the first moments by
the total area.
• Find the total area and first moments of
the triangle, rectangle, and semicircle.
Subtract the area and first moment of the
circular cutout.
• Calculate the first moments of each area
with respect to the axes.

10. 10
Sample Problem 5.1
33
33
mm107.757
mm102.506
×+=
×+=
y
x
Q
Q• Find the total area and first moments of the
triangle, rectangle, and semicircle. Subtract the
area and first moment of the circular cutout.

11. 5 - 11
Sample Problem 5.1
23
33
mm1013.828
mm107.757
×
×+
==
∑
∑
A
Ax
X
mm8.54=X
23
33
mm1013.828
mm102.506
×
×+
==
∑
∑
A
Ay
Y
mm6.36=Y
• Compute the coordinates of the area
centroid by dividing the first moments by
the total area.