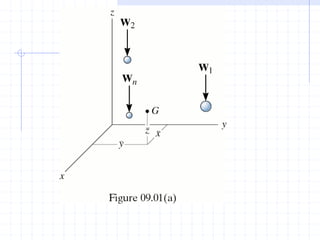
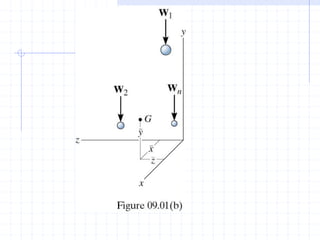
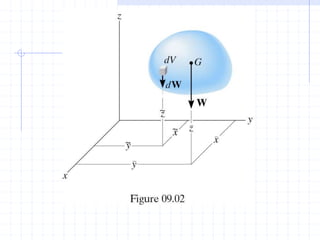
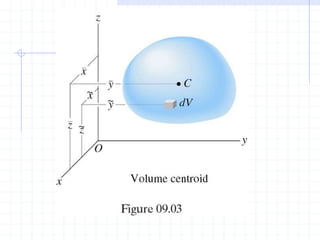
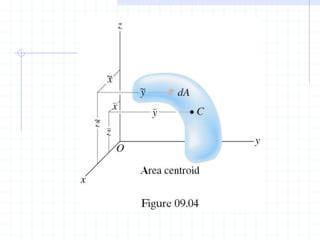
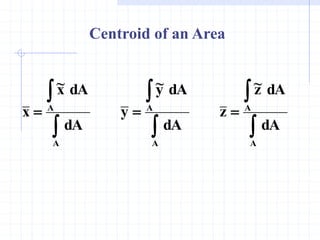
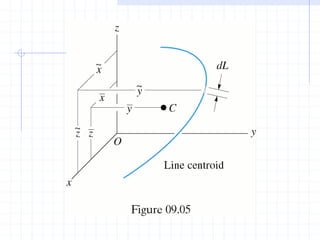
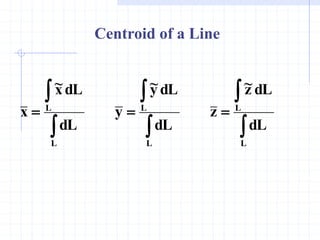
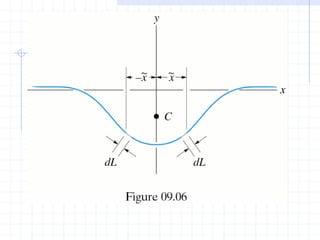
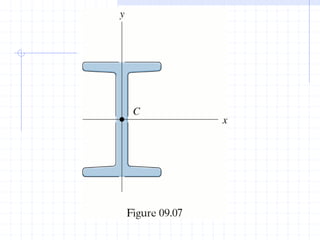
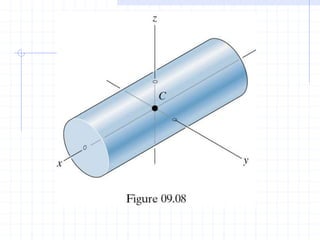
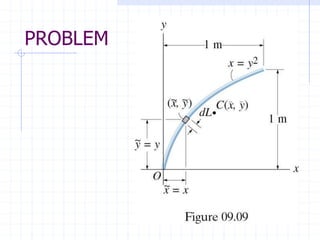
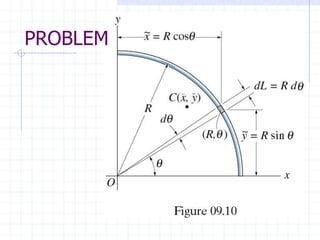
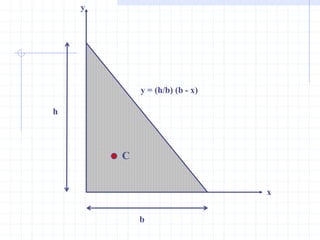
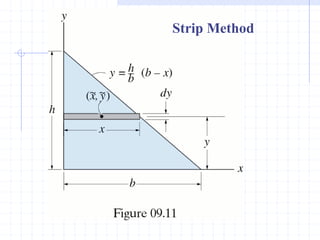
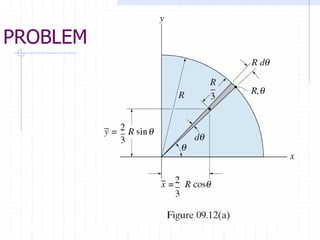
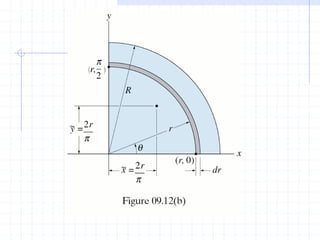
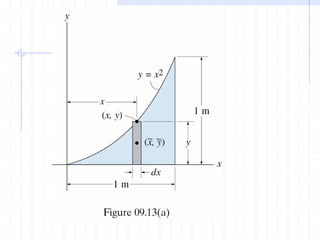
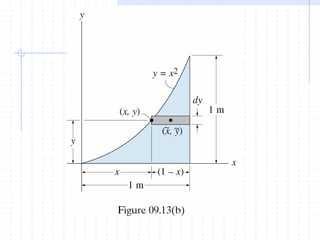
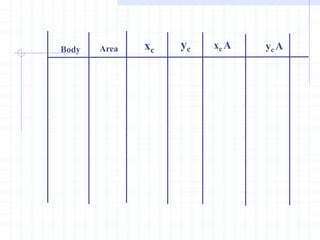
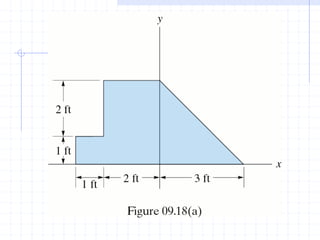
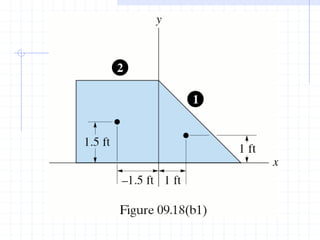
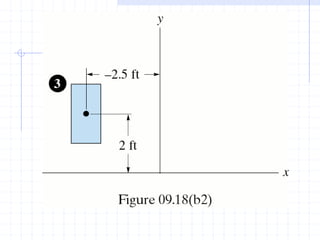
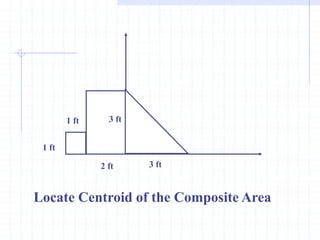
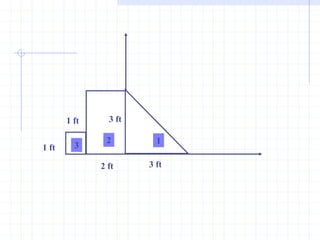
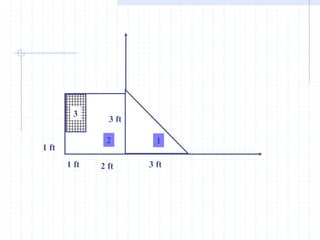
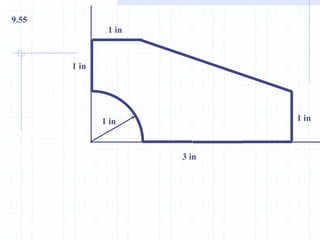
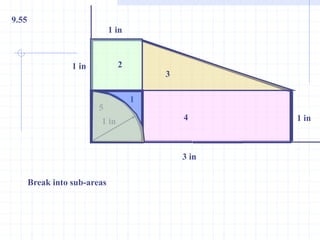
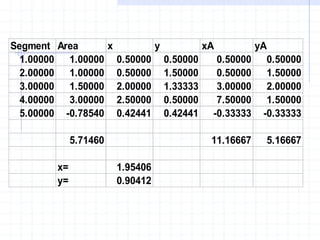
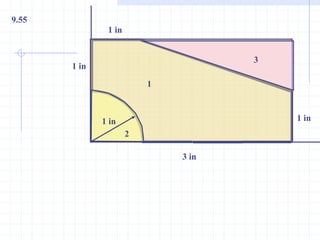
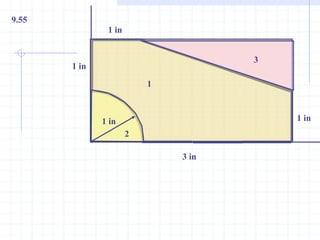
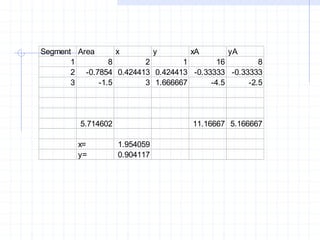
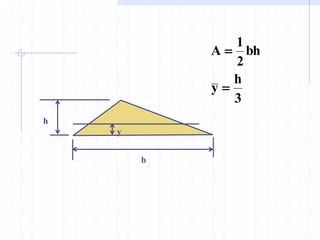
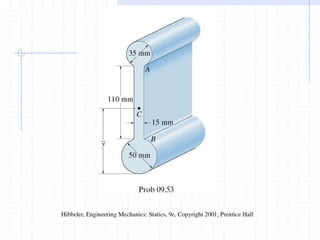
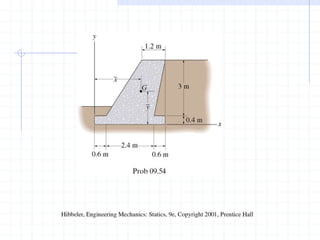
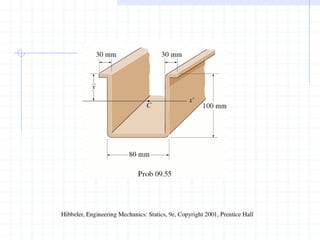
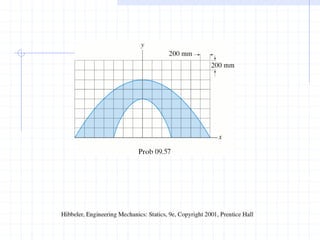
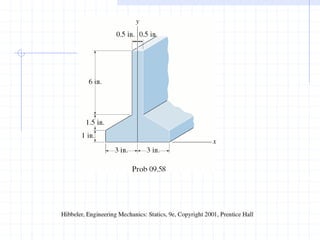
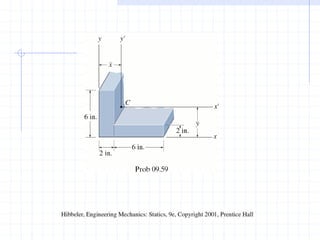
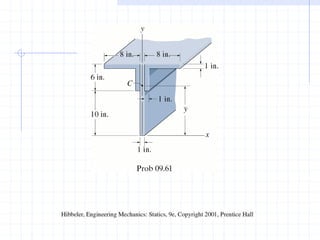
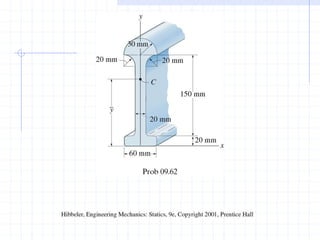
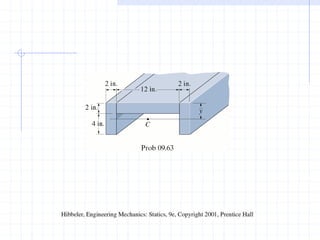
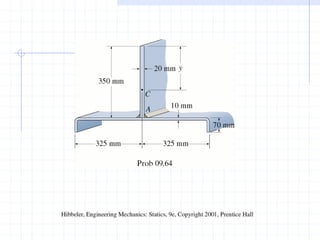
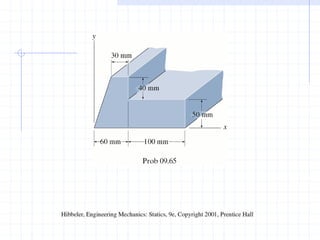
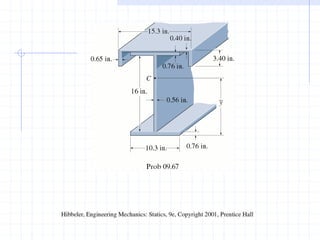
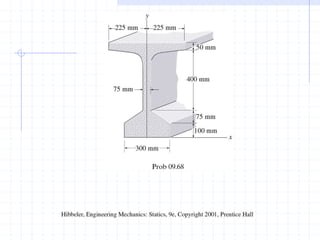
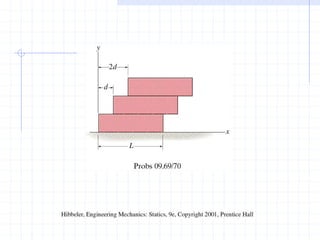
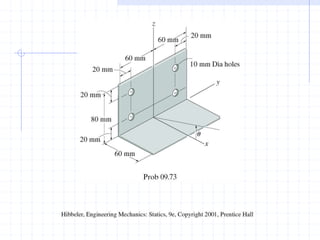
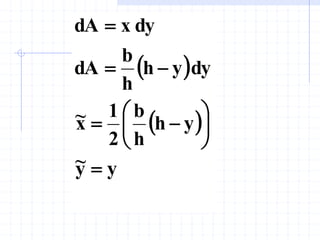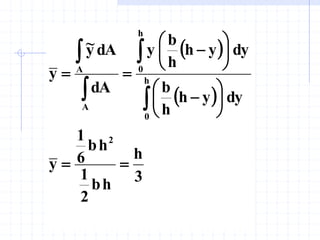This document discusses concepts related to centers of gravity, mass, and area (centroids). It defines the center of gravity as the point where the total weight of a system of particles can be considered to act. Formulas are provided to calculate the x, y, and z coordinates of the center of gravity for discrete particles and continuous bodies. Similarly, the centroid is defined as the geometric center of an object and its location can be determined through integrals over dimensions like area, volume, or length. Several example problems are worked through to demonstrate calculating centroids of composite shapes by dividing them into subareas.

1. Objectives
To discuss the concept of the center of
gravity, center of mass, and centroids
(centers of area).
To show how to determine the location
of the center of gravity and centroid for
a system of particles and a body of
arbitrary shape.

2. Center of Gravity
The center of gravity G is a point which locates the
resultant weight of a system of particles.
The weights of the particles is considered to be a
parallel force system. The system of weights can be
replaced by a single weight acting at the Center of
Gravity.

5. 


n
1
i
i
R W
W Total Weight
n
n
3
3
2
2
1
1
R
R W
x
~
W
x
~
W
x
~
W
x
~
W
x 




x location:
n
n
3
3
2
2
1
1
R
R W
y
~
W
y
~
W
y
~
W
y
~
W
y 




y location:
n
n
3
3
2
2
1
1
R
R W
z
~
W
z
~
W
z
~
W
z
~
W
z 




z location:

6. 













 n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
W
W
z
~
z
W
W
y
~
y
W
W
x
~
x
particle
i
the
of
weight
W
particle
i
the
of
s
coordinate
z
~
,
y
~
,
x
~
gravity
of
center
the
of
s
coordinate
z
,
y
,
x
th
i
th
i
i
i

7. 













 n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
m
m
z
~
z
m
m
y
~
y
m
m
x
~
x
particle
i
the
of
mass
W
particle
i
the
of
s
coordinate
z
~
,
y
~
,
x
~
mass
of
center
the
of
s
coordinate
z
,
y
,
x
th
i
th
i
i
i
Center of Mass

8. Center of Gravity and Centroid
for a Body
Consider a body to be a system of
an infinite number of particles

10. 




















1
i
i
i
1
i
i
1
i
i
i
1
i
i
1
i
i
i
1
i
i
W
W
z
~
z
W
W
y
~
y
W
W
x
~
x
particle
i
the
of
weight
W
particle
i
the
of
s
coordinate
z
~
,
y
~
,
x
~
gravity
of
center
the
of
s
coordinate
z
,
y
,
x
th
i
th
i
i
i

11. 




 


dW
dW
z
~
z
dW
dW
y
~
y
dW
dW
x
~
x
 
V
d
W
d
body
the
of
weight
specific




volume
unit
per
The weight

12. 














V
V
V
V
V
V
dV
dV
z
~
z
dV
dV
y
~
y
dV
dV
x
~
x
Center of Gravity of a Body

13. CENTROID
The centroid C is a point which defines the
geometric center of an object. Its location can
be determined by formulas similar to those
used for center of gravity or center of mass.

15. 








V
V
V
V
V
V
dV
dV
z
~
z
dV
dV
y
~
y
dV
dV
x
~
x
Centroid of a Volume

17. 








A
A
A
A
A
A
dA
dA
z
~
z
dA
dA
y
~
y
dA
dA
x
~
x
Centroid of an Area

19. 








L
L
L
L
L
L
dL
dL
z
~
z
dL
dL
y
~
y
dL
dL
x
~
x
Centroid of a Line

24. PROBLEM

25.    
  dy
1
y
2
dL
y
2
dy
dx
y
x
dy
1
dy
dx
dL
dy
dx
dL
2
2
2
2
2





 


























26.  
 
 
 
m
410
.
0
479
.
1
6063
.
0
dy
1
y
4
dy
1
y
4
y
x
y
x
dy
1
y
2
dy
1
y
2
x
dL
dL
x
~
x
1
0
2
1
0
2
2
2
1
0
2
1
0
2
L
L











 





 









27.  
 
 
 
m
574
.
0
479
.
1
8484
.
0
dy
1
y
4
dy
1
y
4
y
y
dy
1
y
2
dy
1
y
2
y
dL
dL
y
~
y
1
0
2
1
0
2
1
0
2
1
0
2
L
L










 





 









28. PROBLEM

29.  
 
2 2
2 2
2 2
2 2
2
0 0
L
L
0 0
2
0 0
L
L
0 0
Rcos Rd R cos d
xdL
2R
x
dL
Rd R d
Rsin Rd R sin d
ydL
2R
y
dL
Rd R d
 
 
 
 
   
   

 
   
   

 
 


 
 


 

30. y
x
b
h
y = (h/b) (b - x)
C

31. Strip Method

32.  
 
y
y
~
y
h
h
b
2
1
x
~
dy
y
h
h
b
dA
dy
x
dA













33.  
 
3
h
h
b
2
1
h
b
6
1
y
dy
y
h
h
b
dy
y
h
h
b
y
dA
dA
y
~
y
2
h
0
h
0
A
A























34.    
 
h
0
A
h
A
0
2
1 b b
h y h y dy
x dA
2 h h
x
b
dA
h y dy
h
1
b h
b
6
x
1 3
b h
2
  
 
  
  
 
 

 
 
 


 

35. PROBLEM

39. Composite Bodies

40. Composite Bodies
If a body is made up of several simpler
bodies then a special technique can be used.

41. Procedure
Divide body into several subparts.
If the body has a hole or cutout, treat
that as negative area.
Centroid will lie on line of symmetry.
Create Table and calculate centroid.

42. 













 n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
n
1
i
i
i
n
1
i
i
A
A
z
~
z
A
A
y
~
y
A
A
x
~
x
particle
i
the
of
weight
W
particle
i
the
of
s
coordinate
z
~
,
y
~
,
x
~
gravity
of
center
the
of
s
coordinate
z
,
y
,
x
th
i
th
i
i
i

43. Area
Body xc yc xc A yc A

47. 1 ft
1 ft
2 ft 3 ft
3 ft
Locate Centroid of the Composite Area

48. 1 ft
1 ft
2 ft 3 ft
3 ft
1
2
3

49. Segment A (ft2) x y xA yA
1 4.5 1 1 4.5 4.5
2 6 -1 1.5 -6 9
3 1 -2.5 0.5 -2.5 0.5
 A = 11.5  xA = -4  xA = 14
ft
22
.
1
5
.
11
14
A
A
y
~
y
ft
348
.
0
5
.
11
4
A
A
x
~
x













50. 1 ft
1 ft 2 ft 3 ft
3 ft
1
2
3

51. Segement A (ft2) x y xA yA
1 4.5 1 1 4.5 4.5
2 9 -1.5 1.5 -13.5 13.5
3 -2.5 -2.5 2 5 -4
 A = 11.5  xA = -4  xA = 14
ft
22
.
1
5
.
11
14
A
A
y
~
y
ft
348
.
0
5
.
11
4
A
A
x
~
x













52. 9.55
1 in
3 in
1 in
1 in
1 in

53. 9.55
1 in
3 in
1 in
1 in
1 in
1
2
3
4
5
Break into sub-areas

54. Segment Area x y xA yA
1.00000 1.00000 0.50000 0.50000 0.50000 0.50000
2.00000 1.00000 0.50000 1.50000 0.50000 1.50000
3.00000 1.50000 2.00000 1.33333 3.00000 2.00000
4.00000 3.00000 2.50000 0.50000 7.50000 1.50000
5.00000 -0.78540 0.42441 0.42441 -0.33333 -0.33333
5.71460 11.16667 5.16667
x= 1.95406
y= 0.90412

55. 9.55
3 in
1 in
1 in
1 in
1
3
2
1 in

56. 9.55
3 in
1 in
1 in
1 in
1
3
2
1 in

57. 9.55
3 in
1 in
1 in
1 in
1
3
2
1 in

58. Segment Area x y xA yA
1 8 2 1 16 8
2 -0.7854 0.424413 0.424413 -0.33333 -0.33333
3 -1.5 3 1.666667 -4.5 -2.5
5.714602 11.16667 5.166667
x= 1.954059
y= 0.904117

59. h
b
3
h
y
bh
2
1
A


y