Download to read offline
![[PRML] パターン認識と機械学習（第1章：序論）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter1-170903070406-thumbnail.jpg?width=640&height=640&fit=bounds)
![[PRML] パターン認識と機械学習（第3章：線形回帰モデル）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter3-171003081954-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL Hacks] Deterministic Variational Inference for RobustBayesian Neural Netw...](https://cdn.slidesharecdn.com/ss_thumbnails/adobepdffile2-190628001736-thumbnail.jpg?width=640&height=640&fit=bounds)
Statistical machine learning
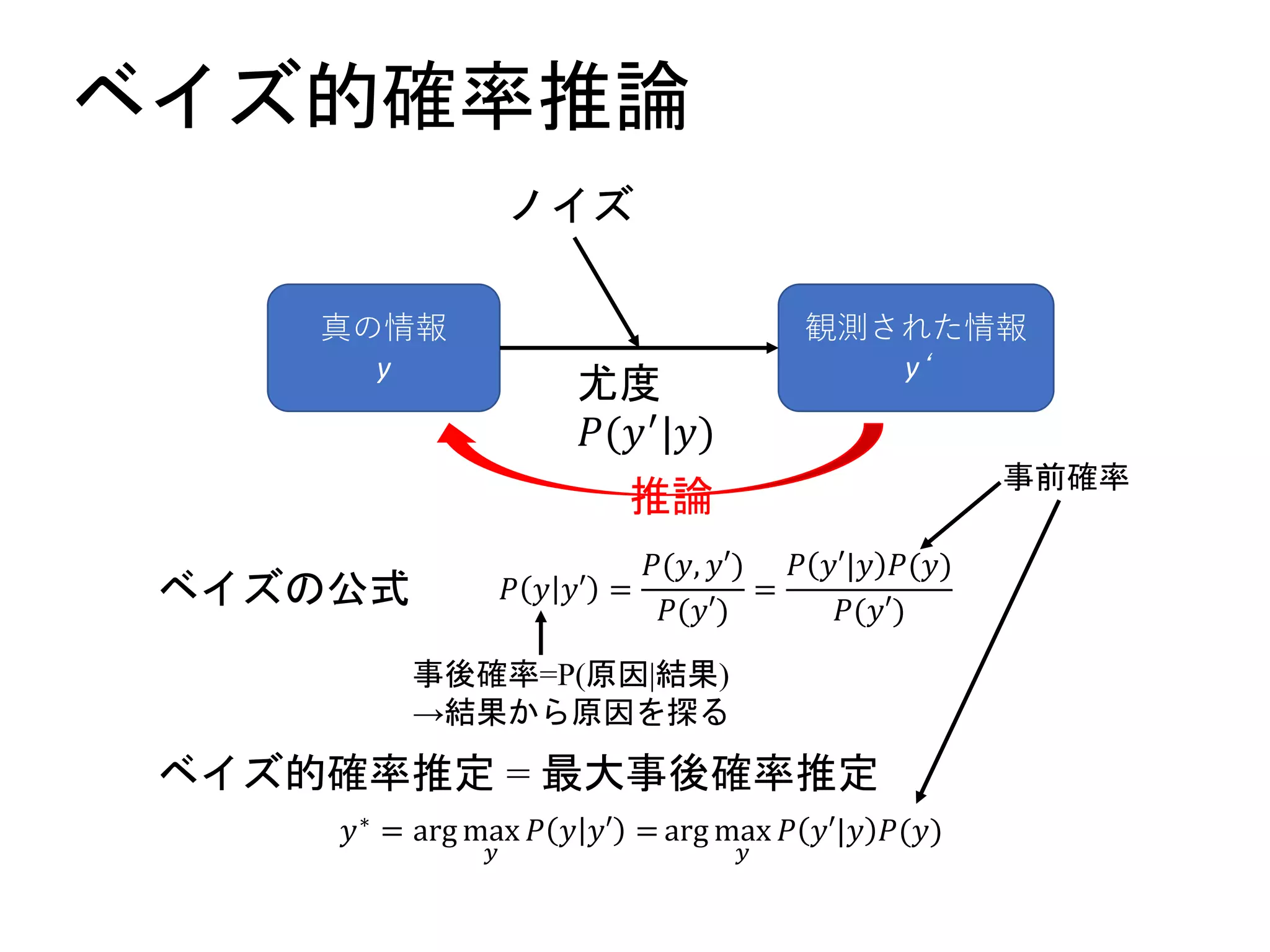
- 1.
- 2.
- 3.
- 4. ベイズ的確率推論 真の情報 y 観測された情報 y‘ ノイズ 尤度 𝑃(𝑦′|𝑦) 推論 ベイズの公式 𝑃 𝑦𝑦′ = 𝑃(𝑦, 𝑦′) 𝑃(𝑦′) = 𝑃 𝑦′|𝑦 𝑃(𝑦) 𝑃(𝑦′) 事後確率=P(原因|結果) →結果から原因を探る ベイズ的確率推定 = 最大事後確率推定 𝑦∗ = arg max 𝑦 𝑃 𝑦 𝑦′ = arg max 𝑦 𝑃 𝑦′|𝑦 𝑃(𝑦) 事前確率
- 5.
- 6. 統計的機械学習 真の情報 y 観測された情報 y‘ 生成 学習推定 学習モデル 𝑃 𝑦|𝜃 観測データ𝑦′から仮定した学習モデルを学習 →未知の事前確率に学習モデルを近づける 𝑦∗ = arg max 𝑦 𝑃 𝑦|𝑦′ 𝑃(𝑦′) ~arg max 𝑦 𝑃 𝑦|𝑦′ 𝑃 𝑦|𝜃 どのようなモデルを仮定すればいいか →グラフィカルモデル
- 7.
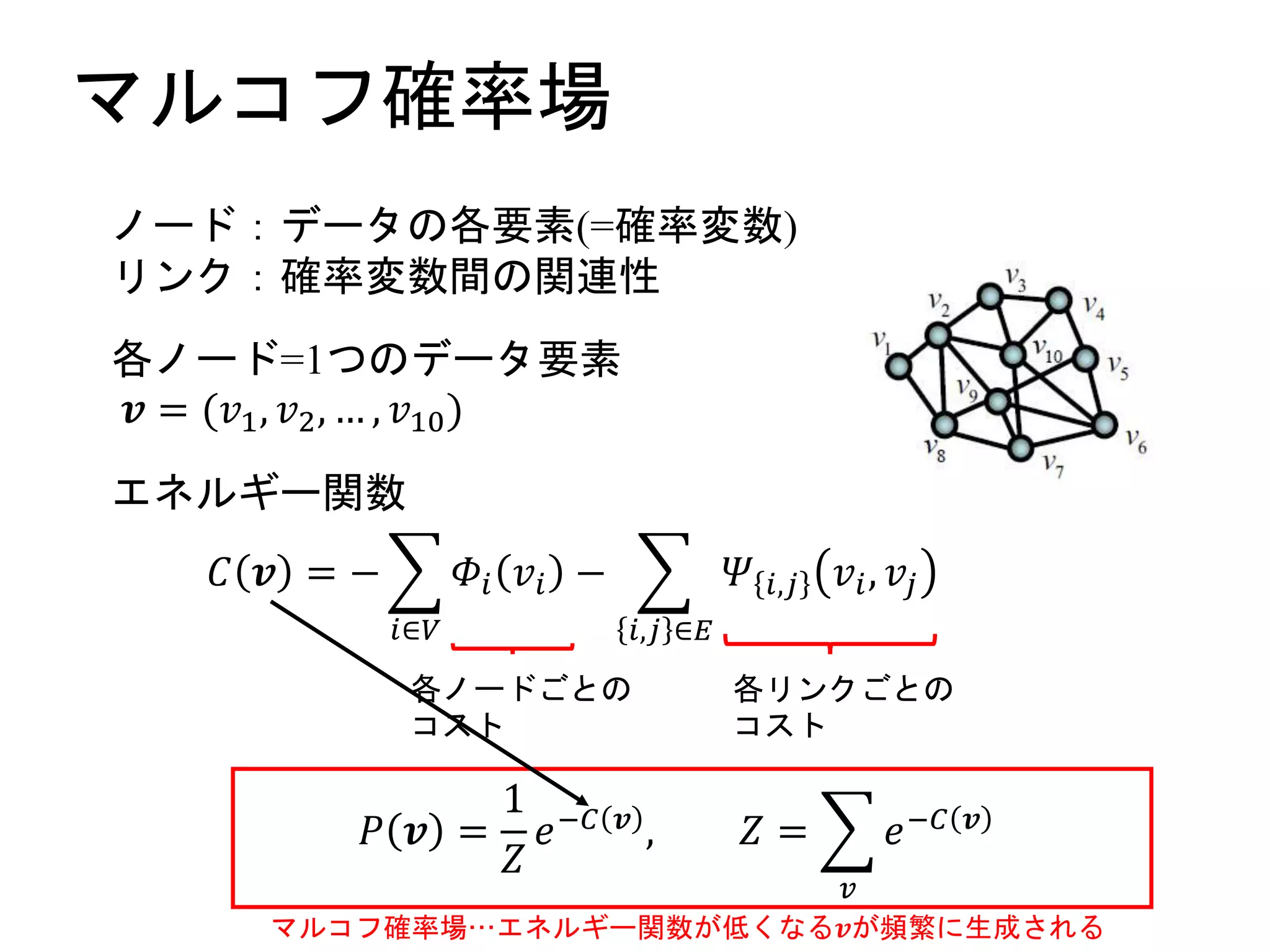
- 8. マルコフ確率場 エネルギー関数 𝐶 𝒗 =− 𝑖∈𝑉 𝛷𝑖 𝑣𝑖 − 𝑖,𝑗 ∈𝐸 𝛹 𝑖,𝑗 𝑣𝑖, 𝑣𝑗 各ノードごとの コスト 各リンクごとの コスト 𝑃 𝒗 = 1 𝑍 𝑒−𝐶 𝒗 , 𝑍 = 𝑣 𝑒−𝐶 𝒗 マルコフ確率場…エネルギー関数が低くなる𝒗が頻繁に生成される ノード：データの各要素(=確率変数) リンク：確率変数間の関連性 各ノード=1つのデータ要素 𝒗 = (𝑣1, 𝑣2, … , 𝑣10)
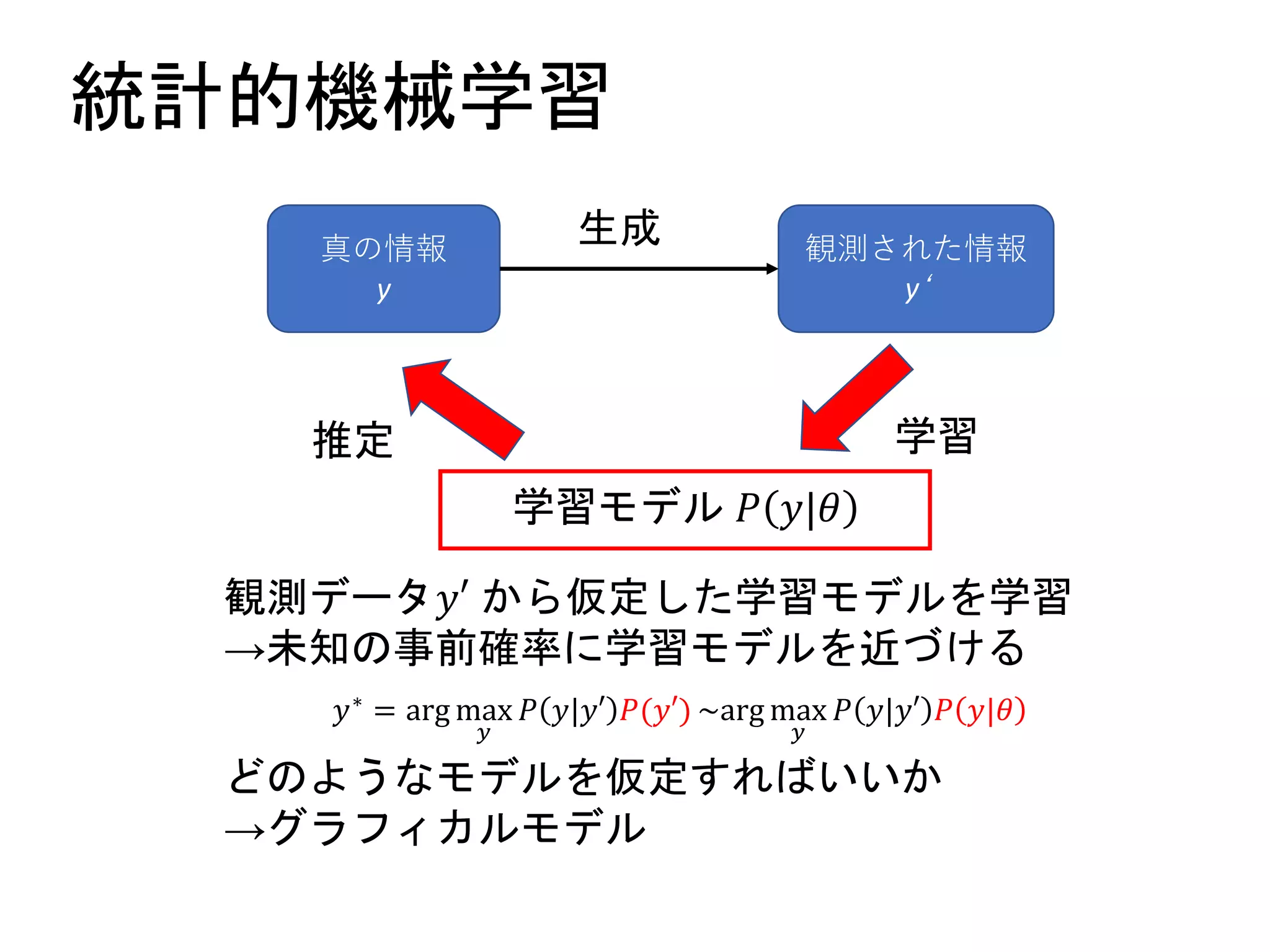
- 9. ボルツマンマシン Boltzmann Machine ・最も基本的なマルコフ確率場 ・相互結合型の確率的ニューラルネットワーク 𝛷𝑖𝑣𝑖 = 𝑏𝑖 𝑣𝑖 𝛹 𝑖,𝑗 𝑣𝑖, 𝑣𝑗 = 𝑤𝑖𝑗 𝑣𝑖 𝑣𝑗 と仮定して、 𝐶 𝒗 = − 𝑖∈𝑉 𝑏𝑖 𝑣𝑖 − 𝑖,𝑗 ∈𝐸 𝑤𝑖𝑗 𝑣𝑖 𝑣𝑗 𝑣𝑖 ∈ 0,1 ノードi のバイアス値 リンク(i,j) のパラメター →変数同士の複雑な関連性
- 10.
- 11. 最尤推定(maximum likelihood estimation,MLE) 観測データ D 生成？ ボルツマンマシン𝑃 𝒚|𝜽 ・観測データDは学習モデルBMから、独立に同じ分布 (i.i.d.)で生成されたと考える。 ※近似。実際は事前確率から生成 ・観測データ生成に対し尤もらしい確率になるように パラメターθを調整 𝑏𝑖, 𝑤𝑖𝑗
- 12. 最尤推定(maximum likelihood estimation,MLE) 𝐷 = 𝒅(1), 𝒅(2), … , 𝒅(𝑁) , 𝒅(𝜇) = 𝑑1 (𝜇) , 𝑑2 (𝜇) , … , 𝑑 𝑛 (𝜇) として、観測データと同じn次元の変数を持つBM 𝑃 𝒚|𝜽 𝒚 = 𝑣1, 𝑣2, … , 𝑣 𝑛 を作成すると、観測データ群Dを生成する確率は、 𝑃 𝒚 = 𝒅 1 𝜽 𝑃 𝒚 = 𝒅 2 𝜽 … 𝑃 𝒚 = 𝒅 𝑁 𝜽 ※各データ𝒅(𝜇) は独立に生成される ・尤度関数=仮定した学習モデルが実際に観測データを 生成する確率 →観測データに対して一番尤もらしいモデル=尤度関数 を最大とするパラメター値の時のモデル →これを求めるのが最尤推定 =尤度関数
- 13. 最尤推定(maximum likelihood estimation,MLE) の最大点は、対数 𝜇=1 𝑁 𝑙𝑛𝑃 𝒚 = 𝒅 𝜇 𝜽 𝑃 𝒚 = 𝒅 1 𝜽 𝑃 𝒚 = 𝒅 2 𝜽 … 𝑃 𝒚 = 𝒅 𝑁 𝜽 の最大点に一致する(←尤度関数が単調増加)。 =対数尤度関数
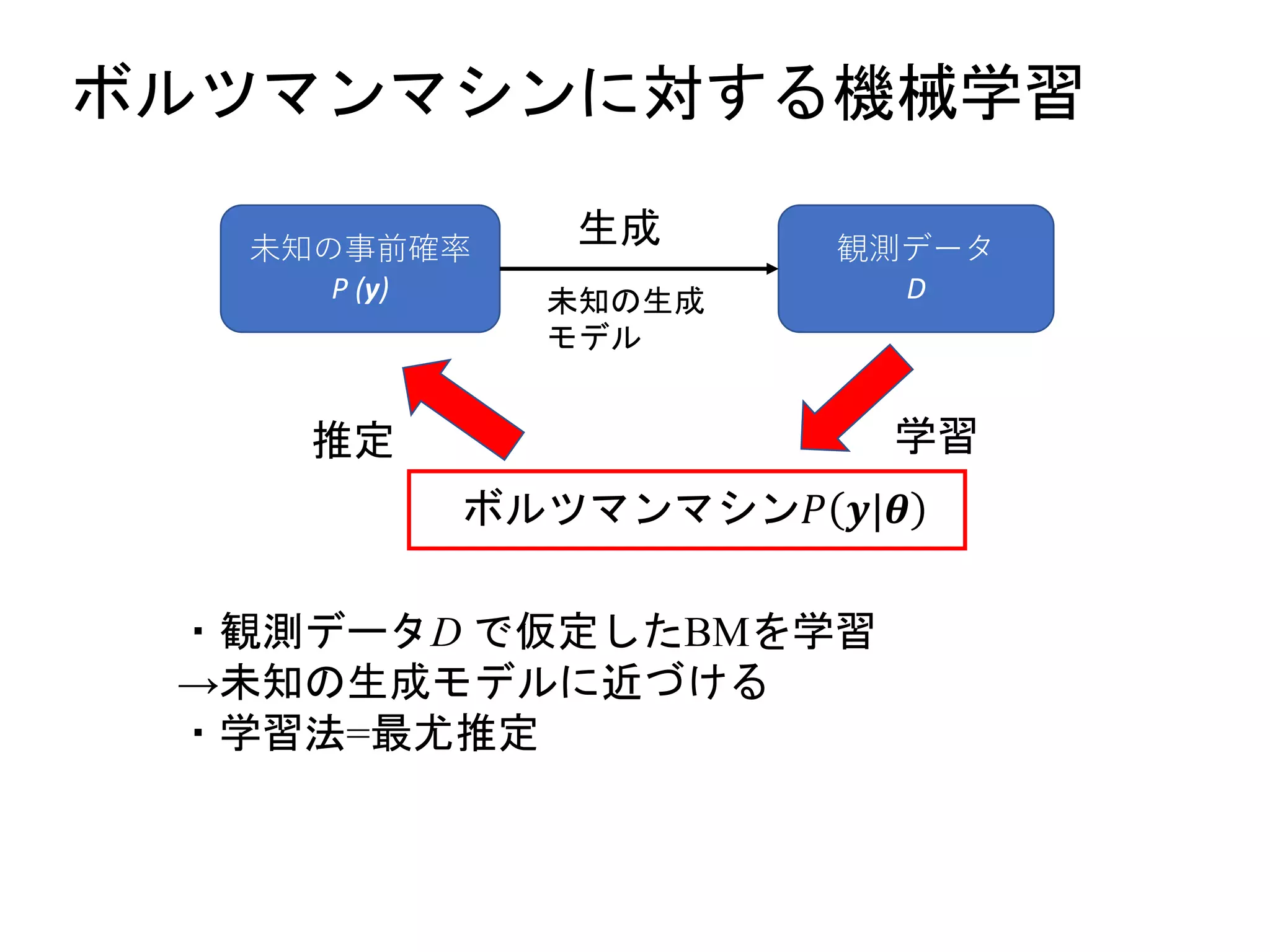
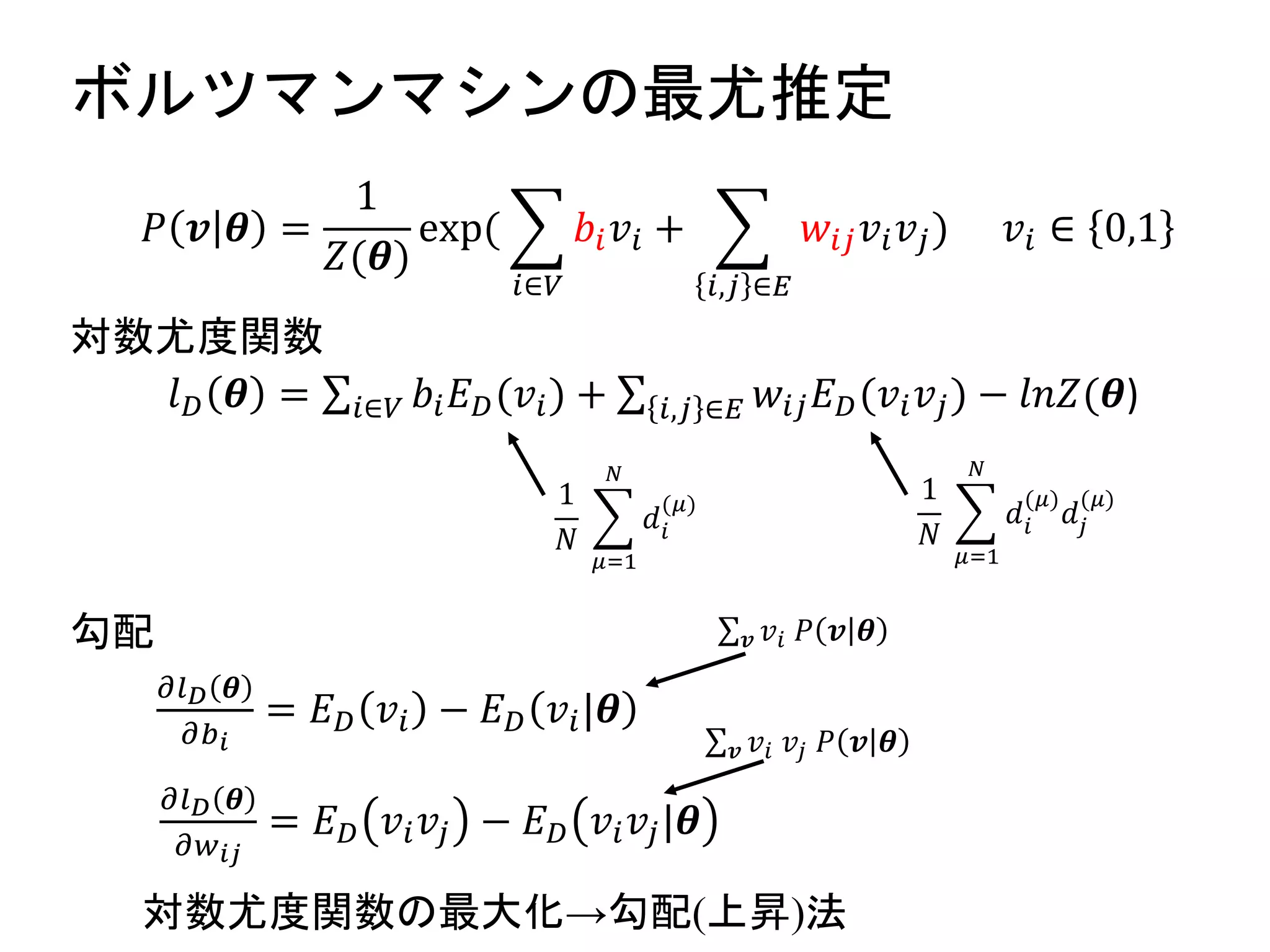
- 14. ボルツマンマシンの最尤推定 𝑙 𝐷 𝜽= 𝑖∈𝑉 𝑏𝑖 𝐸 𝐷(𝑣𝑖) + 𝑖,𝑗 ∈𝐸 𝑤𝑖𝑗 𝐸 𝐷(𝑣𝑖 𝑣𝑗) − 𝑙𝑛𝑍(𝜽) 𝑃 𝒗 𝜽 = 1 𝑍(𝜽) exp( 𝑖∈𝑉 𝑏𝑖 𝑣𝑖 + 𝑖,𝑗 ∈𝐸 𝑤𝑖𝑗 𝑣𝑖 𝑣𝑗) 𝑣𝑖 ∈ 0,1 勾配 対数尤度関数 1 𝑁 𝜇=1 𝑁 𝑑𝑖 (𝜇) 1 𝑁 𝜇=1 𝑁 𝑑𝑖 (𝜇) 𝑑𝑗 (𝜇) 𝜕𝑙 𝐷 𝜽 𝜕𝑏 𝑖 = 𝐸 𝐷 𝑣𝑖 − 𝐸 𝐷 𝑣𝑖|𝜽 𝜕𝑙 𝐷 𝜽 𝜕𝑤 𝑖𝑗 = 𝐸 𝐷 𝑣𝑖 𝑣𝑗 − 𝐸 𝐷 𝑣𝑖 𝑣𝑗|𝜽 𝒗 𝑣𝑖 𝑃 𝒗 𝜽 𝒗 𝑣𝑖 𝑣𝑗 𝑃 𝒗 𝜽 対数尤度関数の最大化→勾配(上昇)法
- 15. 勾配上昇法 𝑥 𝑛𝑒𝑤 ←𝑥 𝑜𝑙𝑑 + 𝜀 𝜕𝑓(𝑥 𝑜𝑙𝑑) 𝜕𝑥 BMの更新式 勾配 𝜀: 小さい正の数(学習率) 𝑥 𝑓 初期値 勾配0で学習終了 更新 𝑏𝑖 𝑛𝑒𝑤 ← 𝑏𝑖 𝑜𝑙𝑑 +𝜀(𝐸 𝐷 𝑣𝑖 − 𝐸 𝐷 𝑣𝑖|𝜽 𝑜𝑙𝑑 ) 𝑤𝑖𝑗 𝑛𝑒𝑤 ← 𝑤𝑖𝑗 𝑜𝑙𝑑 +𝜀(𝐸 𝐷 𝑣𝑖 𝑣𝑗 − 𝐸 𝐷 𝑣𝑖 𝑣𝑗|𝜽 𝑜𝑙𝑑 )
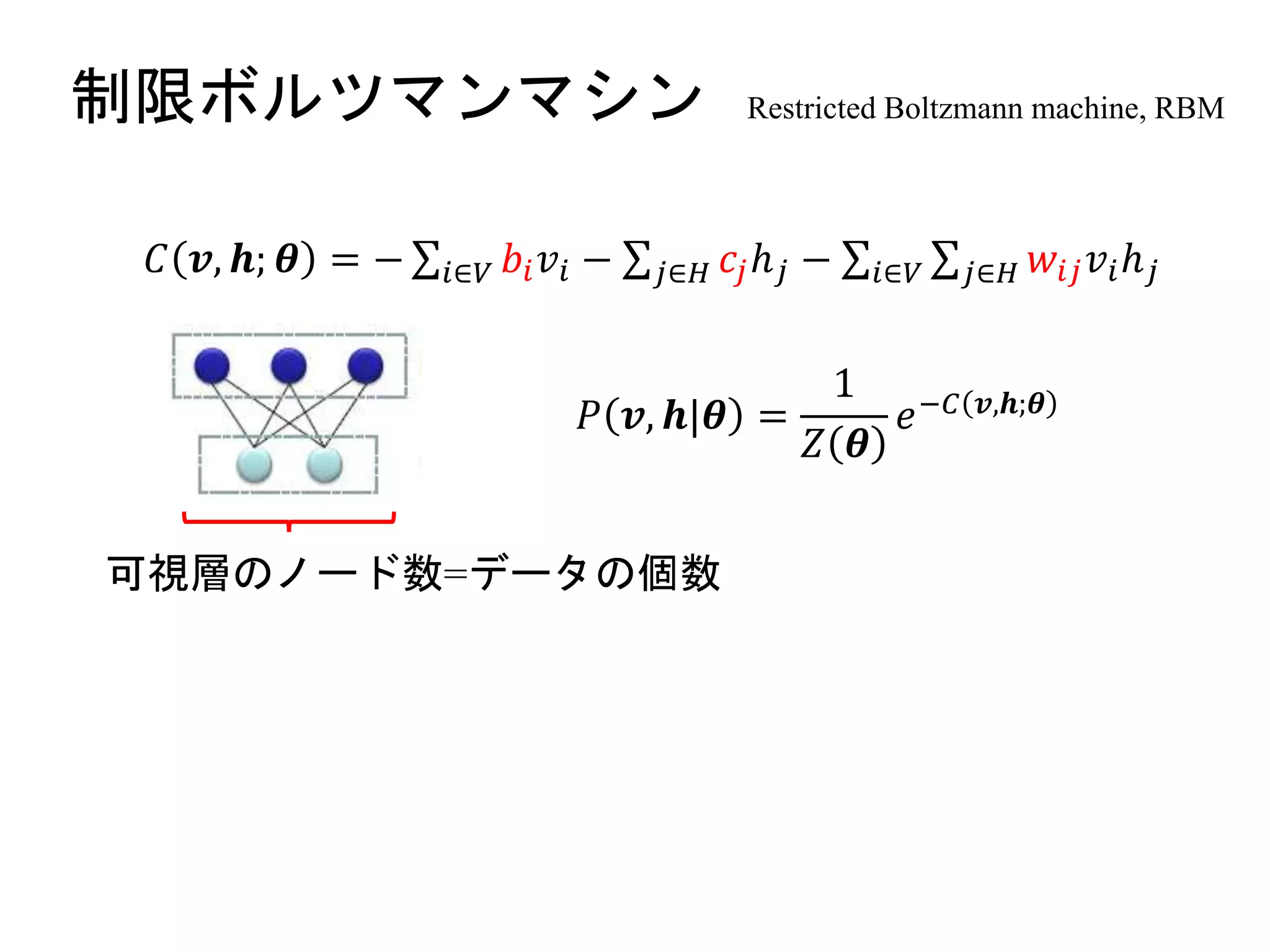
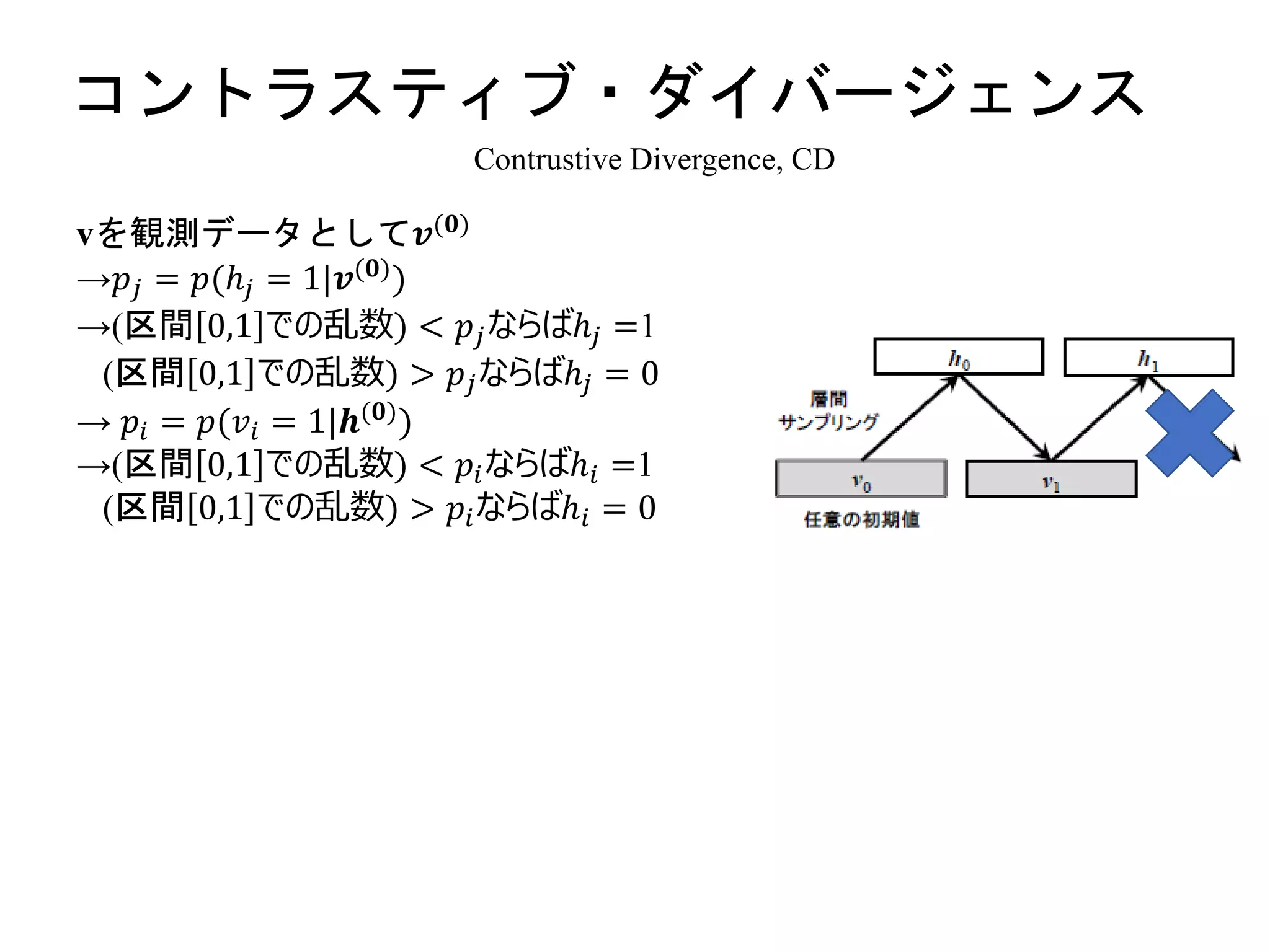
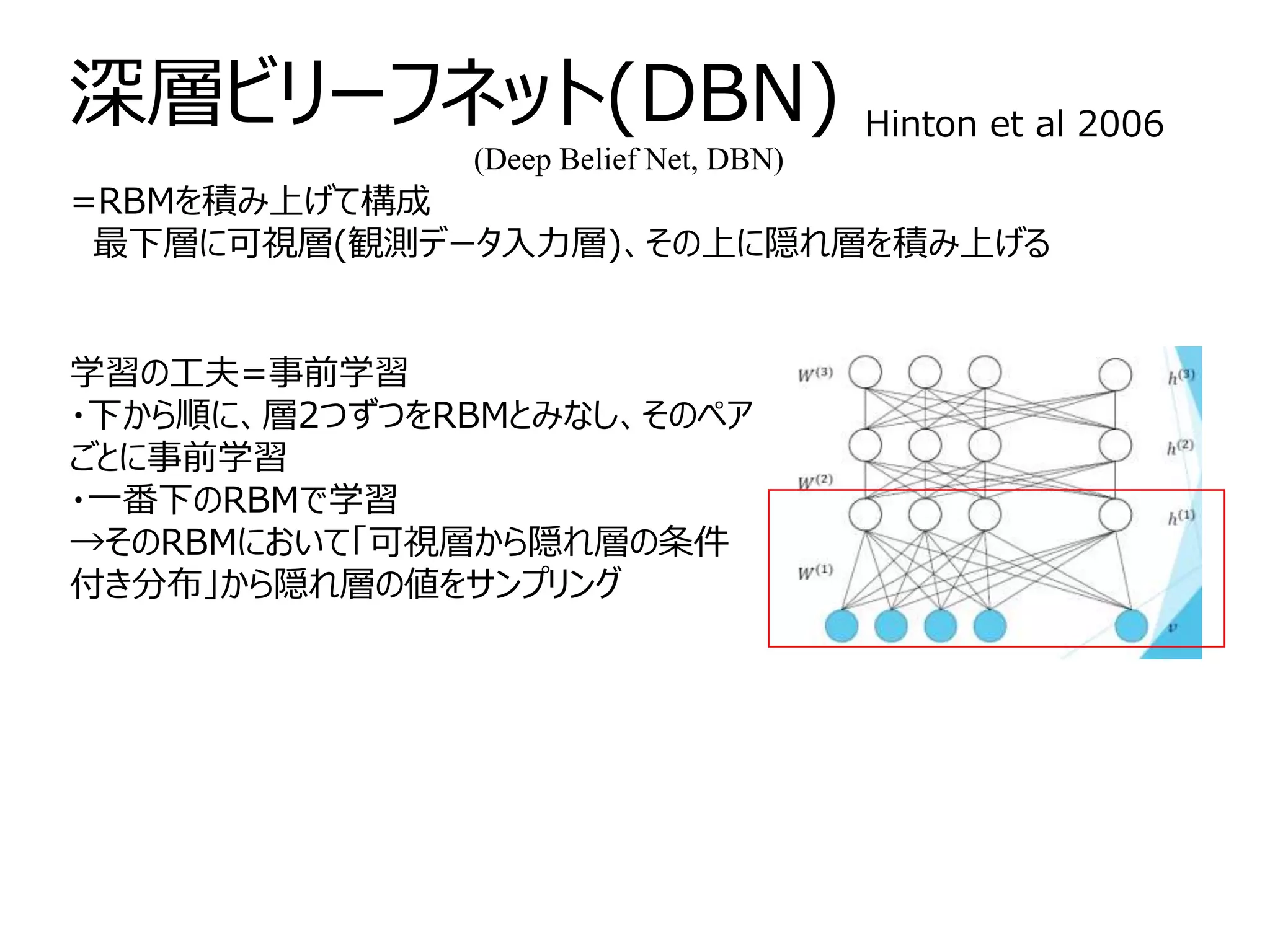
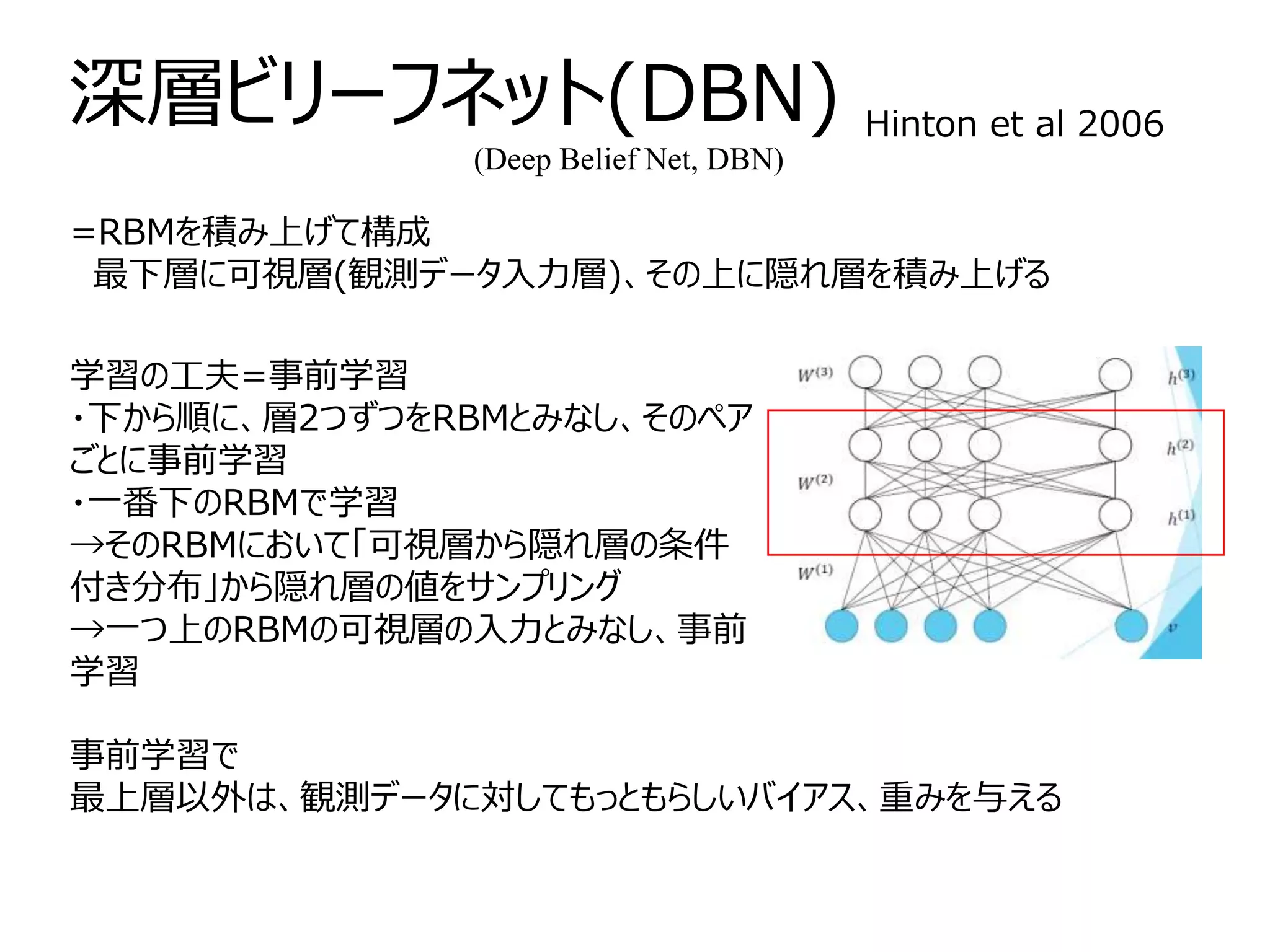
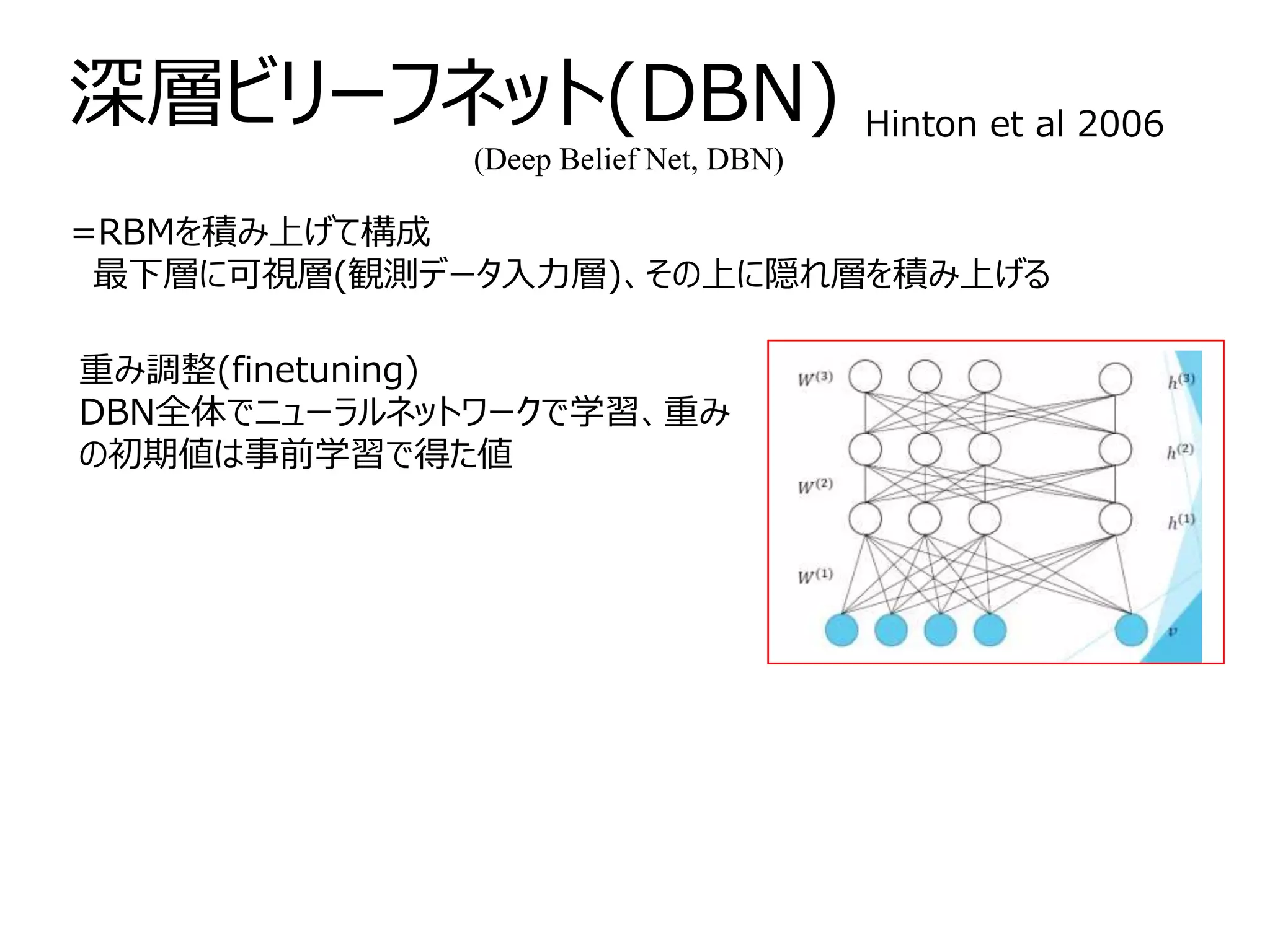
- 16. 制限ボルツマンマシン Restricted Boltzmannmachine, RBM ボルツマンマシンに ・「隠れ変数」を導入 →最尤推定時の目的関数に隠れ変数に関して周辺化した可視関数 のみの分布 ・制約を加える。 =可視ノード同士、隠れノード同士のリンク無し(層内結合無し) →・可視ノードのみからなる可視層、隠れノードのみからなる隠 れ層の2つの層 ・可視層内、隠れ層内の変数が互いに影響しない(条件付き独立) 深層学習の基本単位
- 17. 制限ボルツマンマシン Restricted Boltzmannmachine, RBM 𝐶 𝒗, 𝒉; 𝜽 = − 𝑖∈𝑉 𝑏𝑖 𝑣𝑖 − 𝑗∈𝐻 𝑐𝑗ℎ 𝑗 − 𝑖∈𝑉 𝑗∈𝐻 𝑤𝑖𝑗 𝑣𝑖ℎ 𝑗 𝑃 𝒗, 𝒉|𝜽 = 1 𝑍 𝜽 𝑒−𝐶 𝒗,𝒉;𝜽 可視層のノード数=データの個数
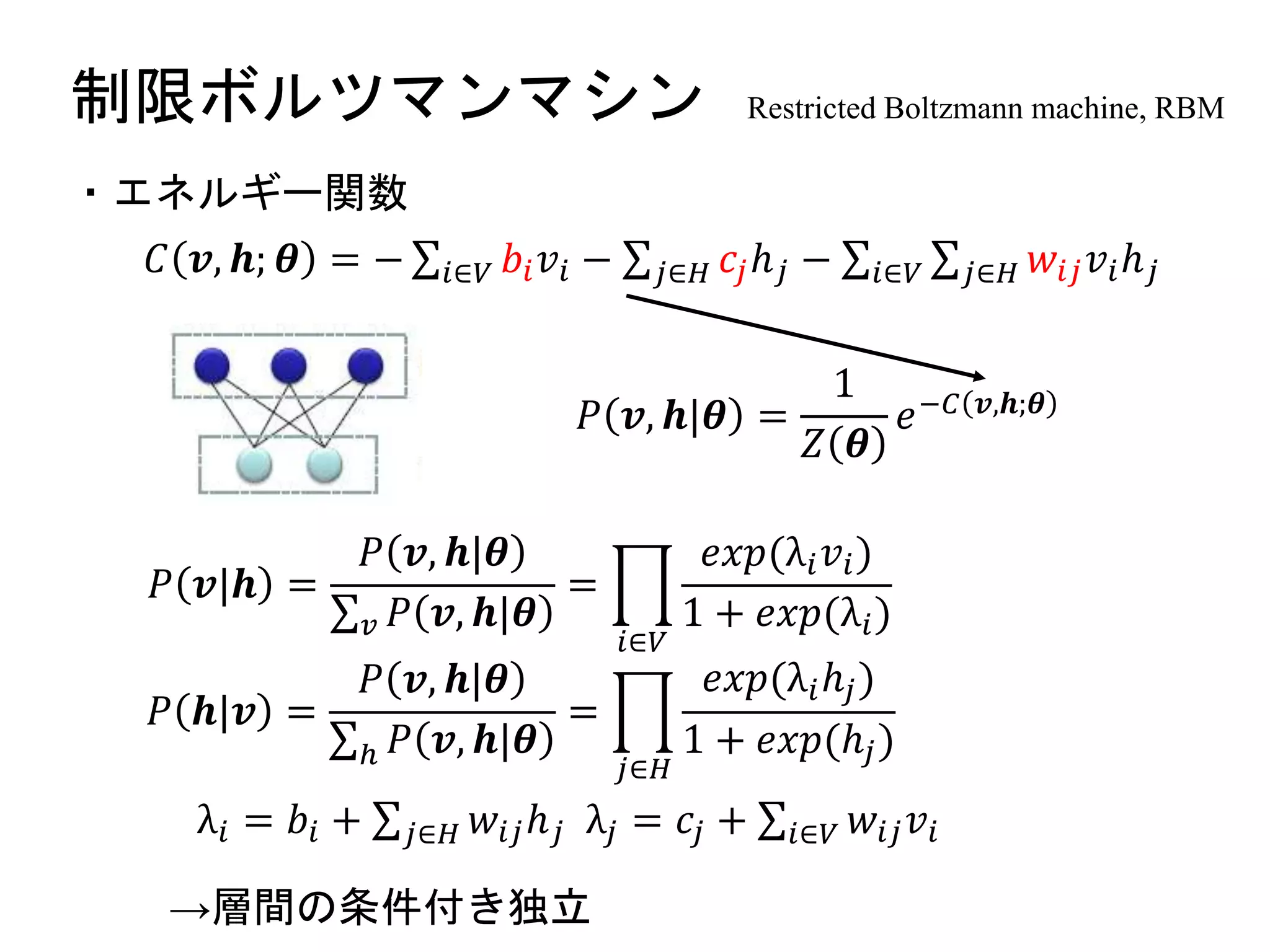
- 18. 制限ボルツマンマシン Restricted Boltzmannmachine, RBM 𝐶 𝒗, 𝒉; 𝜽 = − 𝑖∈𝑉 𝑏𝑖 𝑣𝑖 − 𝑗∈𝐻 𝑐𝑗ℎ 𝑗 − 𝑖∈𝑉 𝑗∈𝐻 𝑤𝑖𝑗 𝑣𝑖ℎ 𝑗 𝑃 𝒗, 𝒉|𝜽 = 1 𝑍 𝜽 𝑒−𝐶 𝒗,𝒉;𝜽 ・エネルギー関数 →層間の条件付き独立 𝑃 𝒗|𝒉 = 𝑃 𝒗, 𝒉|𝜽 𝑣 𝑃 𝒗, 𝒉|𝜽 = 𝑖∈𝑉 𝑒𝑥𝑝(λ𝑖 𝑣𝑖) 1 + 𝑒𝑥𝑝(λ𝑖) 𝑃 𝒉|𝒗 = 𝑃 𝒗, 𝒉|𝜽 ℎ 𝑃 𝒗, 𝒉|𝜽 = 𝑗∈𝐻 𝑒𝑥𝑝(λ𝑖ℎ𝑗) 1 + 𝑒𝑥𝑝(ℎ𝑗) λ𝑖 = 𝑏𝑖 + 𝑗∈𝐻 𝑤𝑖𝑗ℎ 𝑗 λ𝑗 = 𝑐𝑗 + 𝑖∈𝑉 𝑤𝑖𝑗 𝑣𝑖
- 19. RBMの学習 BMの時と同様に、対数尤度関数の勾配は、 1 𝑁 𝜕log𝐿 𝜕𝑏𝑖 = 1 𝑁 𝑛=1 𝑁 𝑣 𝑛𝑖 − 𝒗,𝒉 𝑣𝑖𝑝 𝒗, 𝒉|𝜽 1 𝑁 𝜕log𝐿 𝜕𝑐𝑖 = 1 𝑁 𝑛=1 𝑁 𝑝 ℎ𝑗 = 1|𝒗 𝑛 − 𝒗,𝒉 ℎ𝑗 𝑝 𝒗, 𝒉|𝜽 1 𝑁 𝜕log𝐿 𝜕𝑤𝑖𝑗 = 1 𝑁 𝑛=1 𝑁 𝑣 𝑛𝑖 𝑝 ℎ𝑗 = 1|𝒗 𝑛 − 𝒗,𝒉 ℎ𝑗 𝑝 𝒗, 𝒉|𝜽 →勾配の計算には可視層・隠れ層の期待値が必要(第2項) →組み合わせ爆発により直接の計算は困難 →コントラスティブ・ダイバージェンスで期待値を近似的に計 算
- 20. コントラスティブ・ダイバージェンス vを観測データとして𝒗(𝟎) →𝑝𝑗 = 𝑝(ℎ𝑗= 1|𝒗(𝟎) ) →(区間 0,1 での乱数) < 𝑝𝑗ならばℎ𝑗 =1 (区間 0,1 での乱数) > 𝑝𝑗ならばℎ𝑗 = 0 → 𝑝𝑖 = 𝑝(𝑣𝑖 = 1|𝒉(𝟎)) →(区間 0,1 での乱数) < 𝑝𝑖ならばℎ𝑖 =1 (区間 0,1 での乱数) > 𝑝𝑖ならばℎ𝑖 = 0 Contrustive Divergence, CD
- 21.
- 22.
- 23.