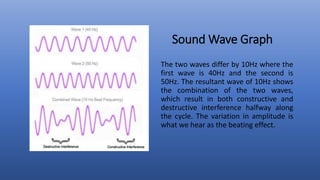
Two sound waves that are close in frequency will interfere with each other, creating a phenomenon known as beats. Beats occur when the amplitude of the resulting sound wave varies over time due to the constructive and destructive interference between the two waves. The beat frequency is equal to the difference between the two original frequencies. Musicians can use beats to tune instruments by adjusting frequencies until the beating stops.

1. Interference: Beats
Learning Object 7
Ian Yen / Physics 101

2. Information for Starters
• Constructive and destructive interference of waves can be separated
by intervals of time rather than intervals of position.
• Beat is defined as a type of variation in amplitude as a result of two
waves having slightly different frequencies.
• When the frequency difference is large, human ears can detect the
sounds as two distinct tones rather than one.

3. Sound Wave Graph
The two waves differ by 10Hz where the
first wave is 40Hz and the second is
50Hz. The resultant wave of 10Hz shows
the combination of the two waves,
which result in both constructive and
destructive interference halfway along
the cycle. The variation in amplitude is
what we hear as the beating effect.

4. Mathematics of Beats (1D)
Consider two waves with equal amplitude, different frequencies (w1
and w2), different wavelengths, and different wave numbers.
s₁(x,t) = Acos(k₁x - w₁t) and s₂(x,t) = Acos(k₂x - w₂t)
To find the resulting wave, we simply add the two waves together:
S(x,t) = s₁(x,t) + s₂(x,t) = Acos(k₁x - w₁t) + Acos(k₂x - w₂t)
After several mathematical procedures, we end up with:
= 2Acos[(k₁+k₂/2)x – (w₁+w₂/2)t] x cos[(k₁-k₂/2)x – (w₁-w₂/2)t]
Mean Angular Frequency: w = (w₁+w₂)/2
Angular Frequency Difference: Δw = (w₁-w₂)/2
Final Equation: 2Acos(wt)cos(Δwt)

5. Beat Frequencies
When the two waves are close to each other in terms of frequency,
there is a tone that has the mean frequency and the amplitude varies by
the difference in angular frequency.
Beat frequency can indicate whether an instrument is out of tune or
not. By adjusting the frequency of the notes, musicians do this until the
beating stops.

6. Check Your Understanding
Someone in your choir can’t keep a tune. You know that you are singing
at a frequency of 512Hz but you hear Mr. Bates singing out of key. You
remember back to Physics 101 and note that the beat frequency is 3Hz.
a) What are the possible notes that Mr. Bates is singing?
b) The equation of motion of a sound wave is given by y=Acos(kx-wt)
and another is given by y=Acos(kx-(w+E)t). Assume you are standing at
the origin (x=0) and assume that E is much less than w.
i) Write and simplify the equation that describes the superimposition
of the two waves

7. Answers
a) Possible notes include 509Hz and 515Hz.
b) y₁ = Acos(kx-(w+E)t) and y₂ = Acos(kx-wt). In order to write the
superimposition of the two waves, we have to simplify the two
equations first to get rid of kx since beats only depend on time.
y₁ = Acos((w+E)t) and y₂ = Acos(wt). In order to obtain the equation, we
must combine these two waves.
y₁ + y₂ = Acos((w+E)t) + Acos(wt)
y₁ + y₂ = A[cos((2w+E)/2)tcos(-Et/2)]
y₁ + y₂ = Acos(wt)cos(Et/2)