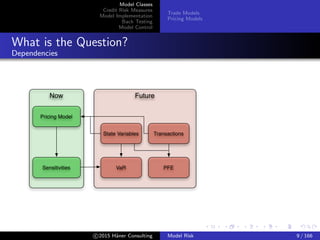
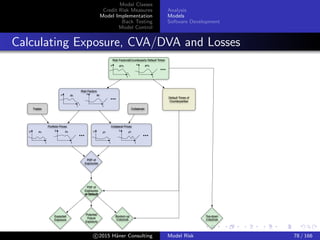
This document discusses model classes, credit risk measures, model implementation, back testing, and model control. It covers various types of models including trade models, pricing models, and risk models. It also discusses different ways of measuring credit risk including measures of severity such as exposure at default and loss given default, as well as measures of frequency like probability of default. Finally, it discusses pricing models that incorporate credit risk.

























![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Types of Measures
Severity
Frequency
Pricing Credit Risk
Statistical Measures
Single Netting Set
Definition (Potential Future Exposure)
PFE(t) = max 0, p(t)|τ = t
τ : time at which CP defaults
Definition (Expected Exposure (EE))
EE(t) = E[PFE]
Definition (Expected Positive Exposure)
EPE(T) =
1
T
T
0
EE(t) dt
c 2015 H¨aner Consulting Model Risk 27 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-27-320.jpg)























![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Gaussian Approximation
Need to estimate E[p(T)], E[p2(Ti )] at some future times T:
Performing Taylor expansion for price p around expected risk
factor:
p(x(T), T) ≈ p(x0(T), T) +
i
∂p(x0(T), T)
∂xi
∆xi (T)
+
1
2
ij
∂2p(x0(T), T)
∂xi ∂xj
∆xi (T)∆xj (T)
x0(T) ≡ E[x(T)]
∆xi (T) ≡ xi (T) − x0,i (T)
c 2015 H¨aner Consulting Model Risk 51 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-51-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Gaussian Approximation
The expectation value M of the price is hence
M(T) ≈ p(x0(T), T) +
1
2
ij
γij (T)Ωij (T)
M(T) ≡ E[p(x(T), T)]
γij (T) ≡
∂2p(x0(T), T)
∂xi ∂xj
Ωij (T) ≡ E[∆xi (T)∆xj (T)]
For the variance V we obtain up to second order in ∆x:
V (T) ≈
ij
δi (T)δj (T)Ωij (T)
V (T) ≡ E[(p(x(T), T) − E[p(x(T), T)])2
]
δi (T) ≡
∂p(x0(T), T)
∂xic 2015 H¨aner Consulting Model Risk 52 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-52-320.jpg)
































![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Gaussian Dependency Modelling
Goal
Express random vector ξ with correlated ξi as
linear combination of
uncorrelated
random factors ηi :
ξ = Mη
E[ξi ξj ] − E[ξi ]E[ξj ] ≡ Ωij
E[ηi ηj ] − E[ηi ]E[ηj ] = λ2
i δij diagonal, pos. sem. def.
What to consider?
Ω?
correlation matrix?
c 2015 H¨aner Consulting Model Risk 86 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-86-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Principal Component Analysis
Dimensional Analysis
Risk factors ξi not dimension-less!
interest rate :[T−1]
stock price :[Cash]
volatility: [T−1
2 ]
→ Ωij may have different dimensions,i.e. Ω in general not a
physically meaningful quantity!
c 2015 H¨aner Consulting Model Risk 87 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-87-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Principal Component Analysis
Solution
Consider instead of Ω following matrix Φ:
Φij ≡
∂f (ξ)
∂ξi
∂f (ξ)
∂ξj
Ωij
f : some function
For dimensionality [Φ]:
[Φij ] =
[f ]
[ξi ]
[f ]
[ξj ]
[ξi ][ξj ] = [f 2
] ∀i, j (3)
c 2015 H¨aner Consulting Model Risk 88 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-88-320.jpg)




![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Maximum Likelihood Estimation
Systematic way to calibrate
Approach
Parametric model with parameters α ↔ parametric measure µα:
µα(Γ) = e−Sα(Γ)
D[Γ]
Assume: historical path ΓH is the most likely one. Find α∗ such
that:
µα∗ (ΓH) = max
α
µα(ΓH)
c 2015 H¨aner Consulting Model Risk 93 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-93-320.jpg)




![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Parities
Example (Relative Purchasing Power Parity)
pf (t1)(1 + if )X(t2) = pd (t2)(1 + id )
pd/f : domestic/foreign price
id/f : domestic/foreign 1 yr inflation rate
X : Exchange rate
Yields after averaging
E[X(t2)]
X(t1)
=
1 + Id
1 + If
where I is the expected inflation rate.
c 2015 H¨aner Consulting Model Risk 98 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-98-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Parities
Example (International Fisher Effect (Uncovered Parity))
(1 + rd/f ) = (1 + ρd/f )(1 + id/f )
rd/f : domestic/foreign nominal 1 yr interest rate
ρd/f : real rdomestic/foreign 1 yr interest rate
Assumingρd = ρf gives
E[X(t2)]
X(t1)
=
1 + rd
1 + rf
c 2015 H¨aner Consulting Model Risk 99 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-99-320.jpg)










![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Analysis
Models
Software Development
Garch Model
The dynamics of the returns is then assumed to follow a
Garch(1,1) process
Xn = µ + n t ∼ iid(0, σ2
n) (6)
σ2
n+1 = α + βσ2
n + γ 2
n (7)
The asymptotic value σ2
∞ = limn→∞ E[σ2
n] is then obtained by
equation (7) noting, that E[ 2] = σ2 and E[σ2
n+1] → E[σ2
n]:
σ∞ =
α
1 − β − γ
(8)
c 2015 H¨aner Consulting Model Risk 110 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-110-320.jpg)





































![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Regulatory Requirements
Measuring Model Performance
Radon-Nikodym Derivative
Distance of model Q and end empirical measure P in terms of dP
dQ:
EP[f ] = EQ[
dP
dQ
f ] (9)
Compare P and Q
Direct dP
dQ ≈ id?
Expectation values Empirical expectation measures in terms of
model expectations
Relative Entropy Kullback-Leibler entropy → information
geometry (see [?])
c 2015 H¨aner Consulting Model Risk 151 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-151-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Regulatory Requirements
Measuring Model Performance
Radon-Nikodym Derivative
Let ξ be a scalar stochastic variable (e.g. portfolio price π(t))
Definition
P empirical, Q model CDF
Ψ : [0, 1] → [0, 1] (10)
Ψ(α) = P(Q−1
(α)) (11)
Radon-Nikodym derivative ψ
EP[f ] = EQ[ψ(α)f ] (12)
ψ(α) =
dΨ(α)
dα
(13)
c 2015 H¨aner Consulting Model Risk 152 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-152-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Regulatory Requirements
Measuring Model Performance
Example
(a)
0.0 0.2 0.4 0.6 0.8 1.0
α
0.0
0.2
0.4
0.6
0.8
1.0
Ψ(α)
[x]=100.00;σ=0.40
[x]=110.00;σ=0.40
[x]=90.00;σ=0.40
[x]=100.00;σ=0.44
[x]=100.00;σ=0.36
0.8
1.0
1.2
1.4
1.6
1.8
ψ(α)
[x]=100.00;σ=0.40
[x]=110.00;σ=0.40
[x]=90.00;σ=0.40
[x]=100.00;σ=0.44
[x]=100.00;σ=0.36
c 2015 H¨aner Consulting Model Risk 153 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-153-320.jpg)
![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Regulatory Requirements
Measuring Model Performance
Cumulative Distribution Functions
Cumulative distribution function (CDF) for some state variable ξ
expressed as expectation:
Definition
P(ξ0) = EP[Θ(ξ − ξ0)] (14)
where Θ is the Heaviside function.
c 2015 H¨aner Consulting Model Risk 154 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-154-320.jpg)





![Model Classes
Credit Risk Measures
Model Implementation
Back Testing
Model Control
Regulatory Requirements
Measuring Model Performance
Problems using metrics for Ψ
20 40 60 80 100 120 140 160
strike K
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
EE
EE
[x]=100.00;σ=0.40
[x]=110.00;σ=0.40
[x]=90.00;σ=0.40
[x]=100.00;σ=0.44
[x]=100.00;σ=0.36
Figure : Comparing EEs for a forward using log-normal distributions with
different parameters
c 2015 H¨aner Consulting Model Risk 160 / 166](https://image.slidesharecdn.com/modelrisk-131222082242-phpapp01/85/Model-Risk-for-Pricing-and-Risk-Models-in-Finance-160-320.jpg)





