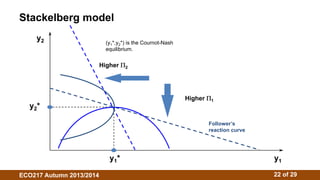
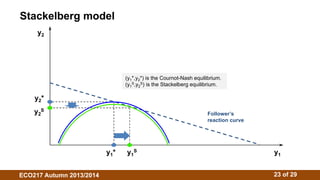
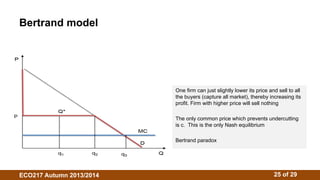
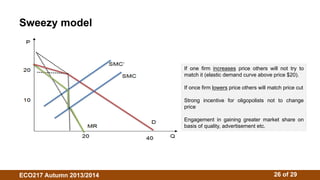
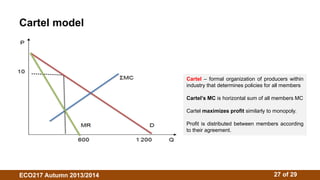
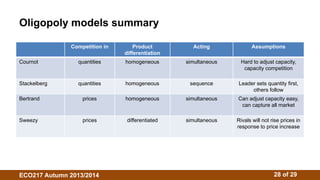
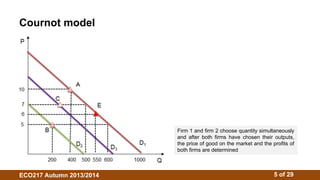
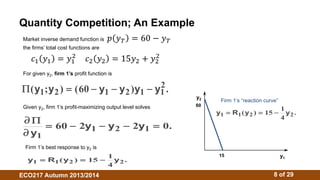
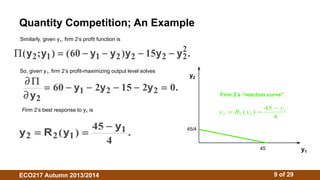
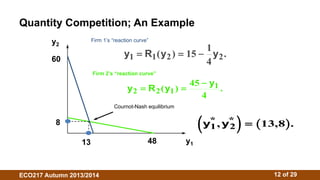
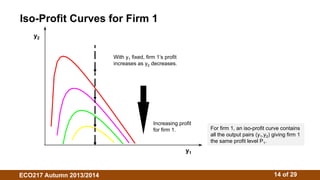
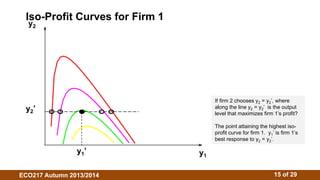
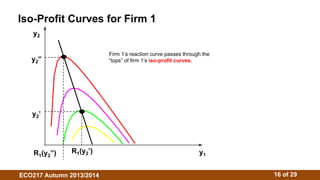
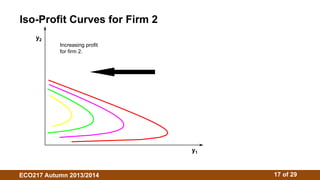
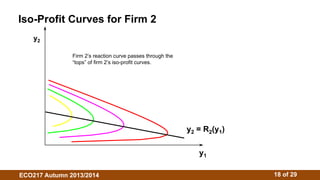
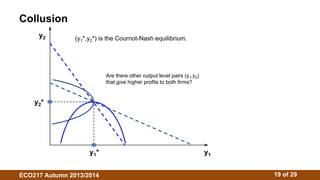
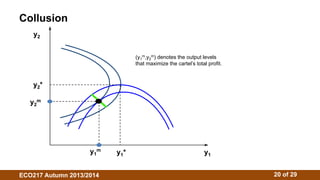
1. Oligopoly is a market structure with few sellers who recognize their interdependence. Each seller's actions impact competitors and reactions are uncertain. 2. There is no single oligopoly theory due to different behavioral assumptions. Models include Cournot (firms choose quantities), Stackelberg (firms choose quantities sequentially), and Bertrand (firms choose prices). 3. The Cournot model assumes firms choose outputs simultaneously. Their reaction functions determine the Cournot-Nash equilibrium where outputs maximize profits given competitors' outputs. Isoprofit curves illustrate profit-maximizing outputs under different competitor outputs.

1. 11 | Oligopoly
Cournot model, Stackelberg model, Isoprofit curves
ECO217 Microeconomics I

2. Oligopoly
Oligopoly – market organization in which are few sellers of a commodity
Seller side is few big participants – oligopolists
Demand side – many participants – none of them can influence price
Oligopolists can compete with
homogenous good – like steel, aluminum, cement or with
heterogeneous good – automobiles, tires, television sets etc.
Supply side participants has full information about number of competitors and their sales.
Information about other competitors price can be full or partial
Oligopoly usually generate high profit and has strategies to deter other from coming into market
ECO217 Autumn 2013/2014 2 of 29

3. Oligopoly
Actions of each seller will affect other sellers
Reactions of other firms are unknown
Since cannot construct one definite demand curve, oligopoly have indeterminate solutions
Each behavioral assumption will have different solution
No general theory of oligopoly exist
Duopoly – market organization where are two firms selling product
ECO217 Autumn 2013/2014 3 of 29

4. In Cournot model each firm
assumes that other firm will
keep output constant Cournot model
ECO217 Autumn 2013/2014 4 of 29

5. Cournot model
Firm 1 and firm 2 choose quantity simultaneously
and after both firms have chosen their outputs,
the price of good on the market and the profits of
both firms are determined
ECO217 Autumn 2013/2014 5 of 29

6. Reaction function
Reaction function – function
that specifies a firms optimal
choice for some variable such as
output, given choices of its
competitors
ECO217 Autumn 2013/2014 6 of 29

7. Reaction function; Quantity Competition
Assume that firms compete by choosing output levels.
If firm 1 produces y1 units and firm 2 produces y2 units, total quantity supplied is y1 + y2.
The market price will be p(y1+ y2) that is depends from both outputs - y1 and y2
Suppose firm 1 takes firm 2’s output level choice y2 as given. Then firm 1 sees its profit function as
1(y1;y2)  p(y1  y2)y1  c1(y1).
Given y2, what output level y1 maximizes firm 1’s profit?
ECO217 Autumn 2013/2014 7 of 29

8. Quantity Competition; An Example
Market inverse demand function is ݌ ݕ் = 60 − ݕ்
the firms’ total cost functions are
ܿଵ ݕଵ = ݕଵ
ଶ ܿଶ ݕଶ = 15ݕଶ + ݕଶ
For given y2, firm 1’s profit function is
ଶ
( y 1 ; y 2 )  ( 60  y 1  y 2 ) y 1 
y 2
. 1 Given y2, firm 1’s profit-maximizing output level solves



y
y y y
1
 60  2 1  2  2 1  0.
Firm 1’s best response to y2 is
y1 R1 y2 15 1y2
 ( )   .
4
y2
Firm 1’s “reaction curve”
y1 R1 y2 15 1y2
 ( )   .
4
y1
60
15
ECO217 Autumn 2013/2014 8 of 29

9. Quantity Competition; An Example
Similarly, given y1, firm 2’s profit function is
( y 2
2 ; y 1 )  ( 60  y 1  y 2 ) y 2  15 y 2 
y . 2 So, given y1, firm 2’s profit-maximizing output level solves



y
y y y
2
 60  1  2 2  15  2 2  0.
Firm 2’s best response to y1 is
y R y y
2 2 1
45 1
 ( )   .
4
y2
( ) 45 1
y  R y   y
ECO217 Autumn 2013/2014 9 of 29
y1
Firm 2’s “reaction curve”
4
2 2 1
45/4
45

10. Quantity Competition; An Example
An equilibrium is when each firm’s output level is a best response to the other firm’s output level, for then neither
wants to deviate from its output level.
A pair of output levels (y1*,y2*) is a Cournot-Nash equilibrium if
y1* = R1(y2*) and y2* = R2(y1*)
ECO217 Autumn 2013/2014 10 of 29

11. Quantity Competition; An Example
y1 R1 y2 15 1y2
*
*  ( * )   * y R y y
4
and *  ( *
)   .
2 2 1
45 1
4
*
    
*
y1 y y
15 1 1
* 1
13
4
45
4
 
 
 
*    8.
y2
45 13
4
The Cournot-Nash equilibrium is
(y*1,y*2 )  (13,8).
ECO217 Autumn 2013/2014 11 of 29

12. Quantity Competition; An Example
y2
y1 R1 y2 15 1y2
 ( )   .
y R y y
2 2 1
45 1
 ( )   .
y1
Firm 1’s “reaction curve”
Firm 2’s “reaction curve”
Cournot-Nash equilibrium
48
60
4
8
13
4
y*1,y*2  13,8.
ECO217 Autumn 2013/2014 12 of 29

13. Iso-Profit Curves
ECO217 Autumn 2013/2014 13 of 29

14. Iso-Profit Curves for Firm 1
y2
Increasing profit
for firm 1. For firm 1, an iso-profit curve contains
y1
With y1 fixed, firm 1’s profit
increases as y2 decreases.
all the output pairs (y1,y2) giving firm 1
the same profit level P1.
ECO217 Autumn 2013/2014 14 of 29

15. Iso-Profit Curves for Firm 1
y2
y1
If firm 2 chooses y2 = y2’, where
along the line y2 = y2’ is the output
level that maximizes firm 1’s profit?
The point attaining the highest iso-profit
curve for firm 1. y1’ is firm 1’s
best response to y2 = y2’.
y2’
y1’
ECO217 Autumn 2013/2014 15 of 29

16. Iso-Profit Curves for Firm 1
y2
Firm 1’s reaction curve passes through the
“tops” of firm 1’s iso-profit curves.
y1
y2”
y2’
R1(y2”) R1(y2’)
ECO217 Autumn 2013/2014 16 of 29

17. Iso-Profit Curves for Firm 2
y2
y1
Increasing profit
for firm 2.
ECO217 Autumn 2013/2014 17 of 29

18. Iso-Profit Curves for Firm 2
y2
y2 = R2(y1)
y1
Firm 2’s reaction curve passes through the
“tops” of firm 2’s iso-profit curves.
ECO217 Autumn 2013/2014 18 of 29

19. Collusion
y2
(y1*,y2*) is the Cournot-Nash equilibrium.
Are there other output level pairs (y1,y2)
that give higher profits to both firms?
y1* y1
y2*
ECO217 Autumn 2013/2014 19 of 29

20. Collusion
y2
(y1
m,y2
m) denotes the output levels
that maximize the cartel’s total profit.
y1* y1
y2*
y2
m
y1
m
ECO217 Autumn 2013/2014 20 of 29

21. Stackelberg – sequential
competition in quantities
where on firm acts as a
quantity leader, choosing
quantity first, with other firm
acting as follower
Stackelberg model
ECO217 Autumn 2013/2014 21 of 29

22. Stackelberg model
y2
(y1*,y2*) is the Cournot-Nash
equilibrium.
Higher 2
Higher 1
Follower’s
reaction curve
y1* y1
y2*
ECO217 Autumn 2013/2014 22 of 29

23. Stackelberg model
y2
(y1*,y2*) is the Cournot-Nash equilibrium.
(y1
S,y2
S) is the Stackelberg equilibrium.
Follower’s
reaction curve
y1* y1
y2*
y1
S
y2
S
ECO217 Autumn 2013/2014 23 of 29

24. A model of oligopolistic
competition where firms
compete by setting prices Bertrand model
ECO217 Autumn 2013/2014 24 of 29

25. Bertrand model
One firm can just slightly lower its price and sell to all
the buyers (capture all market), thereby increasing its
profit. Firm with higher price will sell nothing
The only common price which prevents undercutting
is c. This is the only Nash equilibrium
Bertrand paradox
ECO217 Autumn 2013/2014 25 of 29

26. Sweezy model
If one firm increases price others will not try to
match it (elastic demand curve above price $20).
If once firm lowers price others will match price cut
Strong incentive for oligopolists not to change
price
Engagement in gaining greater market share on
basis of quality, advertisement etc.
ECO217 Autumn 2013/2014 26 of 29

27. Cartel model
Cartel – formal organization of producers within
industry that determines policies for all members
Cartel’s MC is horizontal sum of all members MC
Cartel maximizes profit similarly to monopoly.
Profit is distributed between members according
to their agreement.
ECO217 Autumn 2013/2014 27 of 29

28. Oligopoly models summary
Competition in Product
differentiation
Acting Assumptions
Cournot quantities homogeneous simultaneous Hard to adjust capacity,
capacity competition
Stackelberg quantities homogeneous sequence Leader sets quantity first,
others follow
Bertrand prices homogeneous simultaneous Can adjust capacity easy,
can capture all market
Sweezy prices differentiated simultaneous Rivals will not rise prices in
response to price increase
ECO217 Autumn 2013/2014 28 of 29

29. Dr. Martins Priede
ECO217 Microeconomics I
martins.priede@xjtlu.edu.cn
ECO217 Autumn 2013/2014 29 of 29