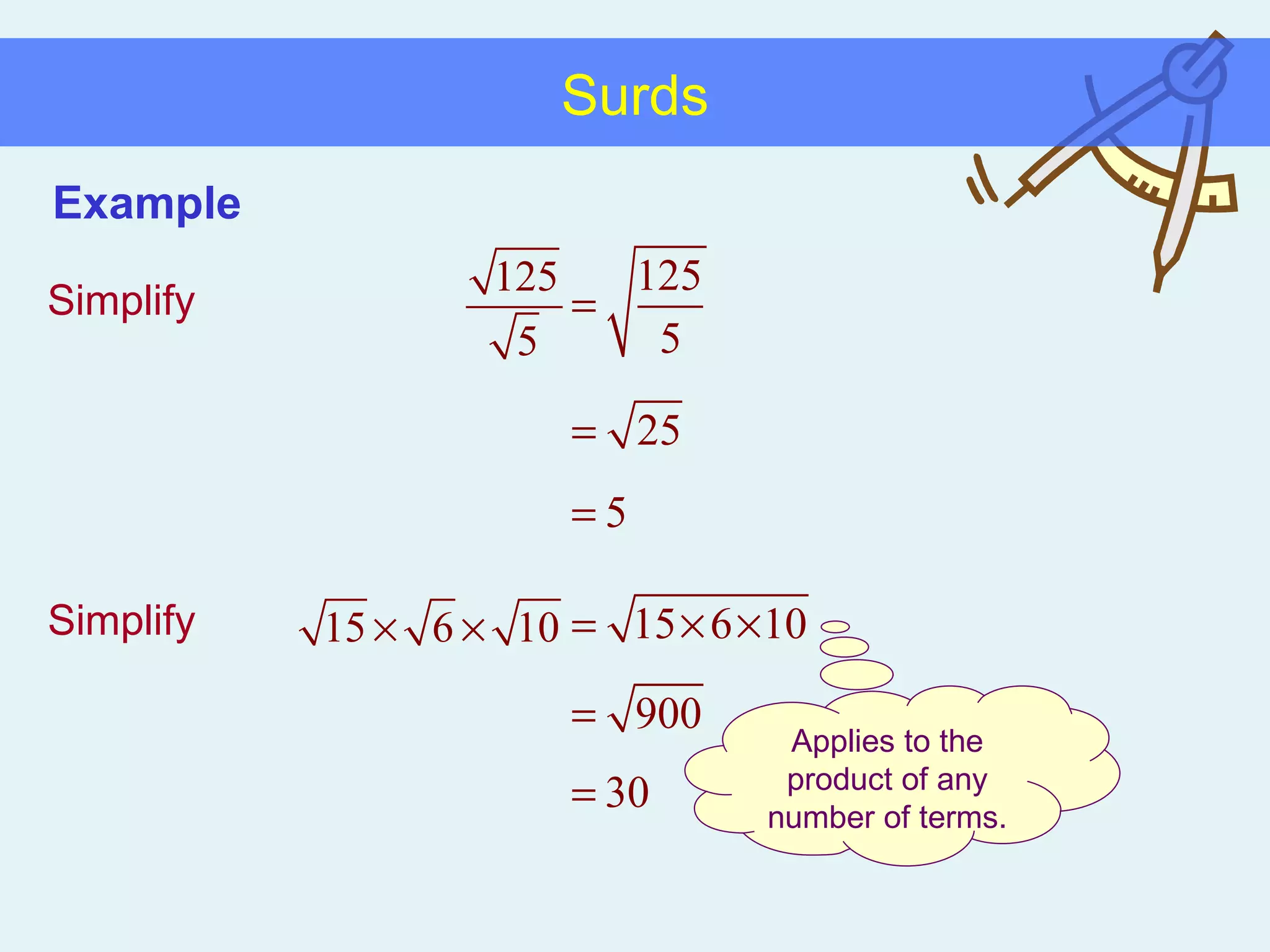
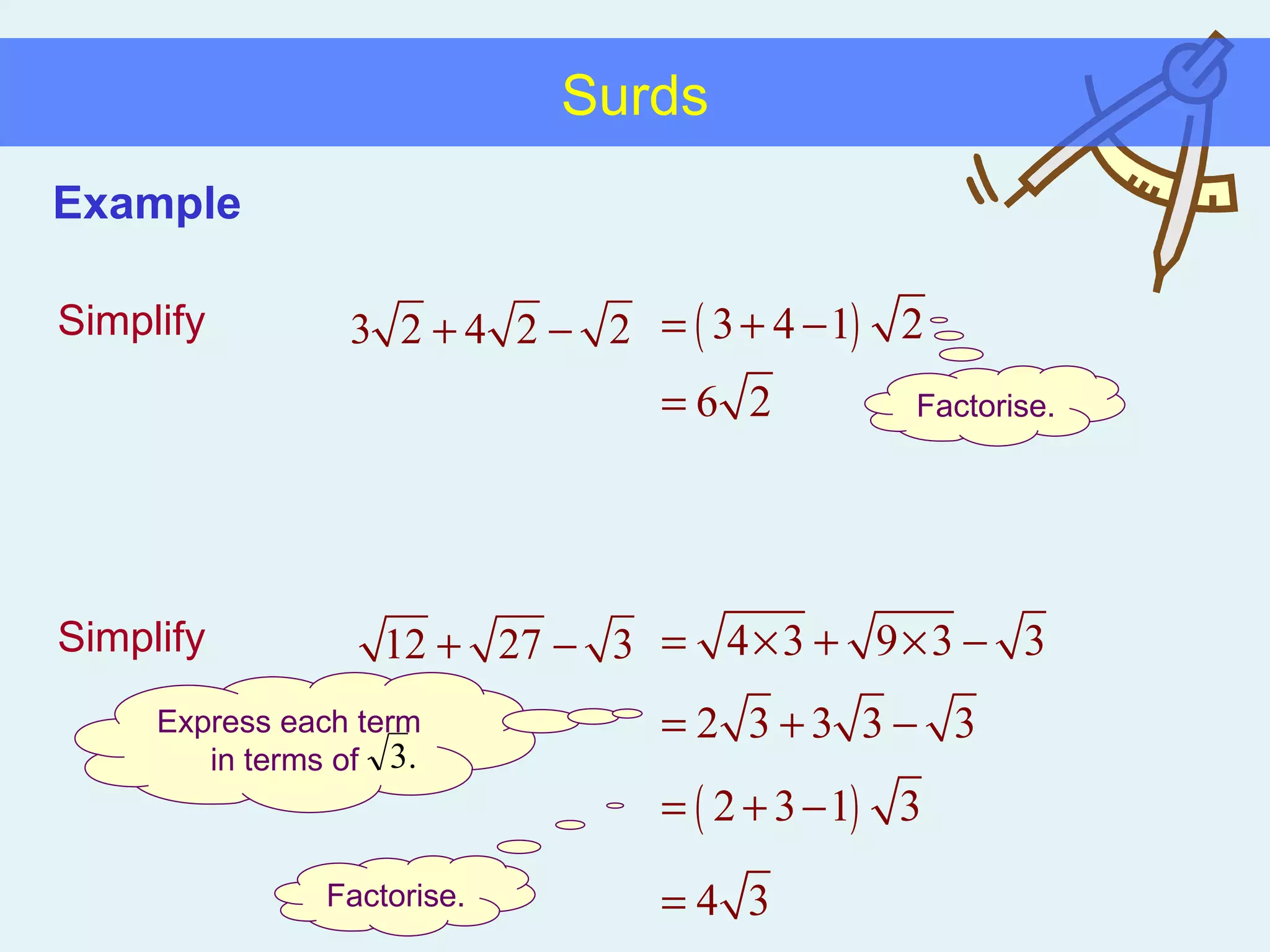
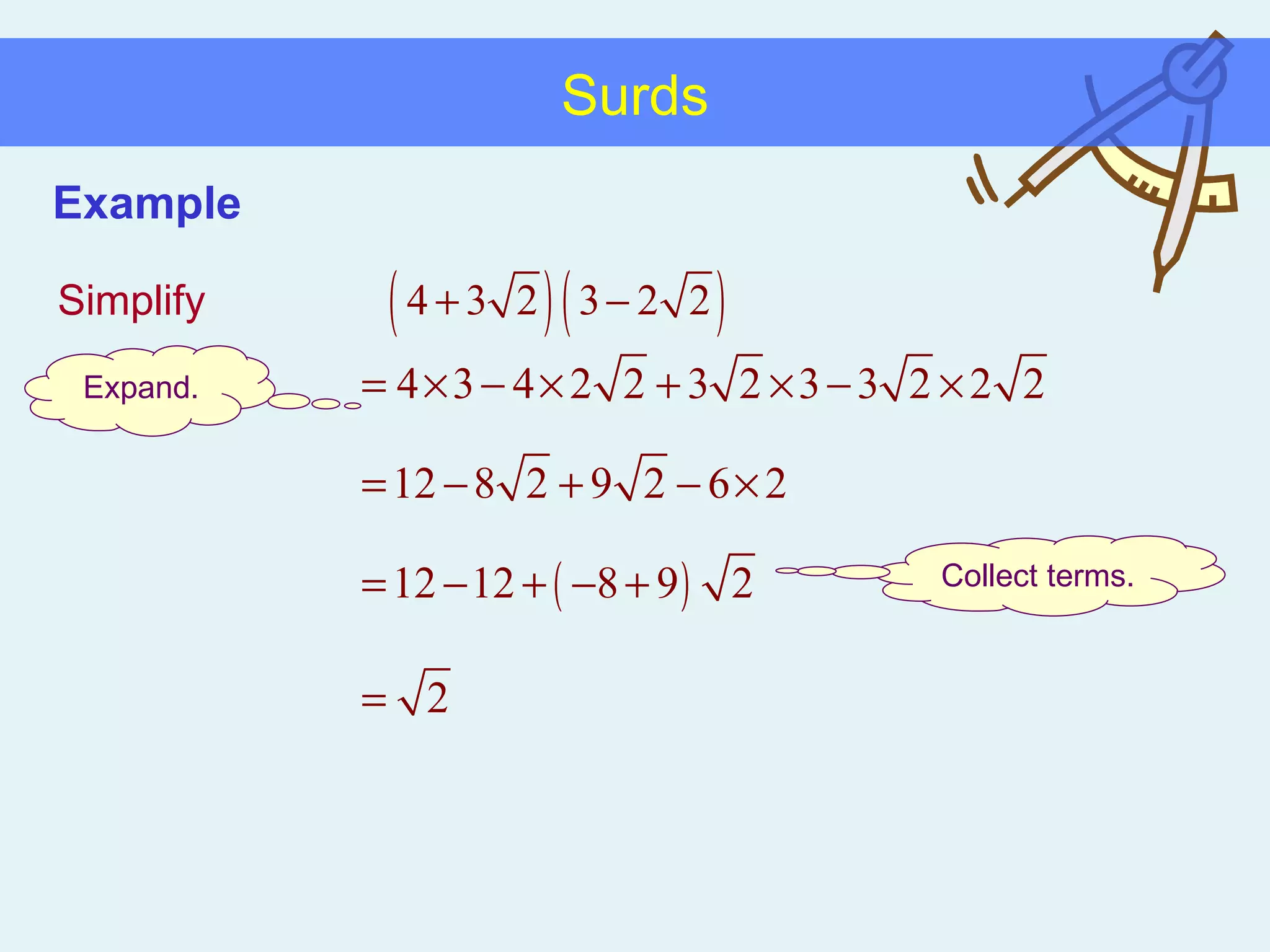
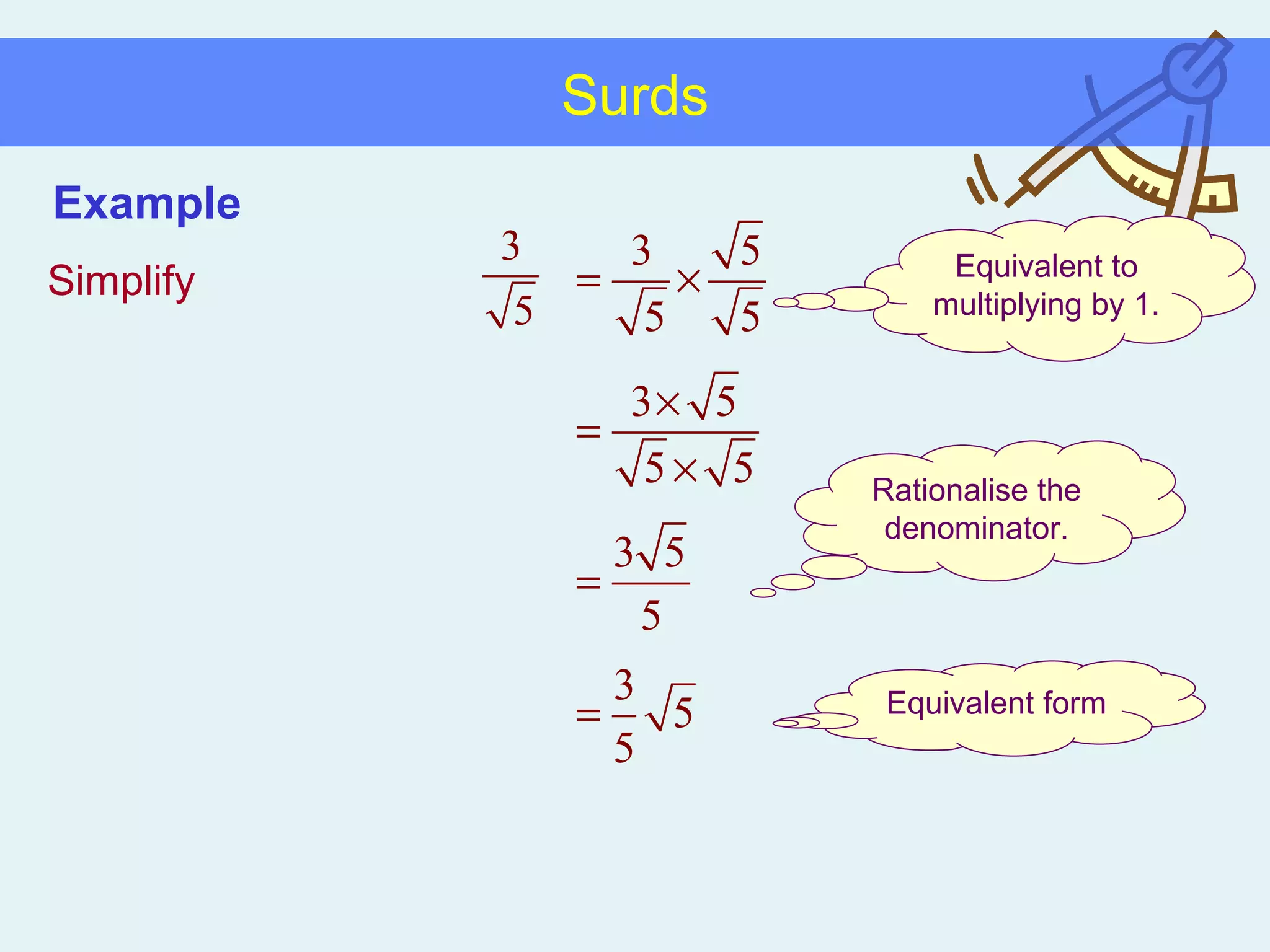
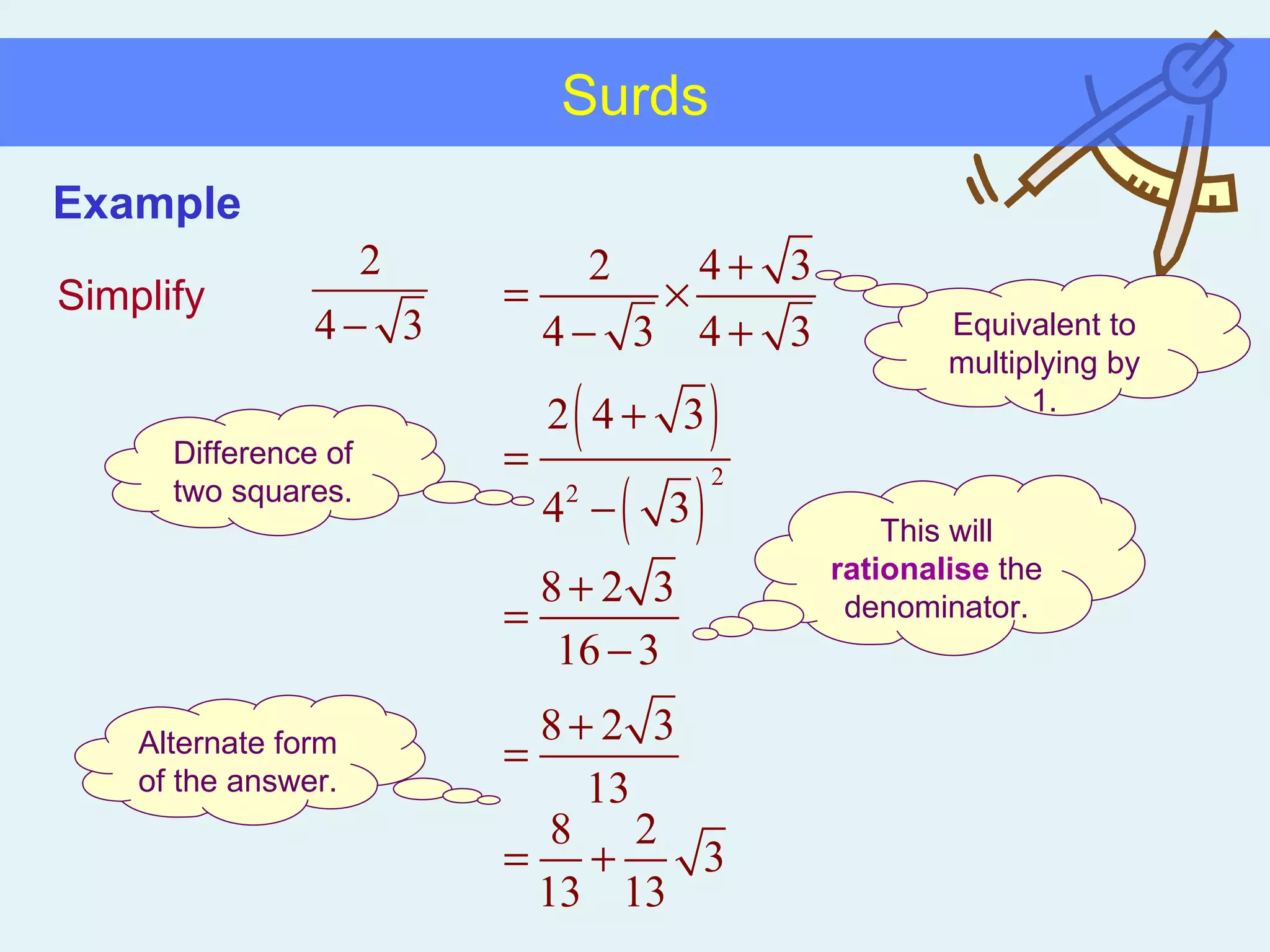
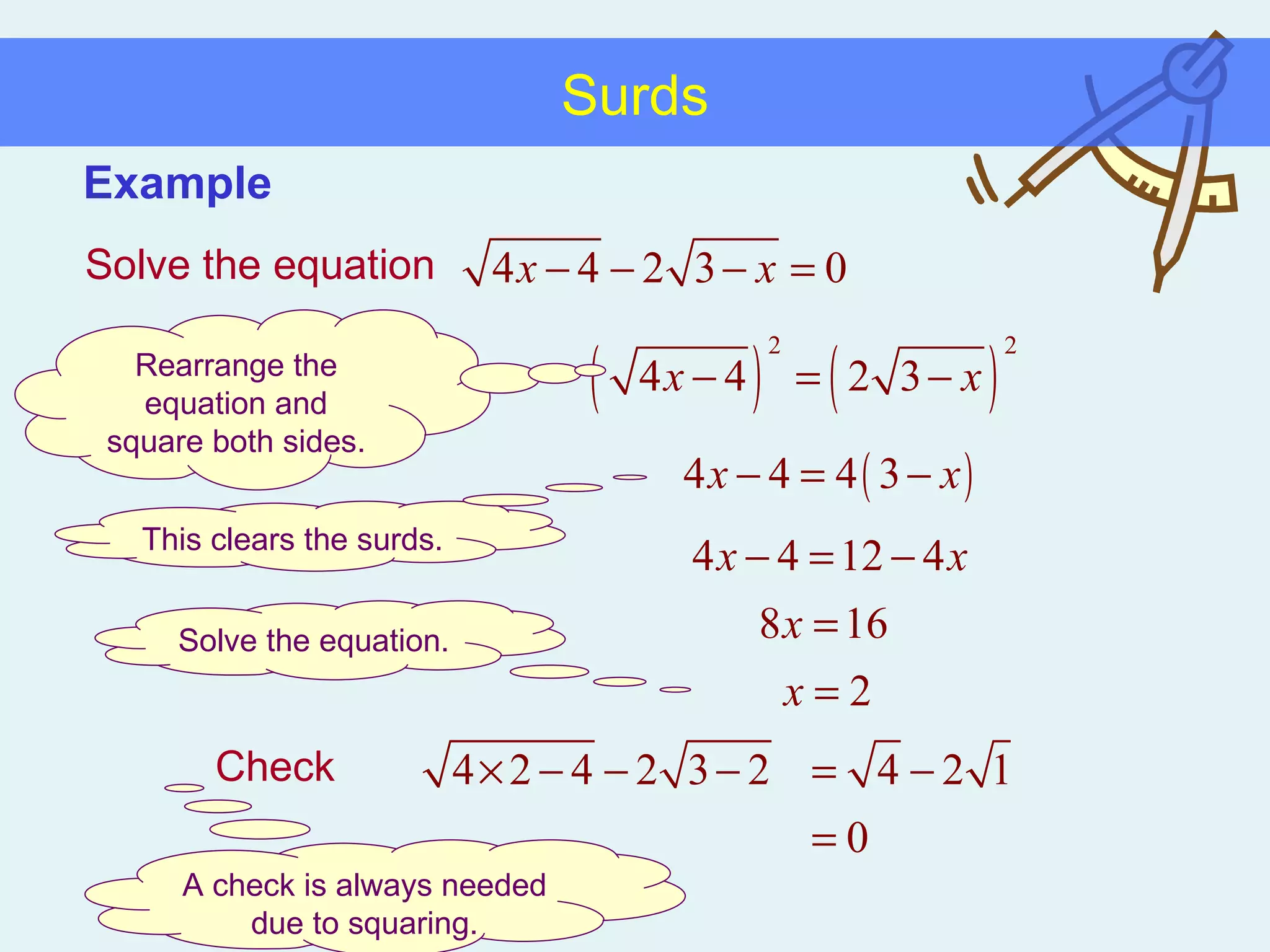
This document discusses working with surds, which are expressions involving square roots. It provides rules for multiplying, dividing, adding, subtracting, and simplifying surds. Some key rules covered are combining like terms under a square root, rationalizing denominators by multiplying the numerator and denominator by the conjugate of the denominator, and squaring both sides of an equation to clear surds before solving. Examples are provided to demonstrate applying these rules to simplify expressions and solve equations involving surds.

1. Surds Surds Objectives In this lesson, we will learn to multiply, divide, add and subtract surds, simplify expressions with surds, rationalise a fraction whose denominator is a surd, solve equations involving surds.

2. is the positive square root of k , for positive values of k . The following rules apply: Let’s apply these rules to simplifying some expressions. Surds

3. Surds Simplify Simplify Combine the square roots. Example

4. Surds Simplify Simplify Applies to the product of any number of terms. Example

5. Surds Simplify Example

6. Surds Simplify Simplify Factorise. Factorise. Example Express each term in terms of

7. Surds Simplify Expand. Collect terms. Example

8. Surds Simplify Rationalise the denominator. Equivalent form Equivalent to multiplying by 1. Example

9. Surds Simplify Equivalent to multiplying by 1. Difference of two squares. Alternate form of the answer. This will rationalise the denominator. Example

10. Surds, Indices and Logarithms Simplify Equivalent to multiplying by 1. Rationalise the denominator. Example

11. Surds, Indices and Logarithms Solve the equation Check Square both sides of the equation. This clears the surds. Example

12. Surds, Indices and Logarithms Summary 1: Rationalising the Denominator You can swap the ‘ –’ and the ‘+’ signs. If the denominator contains Multiply by If the denominator contains Multiply by

13. Surds Solve the equation Check Rearrange the equation and square both sides. This clears the surds. Solve the equation. A check is always needed due to squaring. Example

14. If we square both sides of an equation then the following can happen: So, solving the equation may give us a different solution. Obviously both cannot be correct. Surds . . ,

15. Another rule to apply to the equality of surds Let’s apply this rule to solving an equation. Surds

16. Find the values of a and b . Equating rational and irrational terms. Solve like solving a pair of simultaneous equations. Expand LHS. Surds Example Solution