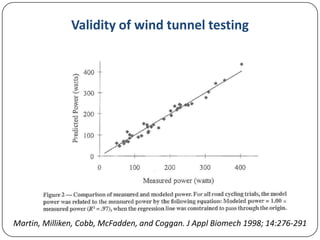
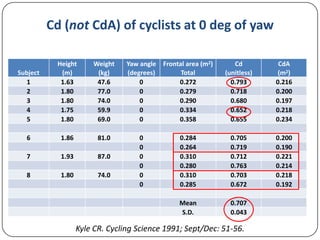
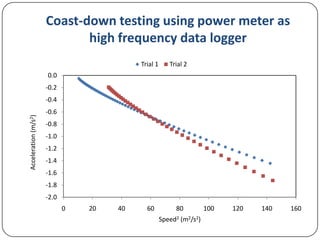
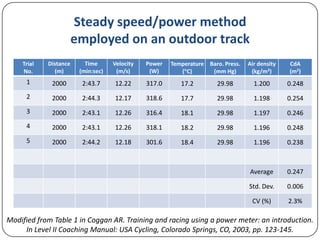
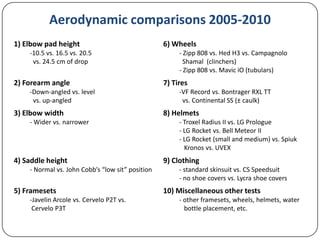
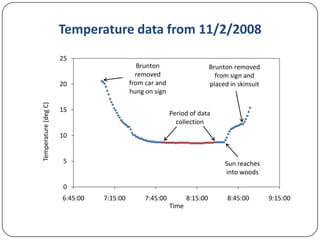
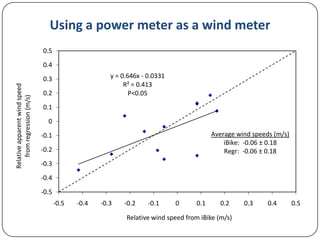
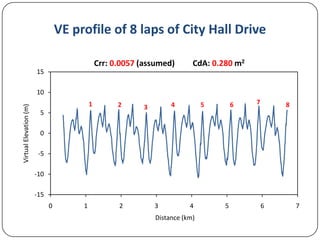
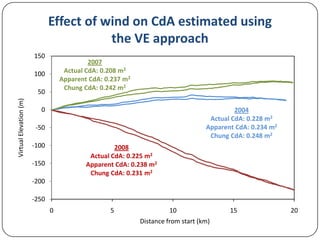
This document discusses various methods for measuring cyclist aerodynamics without using a wind tunnel. It describes taking photographs to measure frontal area, coast-down testing on hills or tracks to determine drag coefficients, and steady-speed power meter methods to differentiate aerodynamic drag and rolling resistance. It provides examples of using these field methods on cyclists and compares the results to wind tunnel data. Specifically, frontal area photography found a mean drag coefficient of 0.707, while coast-down and power meter regression analyses estimated drag values within 1% of wind tunnel tests.

1. Aerodynamic testing without a wind
tunnel: from the simple to the sublime
Andrew R. Coggan, Ph.D.

2. Outline of talk
 Wind tunnel testing/the physics of cycling
 Alternatives to wind tunnel testing

3. Wind tunnel testing: how do you do it?

4. Wind tunnel testing:
advantages and disadvantages
 Advantages
 Accuracy
 Precision/sensitivity
 Speed
 Ability to test at multiple
yaw angles
 Disadvantages
 Cost!

5. CdA as a function of yaw angle
0.250
CdA (m2)
0.200
0.150
Std aero position
Superman position
0.100
0.050
0.000
0
5
10
Yaw angle (deg)
15

6. Validity of wind tunnel testing
Martin, Milliken, Cobb, McFadden, and Coggan. J Appl Biomech 1998; 14:276-291

7. Mathematical model of the physics of cycling
PTOT = (PAT + PKE + PRR + PWB + PPE)/Ec
PTOT = (0.5ρVa2Vg(CdA + Fw) + 0.5(mt + I/r2)(Vgf2 - Vgi2)/(tf - ti) + VgCrrmtgCOS(TAN-1(Gr)) +
Vg(0.091+0.0087Vg) + VgmtgSIN(TAN-1(Gr)))/Ec
Where:
PTOT = total power required (W)
PAT = power required to overcome total aerodynamic drag (W)
PKE = power required to change kinetic energy (W)
PRR = power required to overcome rolling resistance (W)
PWB = power required to overcome drag of wheel bearings (W)
PPE = power required to change potential energy (W)
ρ = air density (kg/m3)
Va = air velocity (relative to direction of travel) (m/s)
Vg = ground velocity (m/s)
Cd = coefficient of drag (dependent on wind direction) (unitless)
A = frontal area of bike+rider system (m2)
FW = wheel rotation factor (expressed as incremental frontal area) (m2)
mt= total mass of bike+rider system (kg)
I = moment of inertia of wheels (kgm2)
r = outside radius of tire (m)
Vgf = final ground velocity (m/s)
Vgi = initial ground velocity (m/s)
tf = final time (s)
ti = initial (s)
Crr = coefficient of rolling resistance (unitless)
g = acceleration due to gravity (9.81 m/s2)
Gr = road gradient (unitless)
Ec = efficiency of chain drive system (unitless)
Martin, Milliken, Cobb, McFadden, and Coggan. J Appl Biomech 1998; 14:276-291

8. Alternatives to wind tunnel testing
 Methods not requiring a power meter
 Frontal area measurements from photographs
 Coast-down testing
 Methods requiring a power meter
 Steady speed/power
 “Classical” regression method
 Robert Chung’s virtual elevation method
 Adam Haile’s short track regression method

9. Measuring frontal area: how do you do it?
Kyle CR. Cycling Science 1991; Sept/Dec: 51-56.

10. Frontal area measurements: advantages and
disadvantages
 Advantages
 Easy
 Inexpensive (free)
 Disadvantages
 Only provides a value for
A, not CdA

11. Cd (not CdA) of cyclists at 0 deg of yaw
Subject
1
2
3
4
5
Height
(m)
1.63
1.80
1.80
1.75
1.80
Weight
(kg)
47.6
77.0
74.0
59.9
69.0
Yaw angle
(degrees)
0
0
0
0
0
Frontal area (m2)
Total
0.272
0.279
0.290
0.334
0.358
Cd
(unitless)
0.793
0.718
0.680
0.652
0.655
CdA
(m2)
0.216
0.200
0.197
0.218
0.234
6
1.86
81.0
7
1.93
87.0
8
1.80
74.0
0
0
0
0
0
0
0.284
0.264
0.310
0.280
0.310
0.285
0.705
0.719
0.712
0.763
0.703
0.672
0.200
0.190
0.221
0.214
0.218
0.192
Mean
S.D.
0.707
0.043
Kyle CR. Cycling Science 1991; Sept/Dec: 51-56.

12. Relationship of CdA to frontal area
0.250
0.200
y = 0.380x + 0.096
R² = 0.595
CdA (m2)
0.150
0.100
0.050
0.000
0.000
0.100
0.200
Frontal area (m2)
0.300
Kyle CR. Cycling Science 1991; Sept/Dec: 51-56.
0.400

13. Cd of model rockets
DeMar JS. National Asssociation of Rocketry Report NAR52094, July 1995.

14. Coast-down testing: how do you do it?
Method 1: coast down a long, steady hill and
record either time or maximal speed.
Method 2: coast down from a higher to a lower
speed on a constant (flat) grade and record rate of
decelleration.

15. Coast-down testing
 Advantages
 Can be inexpensive
(free)
 Disadvantages
 Requires idealized
venue and weather
conditions
 Can be difficult to
achieve high precision
 Time-consuming

16. Coast-down testing: indoors
CV across 4 trials for CdA: 0.56% (n = 30 per trial)
CV across 4 trials for Crr: 0.59% (n = 30 per trial)
CV across 4 trials for CdA: 1.16% (n = 15 per trial)
CV across 4 trials for Crr: 1.83% (n = 15 per trial)
Candau et al. Med Sci Sports Exerc 1999; 31:1441-1447.

17. Coast-down testing: outdoors
CV across 12 trials for CdA: 9.2%
CV across 12 trials for Crr: 138%
Cameron. Human Power 1995; 12:7-11

18. Coast-down testing using power meter as
high frequency data logger
Trial 1
Trial 2
14
12
Speed (m/s)
10
8
6
4
2
0
0
10
20
30
Time (s)
40
50
60

19. Coast-down testing using power meter as
high frequency data logger
Trial 1
Trial 2
60
80
0.0
-0.2
Acceleration (m/s2)
-0.4
-0.6
-0.8
-1.0
-1.2
-1.4
-1.6
-1.8
-2.0
0
20
40
Speed2 (m2/s2)
100
120
140
160

20. Steady speed/power method:
how do you do it?
Ride at a steady speed (or power) on a constant
(flat) grade while recording average power (or
average speed).

21. Steady speed/power method
 Advantages
 Data analysis is simple
 Disadvantages
 Requires idealized
venue and weather
conditions
 Does not differentiate
between Crr and CdA

22. Steady speed/power method
employed on an outdoor track
Trial
No.
Distance
(m)
Time
(min:sec)
Velocity
(m/s)
Power
(W)
1
2000
2:43.7
12.22
317.0
17.2
2
2000
2:44.3
12.17
318.6
3
2000
2:43.1
12.26
4
2000
2:43.1
5
2000
2:44.2
Temperature Baro. Press.
(mm Hg)
(C)
Air density
(kg/m3)
CdA
(m2)
29.98
1.200
0.248
17.7
29.98
1.198
0.254
316.4
18.1
29.98
1.197
0.246
12.26
318.1
18.2
29.98
1.196
0.248
12.18
301.6
18.4
29.98
1.196
0.238
Average
0.247
Std. Dev.
0.006
CV (%)
2.3%
Modified from Table 1 in Coggan AR. Training and racing using a power meter: an introduction.
In Level II Coaching Manual: USA Cycling, Colorado Springs, CO, 2003, pp. 123-145.

23. “Classical” regression method:
how do you do it?
Ride at a range of steady speeds on a constant (flat)
grade while recording average power (and speed).

24. “Classical” regression method
 Advantages
 Disadvantages
 High accuracy and
 Time-consuming
precision attainable
 Differentiates between
CdA and Crr (mu)
 Requires idealized
venue and weather
conditions

25. Accuracy of the regression approach
Subject
Wind tunnel
CdA (m2)
Field test
CdA (m2)
Difference
(m2)
Difference
(%)
1
0.247
0.252
+0.005
+2.0%
2
0.291
0.269
-0.022
-7.6%
3
0.240
0.241
+0.001
+0.4%
4
0.251
0.251
0.000
0.0%
5
0.252
0.253
+0.001
+0.4%
6
0.285
0.283
-0.002
-0.7%
7
0.198
0.198
0.000
0.0%
Mean
0.252
0.250
-0.002
-0.8%
S.D.
0.031
0.027
0.009
3.1%
Data for subjects 1-6 are from Martin JC et al. Med Sci Sports Exerc 2006; 38:592-597,
whereas data for subject 7 are unpublished observations of the presenter.

26. Taking the Tom Compton challenge:
the experiment

27. Taking the Tom Compton challenge: results
Expected
Measured
Difference in aerodynamic drag (N)
0.35
0.30
0.25
0.20
0.15
0.10
0.05
0.00
6.4 cm sphere
10.2 cm sphere

28. Determination of Crr via regression testing
Crr from Andy's field tests (regression method)
0.0060
y = 1.087x + 0.000
R² = 0.949
Y=X
0.0050
0.0040
0.0030
Continental SS (clinchers)
Continental SS + Bontrager RXL
TT (clinchers)
VF Record (clinchers)
Bontrager RXL TT (clinchers)
Bad cassette
bearings!
0.0020
0.0010
0.0000
0.000 0.001 0.002 0.003 0.004 0.005 0.006
Crr from Al's roller testing
VF Record + Tufo S3 Pro
(tubulars)
Michelin Pro Race 2 SC
(clinchers)
VF Record (tubular) + Vred
Fortezza Tricomp (clincher)
Continental Ultra 2000
(clinchers)
Bontrager RXL TT (clinchers)

29. Aerodynamic comparisons 2005-2010
1) Elbow pad height
-10.5 vs. 16.5 vs. 20.5
vs. 24.5 cm of drop
2) Forearm angle
-Down-angled vs. level
vs. up-angled
3) Elbow width
- Wider vs. narrower
4) Saddle height
- Normal vs. John Cobb’s “low sit” position
5) Framesets
-Javelin Arcole vs. Cervelo P2T vs.
Cervelo P3T
6) Wheels
- Zipp 808 vs. Hed H3 vs. Campagnolo
Shamal (clinchers)
- Zipp 808 vs. Mavic iO (tubulars)
7) Tires
-VF Record vs. Bontrager RXL TT
vs. Continental SS (± caulk)
8) Helmets
- Troxel Radius II vs. LG Prologue
- LG Rocket vs. Bell Meteor II
- LG Rocket (small and medium) vs. Spiuk
Kronos vs. UVEX
9) Clothing
- standard skinsuit vs. CS Speedsuit
- no shoe covers vs. Lycra shoe covers
10) Miscellaneous other tests
- other framesets, wheels, helmets, water
bottle placement, etc.

30. Centaur Road in Chesterfield, MO
The Centaur Road
“natural wind
tunnel”

31. Centaur Road: a “natural wind tunnel”
Photo courtesy of Mark Ewers

32. Temperature data from 11/2/2008
25
Brunton
removed
from car and
hung on sign
Temperature (deg C)
20
15
Brunton removed
from sign and
placed in skinsuit
Period of data
collection
10
5
Sun reaches
into woods
0
6:45:00
7:15:00
7:45:00
8:15:00
Time
8:45:00
9:15:00

33. Beware of local variations
in environmental conditions!
Airport temperature (deg C)
30
25
y = 1.151x - 0.711
R² = 0.952
20
15
10
5
0
0
5
10
15
20
Brunton temperature (deg C)
25
30

34. CdA and Crr determined using the regression
method (non-linear fit)
West
East
450
400
y = 0.1339x2 + 2.924
R² = 0.9989
350
Power (W)
300
250
200
150
CdA = 0.233 ± 0.004 m2
Crr = 0.00387 ± 0.00039
100
50
0
0
2
4
6
8
Speed (m/s)
10
12
14
16

35. CdA and Crr determined using the regression
method (linear fit)
West
East
30
25
y = 0.134x + 2.889
R² = 0.997
Force (N)
20
15
CdA = 0.233 ± 0.003 m2
Crr = 0.00382 ± 0.00029
10
5
0
0
25
50
75
100
Speed2 (m2/s2)
125
150
175
200

36. CdA and Crr determined using the regression
method (worst case scenario)
East
West
30
y = 0.135x + 4.064
R² = 0.941
25
Force (N)
20
15
CdA = 0.232 ± 0.017 m2
Crr = 0.00515 ± 0.00135
10
5
0
0
25
50
75
100
Speed2 (m2/s2)
125
150
175
200

37. CdA and Crr determined using the regression
method (assuming constant wind)
East
West
30
y = 0.1356x + 4.000
R² = 0.9975
25
Force (N)
20
15
CdA = 0.233 ± 0.003 m2
Crr = 0.00506 ± 0.00027
Est. wind = 0.49 m/s
10
5
0
0
25
50
75
100
Speed2 (m2/s2)
125
150
175
200

38. Using a power meter as a wind meter
0.5
0.4
y = 0.646x - 0.0331
R² = 0.413
P<0.05
Relative apparent wind speed
from regression (m/s)
0.3
0.2
0.1
0
Average wind speeds (m/s)
iBike: -0.06 ± 0.18
Regr: -0.06 ± 0.18
-0.1
-0.2
-0.3
-0.4
-0.5
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
Relative wind speed from iBike (m/s)
0.3
0.4
0.5

39. The Beaufort scale

40. Wind is thine enemy!!

41. Robert Chung’s “virtual elevation” (VE)
method: how do you do it?
The VE method is really more of a post-hoc analytical
approach than it is a formal means of performing field tests.
Typically, however, it applied to data collected while riding
out-and-back along the same stretch of road or around and
around the same loop, while allowing speed and power to vary.
Changes in kinetic and potential energy are then taken into
consideration in the calculations, leveraging the knowledge
that the same point on the road is always at the same elevation
to calculate a “virtual elevation” that reflects the true elevation
plus any unexplained variability due to, e.g., wind.

42. Robert Chung’s VE method
 Advantages
 Disadvantages
 Allows use of wider
 Data dropouts can be a
variety of venues
 Often faster than
regression testing
 High precision attainable
PITA
 Can often be difficult to
differentiate between Δ in
CdA and Δ in Crr (mu)
 Accuracy?
 Does not account for wind

43. City Hall Drive in Ballwin, MO

44. Speed, power, and virtual elevation during a
representative lap of City Hall Drive
Speed (m/s)
Virtual elevation (m)
Power (W)
500
10
400
5
300
0
200
-5
100
-10
-15
0
3.15
3.35
3.55
Distance (km)
3.75
3.95
Power (W)
Speed (m/s) or virtual Elevation (m)
15

45. VE profile of 8 laps of City Hall Drive
Crr: 0.0038 (assumed)
CdA: 0.305 m2
15
Virtual Elevation (m)
10
1
2
4
3
5
5
6
7
8
0
-5
-10
-15
0
1
2
3
4
Distance (km)
5
6
7

46. VE profile of 8 laps of City Hall Drive
Crr: 0.0057 (assumed)
CdA: 0.280 m2
15
Virtual Elevation (m)
10
1
2
5
4
3
5
6
7
8
0
-5
-10
-15
0
1
2
3
4
Distance (km)
5
6
7

47. VE profile of 8 laps of City Hall Drive
Crr: 0.0019 (assumed)
CdA: 0.331 m2
15
Virtual Elevation (m)
10
1
2
5
4
3
5
6
7
8
0
-5
-10
-15
0
1
2
3
4
Distance (km)
5
6
7

48. Effect of wind on CdA estimated using
the VE approach
150
2007
Actual CdA: 0.208 m2
Apparent CdA: 0.237 m2
Chung CdA: 0.242 m2
100
Virtual Elevation (m)
50
0
2004
Actual CdA: 0.228 m2
Apparent CdA: 0.234 m2
Chung CdA: 0.248 m2
-50
-100
2008
Actual CdA: 0.225 m2
Apparent CdA: 0.238 m2
Chung CdA: 0.231 m2
-150
-200
-250
0
5
10
Distance from start (km)
15
20

49. Wind is thine enemy!!

50. Adam Haile’s short track regression method:
method: how do you do it?
Similar to the classical regression approach, Crr and CdA are
derived by regressing force on velocity. However, rather than
utilizing average values obtained during each “run”, the short
track regression method uses each lap-length segment of data
extractable from multiple short laps. Since each lap starts and
ends in the same place (at least theoretically), variations in
potential energy can be ignored. On the other hand, speed is
allowed to vary within laps (and must vary across laps), with
variations in kinetic energy accounted for in the calculations

51. Adam Haile’s
short track regression method
 Advantages
 Disadvantages
 High precision
 Data dropouts can be a
attainable
 Differentiates between
CdA and Crr (mu)
 Allows use of wider
variety of venues
 Faster than regression
testing (?)
PITA
 Accuracy?
 Does not account for
wind

52. Example data from short track regression
testing on an indoor track

53. Summary and conclusions
 A wide variety of methods exist for estimating CdA
without use of a wind tunnel. Each has its advantages
and disadvantages, with the quality of the data
depending more upon attention to detail and
access/selection of an appropriate test venue than
upon the exact method used. The best choice will
therefore depend upon an individual’s specific
circumstances.