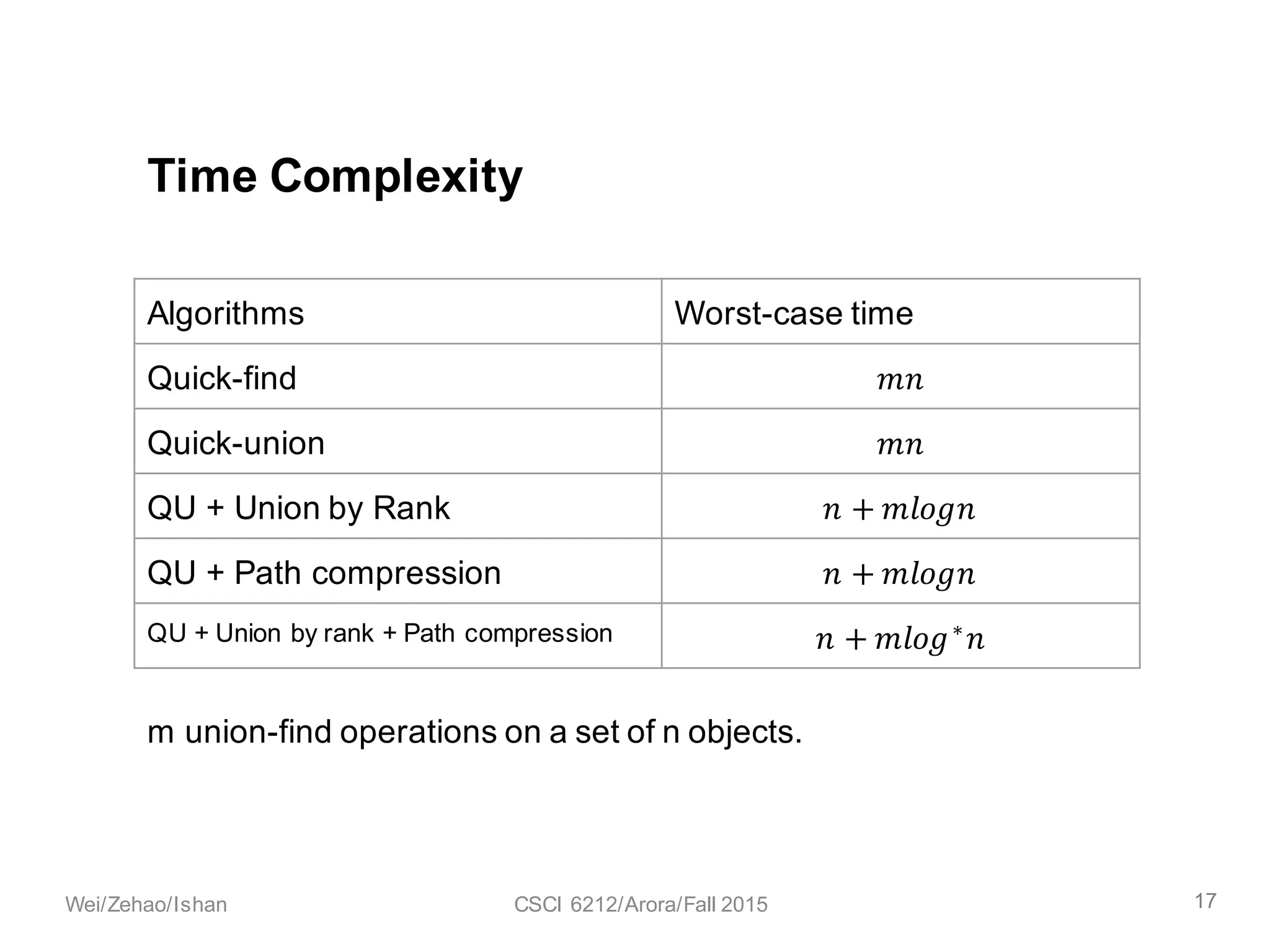
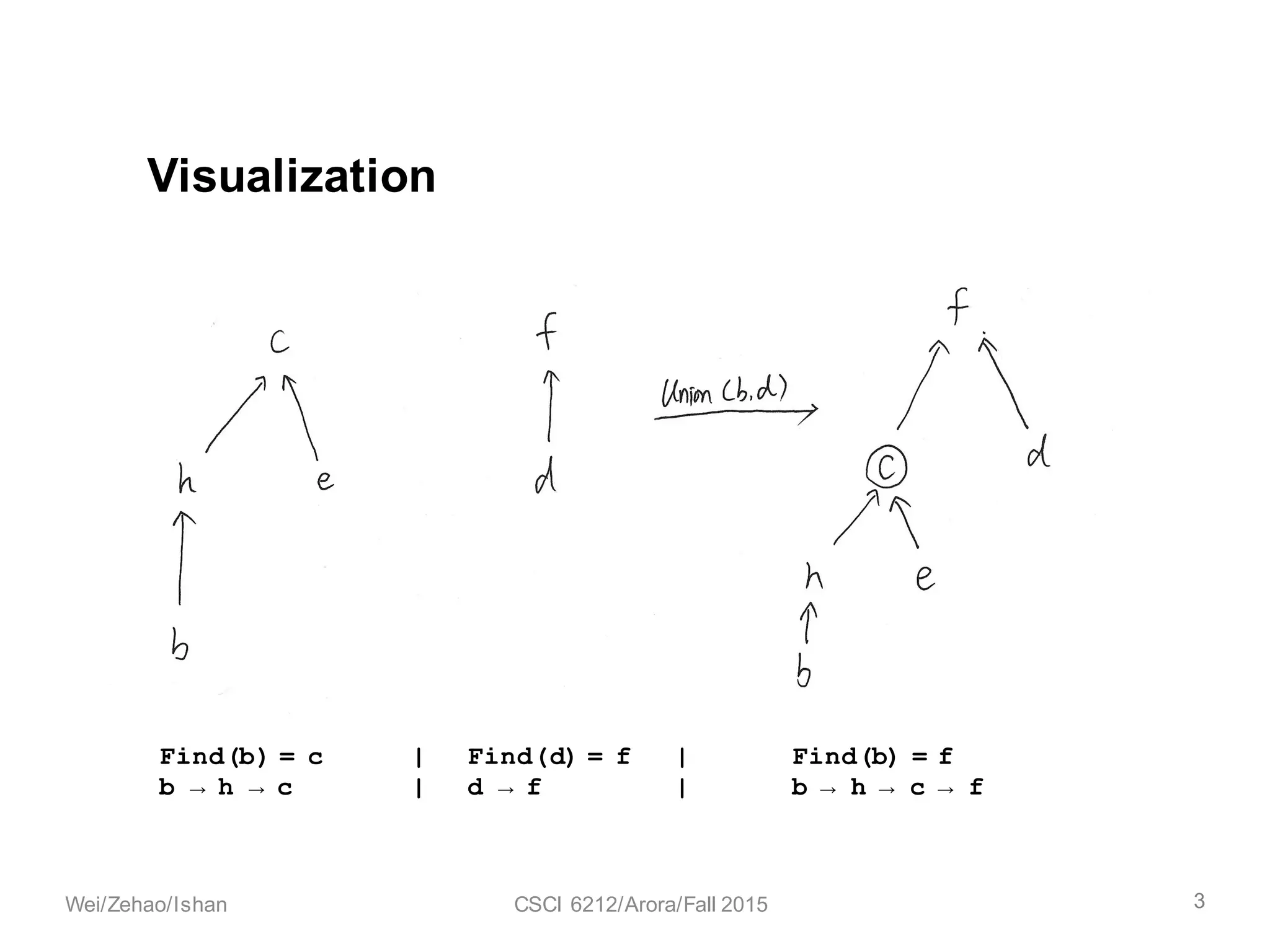
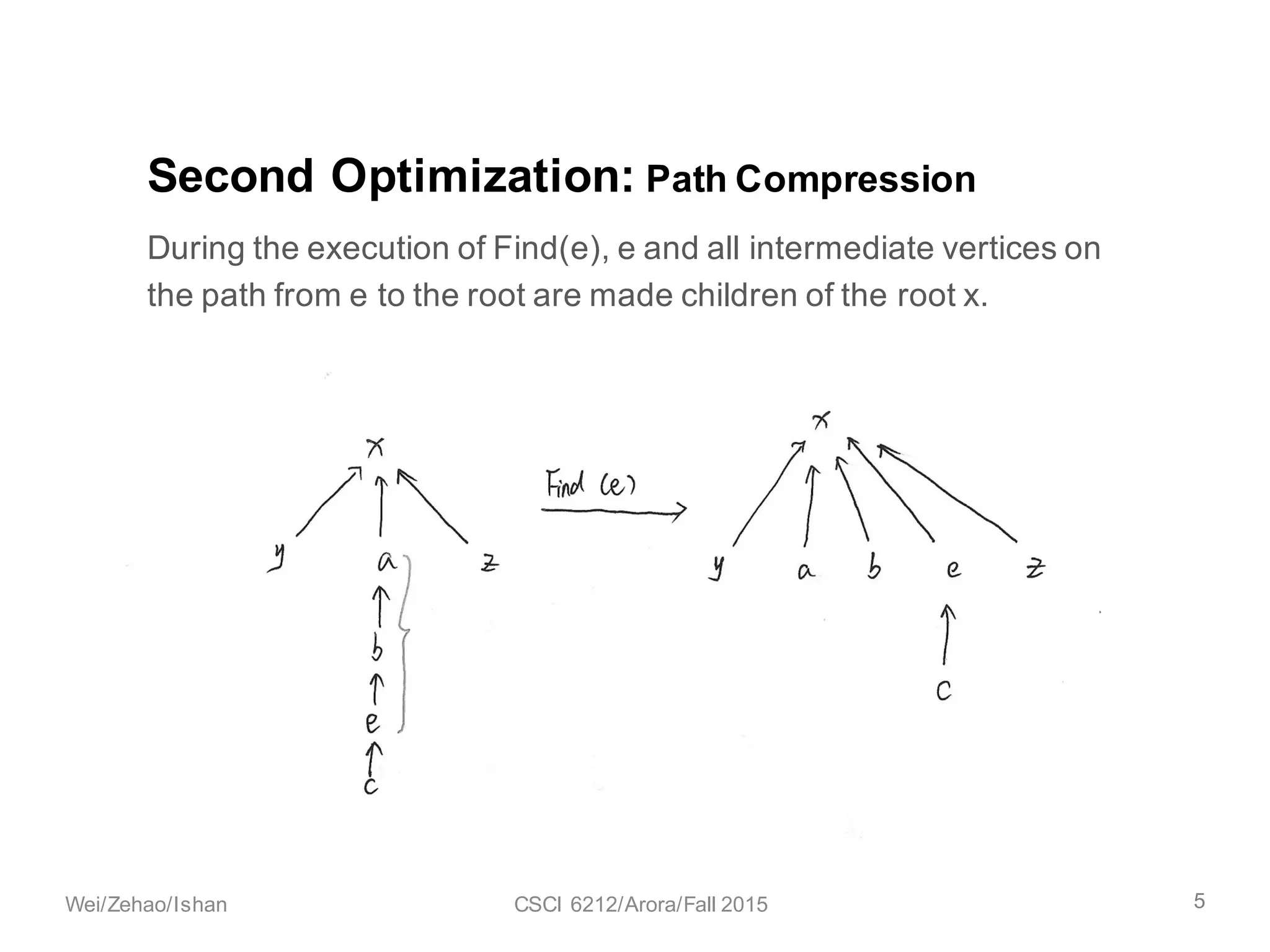
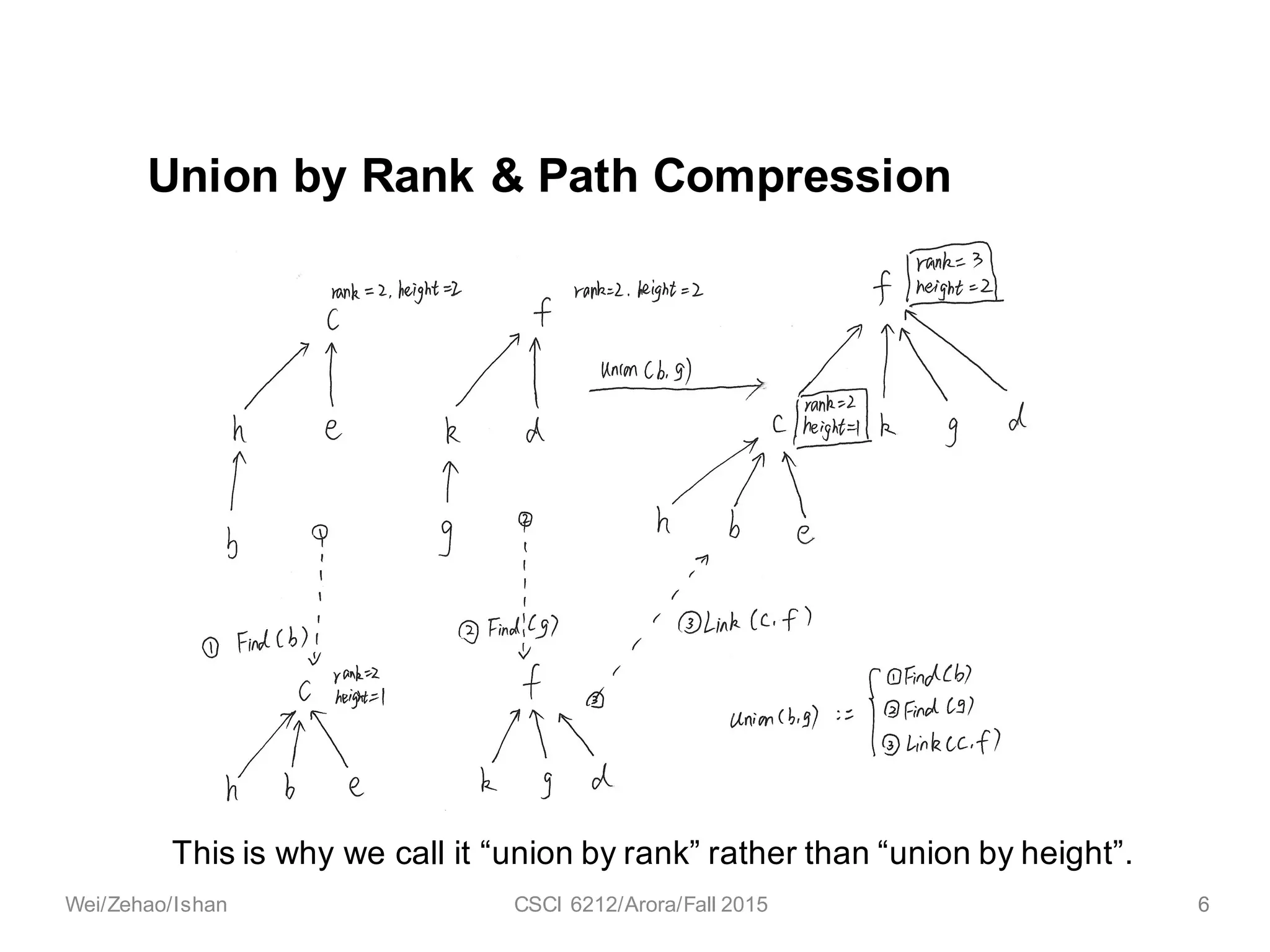
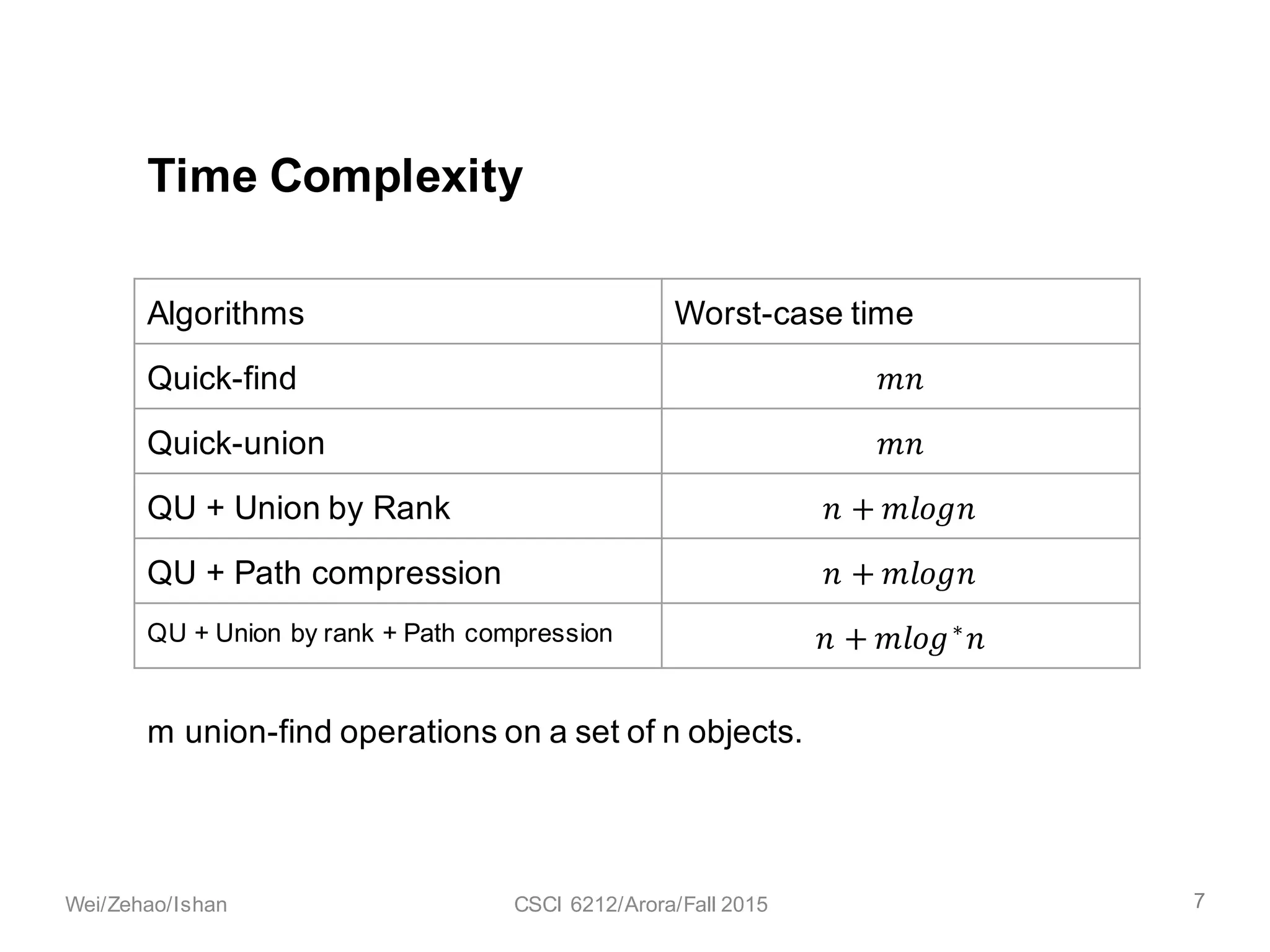
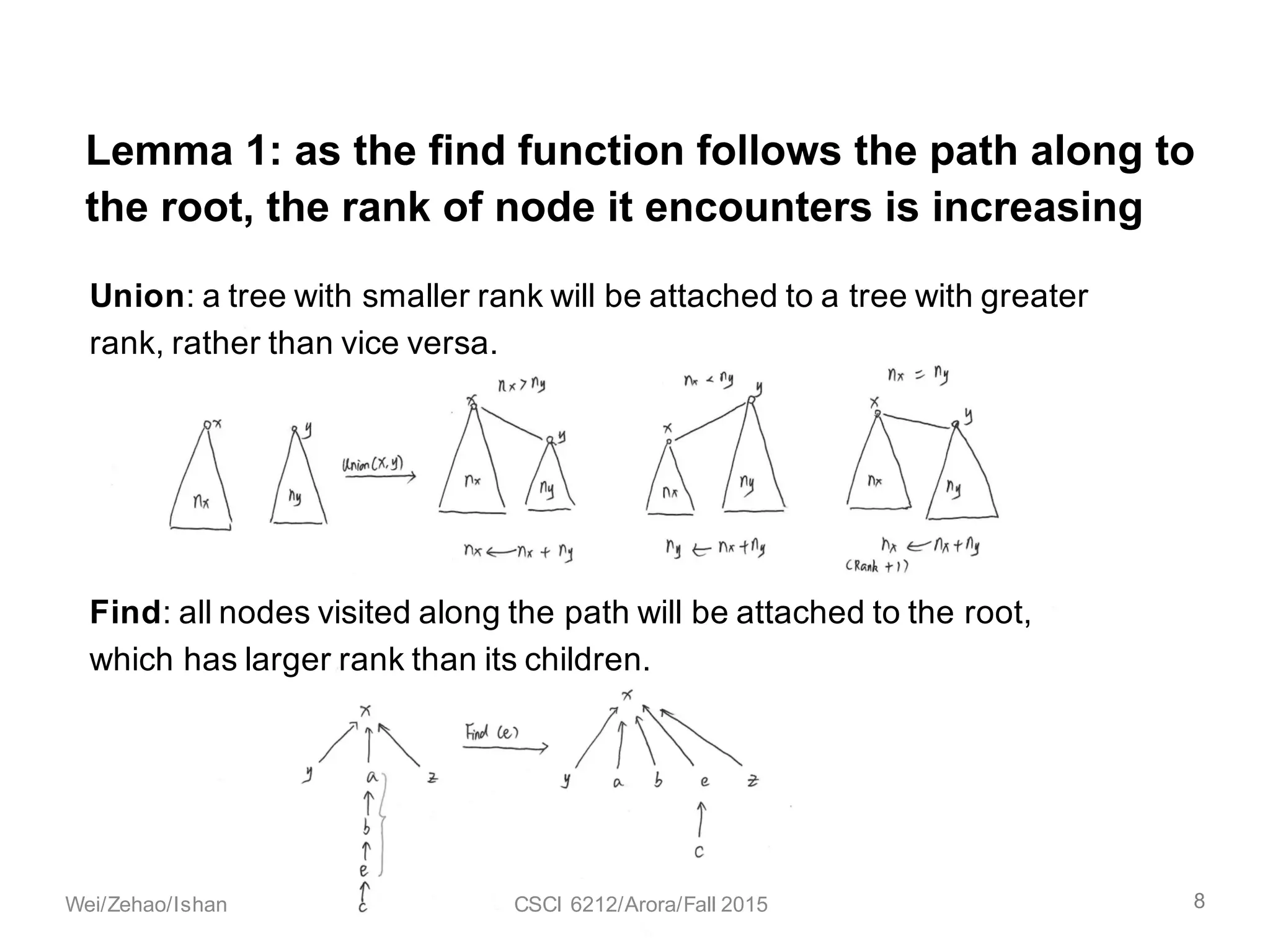
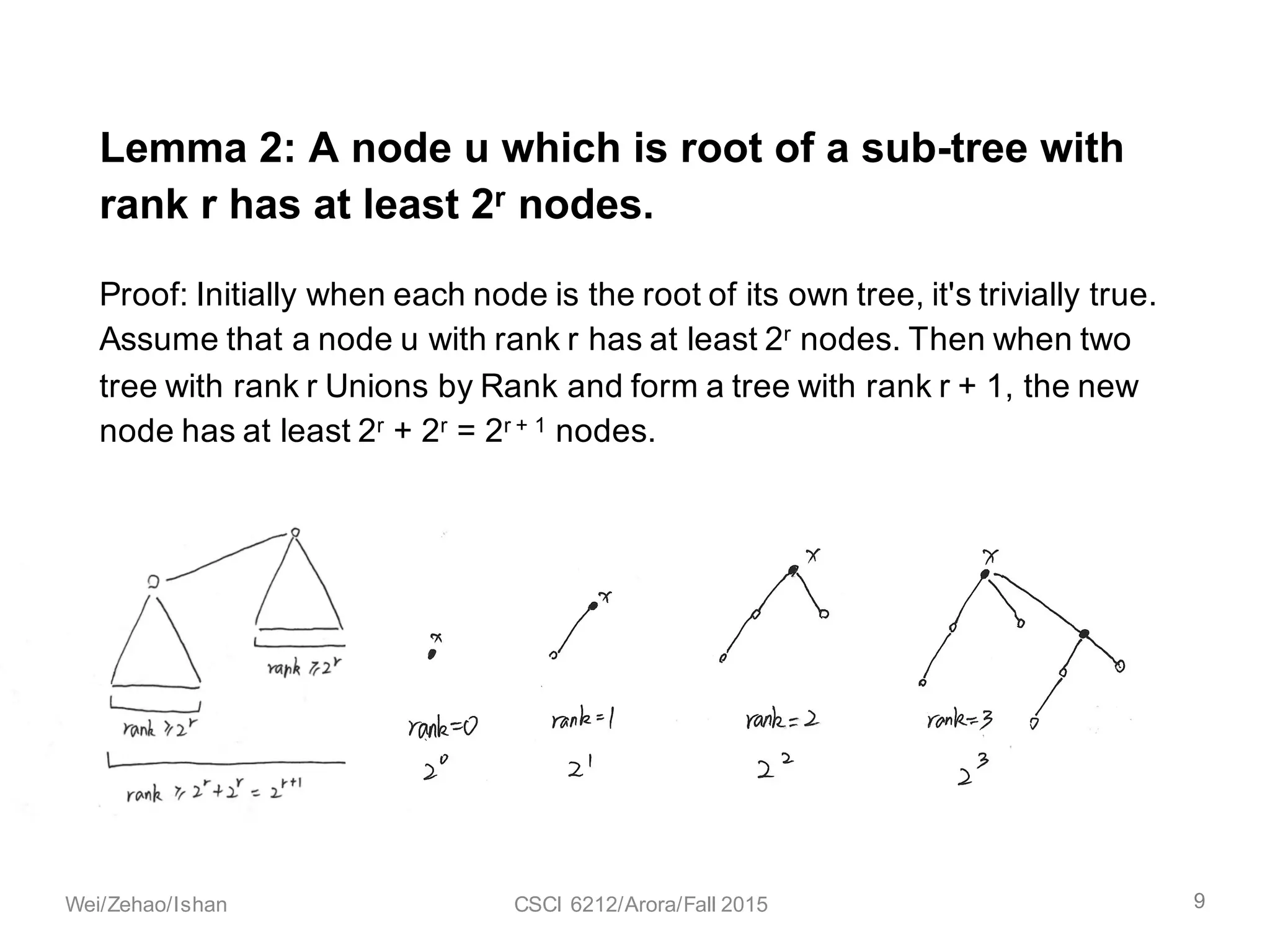
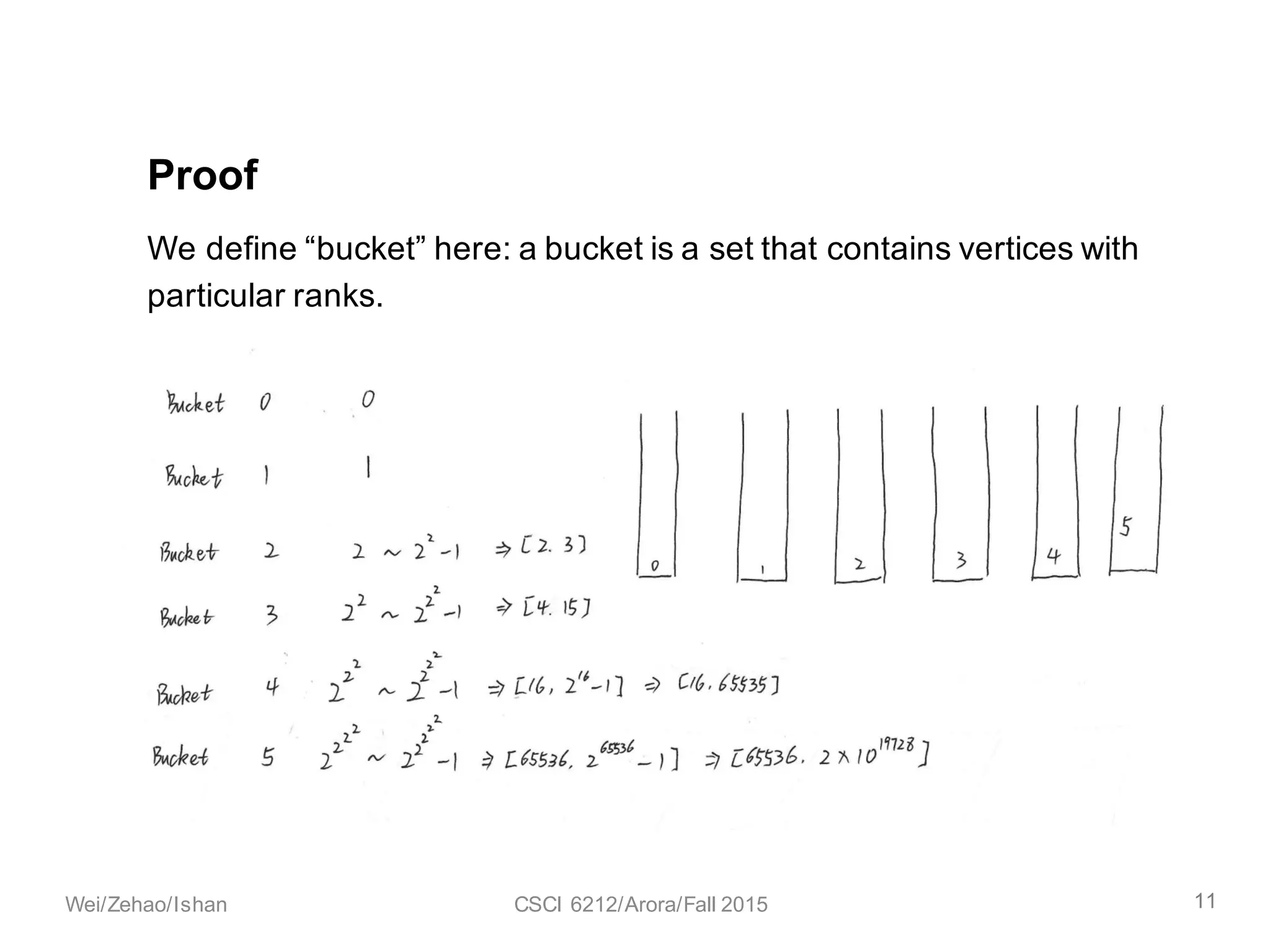
The document discusses the union find algorithm and its time complexity. It defines the union find problem and three operations: MAKE-SET, FIND, and UNION. It describes optimizations like union by rank and path compression that achieve near-linear time complexity of O(m log* n) for m operations on n elements. It proves several lemmas about ranks and buckets to establish this time complexity through an analysis of the costs T1, T2, and T3.





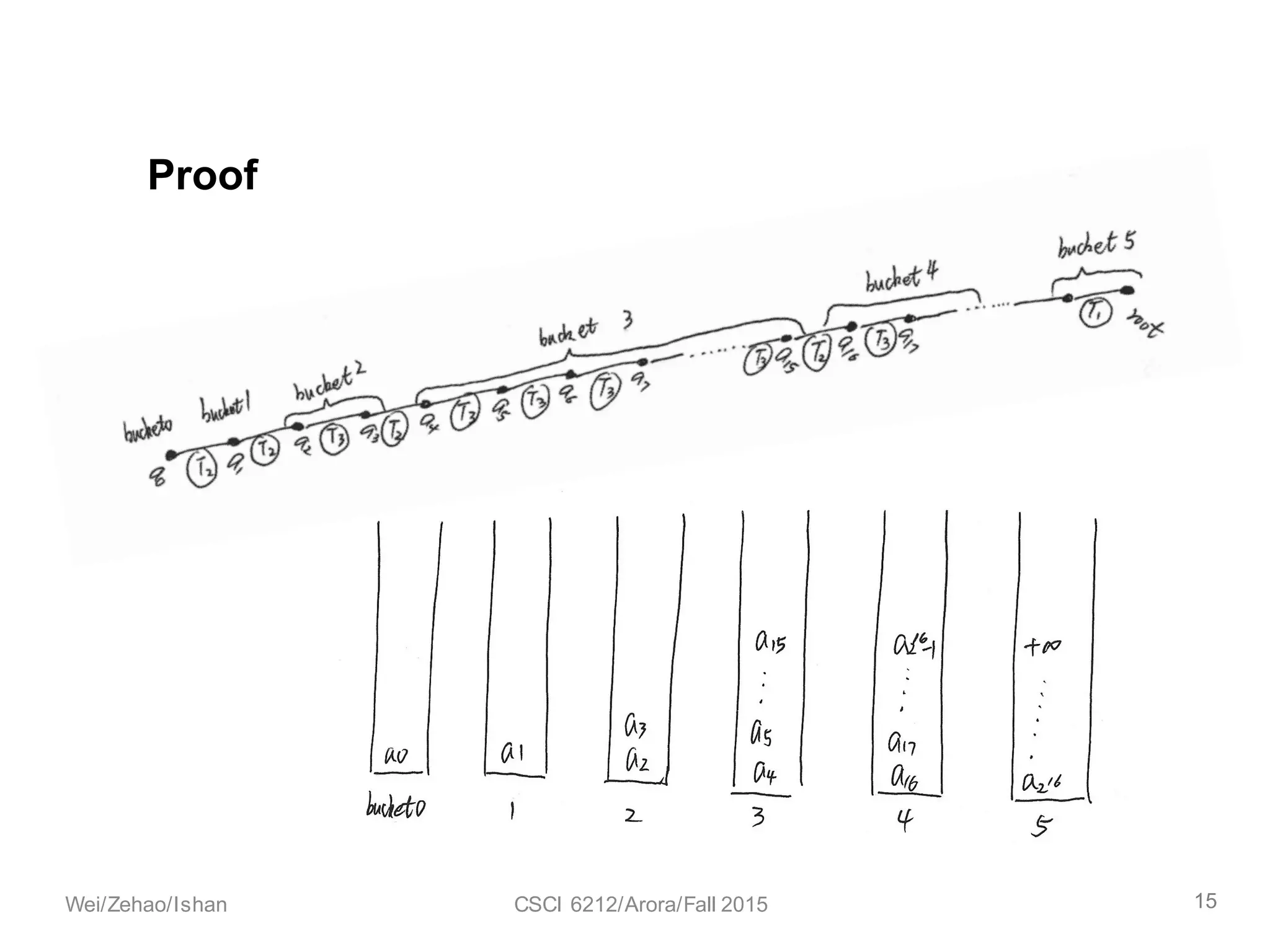
![We can make two observations about the buckets.
The total number of buckets is at most 𝒍𝒐𝒈∗ 𝒏.
Proof: When we go from one bucket to the next, we add one more two
to the power, that is, the next bucket to [B, 2B − 1] will be [2C
,2<E
− 1 ]
The maximum number of elements in bucket [B, 2B – 1] is at
most 𝒏.
Proof: The maximum number of elements in bucket [B, 2B – 1] is at
most 𝑛 2 𝐵⁄ + 𝑛 2CI9⁄ + 𝑛 2CI<⁄ + ⋯ + 𝑛 2<EK9
≤ 2 𝐵 − 1 − 𝐵 ∗ 𝑛/2 𝐵⁄ ≤ n
Proof
13Wei/Zehao/Ishan CSCI 6212/Arora/Fall 2015](https://image.slidesharecdn.com/timecomplexityofunionfind-151206023623-lva1-app6892/75/Time-complexity-of-union-find-13-2048.jpg)