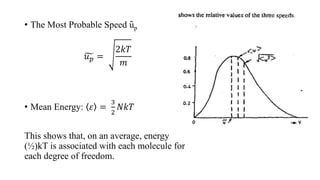
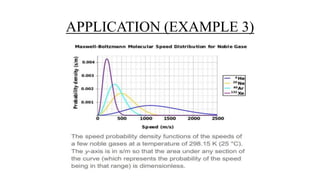
The document discusses the Maxwell-Boltzmann velocity distribution, covering its introduction, derivation, and application examples. It explores kinetic theory, probability assumptions, and provides mathematical expressions for momentum and energy distributions in gases. Applications include calculating the root mean square speed and effective temperature of gas particles based on their velocities.

1. Maxwell Boltzmann Velocity Distribution
Vishwajeet Jadeja
MSc Statistics
Department of Statistics
The Maharaja Sayajirao University of Baroda

2. CONTENTS
• Introduction
• Derivation
• Conclusion
• Application (Example)

3. INTRODUCTION*
• Kinetic Theory of gases.
• The role of probability in Maxwell distribution.
• Assumptions.
• Normal Distribution.
*Follow the reference given in the next slide.

4. DERIVATION
• 𝜓 𝑢2
= 𝜙 𝑢 𝑥
2
. 𝜙 𝑢 𝑦
2
. 𝜙 𝑢 𝑧
2
• 𝑓 𝑢 𝑥 𝑑𝑢 𝑥 = 𝐶. 𝑒−𝛼𝑢 𝑥
2
𝑑𝑢 𝑥
• 𝐶 =
𝛼
𝜋
• 𝑁 𝑢 𝑑𝑢 = 4𝜋𝑁𝑜
𝛼
𝜋
3
2
𝑒−𝛼𝑢2
𝑢2 𝑑𝑢
• 𝛼 =
𝑚
2𝑘𝑇
𝑁 𝑢 𝑑𝑢 = 4𝜋𝑁𝑜
𝑚
2𝜋𝑘𝑇
3
2
𝑒
−𝑚𝑢2
2𝑘𝑇 𝑢2
𝑑𝑢
Please Refer: Pg 35-40, 48. B. B. LAUD, Fundamentals of Statistical Mechanics, New Age
International Publishers. Get it from: www.gen.lib.rus.ec

5. MOMENTUM DISTRIBUTION
• p = mu
𝑁 𝑝 𝑑𝑝 = 4𝜋𝑁𝑜
1
2𝜋𝑚𝑘𝑇
3
2
𝑒
−𝑝2
2𝑚𝑘𝑇 𝑝2 𝑑𝑢
• p ~ Normal Distribution with Variance, 𝑎 = 𝑚𝑘𝑇.

6. ENERGY DISTRIBUTION
• 𝜀 =
1
2
𝑚𝑢2
𝑁 𝜀 𝑑𝜀 =
2𝑁
𝜋
1
𝑘𝑇
3
2
𝑒−𝜀 𝑘𝑇
𝜀1 2
𝑑𝜀
• the energy is proportional to the sum of the squares of the three
Normally Distributed momentum components.

7. SIGNIFICANT MEAN VALUES
• Mean Value of un
𝑢 𝑛 =
2
𝜋
2𝑘𝑇
𝑚
𝑛 2
𝑛 + 3
2
• The Mean Speed <u> is;
𝑢 =
8𝑘𝑇
𝜋𝑚
• Root Mean Square Speed
𝑢2 =
3𝑘𝑇
𝑚

8. • The Most Probable Speed u͂ p
𝑢 𝑝 =
2𝑘𝑇
𝑚
• Mean Energy: 𝜀 =
3
2
𝑁𝑘𝑇
This shows that, on an average, energy
(½)kT is associated with each molecule for
each degree of freedom.

9. CONCLUSION
The expression
𝑁 𝑢 𝑑𝑢 = 4𝜋𝑁𝑜
𝑚
2𝜋𝑘𝑇
3
2
𝑒
−𝑚𝑢2
2𝑘𝑇 𝑢2
𝑑𝑢
giving the mean number of molecules having a velocity between u and u
+ du in a gas at the absolute temperature T. It is merely a special case of
the Normal Distribution.

10. APPLICATION (EXAMPLE 1)
Q. A certain gaseous system contains 16,200 molecules. Each has a
mass of 1.0 x 10-26 kg. Determine vrms and from that, what effective
temperature would the gas have?
No. of Molecules Speed (m/s)
1700 220
4200 490
4900 660
3300 880
1500 1150
600 1400

11. APPLICATION (EXAMPLE 2)
Q. Imagine if there are 20 gas particles in a box.
2 of them are moving at 200 m/s,
3 of them are moving at 220 m/s,
5 of them are moving at 250 m/s,
4 of them are moving at 270 m/s,
3 of them are moving at 290 m/s,
2 of them are moving at 310 m/s,
1 of them are moving at 330 m/s.
Calcutate vp, v̅, vrms.

12. APPLICATION (EXAMPLE 3)

13. Thank You