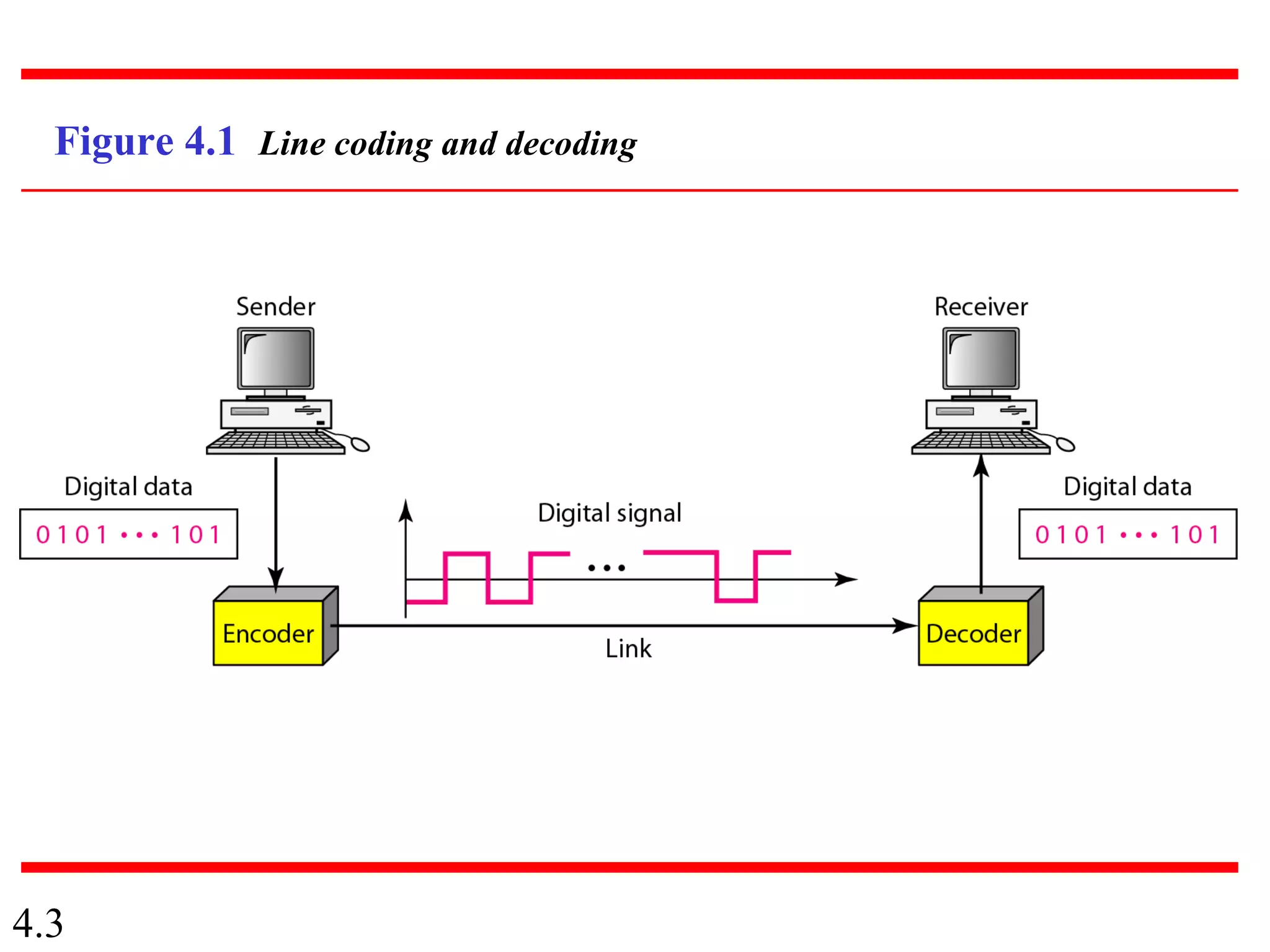
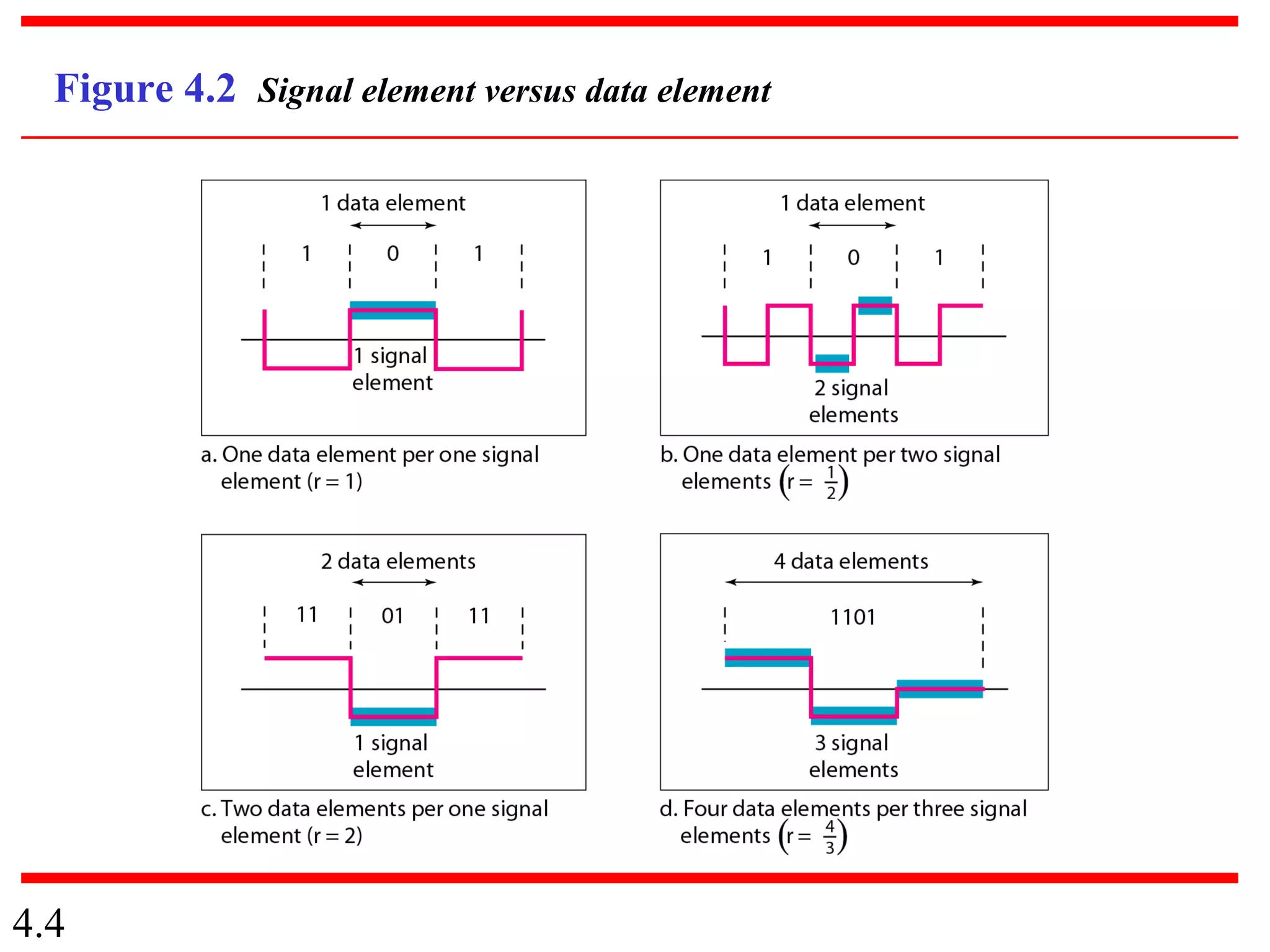
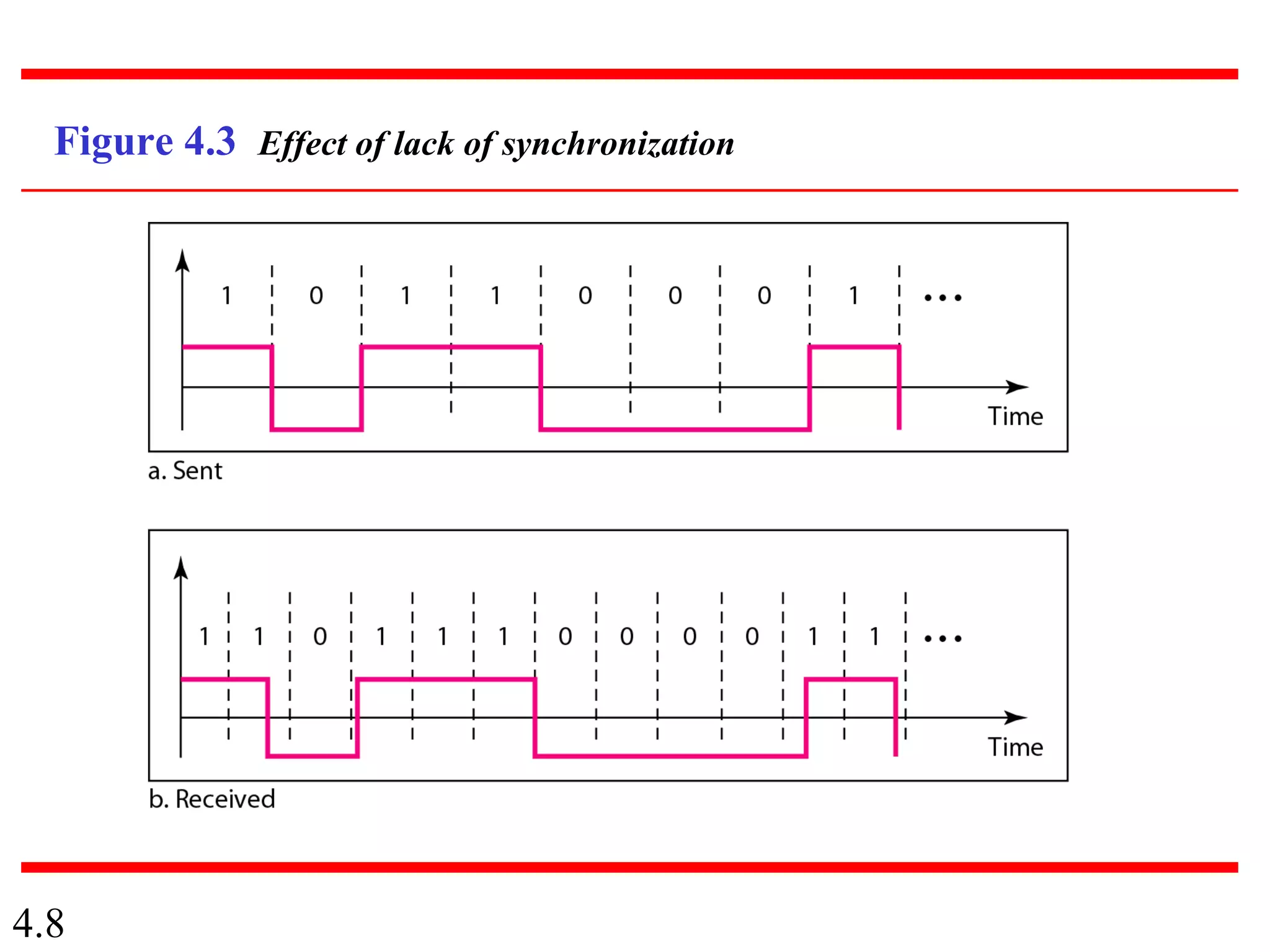
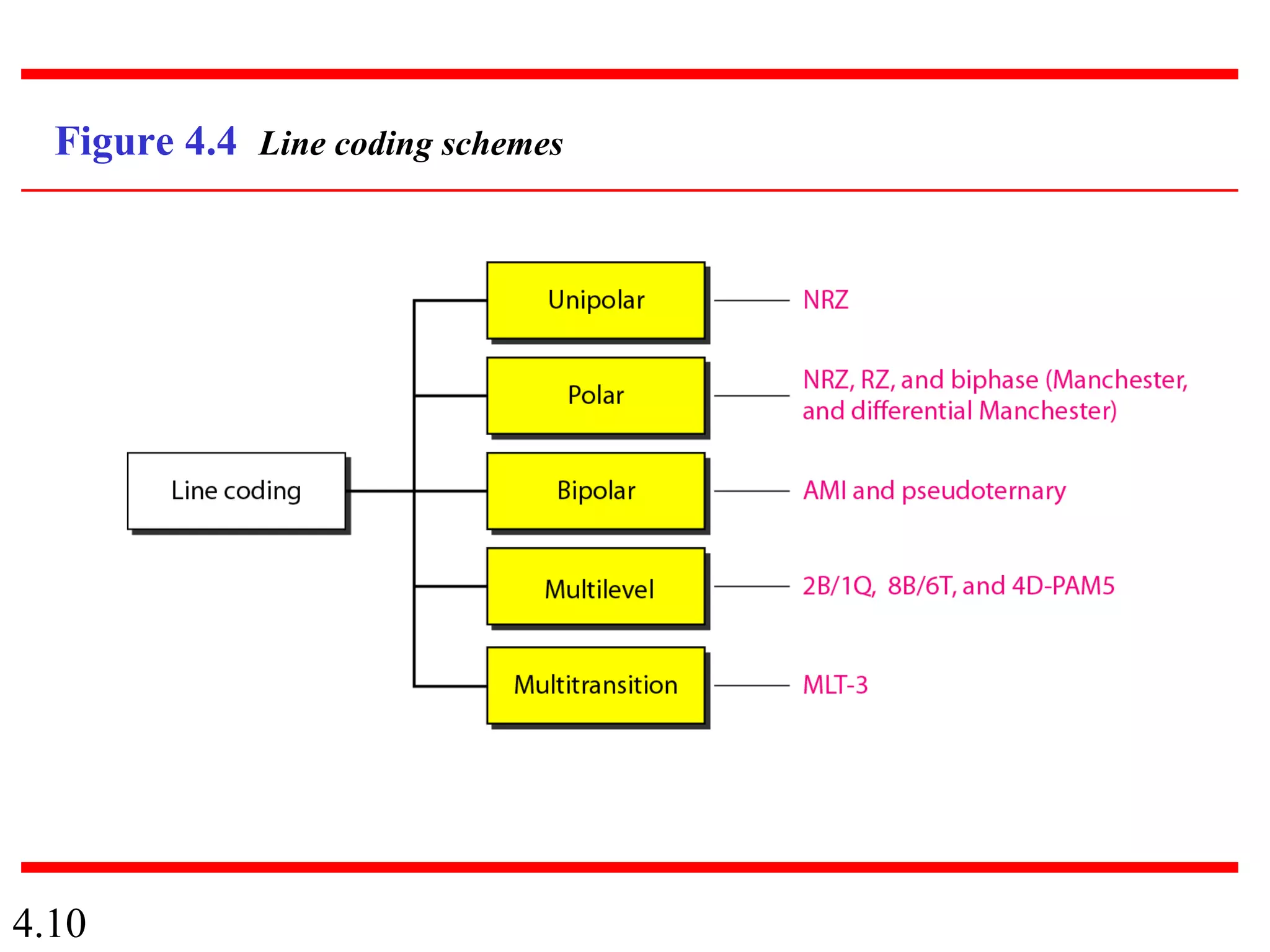
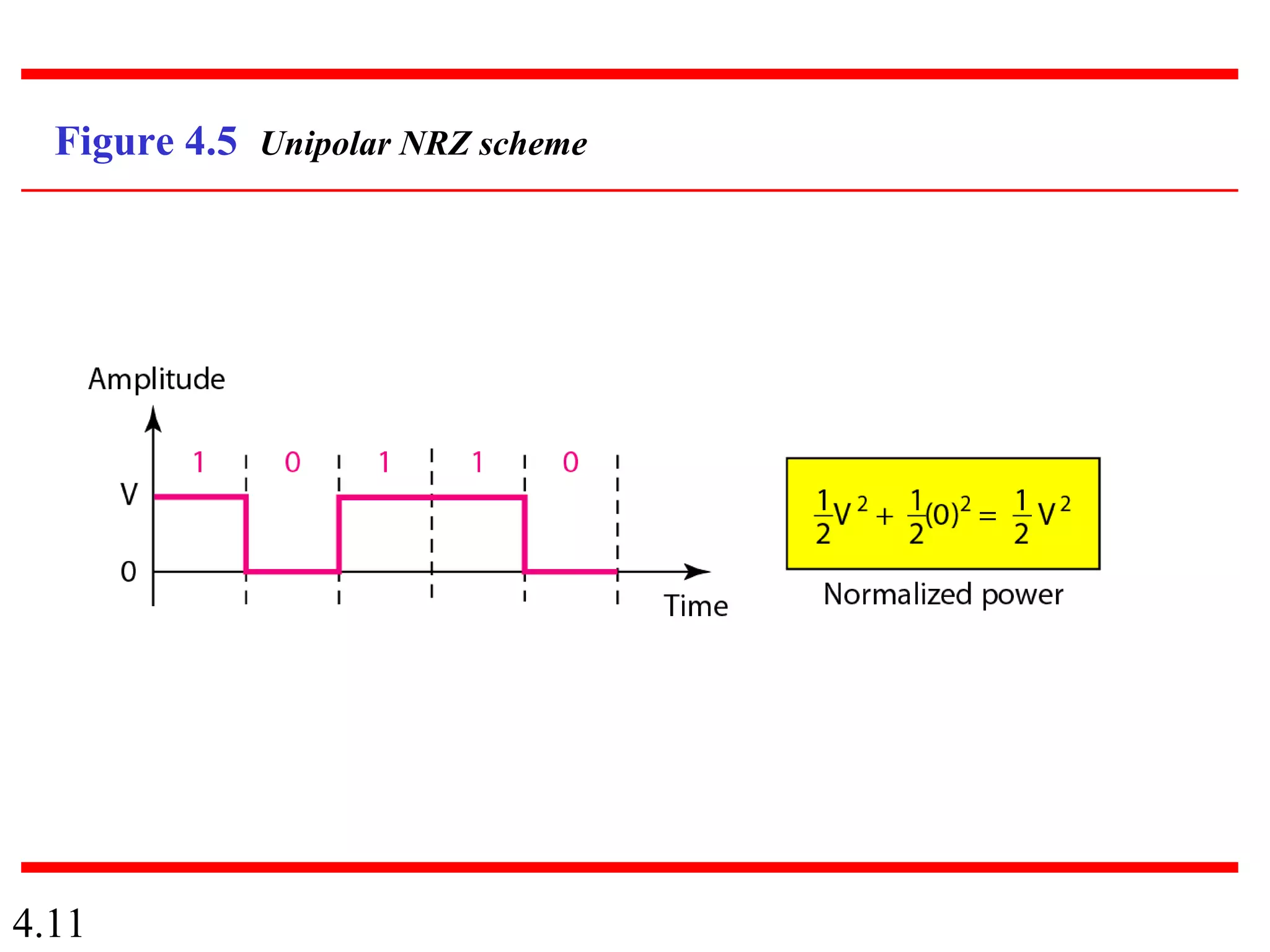
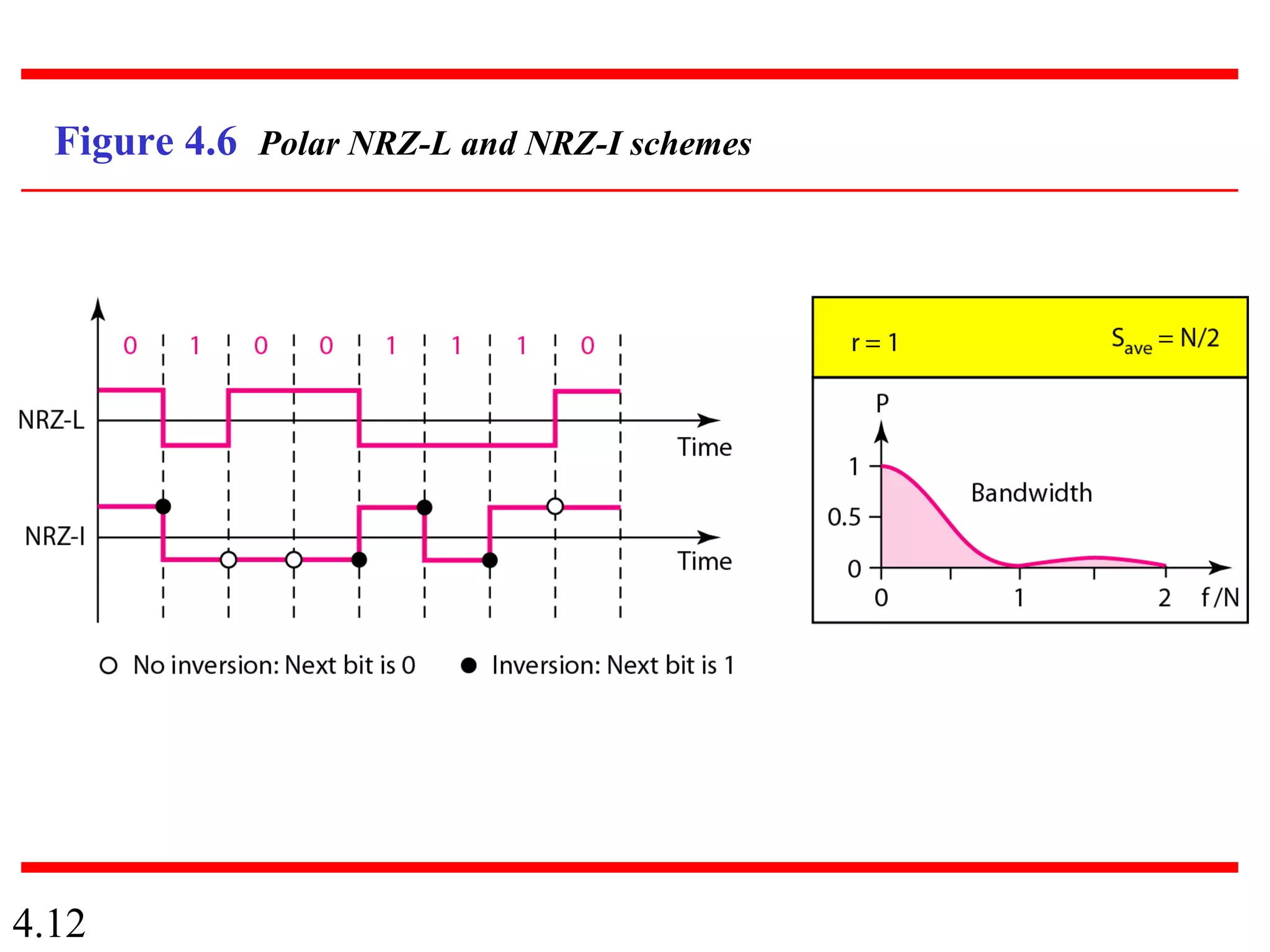
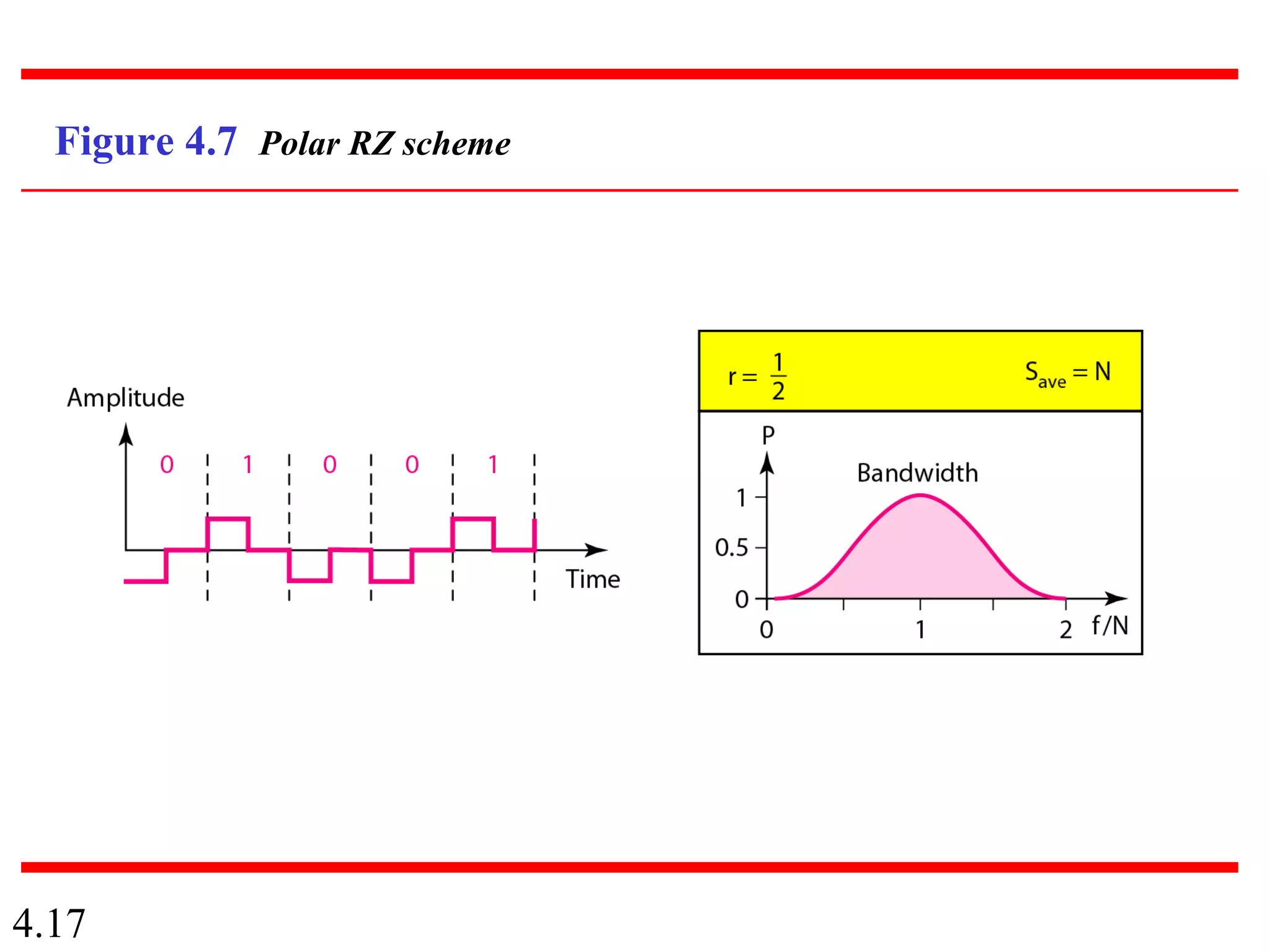
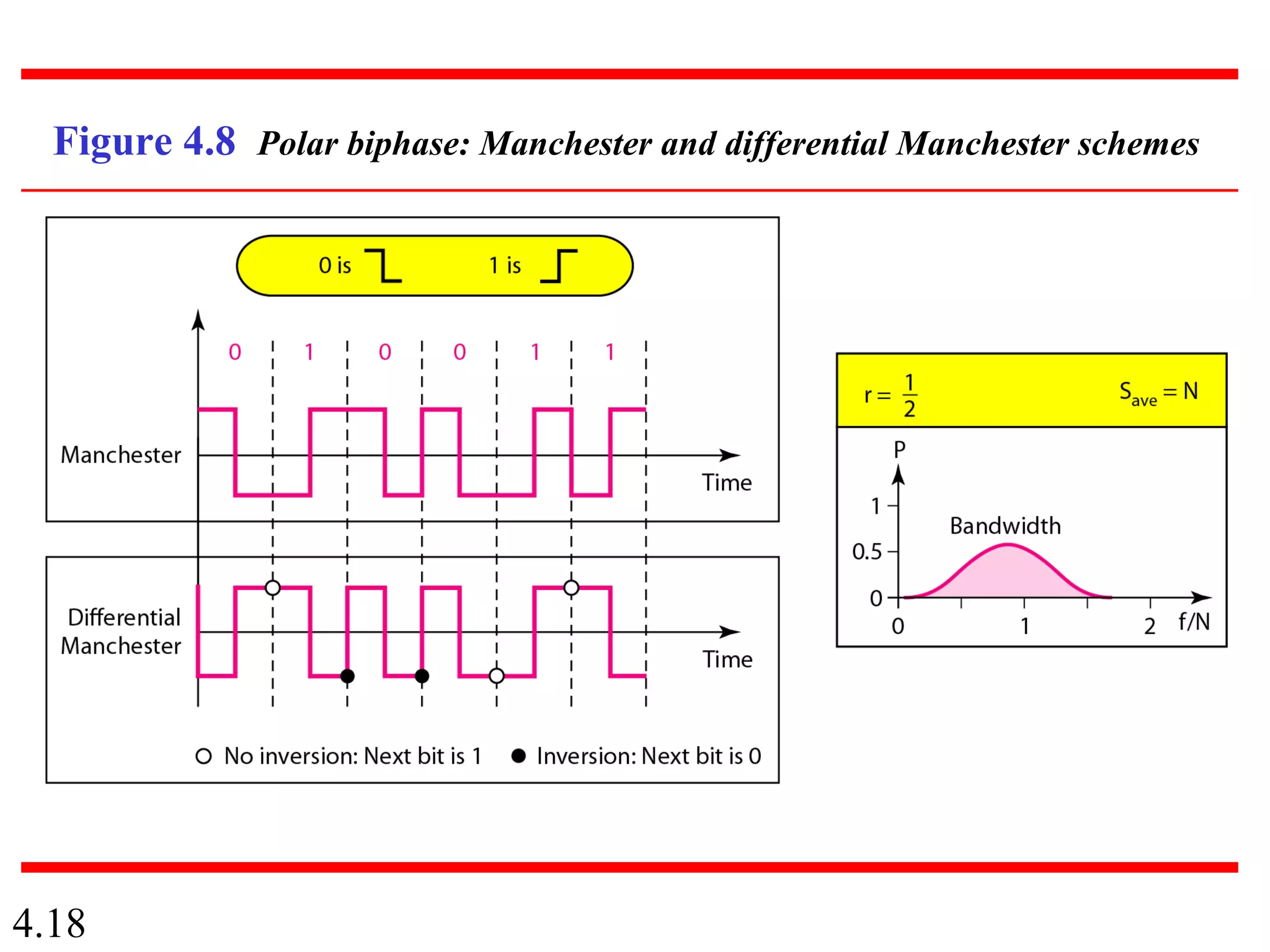
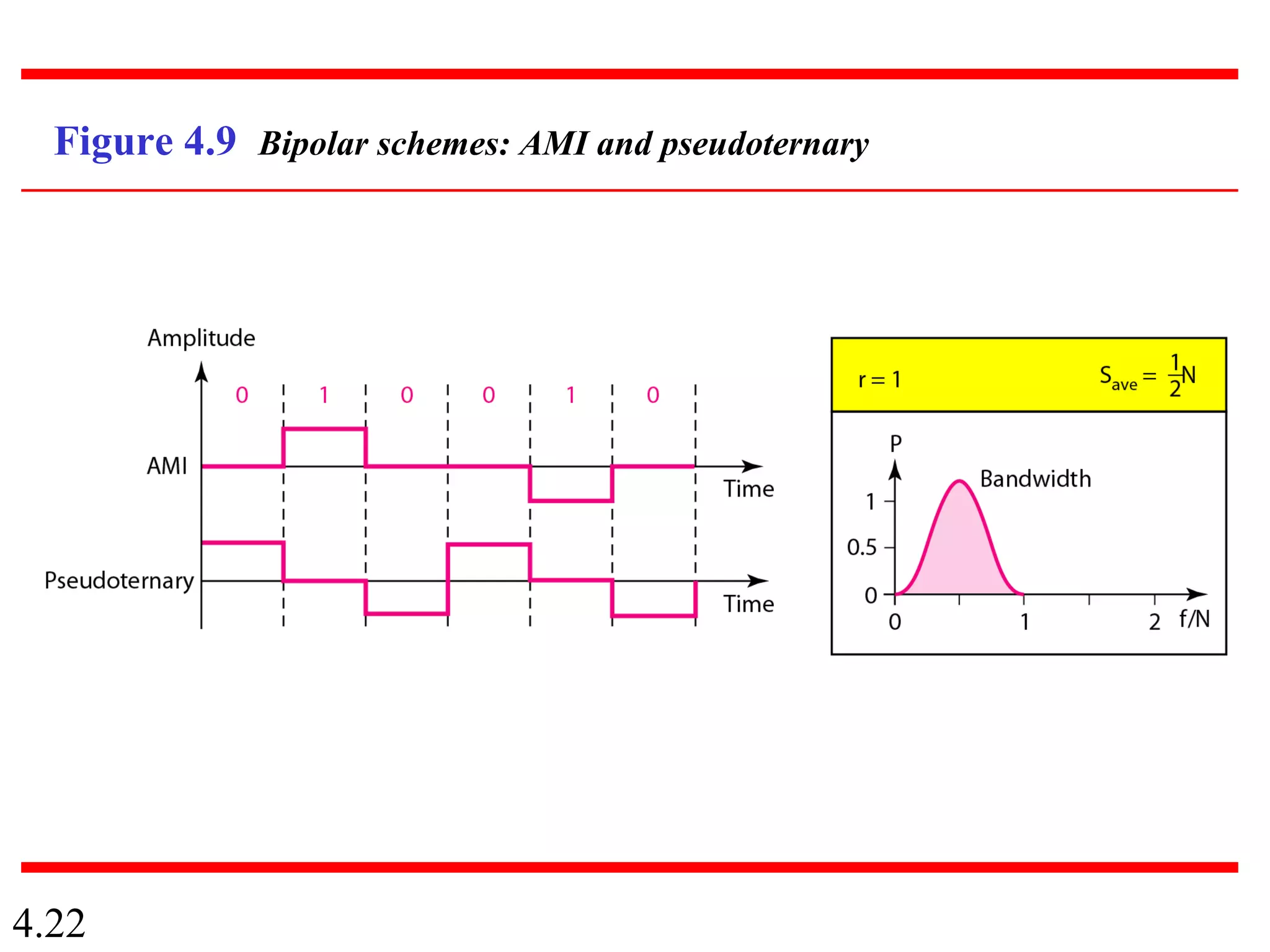
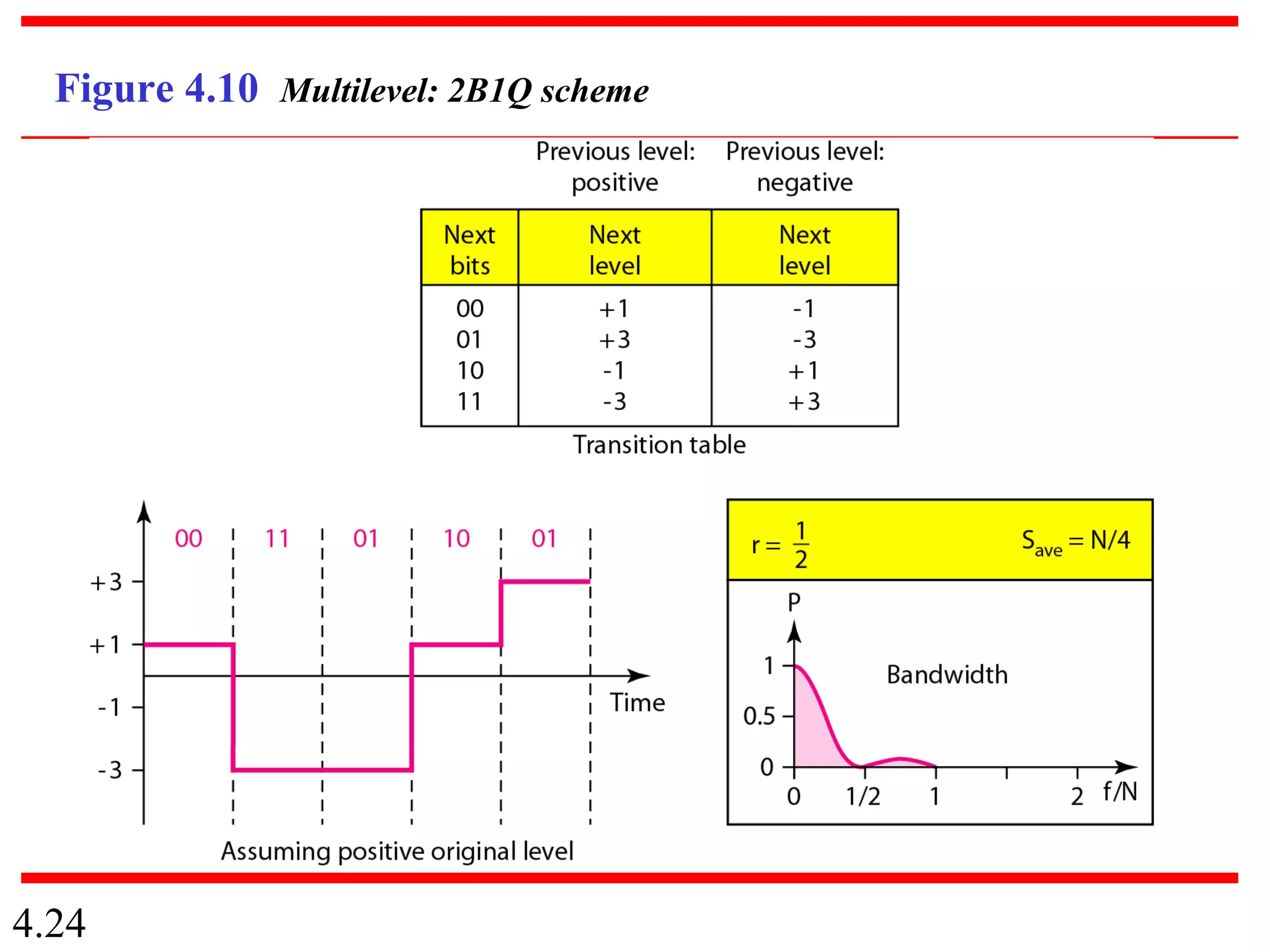
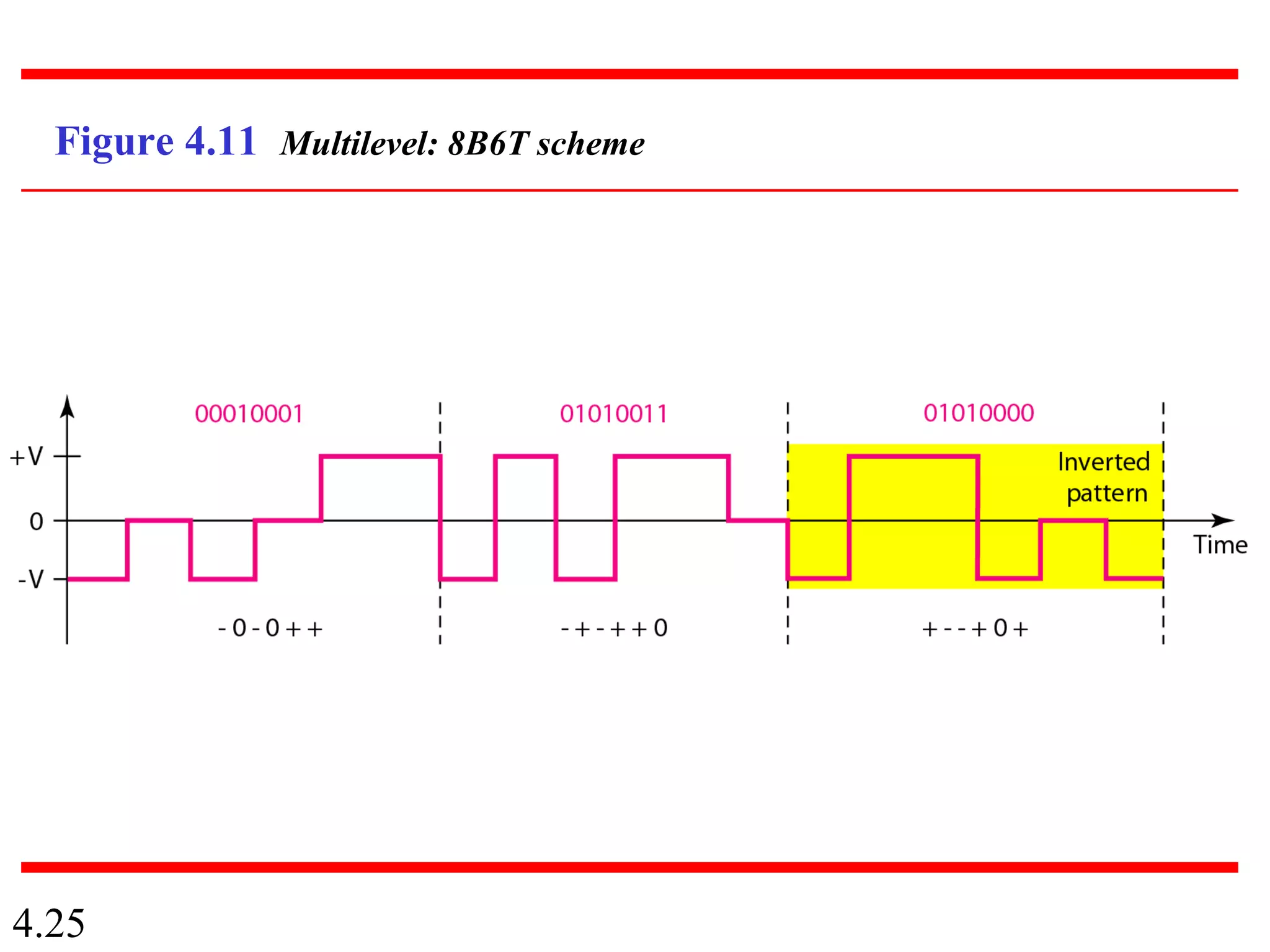
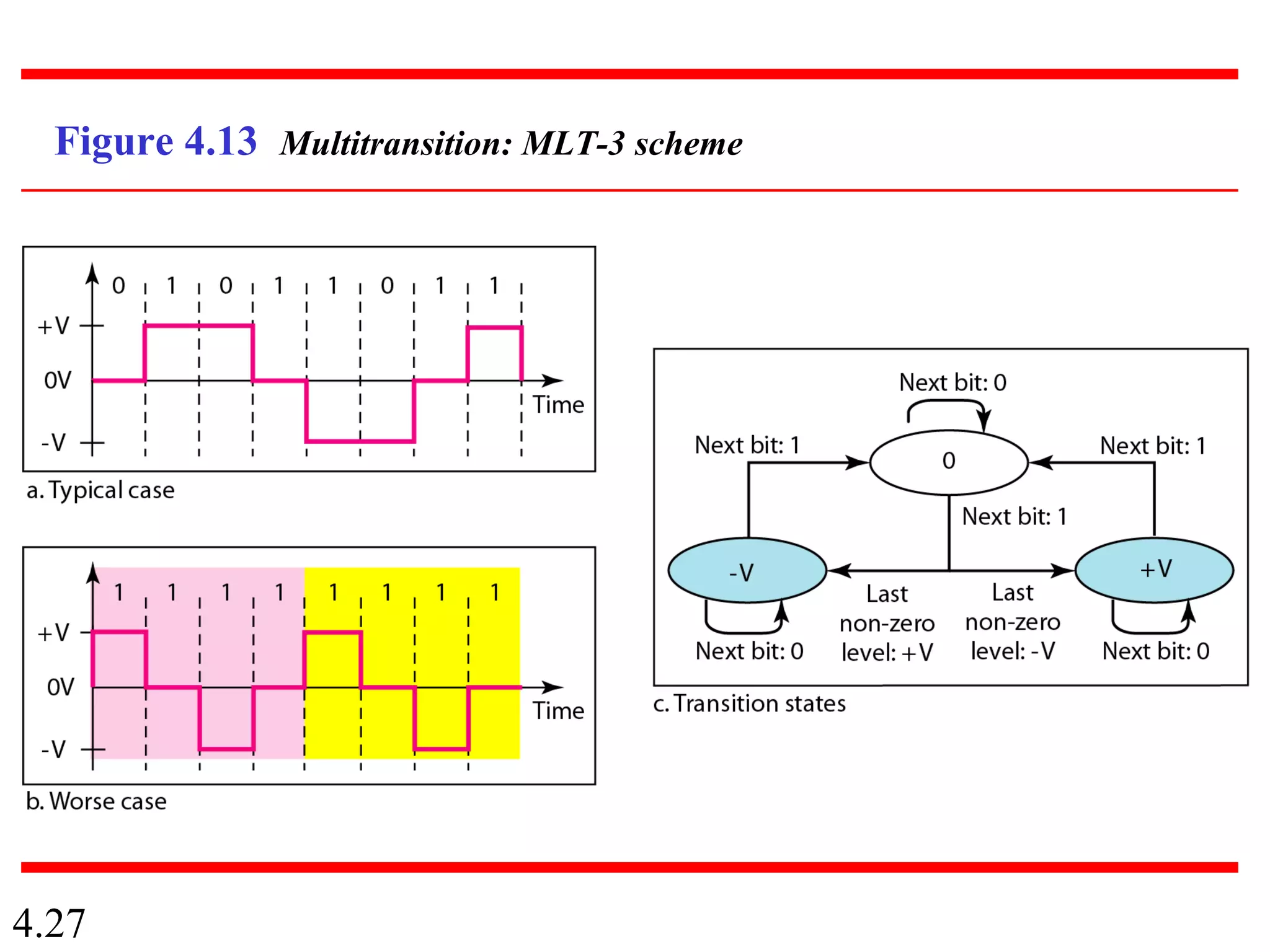
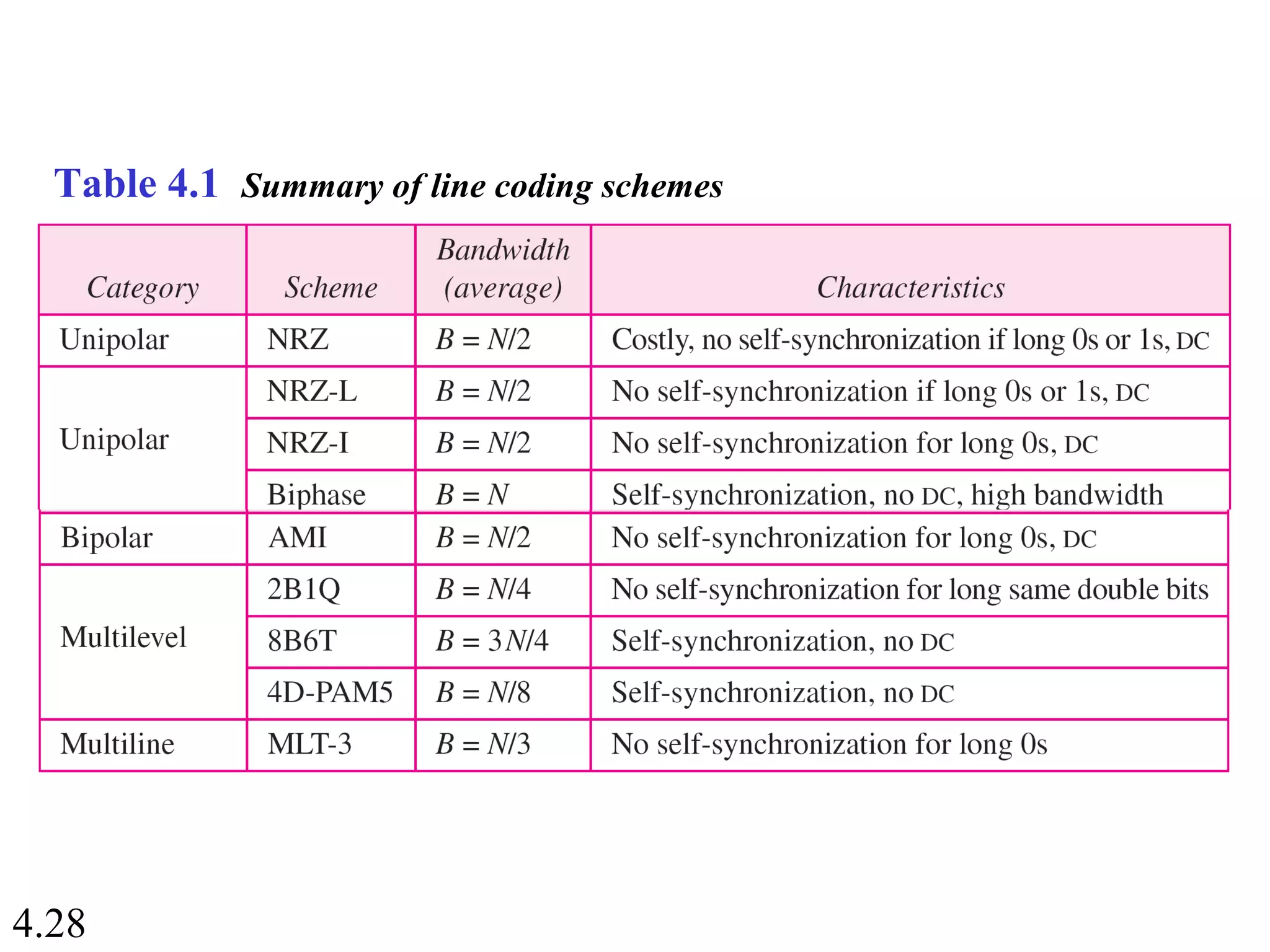
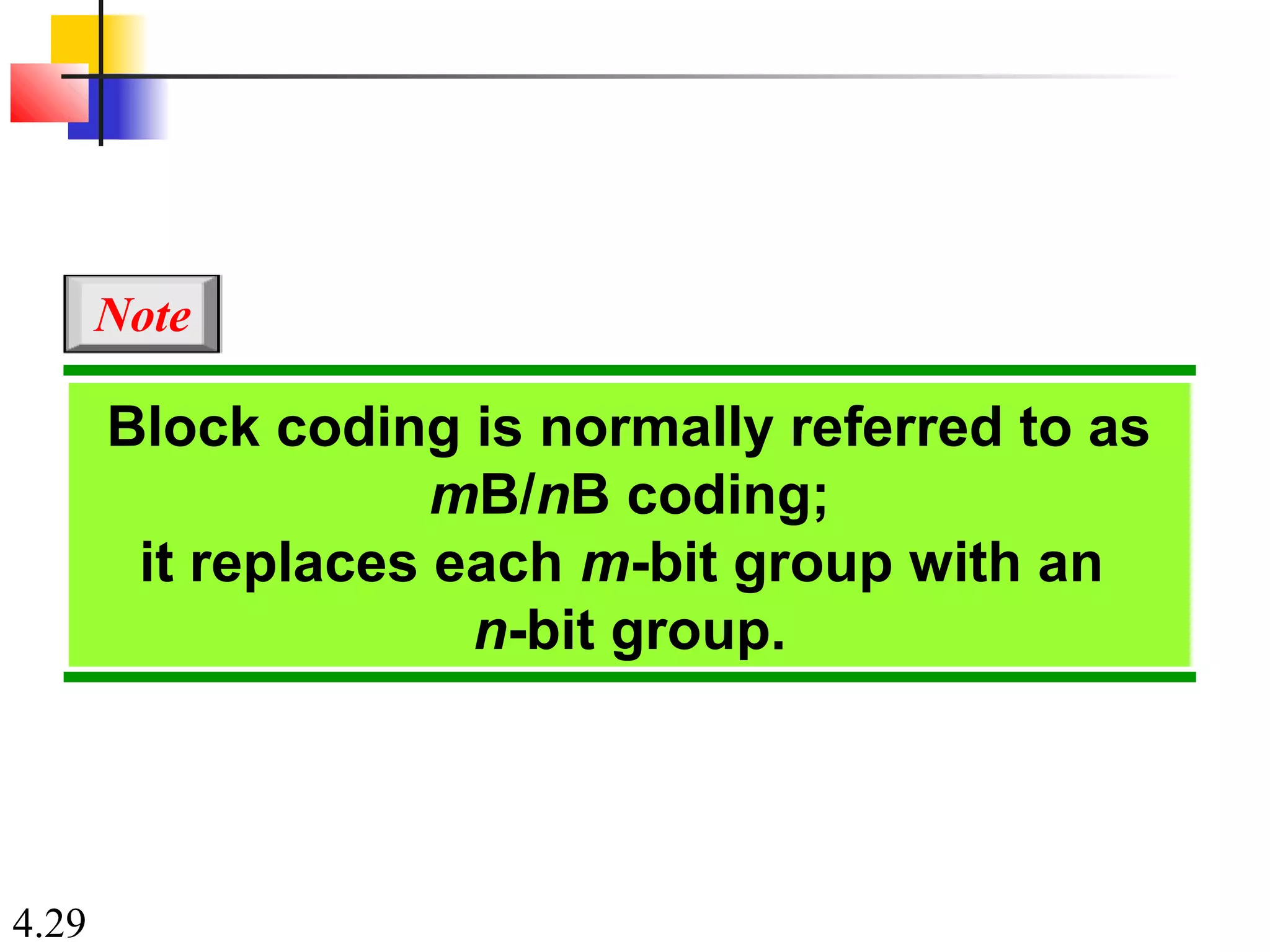
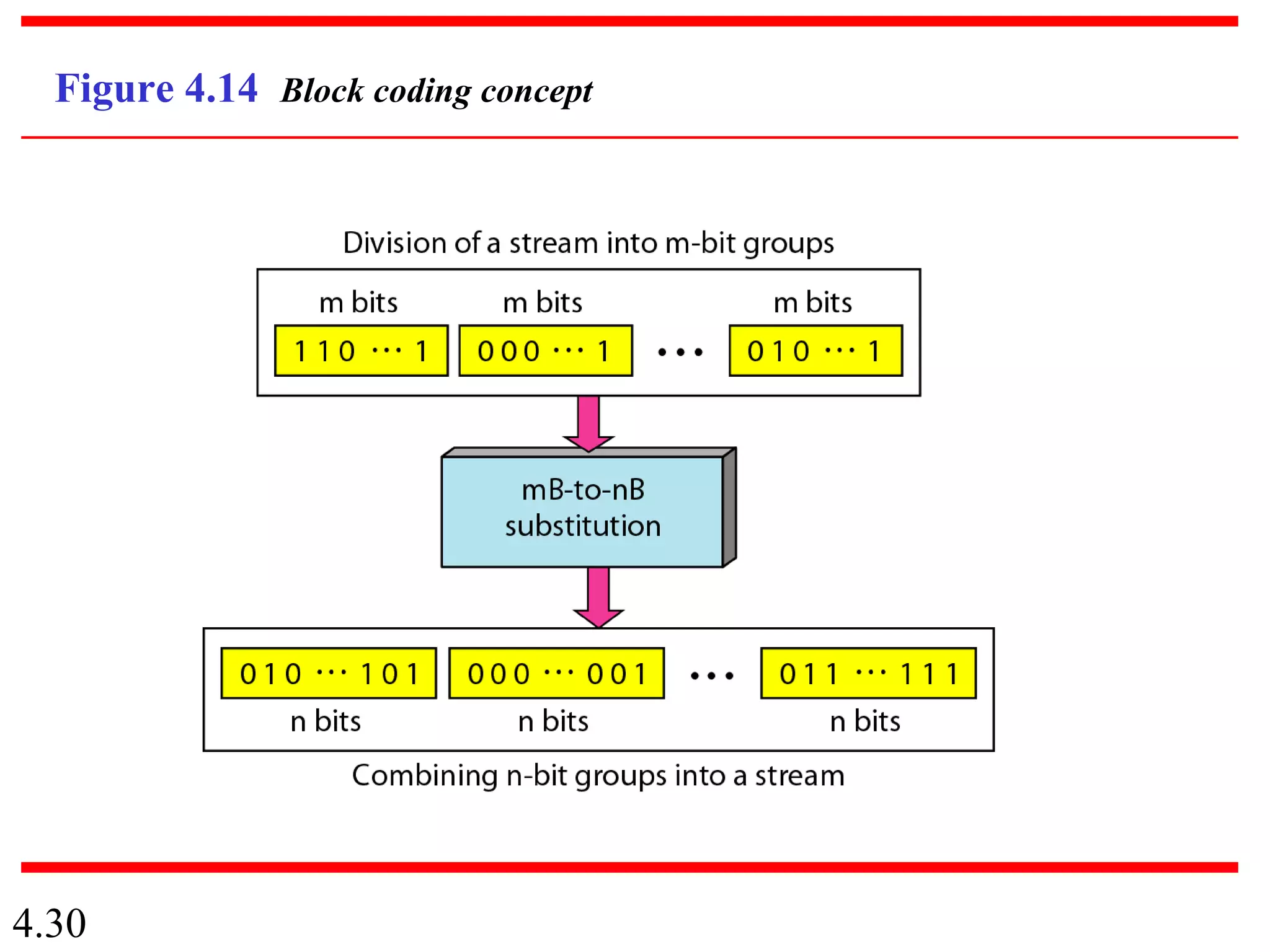
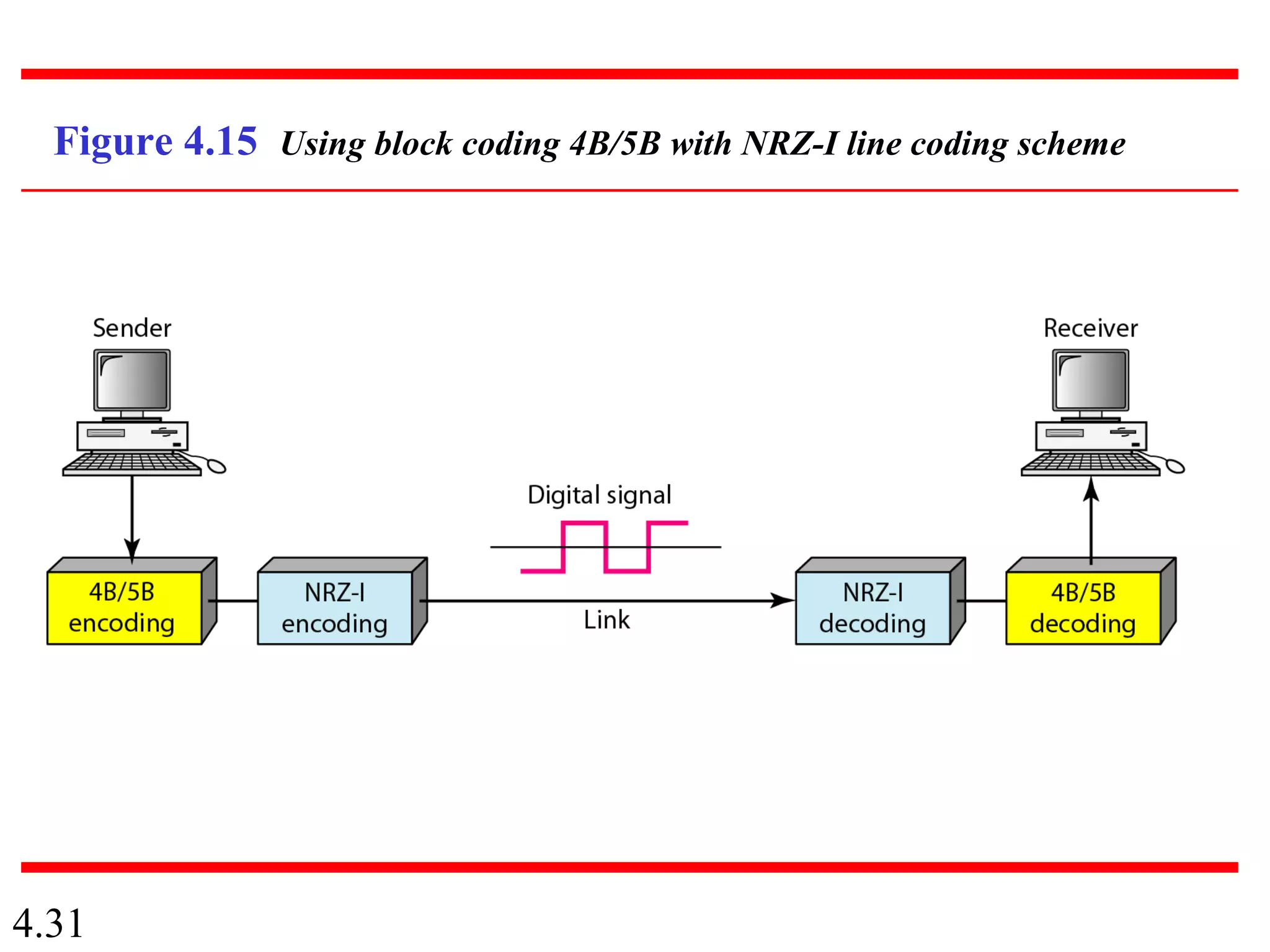
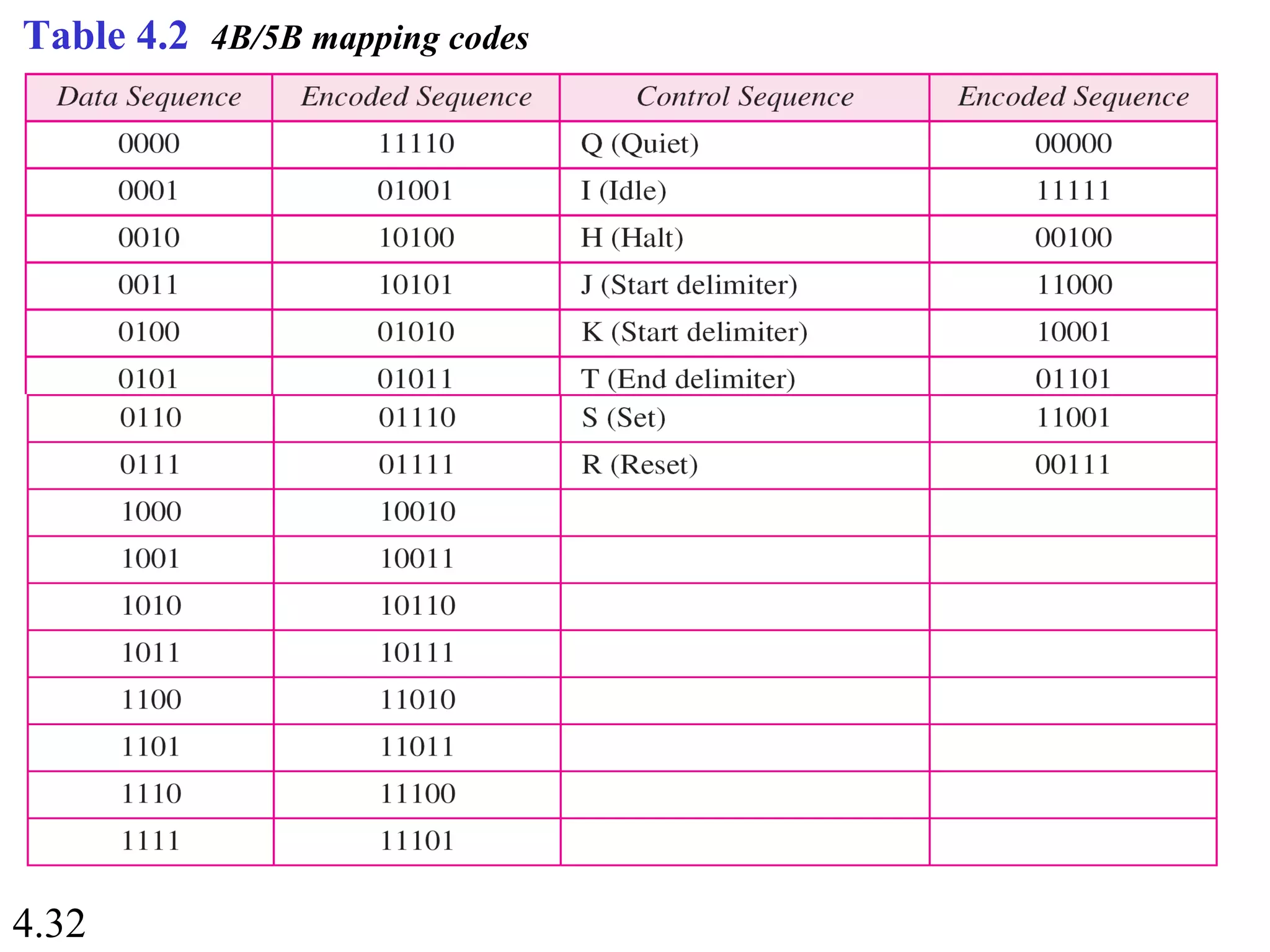
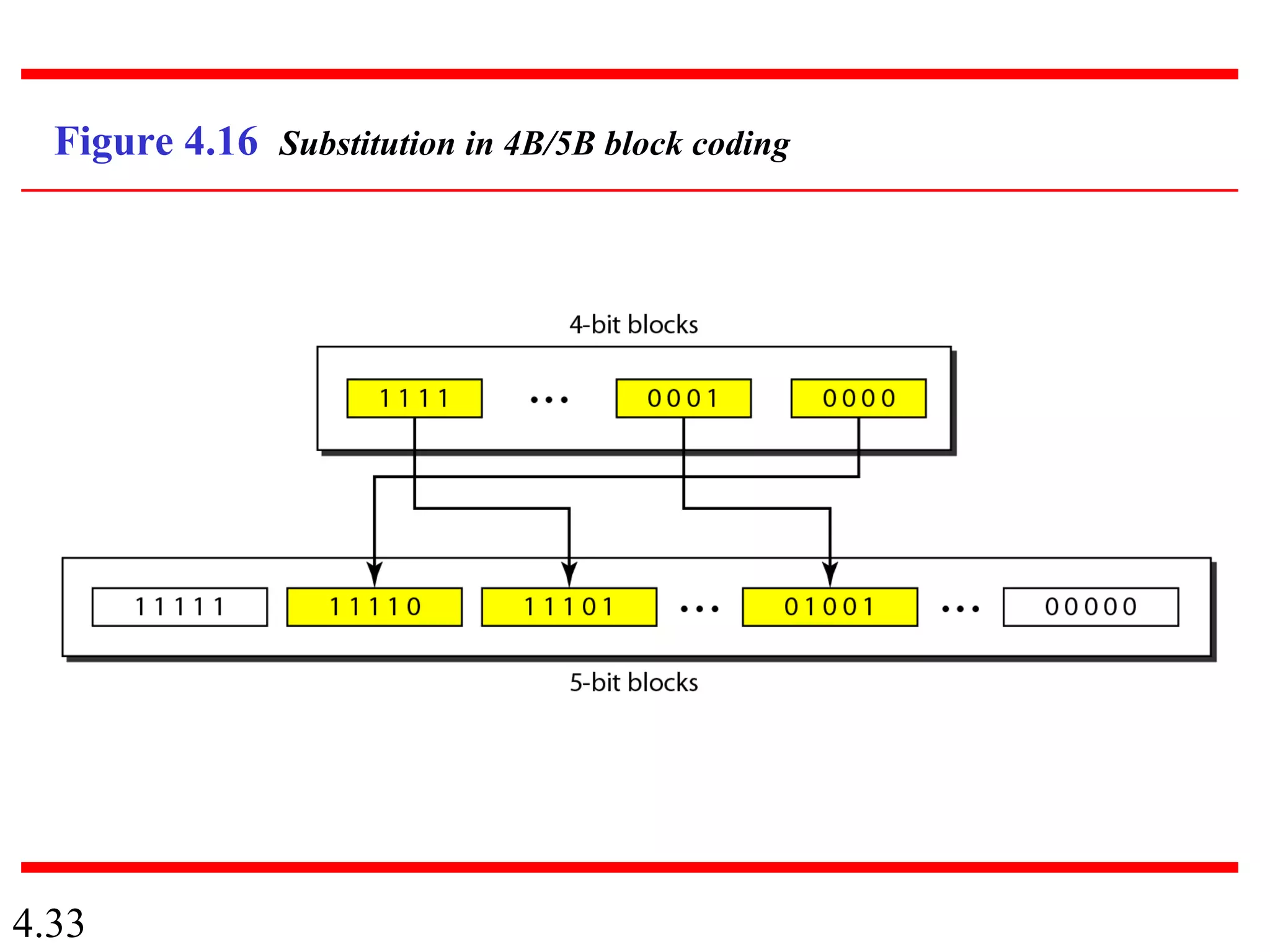
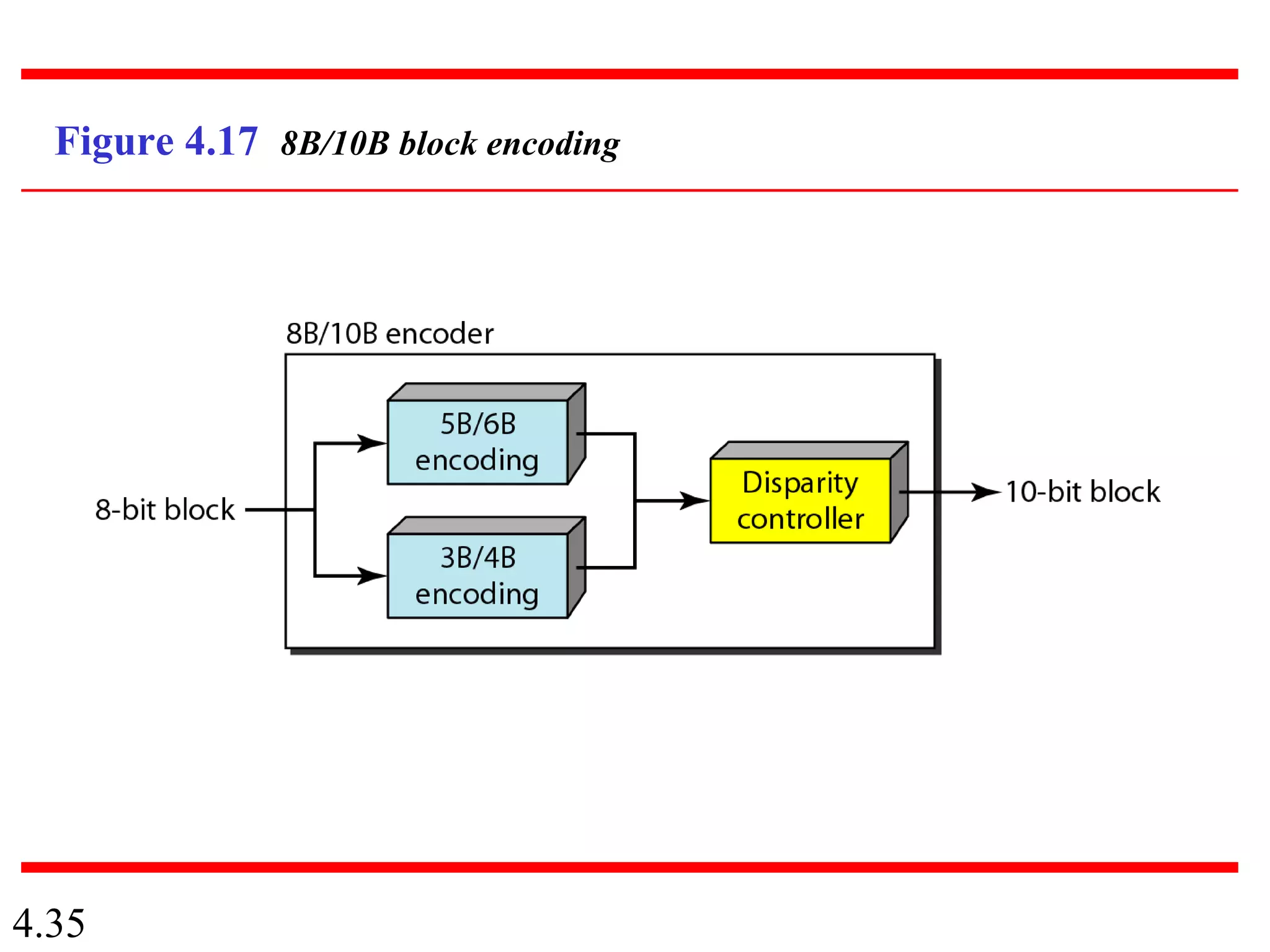
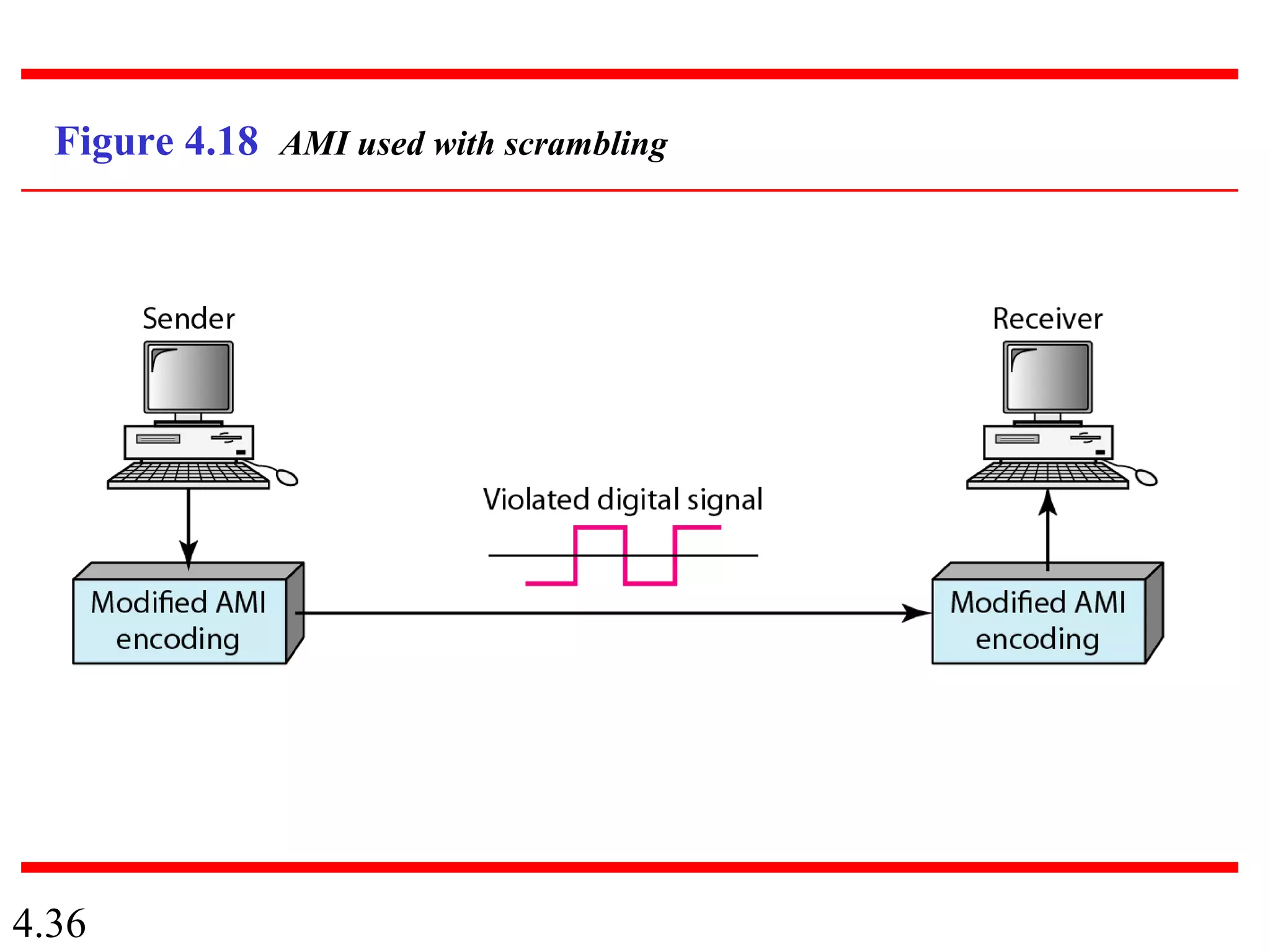
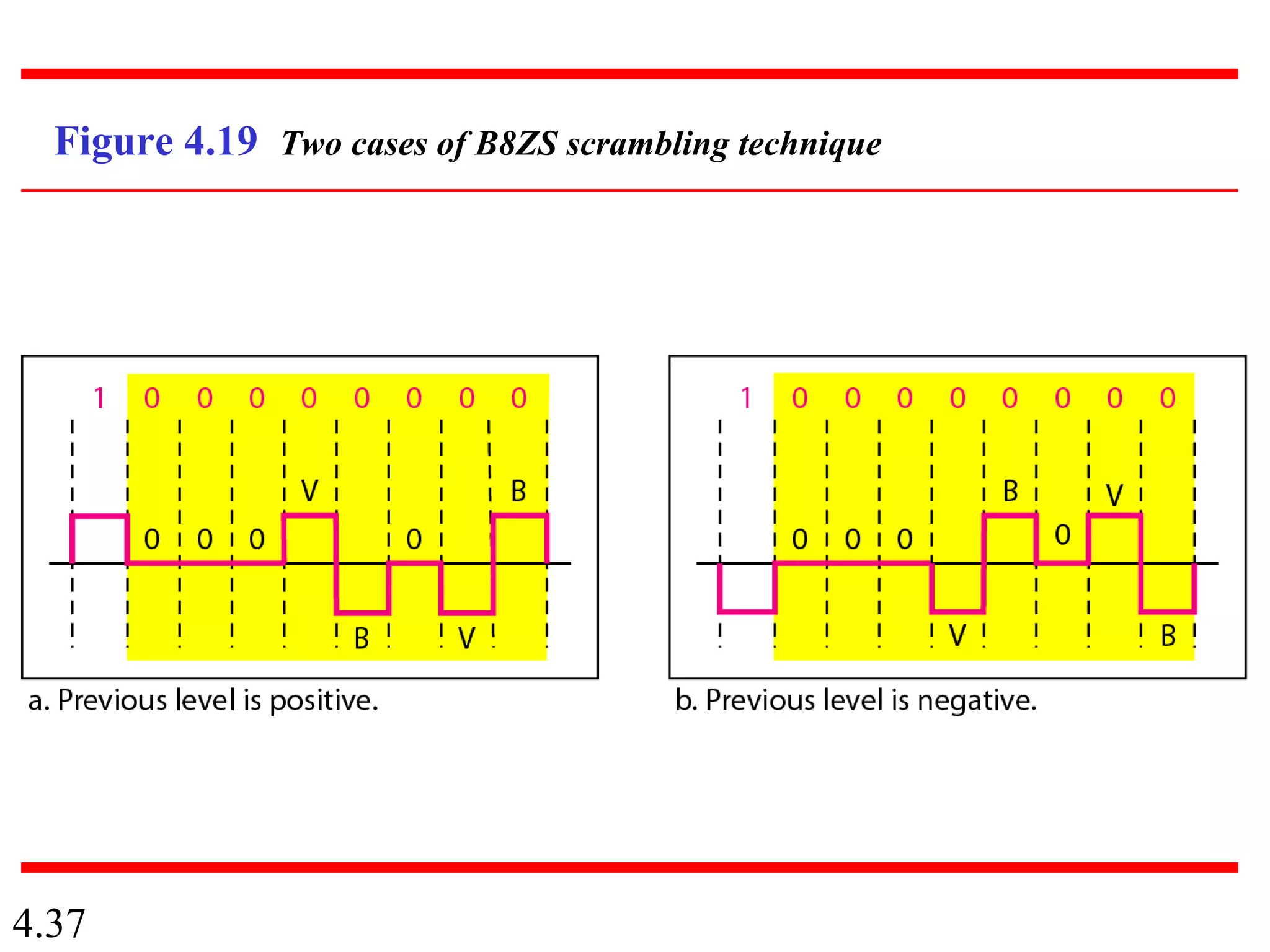
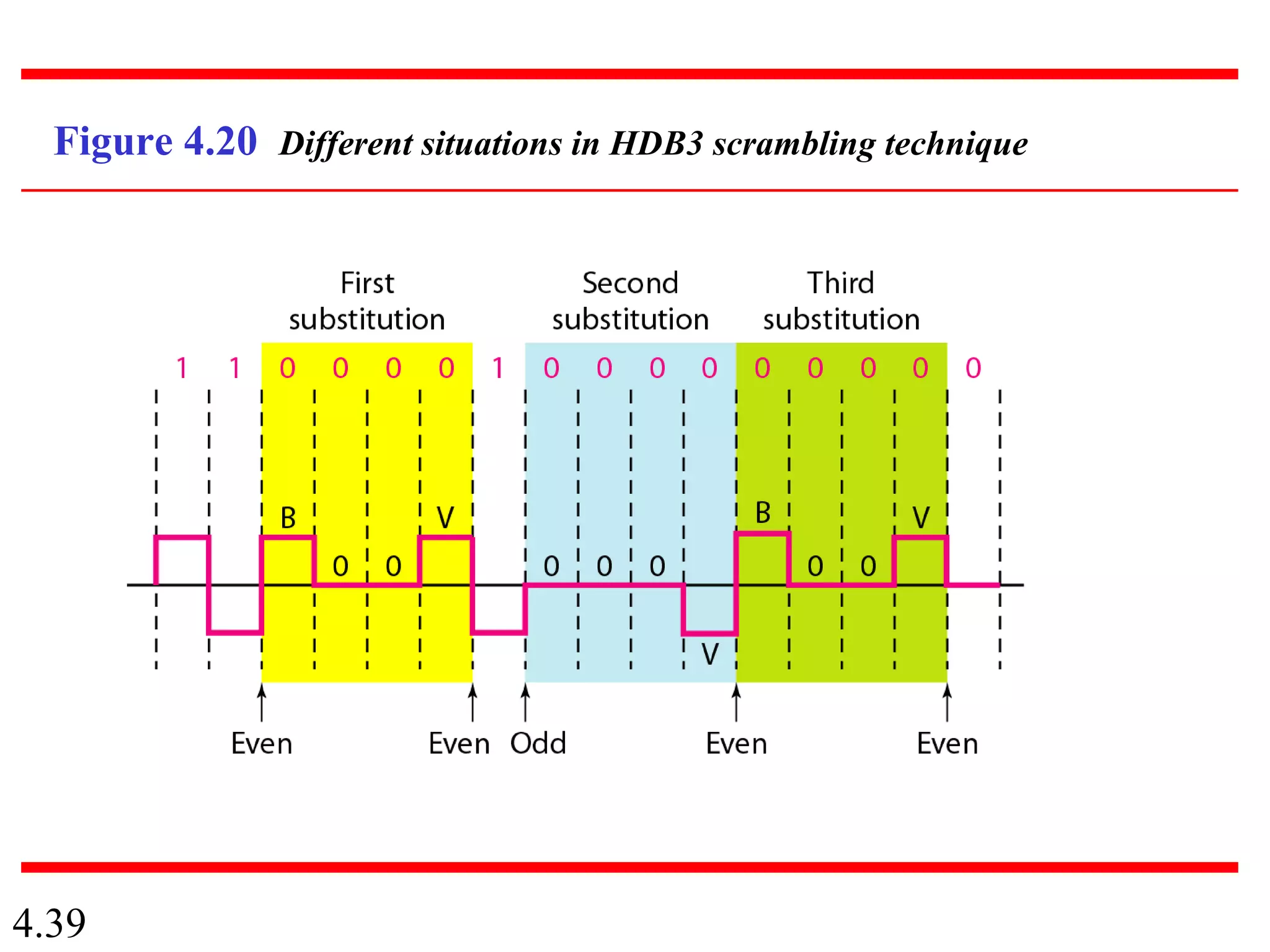
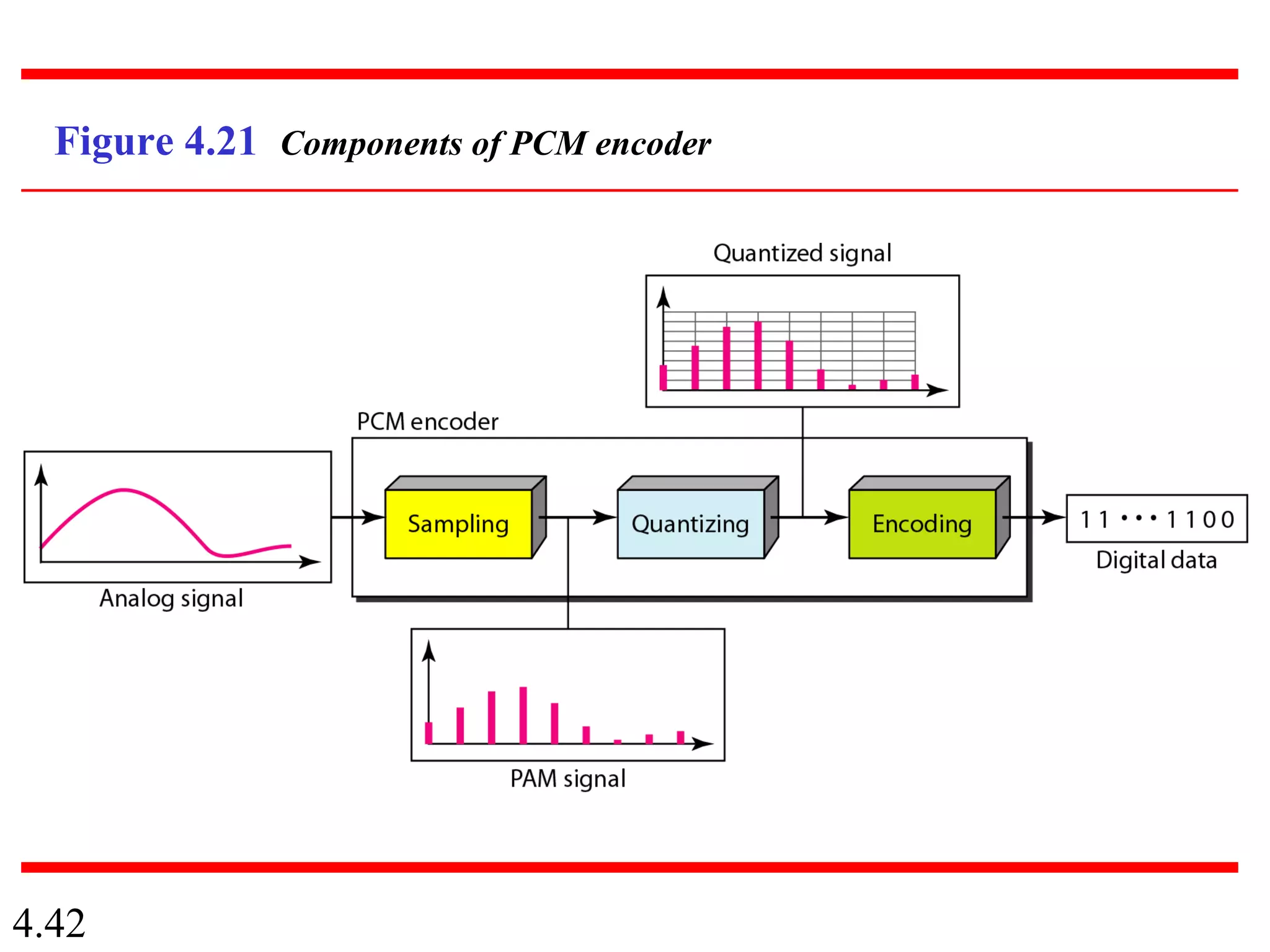
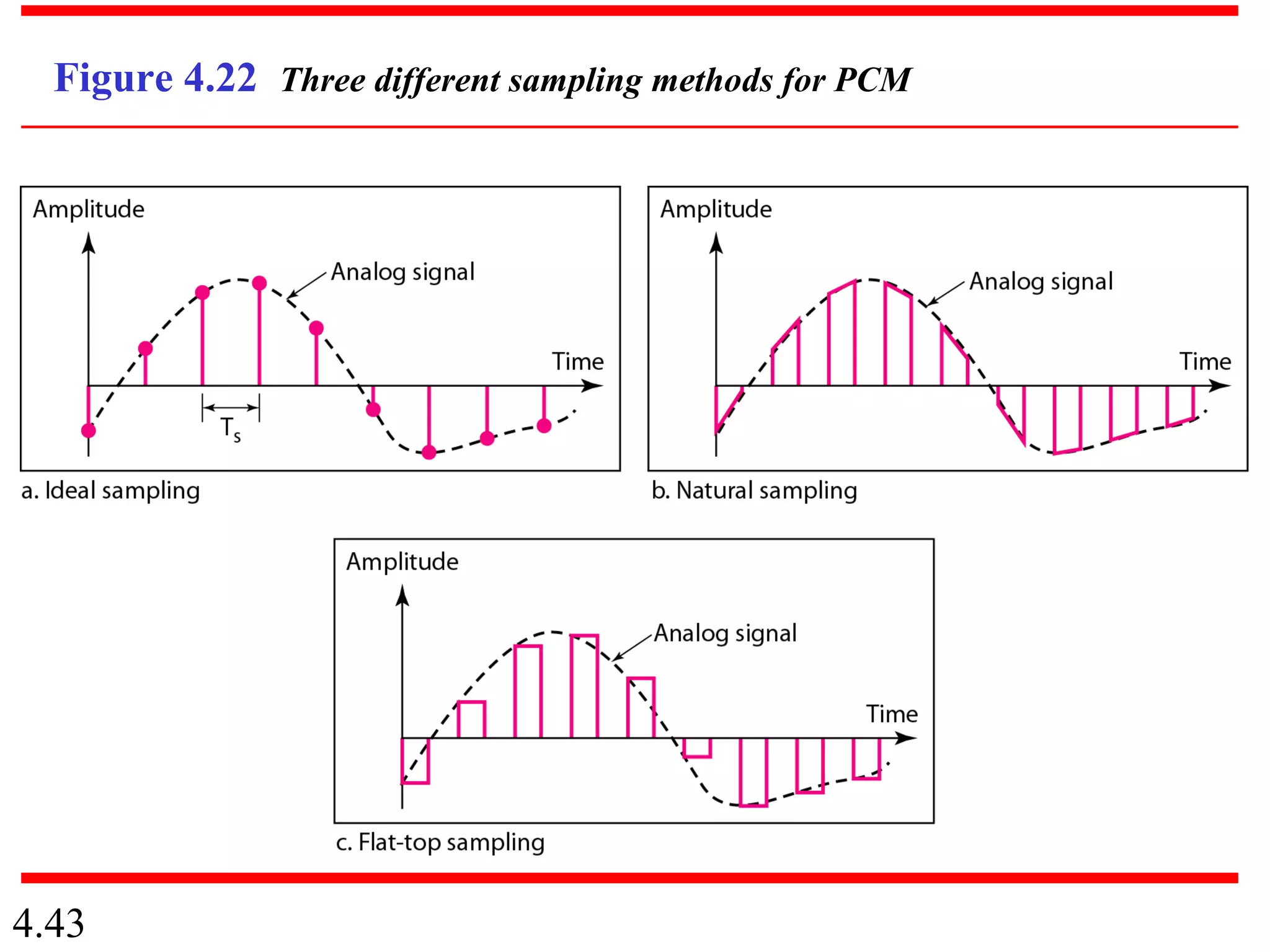
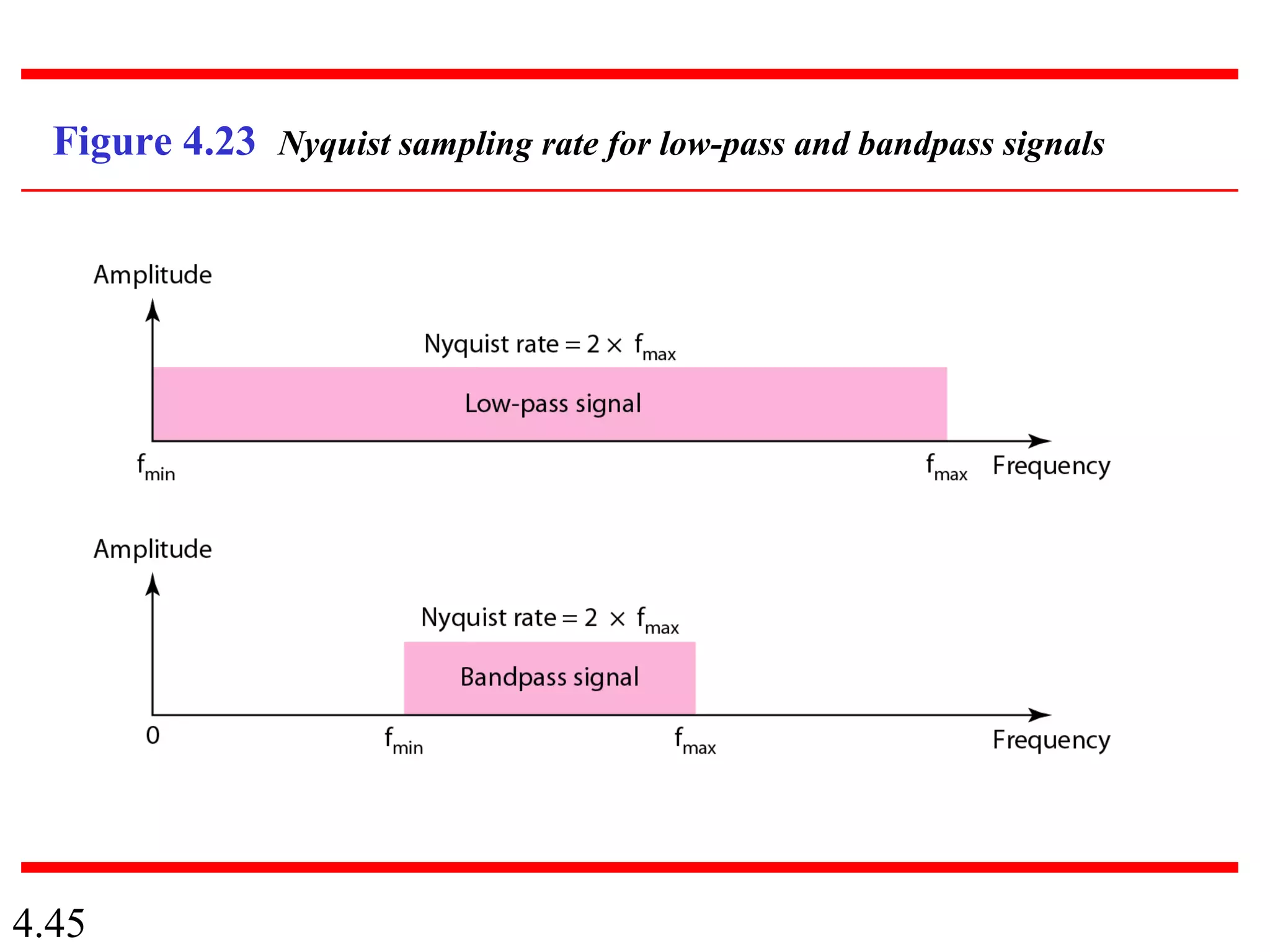
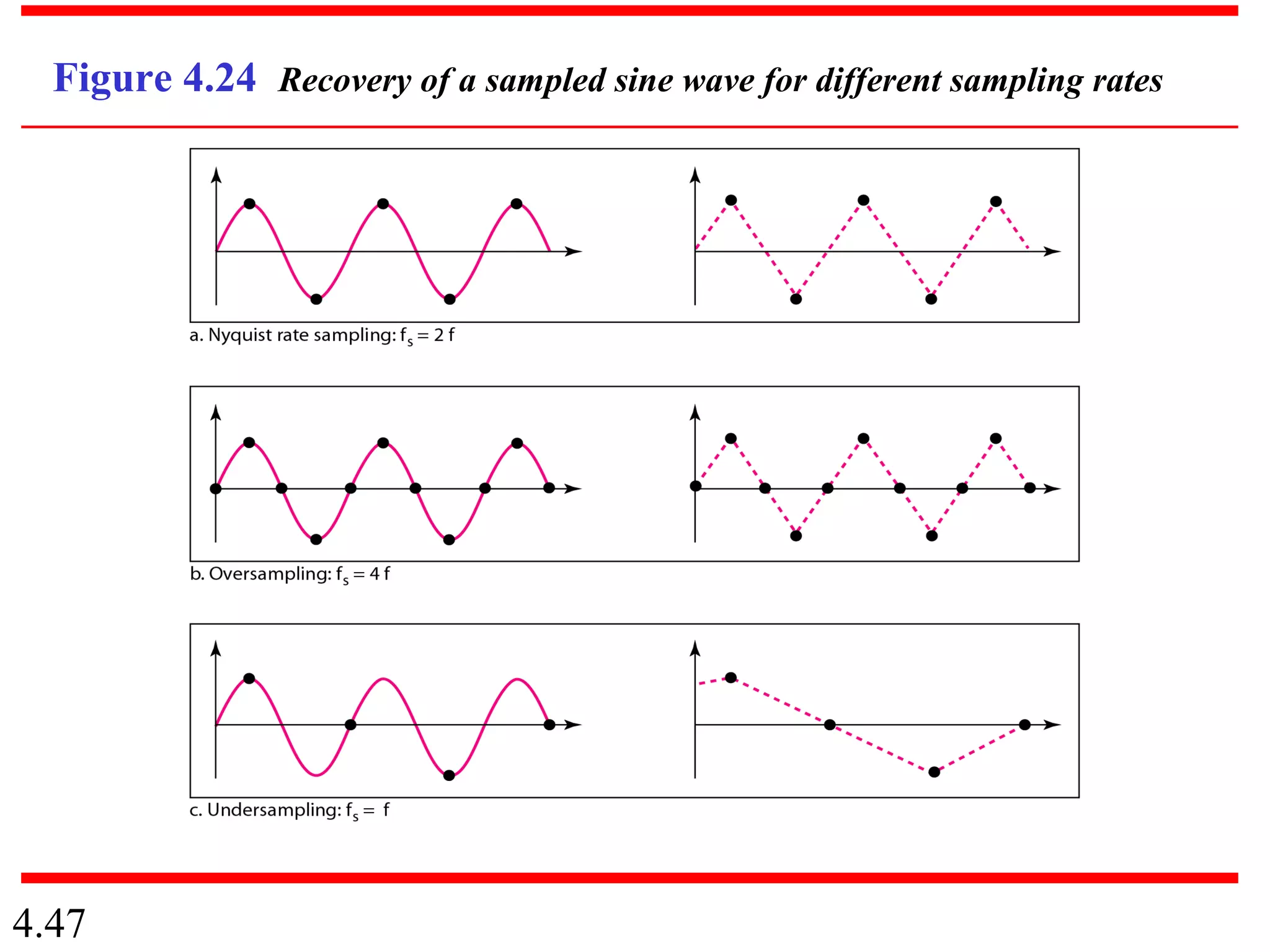
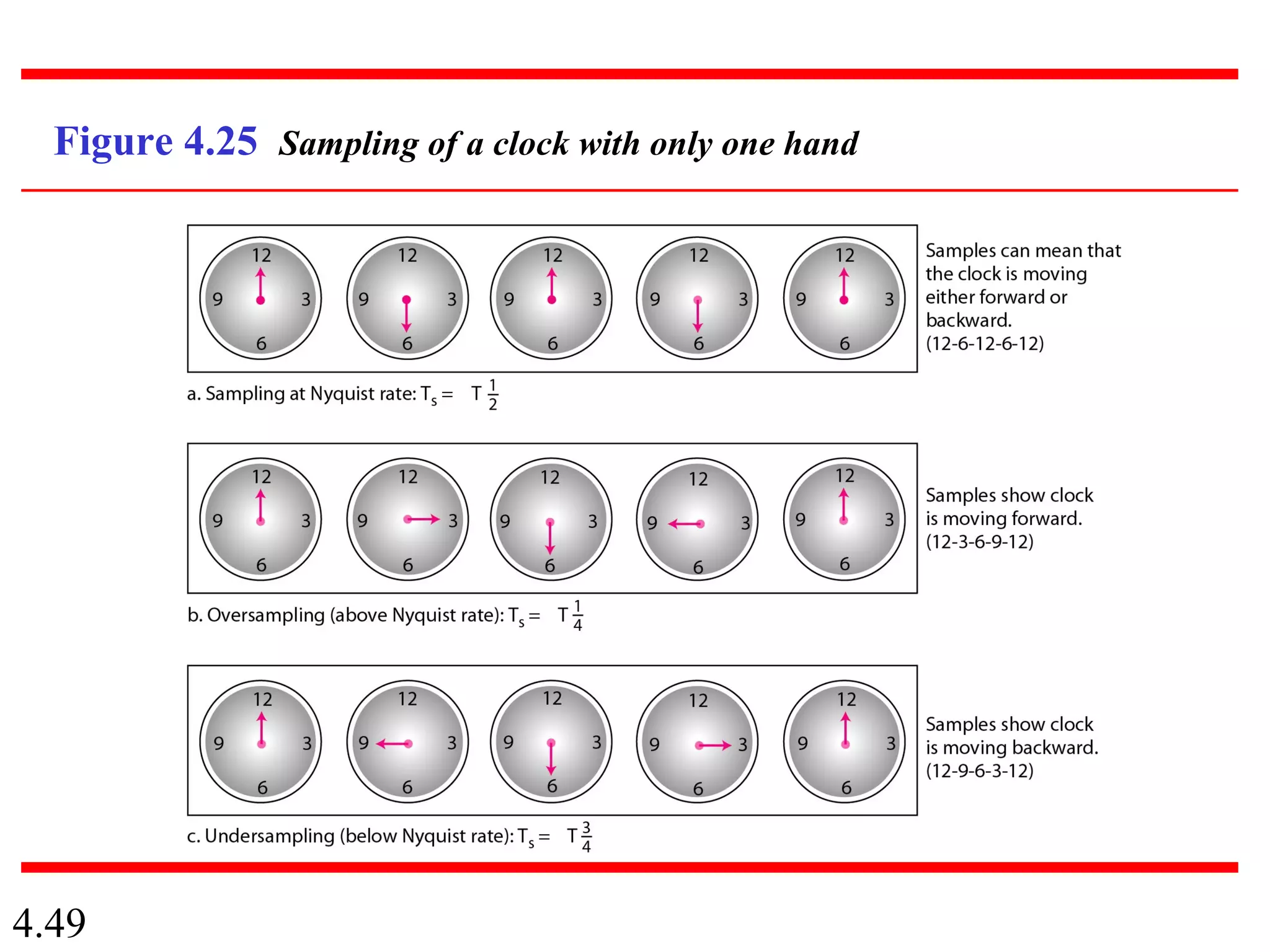
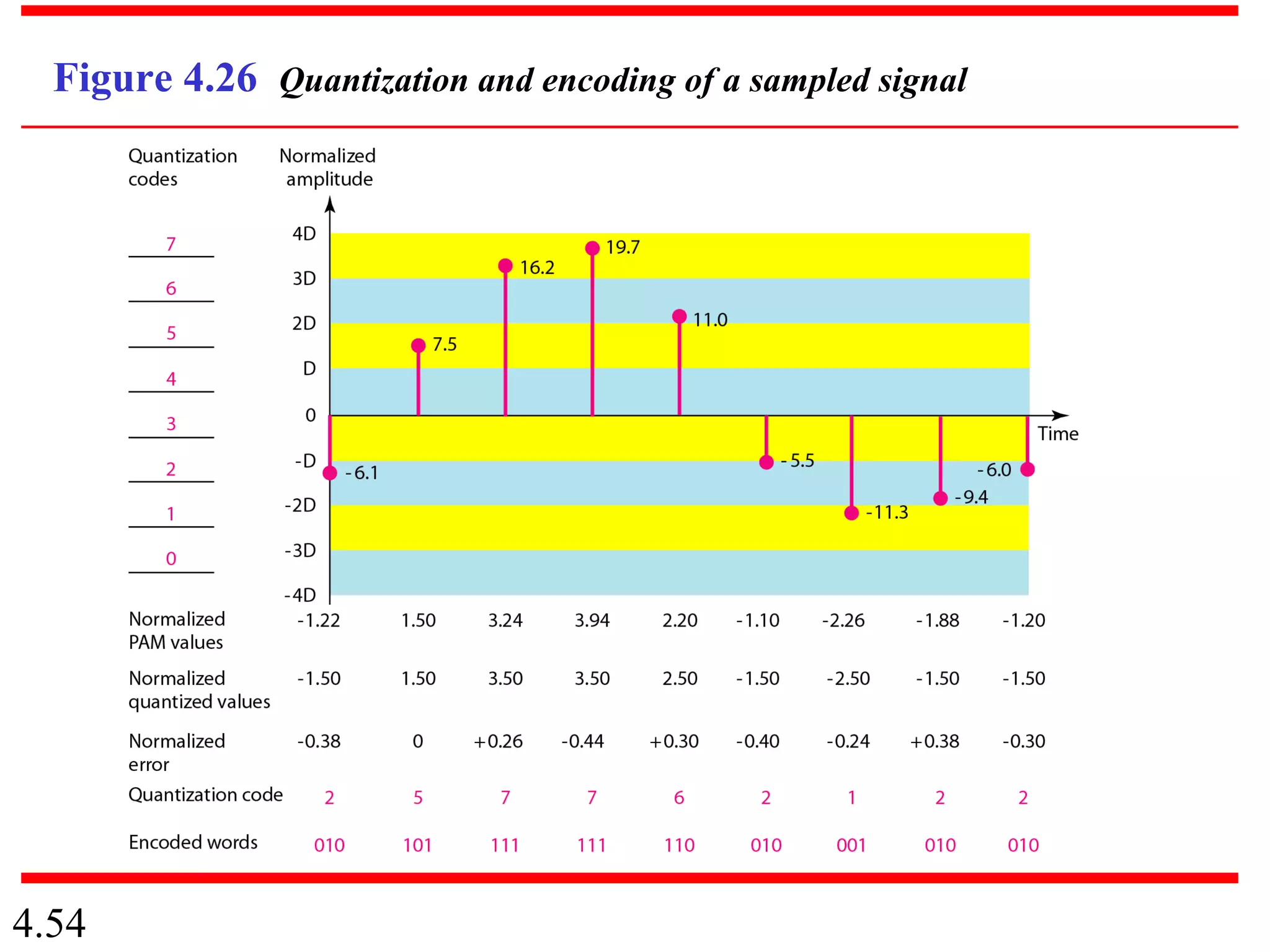
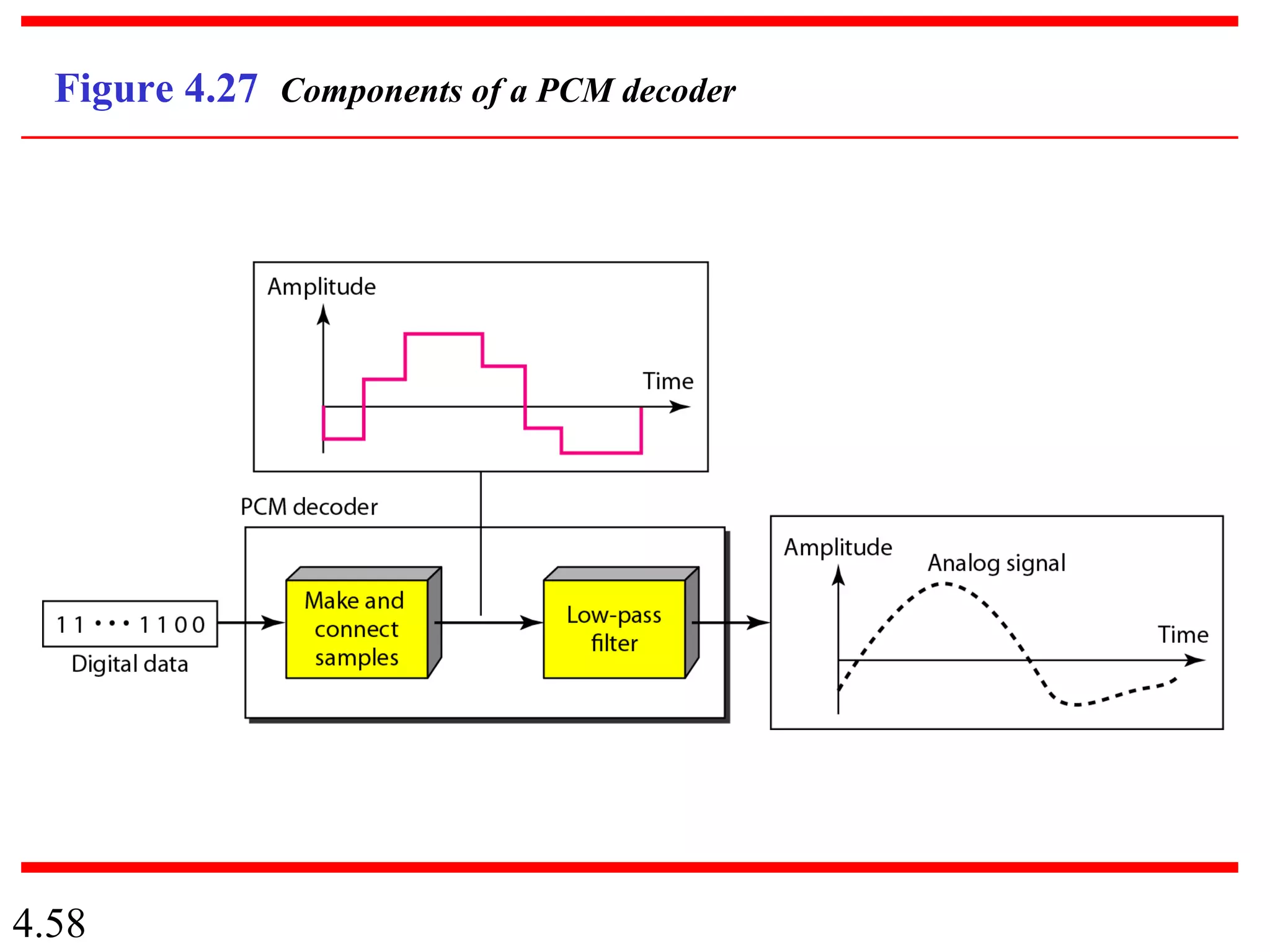
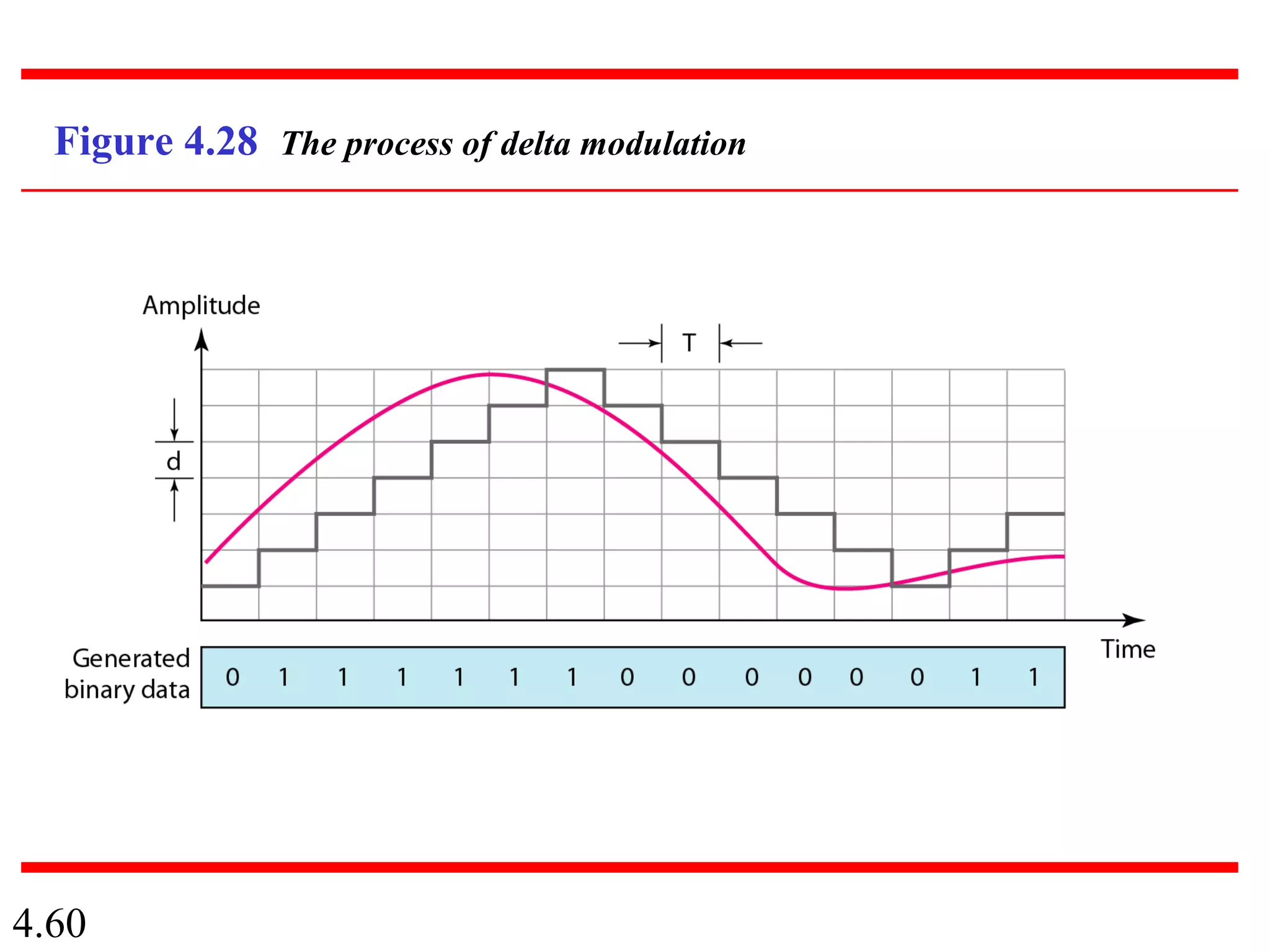
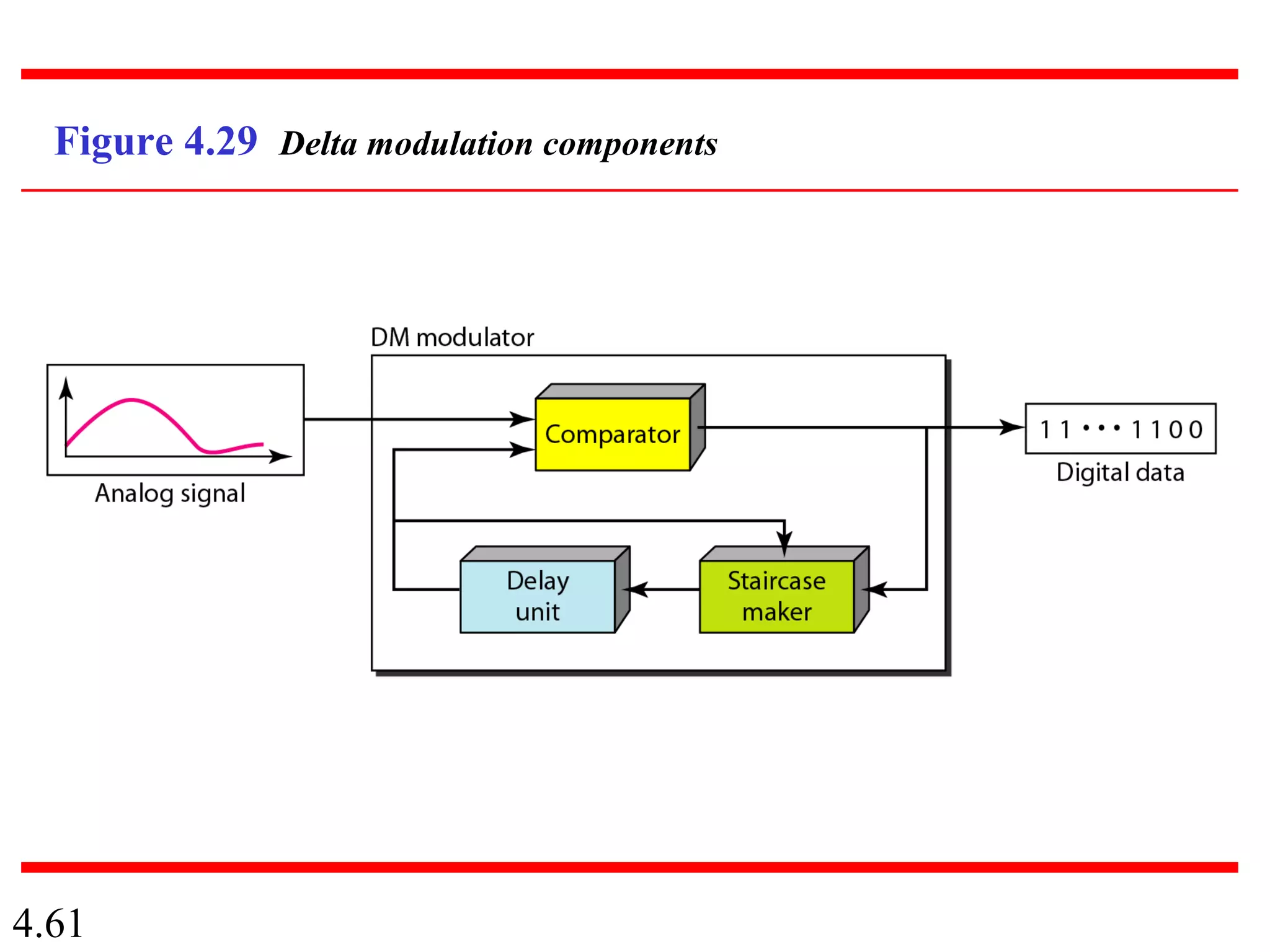
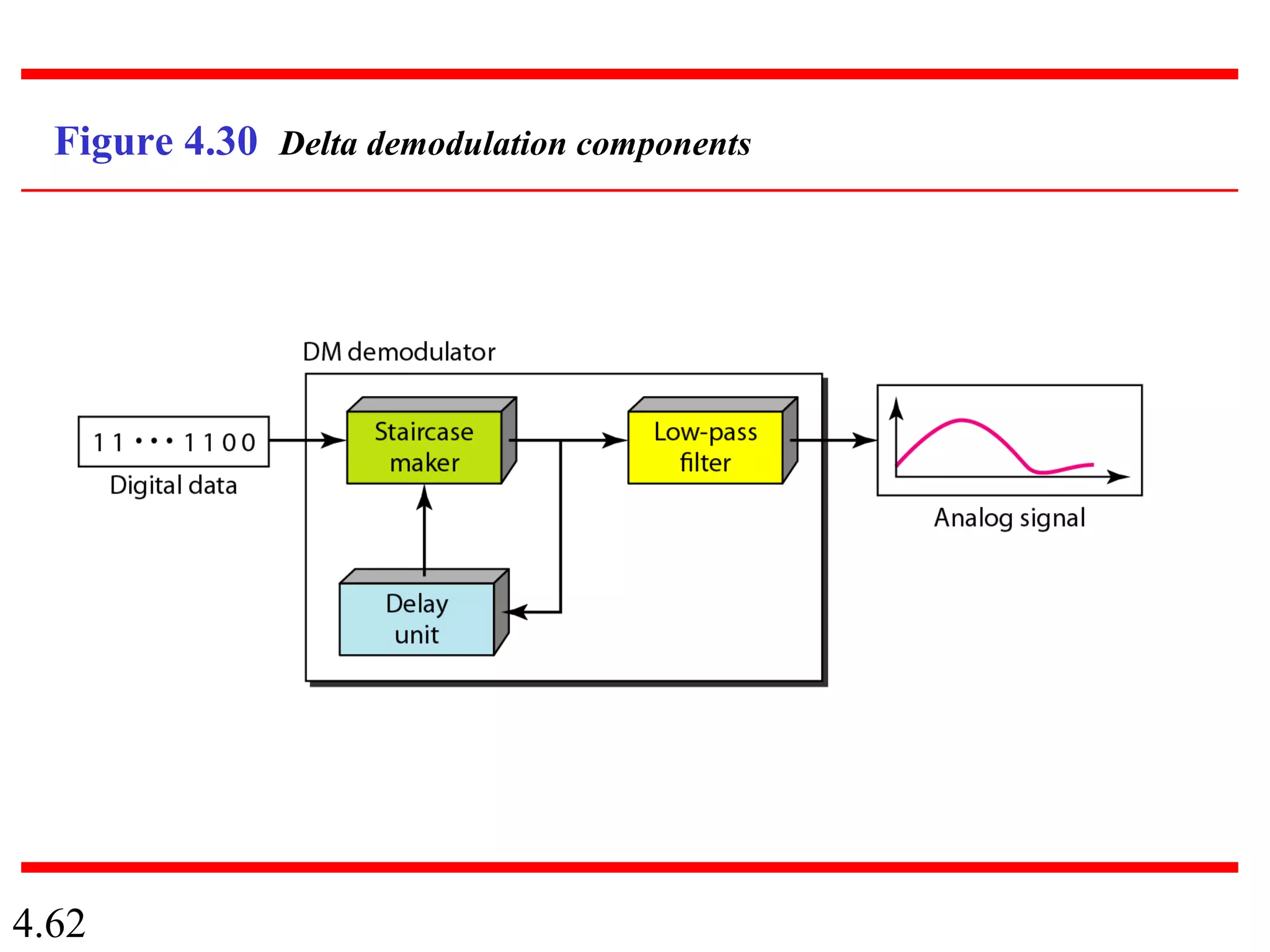
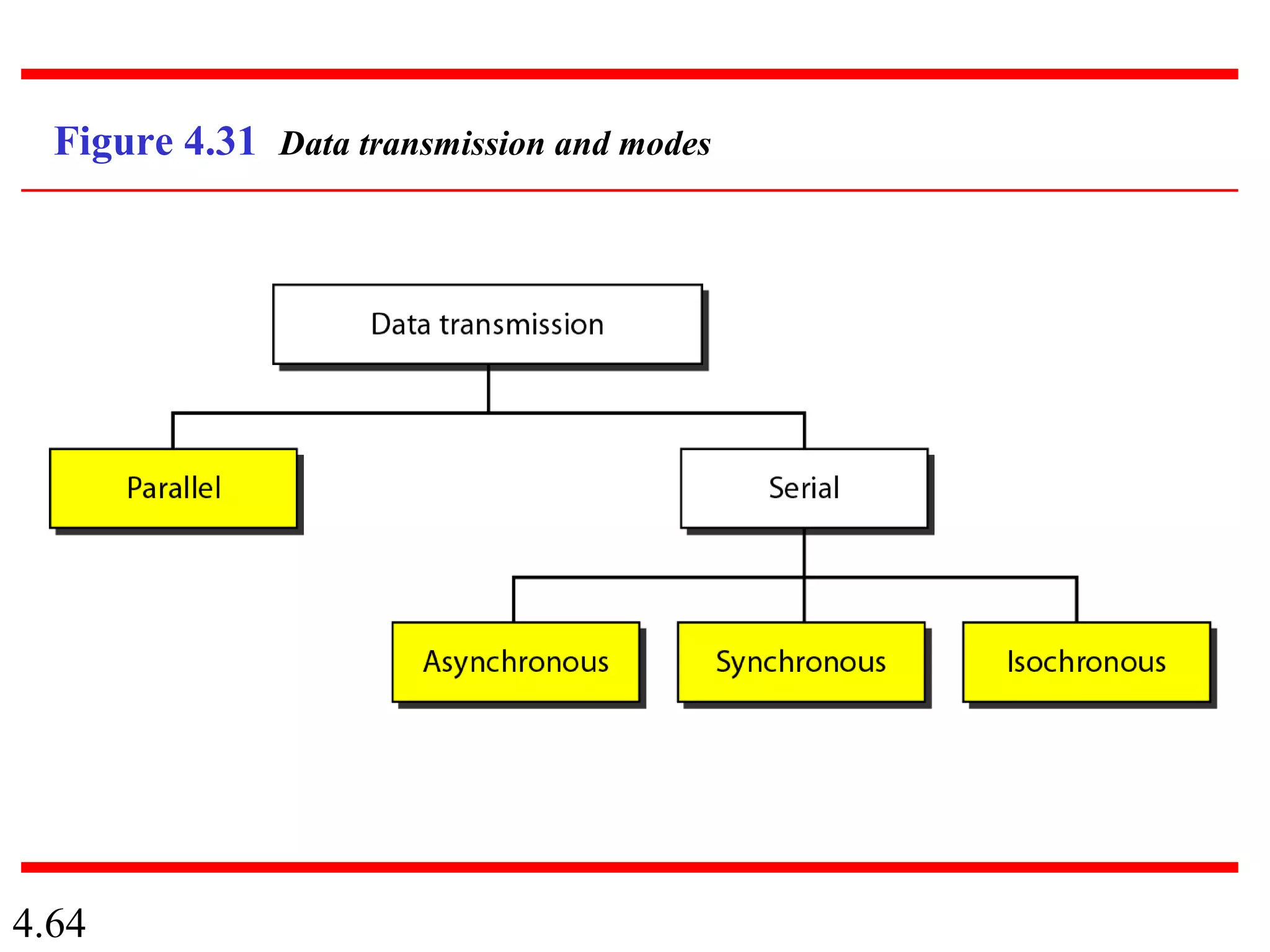
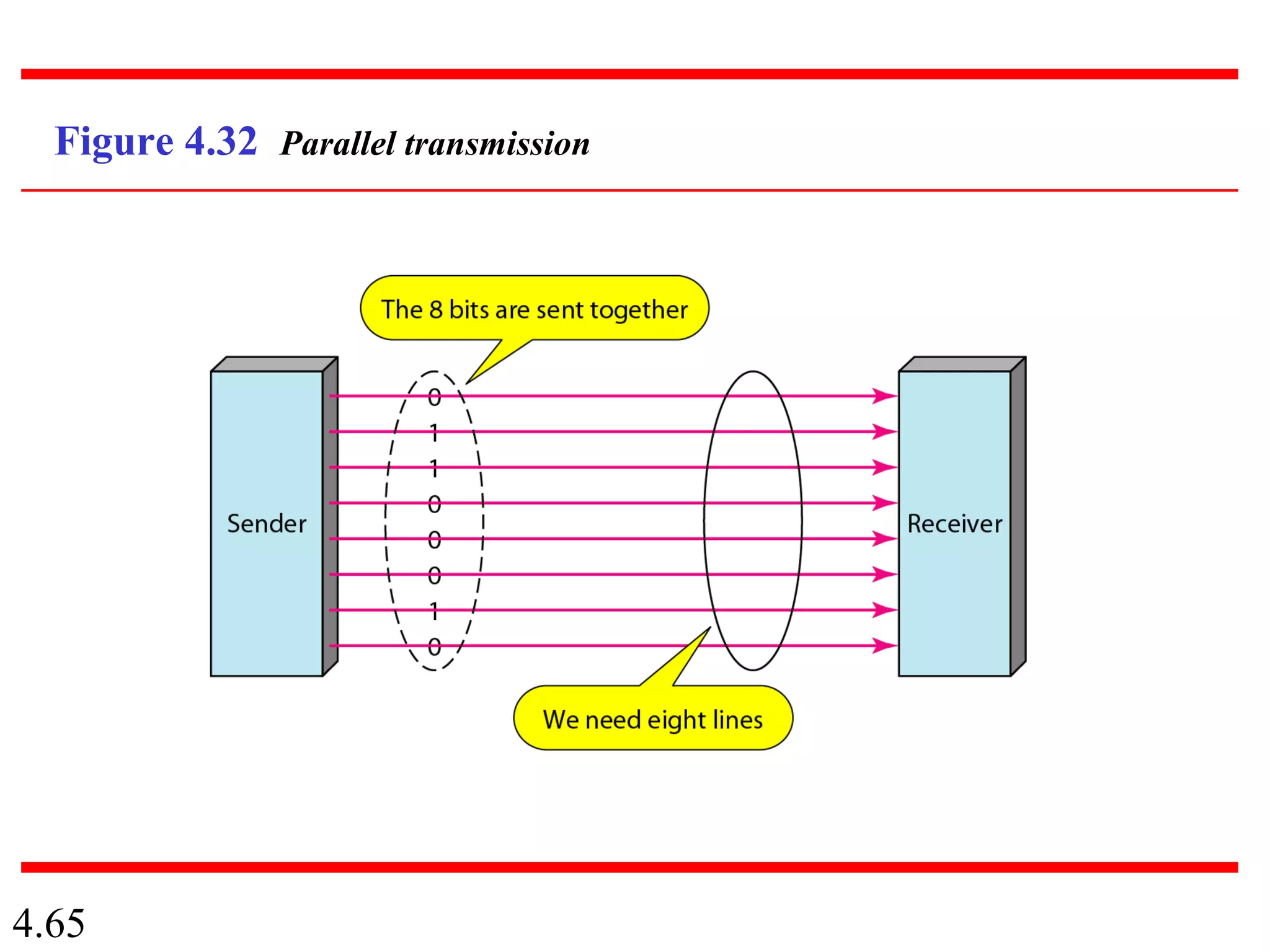
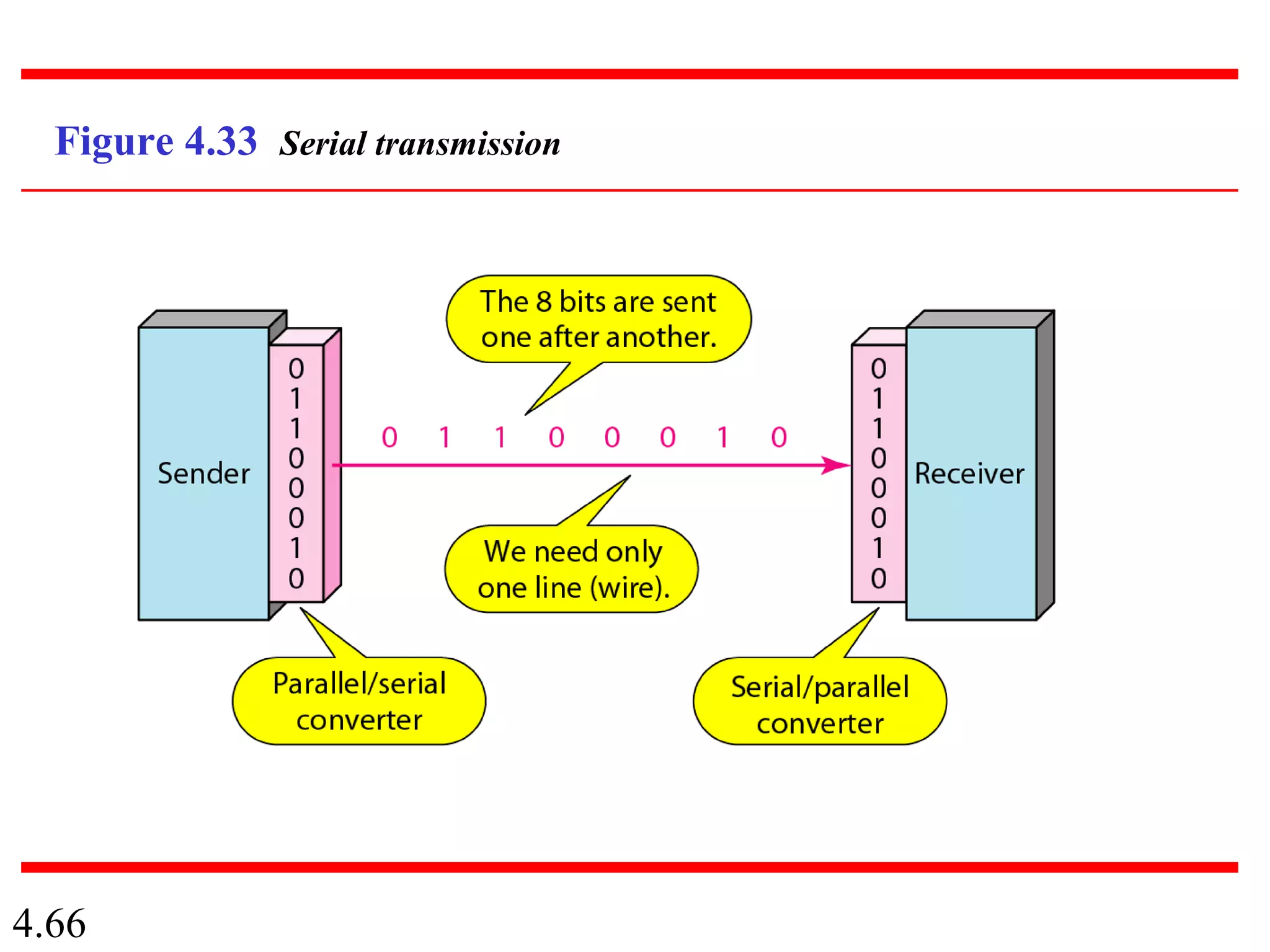
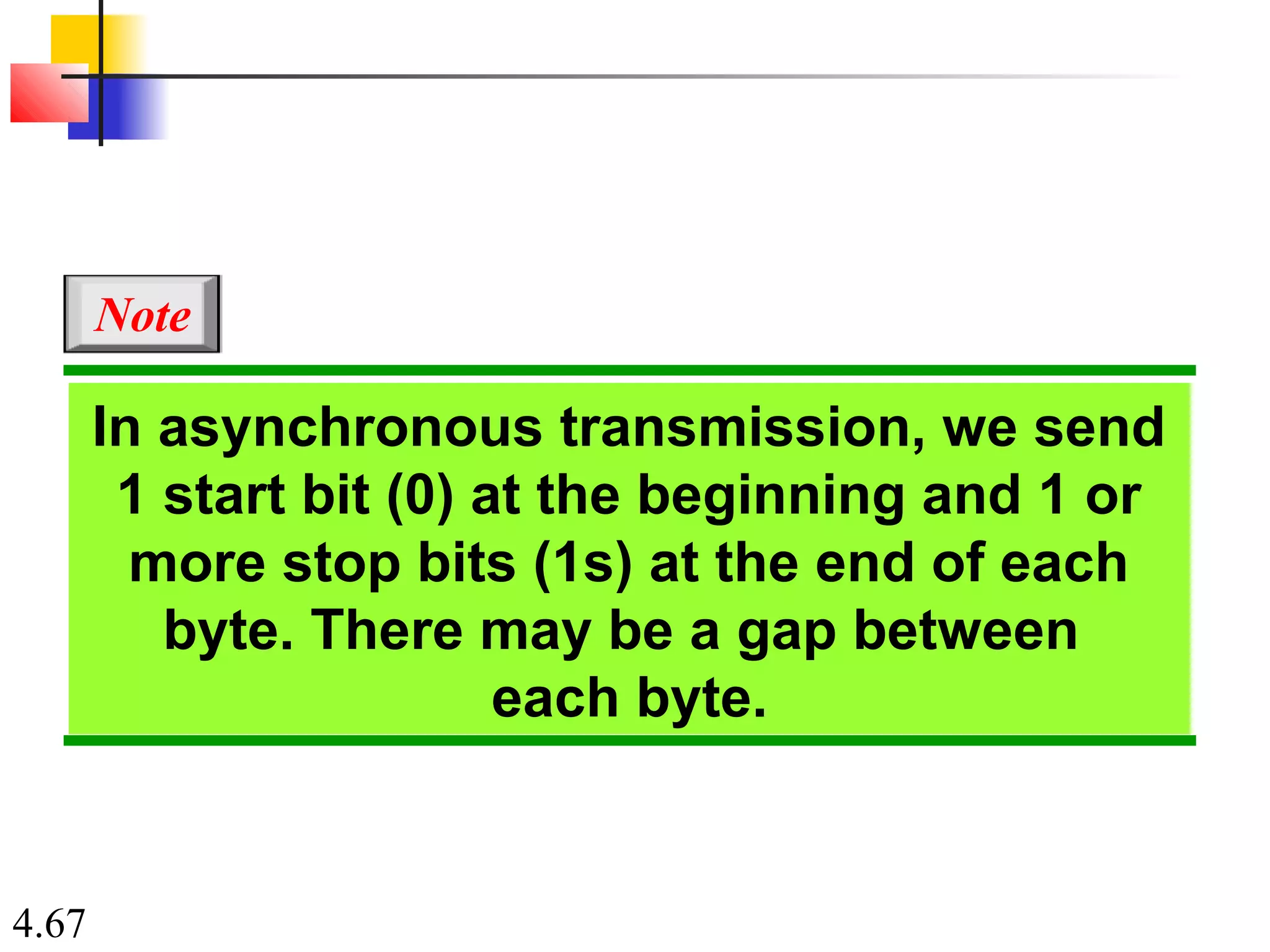
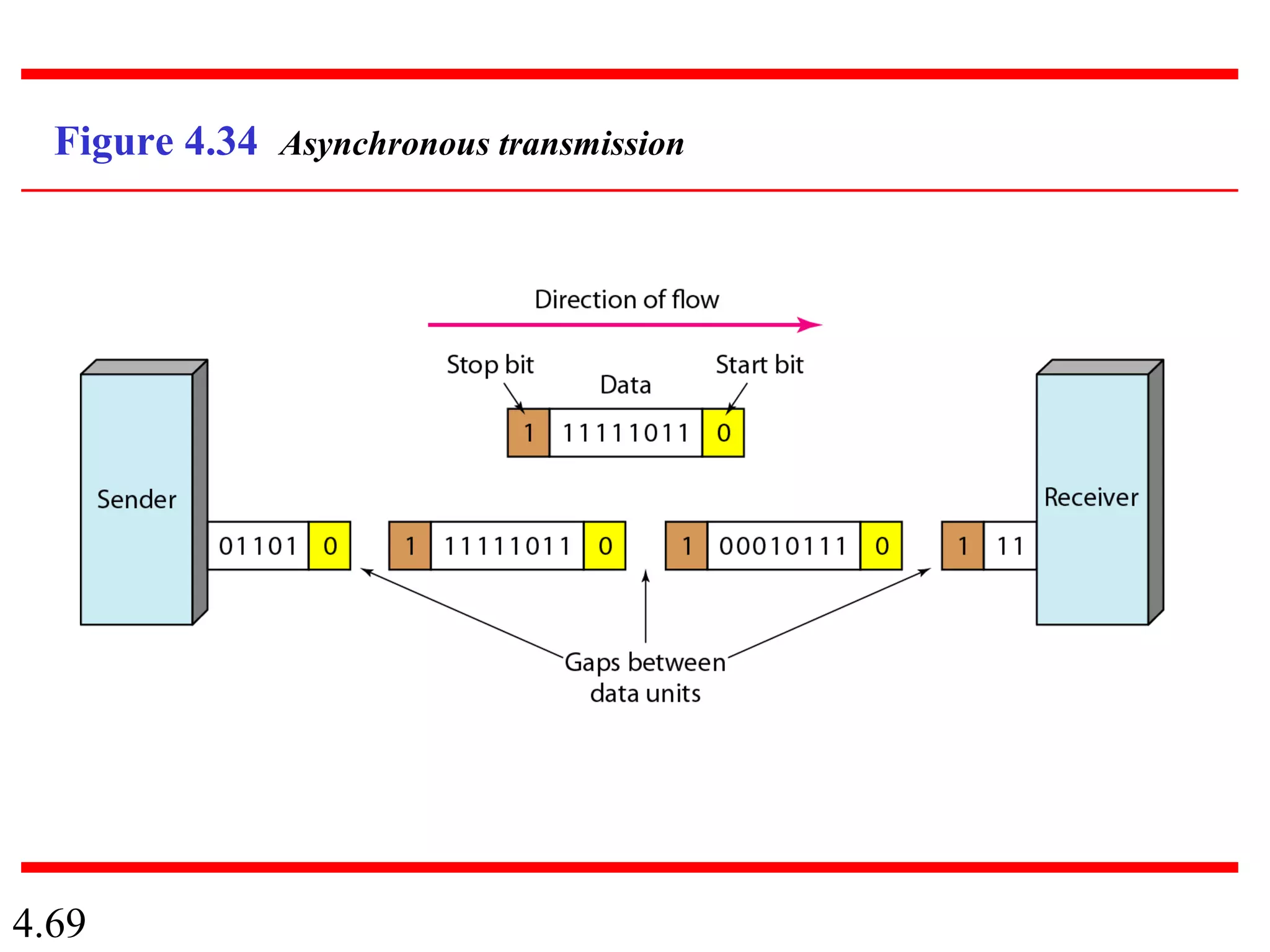
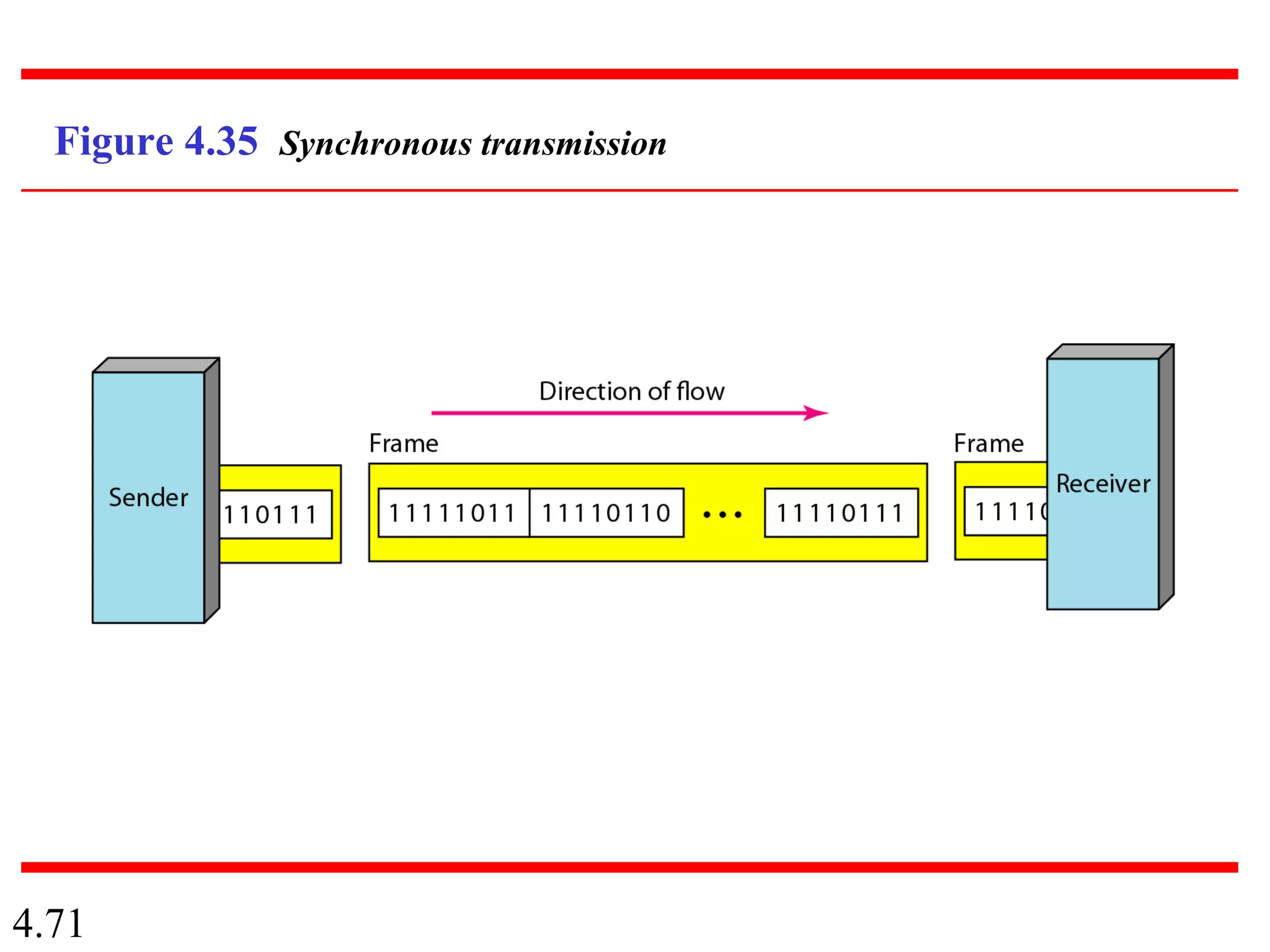
This document summarizes different techniques for digital transmission and conversion. It discusses digital-to-digital conversion through line coding, block coding, and scrambling. It also covers analog-to-digital conversion using pulse code modulation and delta modulation. Finally, it examines different transmission modes including parallel, asynchronous serial, synchronous serial, and isochronous serial transmission. The document contains diagrams and examples to illustrate key concepts in digital signal processing.