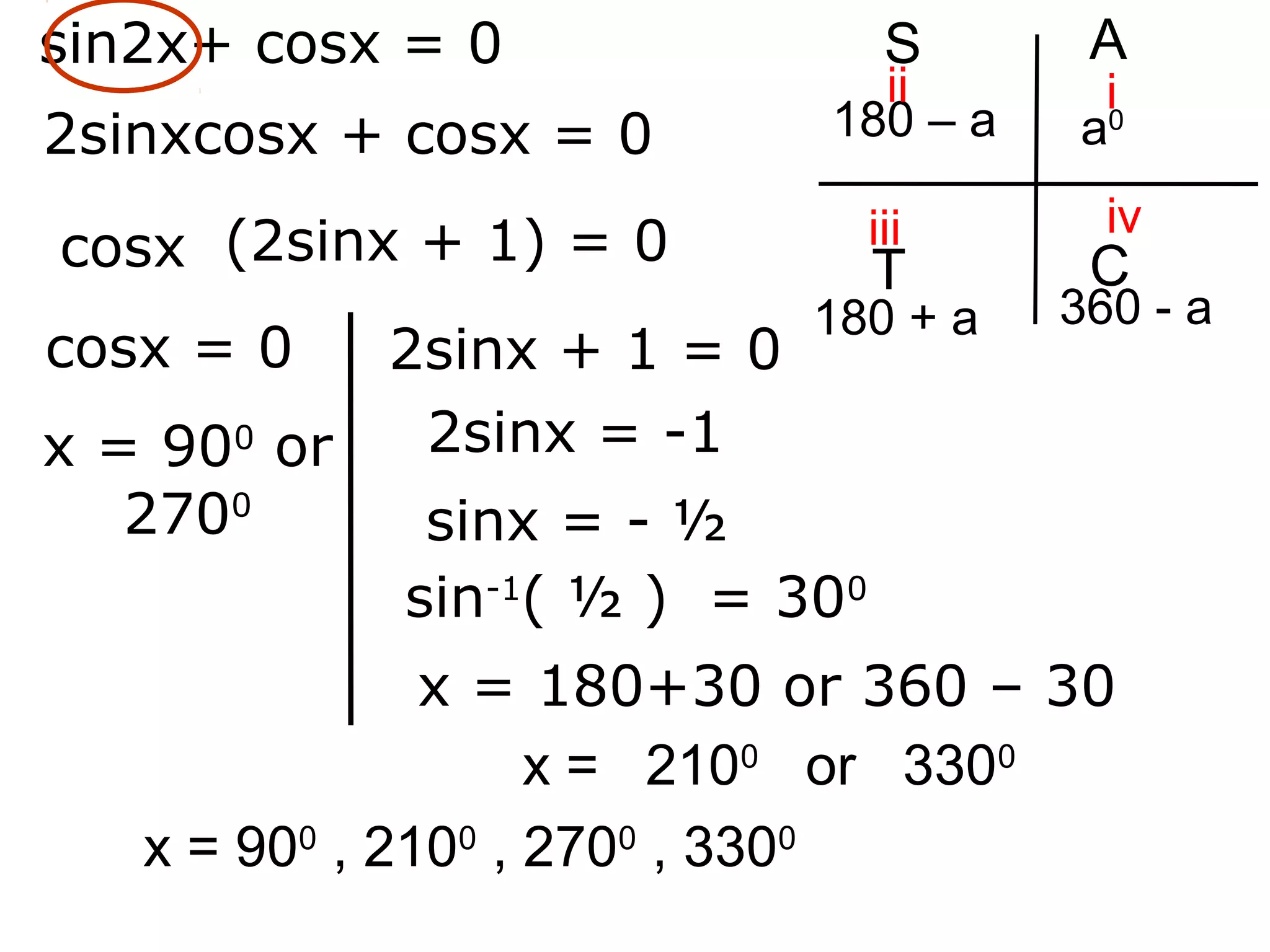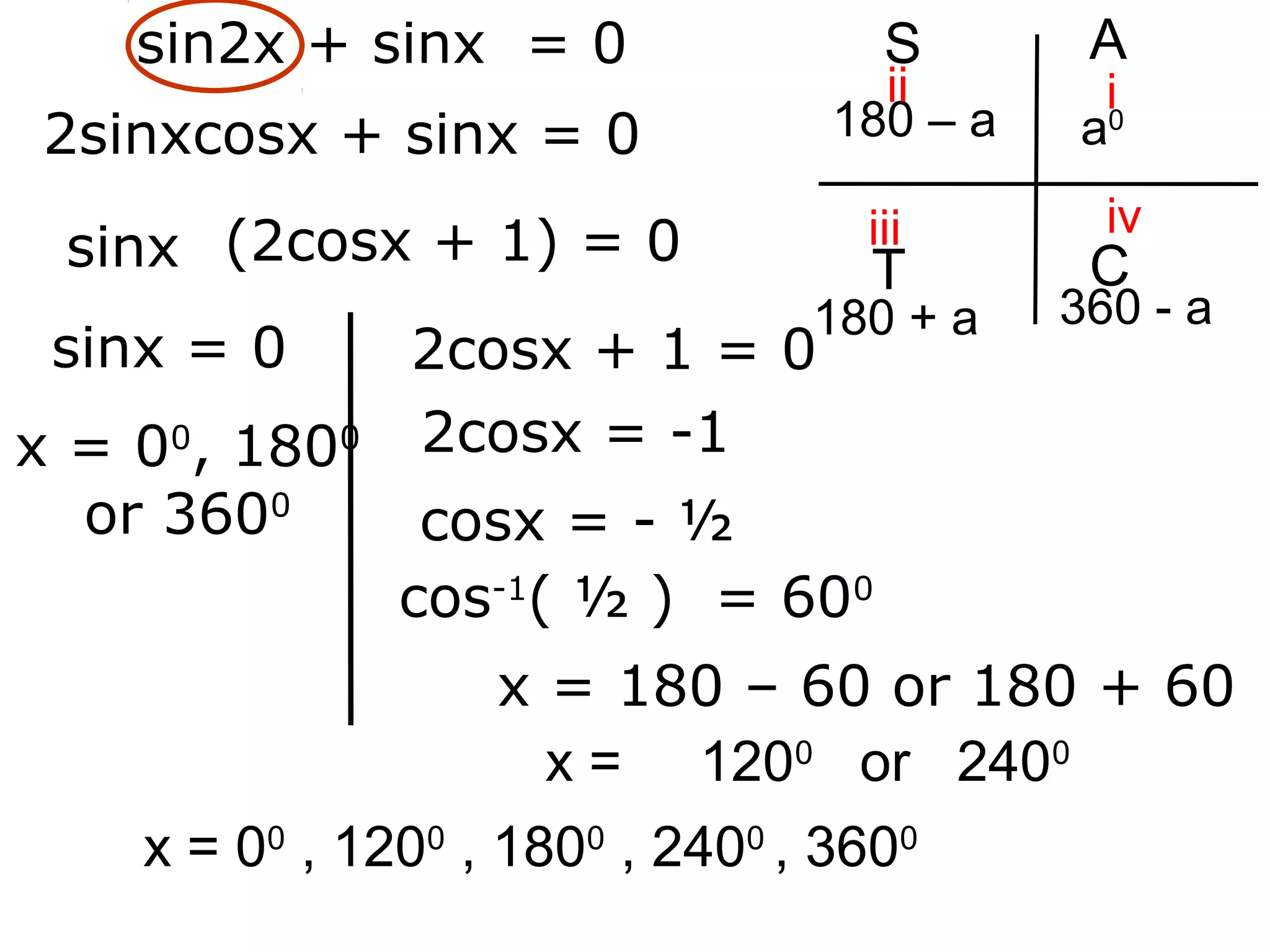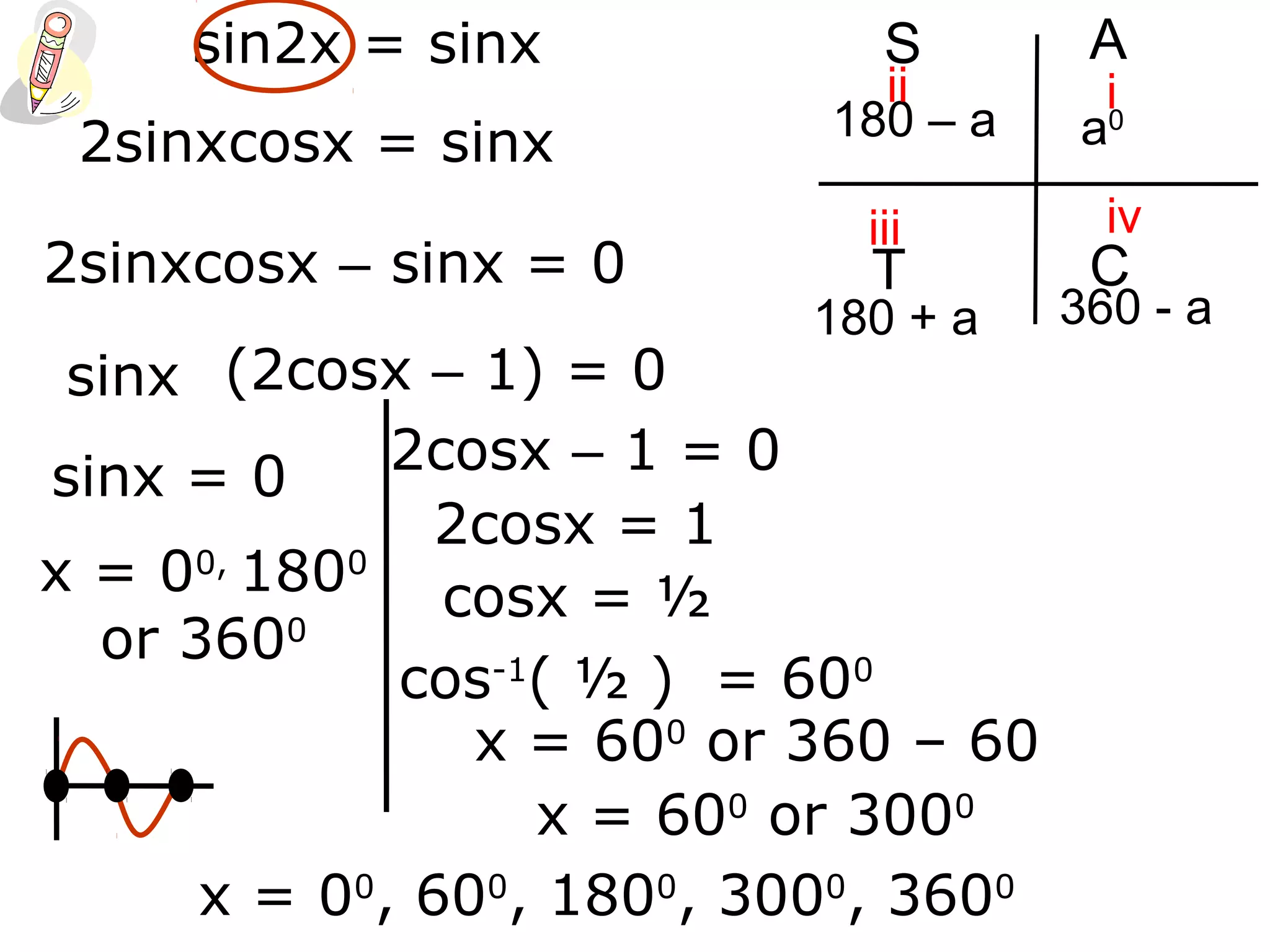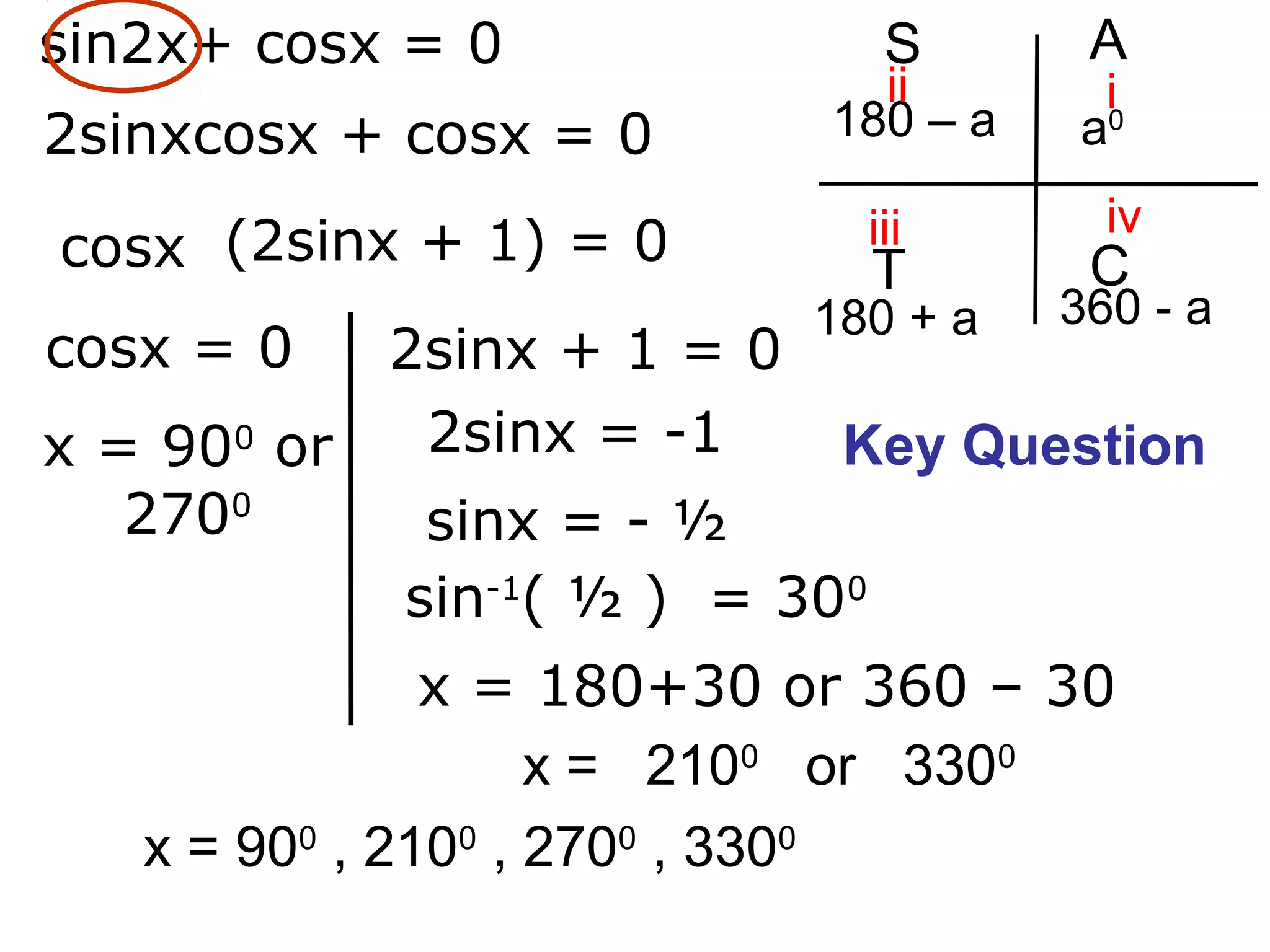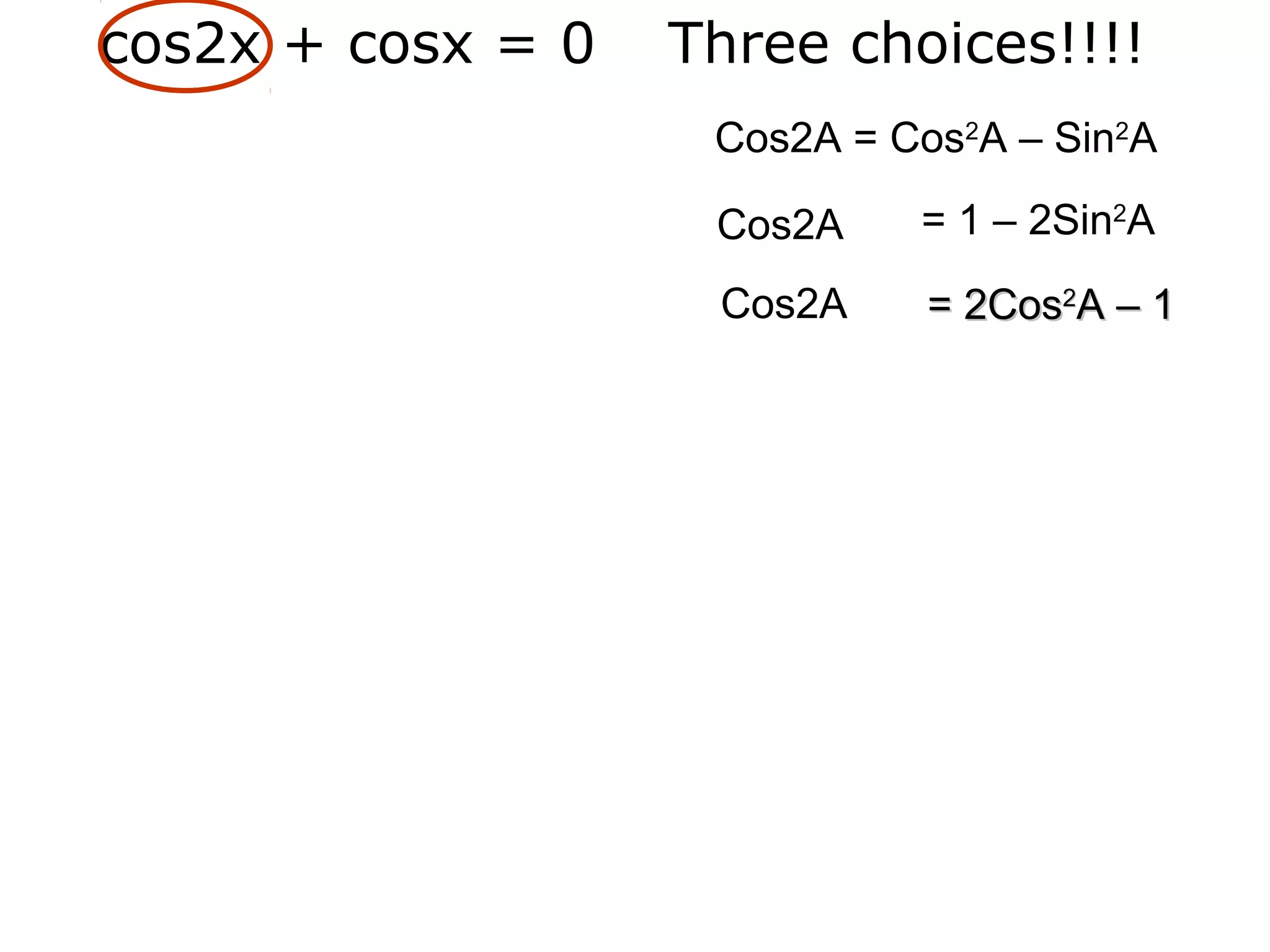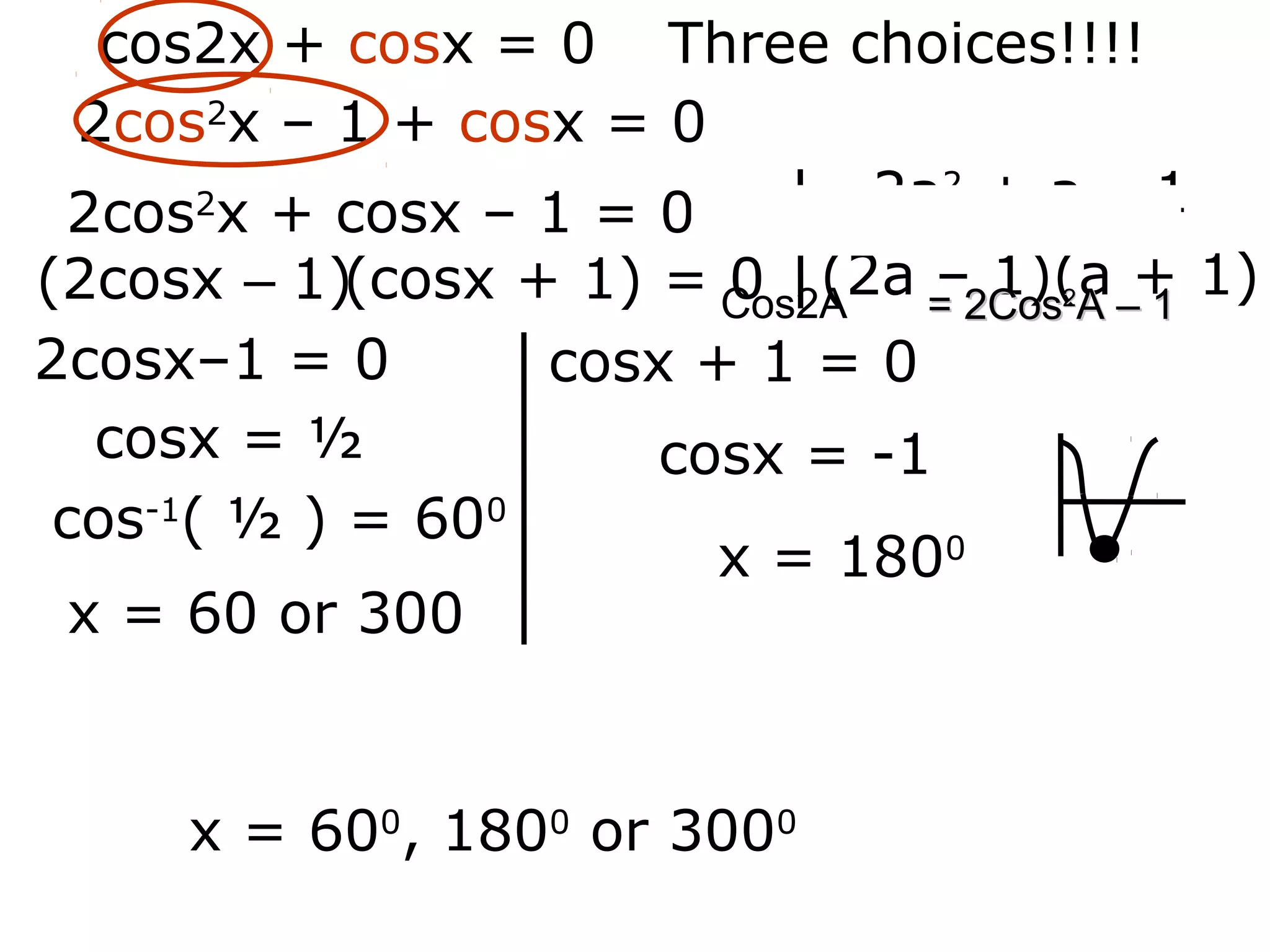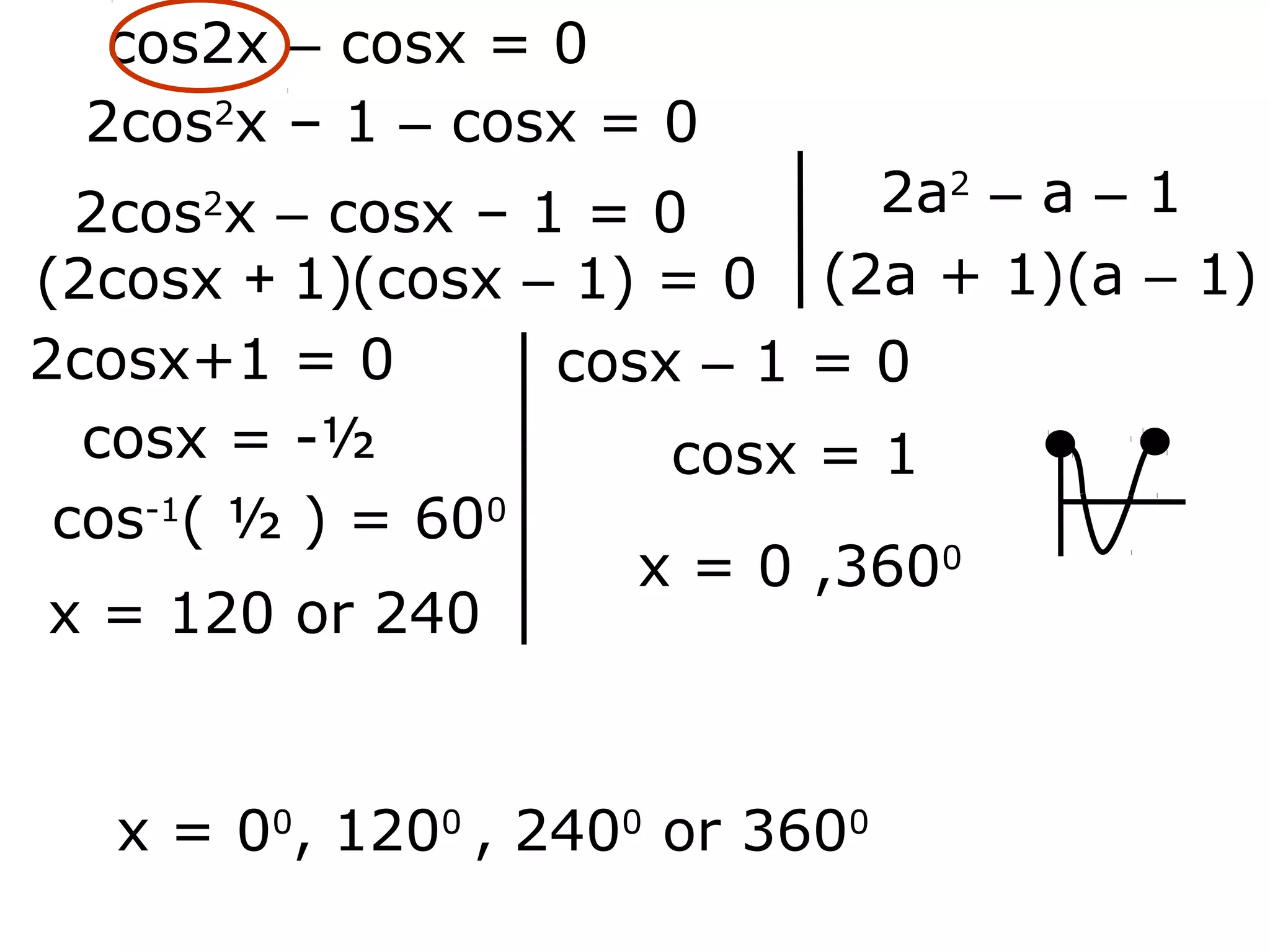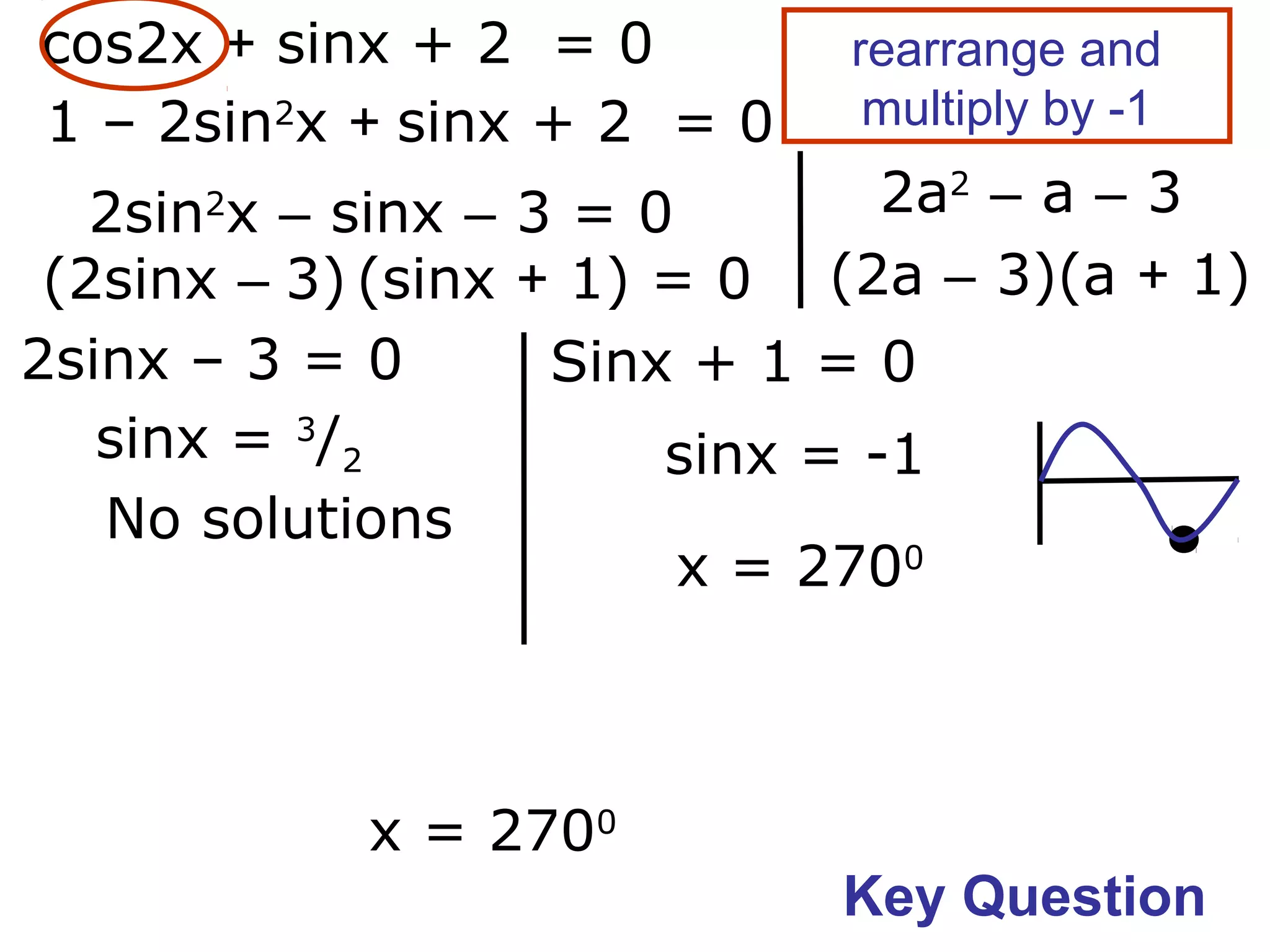1) The document discusses solving trigonometric equations using compound angle formulas and double angle formulas. 2) It provides examples of using these formulas to solve equations such as sin2x + cosx = 0, 2sinxcosx + cosx = 0, and cos2x - sinx = 0. 3) The key steps are to use a double angle formula to get one side equal to zero, factorize the equation, and then solve the resulting trigonometric mini equations.

1. Block 3
Solving Trig Equations
and Compound Angle Formulas

2. What is to be learned?
• How to use compound angle formulas to
solve more difficult trig equations

3. a0180 – a
180 + a 360 - a
iii
iii iv
CT
ASsin2x+ cosx = 0
2sinxcosx + cosx = 0
(2sinx + 1) = 0
cosx = 0 2sinx + 1 = 0
2sinx = -1
sinx = - ½
sin-1
( ½ ) = 300
x = 180+30 or 360 – 30
x = 900
or
2700
cosx
x = 2100
or 3300
x = 900
, 2100
, 2700
, 3300

4. a0180 – a
180 + a 360 - a
iii
iii iv
CT
ASsin2x + sinx = 0
2sinxcosx + sinx = 0
(2cosx + 1) = 0
sinx = 0 2cosx + 1 = 0
2cosx = -1
cosx = - ½
cos-1
( ½ ) = 600
x = 180 – 60 or 180 + 60
x = 00
, 1800
or 3600
sinx
x = 1200
or 2400
x = 00
, 1200
, 1800
, 2400
, 3600

5. Trig Equations and Double Angles
• Use double angle formula
• Get one side to zero
• Factorise
• Solve mini trig equations
(exact angles and wee trig graphs handy)

6. a0180 – a
180 + a 360 - a
iii
iii iv
CT
ASsin2x = sinx
2sinxcosx – sinx = 0
(2cosx – 1) = 0
sinx = 0 2cosx – 1 = 0
2cosx = 1
cosx = ½
cos-1
( ½ ) = 600
x = 600
or 360 – 60
x = 00,
1800
or 3600
sinx
2sinxcosx = sinx
x = 00
, 600
, 1800
, 3000
, 3600
x = 600
or 3000

7. a0180 – a
180 + a 360 - a
iii
iii iv
CT
ASsin2x+ cosx = 0
2sinxcosx + cosx = 0
(2sinx + 1) = 0
cosx = 0 2sinx + 1 = 0
2sinx = -1
sinx = - ½
sin-1
( ½ ) = 300
x = 180+30 or 360 – 30
x = 900
or
2700
cosx
x = 2100
or 3300
x = 900
, 2100
, 2700
, 3300
Key Question

8. cos2x + cosx = 0 Three choices!!!!
Cos2A = 1 – 2Sin2
A
= 2Cos= 2Cos22
A – 1A – 1Cos2A
Cos2A = Cos2
A – Sin2
A

9. cos2x + cosx = 0
2cos2
x – 1 + cosx = 0
2cos2
x + cosx – 1 = 0 2a2
+ a – 1
(2a – 1)(a + 1)(2cosx – 1)(cosx + 1) = 0
2cosx–1 = 0 cosx + 1 = 0
cosx = ½ cosx = -1
cos-1
( ½ ) = 600
x = 1800
x = 60 or 300
x = 600
, 1800
or 3000
Three choices!!!!
Cos2A = 1 – 2Sin2
A
= 2Cos= 2Cos22
A – 1A – 1Cos2A
Cos2A = Cos2
A – Sin2
A

10. cos2x – cosx = 0
2cos2
x – 1 – cosx = 0
2cos2
x – cosx – 1 = 0 2a2
– a – 1
(2a + 1)(a – 1)(2cosx + 1)(cosx – 1) = 0
2cosx+1 = 0 cosx – 1 = 0
cosx = -½ cosx = 1
cos-1
( ½ ) = 600
x = 0 ,3600
x = 120 or 240
x = 00
, 1200
, 2400
or 3600

11. For cos2x substitute the formula
that will leave equation all sine or all cos.

12. cos2x – sinx = 0
1 – 2sin2
x – sinx = 0
2sin2
x + sinx – 1 = 0 2a2
+ a – 1
(2a – 1)(a + 1)(2sinx – 1) (sinx + 1) = 0
2sinx – 1 = 0 Sinx + 1 = 0
sinx = ½ sinx = -1
sin-1
( ½ ) = 300
x = 2700
x = 300
or 1500
x = 300
, 1500
or 2700
rearrange and
multiply by -1

13. cos2x + sinx + 2 = 0
1 – 2sin2
x + sinx + 2 = 0
2sin2
x – sinx – 3 = 0 2a2
– a – 3
(2a – 3)(a + 1)(2sinx – 3) (sinx + 1) = 0
2sinx – 3 = 0 Sinx + 1 = 0
sinx = 3
/2 sinx = -1
No solutions
x = 2700
x = 2700
rearrange and
multiply by -1
Key Question