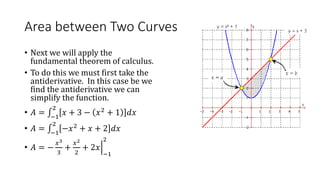
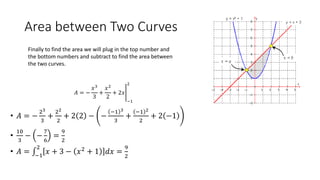
The document discusses calculating the area between two curves from x=-1 to x=2. It provides the following steps: 1) Find the interval between where the two curves intersect, which is from x=-1 to x=2. 2) Apply the fundamental theorem of calculus to find the antiderivative of f(x) - g(x) over that interval. 3) Evaluate the antiderivative at the upper and lower bounds and take the difference, which gives the area between the curves as 9/2.

1. Area between Two Curves
• 𝐴 = 𝑎
𝑏
𝑓 𝑥 − 𝑔(𝑥) 𝑑𝑥 as long as 𝑓 𝑥 ≥ 𝑔(𝑥)
• First we need to find the interval, in this example
it is obvious the graphs intersect at −1,2 and
(2,5) so we will be using the interval −1,2
• Remember to always use the x-coordinates to
represent the interval
• In this case we are finding the area between the 2
curves from x = -1 to x = 2

2. Area between Two Curves
• Next we will apply the
fundamental theorem of calculus.
• To do this we must first take the
antiderivative. In this case be we
find the antiderivative we can
simplify the function.
• 𝐴 = −1
2
𝑥 + 3 − 𝑥2
+ 1 𝑑𝑥
• 𝐴 = −1
2
−𝑥2
+ 𝑥 + 2 𝑑𝑥
• 𝐴 = −
𝑥3
3
+
𝑥2
2
+ 2𝑥
−1
2

3. Area between Two Curves
• 𝐴 = −
23
3
+
22
2
+ 2 2 − −
−1 3
3
+
−1 2
2
+ 2 −1
•
10
3
− −
7
6
=
9
2
• 𝐴 = −1
2
𝑥 + 3 − 𝑥2 + 1 𝑑𝑥 =
9
2
Finally to find the area we will plug in the top number and
the bottom numbers and subtract to find the area between
the two curves.
𝐴 = −
𝑥3
3
+
𝑥2
2
+ 2𝑥
−1
2