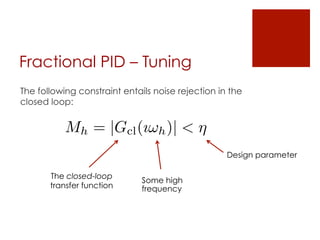
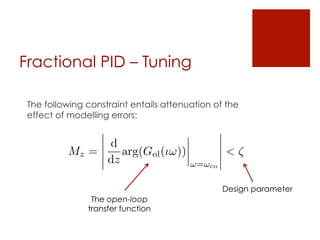
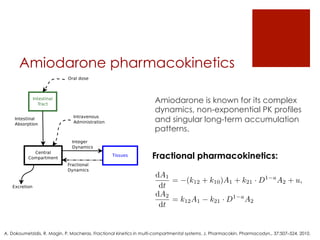
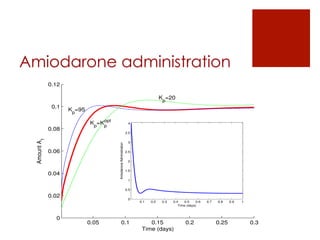
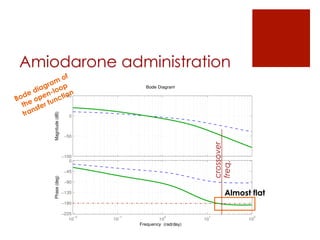
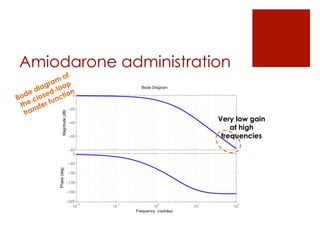
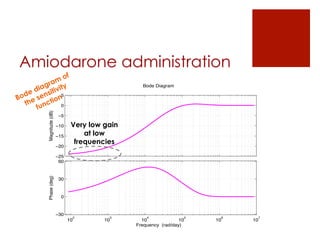
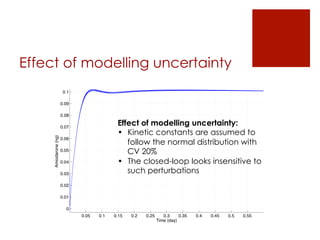
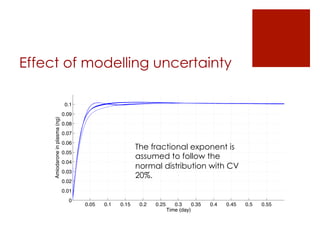
This document summarizes the design of a fractional PID controller to adjust amiodarone concentration levels intravenously. Amiodarone exhibits complex, fractional pharmacokinetics. A fractional PID controller was tuned using constraints to ensure stability, noise rejection, and insensitivity to modeling errors. Simulations showed the closed-loop system was stable and resilient to disturbances with the controller able to filter noise and be insensitive to uncertainties in kinetic parameters.

1. Controlled drug
administration by a
fractional PID
Pantelis Sopasakis*,** and Haralambos Sarimveis**
* IMT Institute for Advanced Studies Lucca
** School of Chemical Engineering, NTU Athens

2. Motivation
About: Amiodarone is an antiarrhythmic agent
exhibiting highly nonlinear and complex
dynamics.
Scope: Design a feedback controller to adjust
the concentration of amiodarone to desired
levels when administered intra-venously.
Pulmonary fibrosis
Skin
pigmentation
Side-effects due
to accumulation
A. Dokoumetzidis & P. Macheras. IVIVC of controlled release formulations: Physiological-dynamical reasons for their
failure. J. Control. Release, 129(2): 76–78, 2008.

3. The Caputo Fractional
Derivative
The Cauchy formula gives
the n-th order integral of a
function:
(In
f)(t) =
1
(n 1)!
Z t
0
(t ⌧)n 1
f(⌧)d⌧

4. The Caputo Fractional
Derivative
which can be generalized
for any positive real order α
as follows:
(I↵
f)(t) =
1
(↵)
Z t
0
(t ⌧)↵ 1
f(⌧)d⌧
The Cauchy formula gives
the n-th order integral of a
function:
(In
f)(t) =
1
(n 1)!
Z t
0
(t ⌧)n 1
f(⌧)d⌧

5. by means of which we
introduce the Caputo
fractional-order derivative:
(D↵
f)(t) = Im ↵ dm
f(t)
dtm
with m = b↵c
The Caputo Fractional
Derivative
which can be generalized
for any positive real order α
as follows:
(I↵
f)(t) =
1
(↵)
Z t
0
(t ⌧)↵ 1
f(⌧)d⌧
The Cauchy formula gives
the n-th order integral of a
function:
(In
f)(t) =
1
(n 1)!
Z t
0
(t ⌧)n 1
f(⌧)d⌧

6. Interesting properties
The Caputo fractional derivative:
• Extends the standard integer-order derivative to real
orders,
• Preserves analiticity & is a linear operator,
• Has the semigroup property and
• Is a non-local operator
i.e., it takes into account
the whole history of the
function.
R. Hilfer. Applications Of Fractional Calculus In Physics. World Scientific, 2000. ISBN 978-981-02-3457-7.

7. Interesting properties
The Laplace transform of fractional derivatives is
remniscient of the one for integer-order derivatives:
L[D↵
f](s) = s↵
F(s)
m 1X
k=0
s↵ k 1
f(k)
(0)
R. Hilfer. Applications Of Fractional Calculus In Physics. World Scientific, 2000. ISBN 978-981-02-3457-7.

8. Fractional Dynamical
Systems
Fractional derivatives and integrals give rise to
fractional dynamical systems:
H(D↵1
, . . . , D↵n
)x = T(D 1
, . . . , D m
)u
Applying the Laplace transform, linear
fractional systems can be described by a
transfer function:
where P and Q are fractional polynomials.
G(s) =
X(s)
U(s)
=
P(s)
Q(s)
BIBO Stability: The Bode stability
criterion applies to fractional
dynamical systems as is!!!

9. Fractional PID
A fractional PID controller is a fractional
system with transfer function:
Gc(s) = Kp +
Ki
s
+ Kdsµ
Tuning following the method of Valerio and da Costa
Minimisation of ITAE:
J?
itae = min
Kp,Ki,Kd, ,µ
Jitae
Jitae =
Z 1
0
⌧|✏(⌧)|d⌧
D. Valerio and J.S. da Costa, Tuning of fractional PID controllers with Ziegler-Nichols-type rules, Sign. proc., 86(1), 2006

10. Fractional PID
Tuning following the method of Valerio and da Costa
Minimisation of ITAE:
J?
itae = min
Kp,Ki,Kd, ,µ
Jitae
Jitae =
Z 1
0
⌧|✏(⌧)|d⌧
A fractional PID controller is a fractional
system with transfer function:
Gc(s) = Kp +
Ki
s
+ Kdsµ
Subject to additional constraints so that:
• The closed loop is BIBO-stable
• In-loop and external noise is attenuated
• Modelling errors are rejected
• Low frequency output disturbances are dumped
• The gain and phase margins have desired values
D. Valerio and J.S. da Costa, Tuning of fractional PID controllers with Ziegler-Nichols-type rules, Sign. proc., 86(1), 2006

11. Fractional PID – Tuning
The following constraint entails noise rejection in the
closed loop:
The closed-loop
transfer function
Some high
frequency
Mh = |Gcl(ı!h)| < ⌘
Design parameter

12. Fractional PID – Tuning
The following constraint entails attenuation of the
effect of modelling errors:
The open-loop
transfer function
Design parameter
Mz =
d
dz
arg(Gol(◆!))
!=!co
< ⇣

13. Fractional PID – Tuning
The following constraint is imposed so that low-
frequency disturbances are rejected:
M` = |Gsens(ı!`)| < #
Design parameter
The sensitivity transfer
function defined as:
Gsens(s) =
1
1 + Gol(s)
Some low
frequency

14. Simulations
Simulations were carried out using the Oustaloup
Filter: Fractional-order transfer functions are
approximated by rational in a range of frequencies.
A. Oustaloup, F. Levron, B. Mathieu and F.M. Nanot, Frequency-band complex non-integer differentiator: characterization and synthesis, IEEE
Transactions on Circuits & Systems I: Fund. Theory and Appl. 47(1): 25-39, 2000.

15. Amiodarone pharmacokinetics
Amiodarone is known for its complex
dynamics, non-exponential PK profiles
and singular long-term accumulation
patterns.
A. Dokoumetzidis, R. Magin, P. Macheras. Fractional kinetics in multi-compartmental systems. J. Pharmacokin. Pharmacodyn., 37:507–524, 2010.
dA1
dt
= (k12 + k10)A1 + k21 · D1 a
A2 + u,
dA2
dt
= k12A1 k21 · D1 a
A2
Fractional pharmacokinetics:

16. Amiodarone administration
A fractional PID was tuned with the above method and
lead to:
• A phase margin of 98° and a gain margin of 43.9db
• The closed-loop transfer function gives < -60db at high
frequencies (higher than 100rad/day)
• The sensitivity function gives < -20db at low frequencies
(lower than 0.1rad/day)
• The open-loop function has a low derivative at the
crossover frequency (Mz = 0.0087).

17. Amiodarone administration
0.05 0.1 0.15 0.2 0.25 0.3
0
0.02
0.04
0.06
0.08
0.1
0.12
Kp
=20
Kp
=95
Kp
=Kp
opt
Time (days)
AmountA1
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.5
1
1.5
2
2.5
3
3.5
4
Time (days)
AmiodaroneAdministration

18. Amiodarone administration
100
50
0
50
Magnitude(dB)
10
2
10
1
10
0
10
1
10
2
225
180
135
90
45
0
Phase(deg)
Bode Diagram
Frequency (rad/day)
Almost flat
crossover
freq.

19. Amiodarone administration
80
60
40
20
0
Magnitude(dB)
10
2
10
1
10
0
10
1
10
2
225
180
135
90
45
0
Phase(deg)
Bode Diagram
Frequency (rad/day)
Very low gain
at high
frequencies

20. Amiodarone administration
−25
−20
−15
−10
−5
0
5
Magnitude(dB)
10
2
10
3
10
4
10
5
10
6
10
7
−30
0
30
60
Phase(deg)
Bode Diagram
Frequency (rad/day)
Very low gain
at low
frequencies

21. 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Time (day)
Amiodarone(ng)
Effect of modelling uncertainty
Effect of modelling uncertainty:
• Kinetic constants are assumed to
follow the normal distribution with
CV 20%
• The closed-loop looks insensitive to
such perturbations

22. Effect of modelling uncertainty
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Time (day)
Amiodaroneinplasma(ng)
The fractional exponent is
assumed to follow the
normal distribution with CV
20%.

23. Recapitulation
¡ Amiodarone exhibits fractional pharmacokinetics,
¡ A fractional PID was designed for the feedback
control of amiodarone,
¡ The controlled system was stable, resilient to
disturbances, able to filter out noise and insensitive
to modelling errors.

24. Thank you for your attention!
This work was partly funded by project 11SYN.10.1152, which was co-financed by the European Union and Greece, Operational
Program “Competitiveness & Entrepreneurship”, NSFR 20072013 in the context of GSRT-National action “Cooperation”.