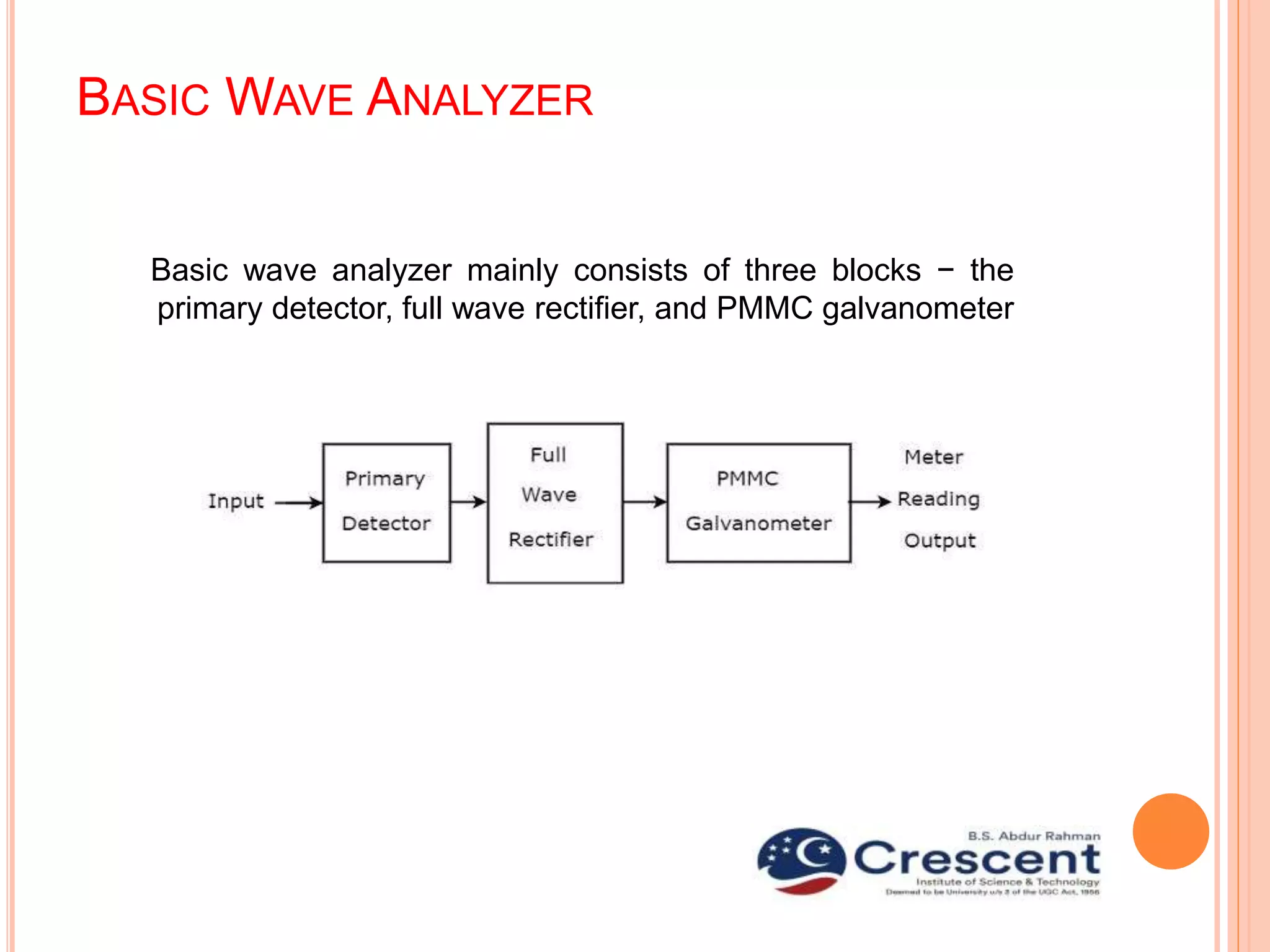
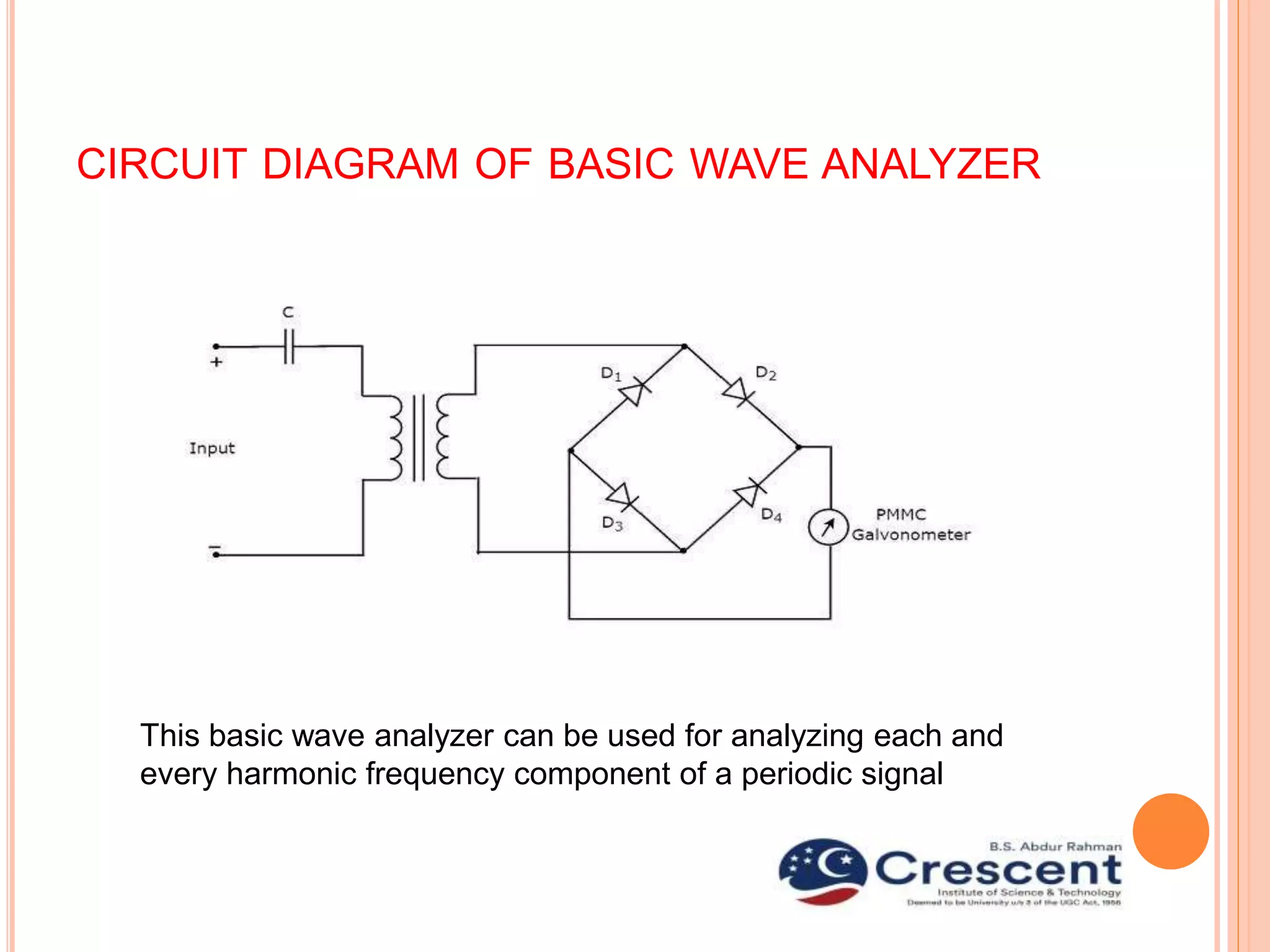
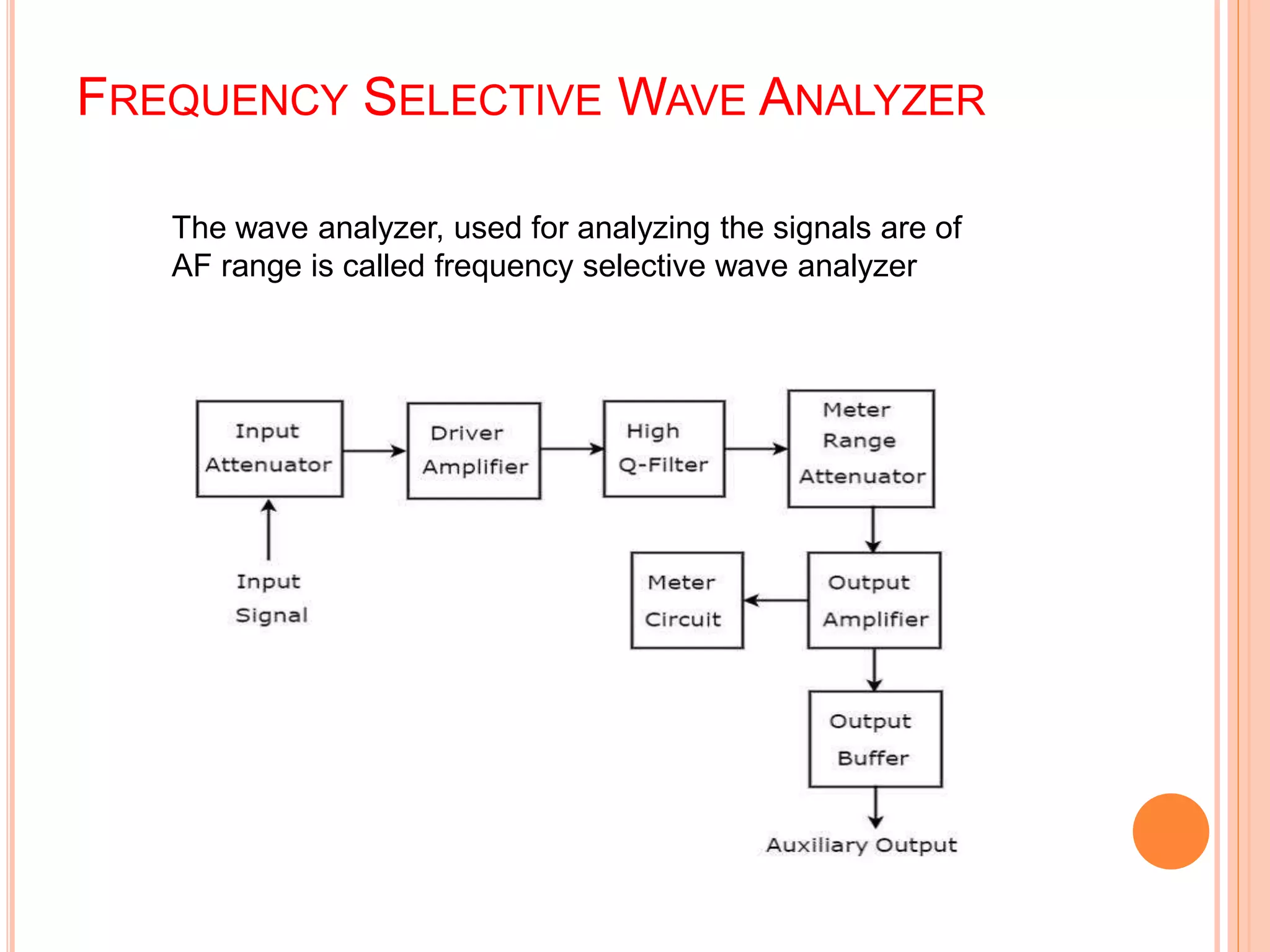
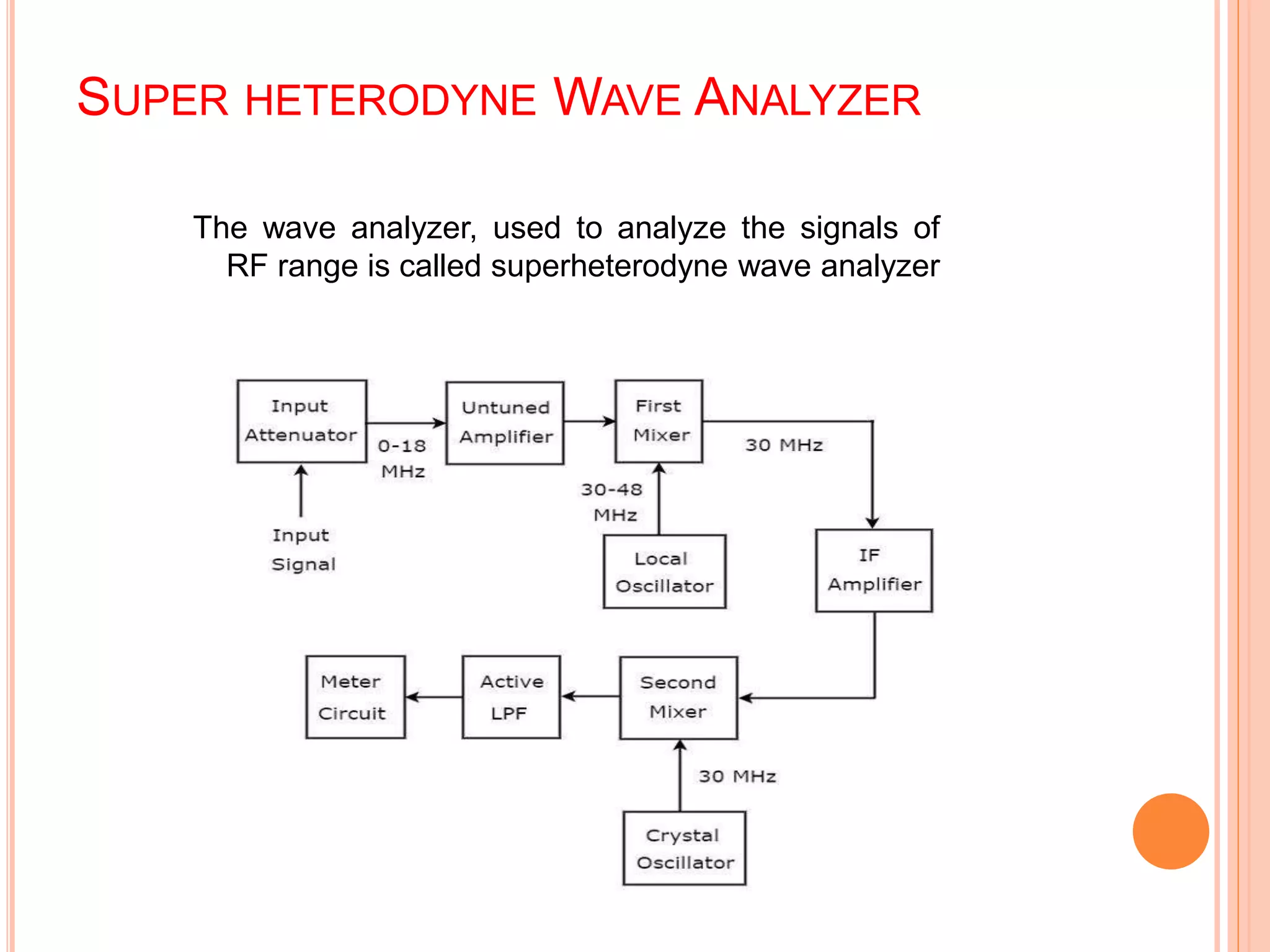
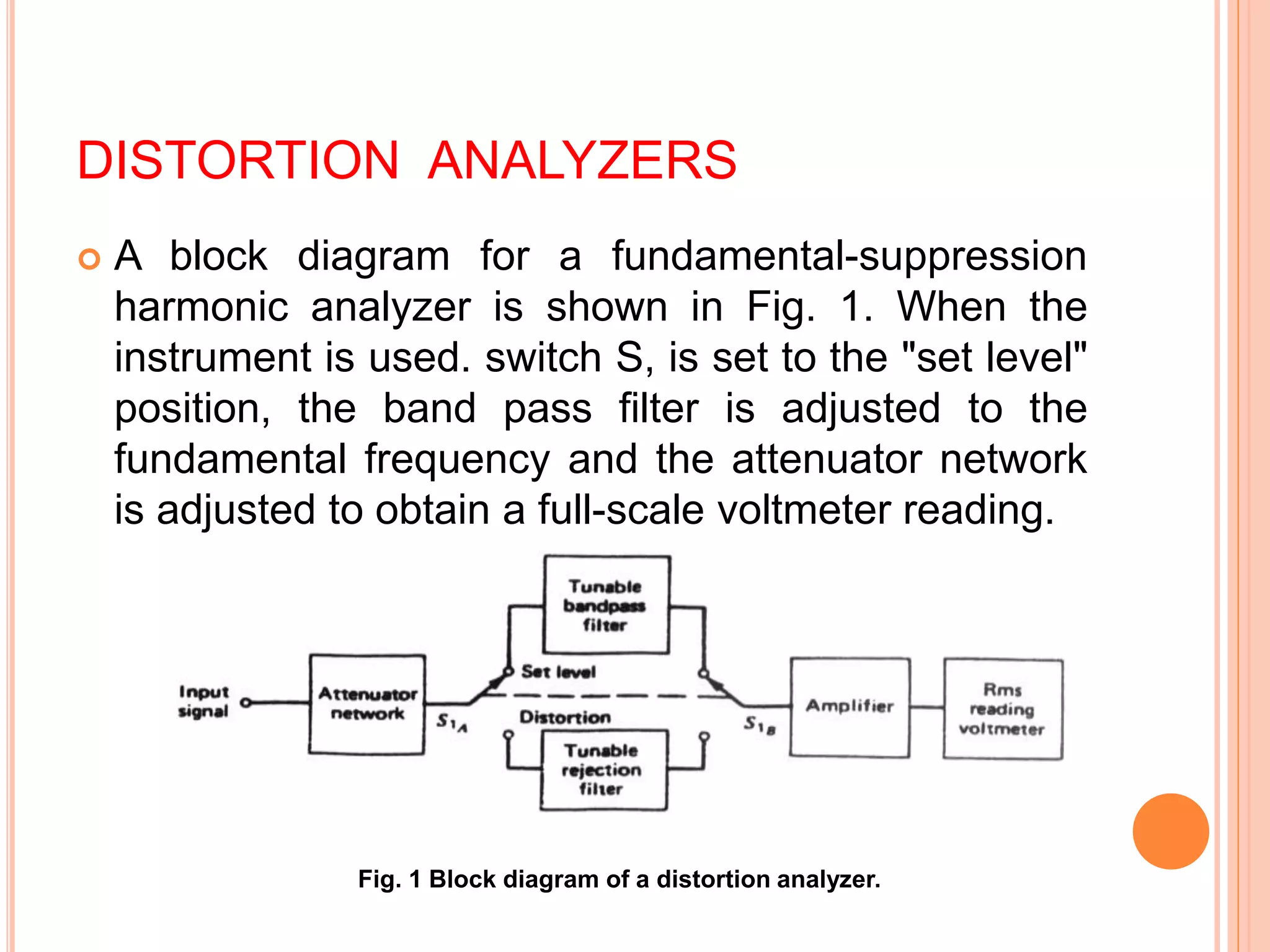
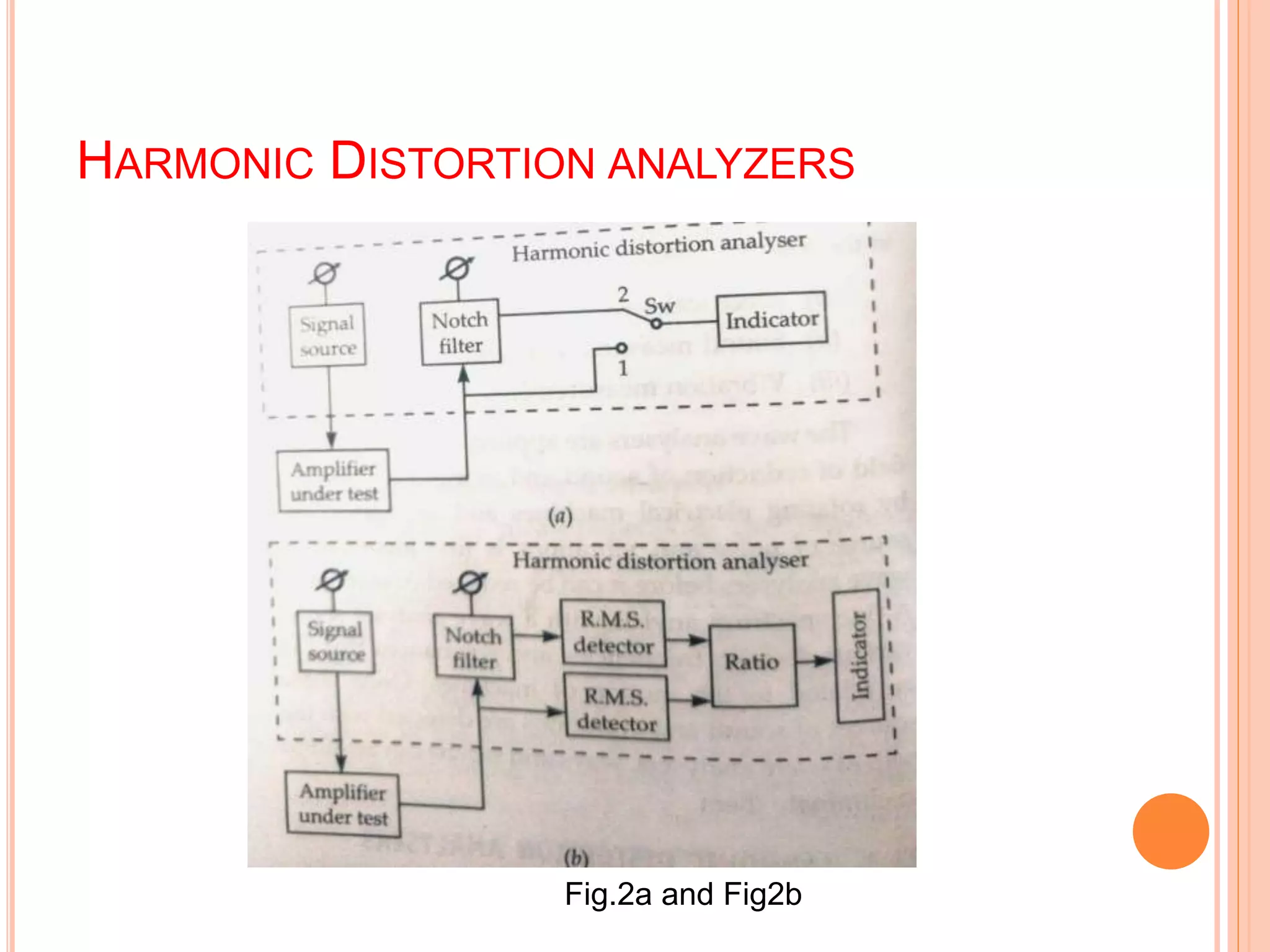
This document provides information about wave analyzers and harmonic distortion analyzers. It discusses the basic components and functions of a basic wave analyzer, which consists of a primary detector, full wave rectifier, and galvanometer. It also describes frequency selective and heterodyne wave analyzers. The document then covers harmonic distortion analyzers, defining total harmonic distortion as a percentage based on harmonic and fundamental signal amplitudes. It provides an example calculation and discusses how harmonic distortion analyzers measure THD using filters to separate the fundamental and harmonic components.

1. MODULE V
WAVE ANALYZERS
G.Anitha
Asst.Professor (Senior Grade)
B S A Crescent Institute of Science and Technology

2. INTRODUCTION
 A wave analyzer is an instrument designed to
measure relative amplitudes of single frequency
components in a complex waveform. Basically, a
wave instrument acts as a frequency selective
voltmeter which is tuned to the frequency of one
signal while rejecting all other signal components.

3. BASIC WAVE ANALYZER
Basic wave analyzer mainly consists of three blocks − the
primary detector, full wave rectifier, and PMMC galvanometer

4. BASIC WAVE ANALYZER
 Primary Detector − It consists of an LC circuit. We
can adjust the values of inductor, L and capacitor, C
in such a way that it allows only the desired
harmonic frequency component that is to be
measured.
 Full Wave Rectifier − It converts the AC input into
a DC output.
 PMMC Galvanometer − It shows the peak value of
the signal, which is obtained at the output of Full
wave rectifier.

5. CIRCUIT DIAGRAM OF BASIC WAVE ANALYZER
This basic wave analyzer can be used for analyzing each and
every harmonic frequency component of a periodic signal

6. TYPES
 Frequency Selective Wave Analyzer
 Heterodyne wave analyzer

7. FREQUENCY SELECTIVE WAVE ANALYZER
The wave analyzer, used for analyzing the signals are of
AF range is called frequency selective wave analyzer

8. FUNCTION OF FREQUENCY SELECTIVE WAVE
ANALYZER
 Input Attenuator − The AF signal, which is to be analyzed is applied to
input attenuator. If the signal amplitude is too large, then it can be
attenuated by input attenuator.
 Driver Amplifier − It amplifies the received signal whenever necessary.
 High Q-filter − It is used to select the desired frequency and reject
unwanted frequencies. It consists of two RC sections and two filter
amplifiers & all these are cascaded with each other. We can vary the
capacitance values for changing the range of frequencies in powers of
10. Similarly, we can vary the resistance values in order to change the
frequency within a selected range.
 Meter Range Attenuator − It gets the selected AF signal as an input &
produces an attenuated output, whenever required.
 Output Amplifier − It amplifies the selected AF signal if necessary.
 Output Buffer − It is used to provide the selected AF signal to output
devices.
 Meter Circuit − It displays the reading of selected AF signal. We can
choose the meter reading in volt range or decibel range.

9. SUPER HETERODYNE WAVE ANALYZER
The wave analyzer, used to analyze the signals of
RF range is called superheterodyne wave analyzer

10. FUNCTION OF SUPER-HETERODYNE WAVE
ANALYZER
 The RF signal, which is to be analyzed is applied to the input attenuator.
If the signal amplitude is too large, then it can be attenuated by input
attenuator.
 Untuned amplifier amplifies the RF signal whenever necessary and it is
applied to first mixer.
 The frequency ranges of RF signal & output of Local oscillator are 0-18
MHz & 30-48 MHz respectively. So, first mixer produces an output,
which has frequency of 30 MHz. This is the difference of frequencies of
the two signals that are applied to it.
 IF amplifier amplifies the Intermediate Frequency (IF) signal, i.e. the
output of first mixer. The amplified IF signal is applied to second mixer.
 The frequencies of amplified IF signal & output of Crystal oscillator are
same and equal to 30MHz. So, the second mixer produces an output,
which has frequency of 0 Hz. This is the difference of frequencies of the
two signals that are applied to it.
 The cut off frequency of Active Low Pass Filter (LPF) is chosen as
1500 Hz. Hence, this filter allows the output signal of second mixer.
 Meter Circuit displays the reading of RF signal. We can choose the
meter reading in volt range or decibel range.

11. APPLICATIONS OF WAVE ANALYZERS
Wave analyzers have very important applications in
the following fields
 Electrical Measurements
 Sound measurements
 Vibration measurements

12. HARMONIC DISTORTION ANALYZERS
 Applying a sinusoidal signal to the input of an ideal
linear amplifier will produce a sinusoidal output
waveform. However, in most cases the output
waveform is not an exact replica of the input signal
because of various types of distortion.

13. DISTORTION ANALYZERS
 The extent to which the output waveform of an-
amplifier differs from the waveform at the input is a
measure of the distortion introduced by the inherent
nonlinear characteristics of active devices such as
bipolar or field-effect transistors or by passive
circuit components. The amount of distortion can be
measured with a distortion analyzer.

14. DISTORTION ANALYZERS
 When an amplifier is not operating in a linear
fashion, the output signal will be distorted.
Distortion caused by nonlinear operation is called
amplitude distortion or harmonic distortion. It can be
shown mathematically that an amplitude-distorted
sine wave is made up of pure sine-wave
components including the fundamental frequency f
of the input signal and harmonic multiples of the
fundamental frequency, 2f, 3f, 4f . . . , and so on.

15. DISTORTION ANALYZERS
 When harmonics are present in considerable
amount, their presence can be observed with an
oscilloscope. The waveform displayed will either
have unequal positive and negative peak values or
will exhibit a change in shape. In either case, the
oscilloscope will provide a qualitative check of
harmonic distortion. However. the distortion must
be fairly severe (around 10%) to be noted by an
untrained observer.

16. DISTORTION ANALYZERS
 In addition, most testing situations require a better
quantitative measure of harmonic distortion.
Harmonic distortion can be quantitatively measured
very accurately with a harmonic distortion analyzer,
which is generally referred to simply as a distortion
analyzer.

17. DISTORTION ANALYZERS
 A block diagram for a fundamental-suppression
harmonic analyzer is shown in Fig. 1. When the
instrument is used. switch S, is set to the "set level"
position, the band pass filter is adjusted to the
fundamental frequency and the attenuator network
is adjusted to obtain a full-scale voltmeter reading.
Fig. 1 Block diagram of a distortion analyzer.

18. DISTORTION ANALYZERS
 Switch S, is then set to the "distortion" position, the
rejection f:1ter is turned to the fundamental
frequency, and the attenuator is adjusted for a
maximum reading on the voltmeter.

19. DISTORTION ANALYZERS
 The total harmonic distortion (THD). which is
frequently expressed as a percentage, is defined as
the ratio of the rms value of all the harmonics to the
rms value of the fundamental, or
l
fundamenta
harmonics
THD
2
)
(



20. DISTORTION ANALYZERS
 This defining equation is somewhat inconvenient
from the standpoint of measurement. An alternative
working equation expresses total harmonic
distortion as the ratio of the rms value of all the
harmonics to the rms value of the total signal
including distortion. That is,
2
2
2
)
(
)
(
)
(
harmonics
l
funsamenta
harmonics
THD





21. DISTORTION ANALYZERS
 On the basis of the assumption that any distortion
caused by the components within the analyzer itself
or by the oscillator signal are small enough to be
neglected. Eq. 2 can be expressed as
where
THD = the total harmonic distortion
Ef = the amplitude of the fundamental frequency including the
harmonics
E2E3En = the amplitude of the individual harmonics
THD = E(harmonics) fundamental
f
n
E
THD
E
E
E
2
2
3
2
2
...




22. DISTORTION ANALYZERS
 EXAMPLE 1:
Compute the total harmonic distortion of a signal
that contains a fundamental signal with an rms
value of 10 V, a second harmonic with an rms value
of 3 V, a third harmonic with an rms value of 1.5 V,
and a fourth harmonic with an rms value of 0.6 V.

23. DISTORTION ANALYZERS
 SOLUTION:
Using Eq. 3, we compute the total harmonic distortion
as
10
6
.
0
5
.
1
3 2
2
2



THD
%
07
.
34
10
6
.
11



24. HARMONIC DISTORTION ANALYZERS
Fig.2a and Fig2b

25. HARMONIC DISTORTION ANALYZERS
 Fig2a is a harmonic distortion analyzer used to
measure THD.The signal source has very low
distortion and this can be checked by reading its
output distortion by connecting directly in to the
analyzer
 The signal from the source is fed in to the amplifier
under test.This generayes harmonics and the
original fundamental frequency.The fundamental
frequency is removed by the notch filter

26. HARMONIC DISTORTION ANALYZERS
 The switch SW is first placed in position 1 and the
total content of fundamental and harmonics is
measured.
 Then the switch is moved to position 2 to measure
just the harmonics . The value of THD is
THD= EH/ET*100

27. HARMONIC DISTORTION ANALYZERS
 Fig.2b shows an alternative arrangement, where
the values of Et and Eh are read simultaneously
and their ratio calculated and displayed as THD on
the indicator.
 For good accuracy the notch filter must have
excellent rejection and high pass characteristics

28. Thank you