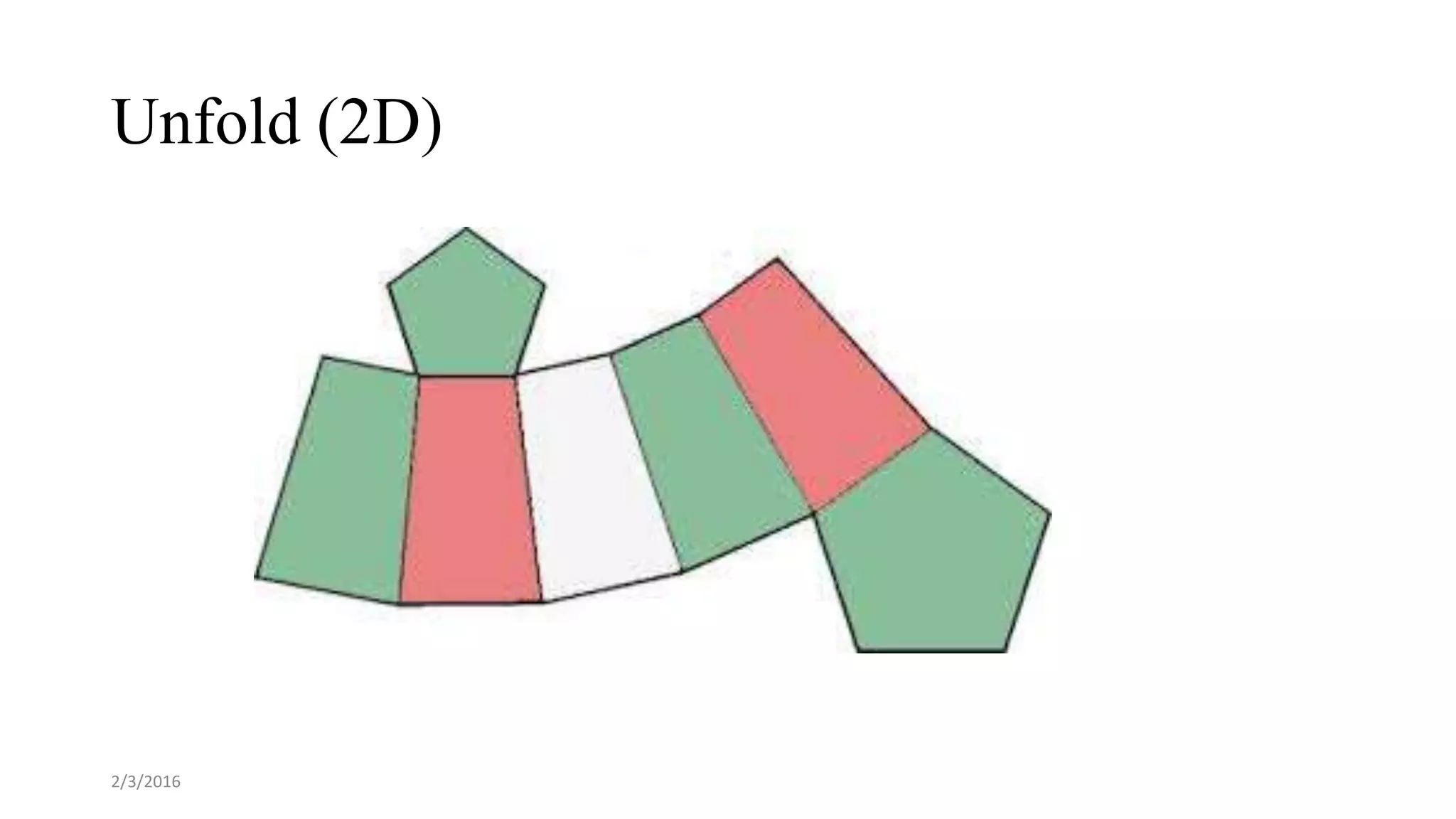
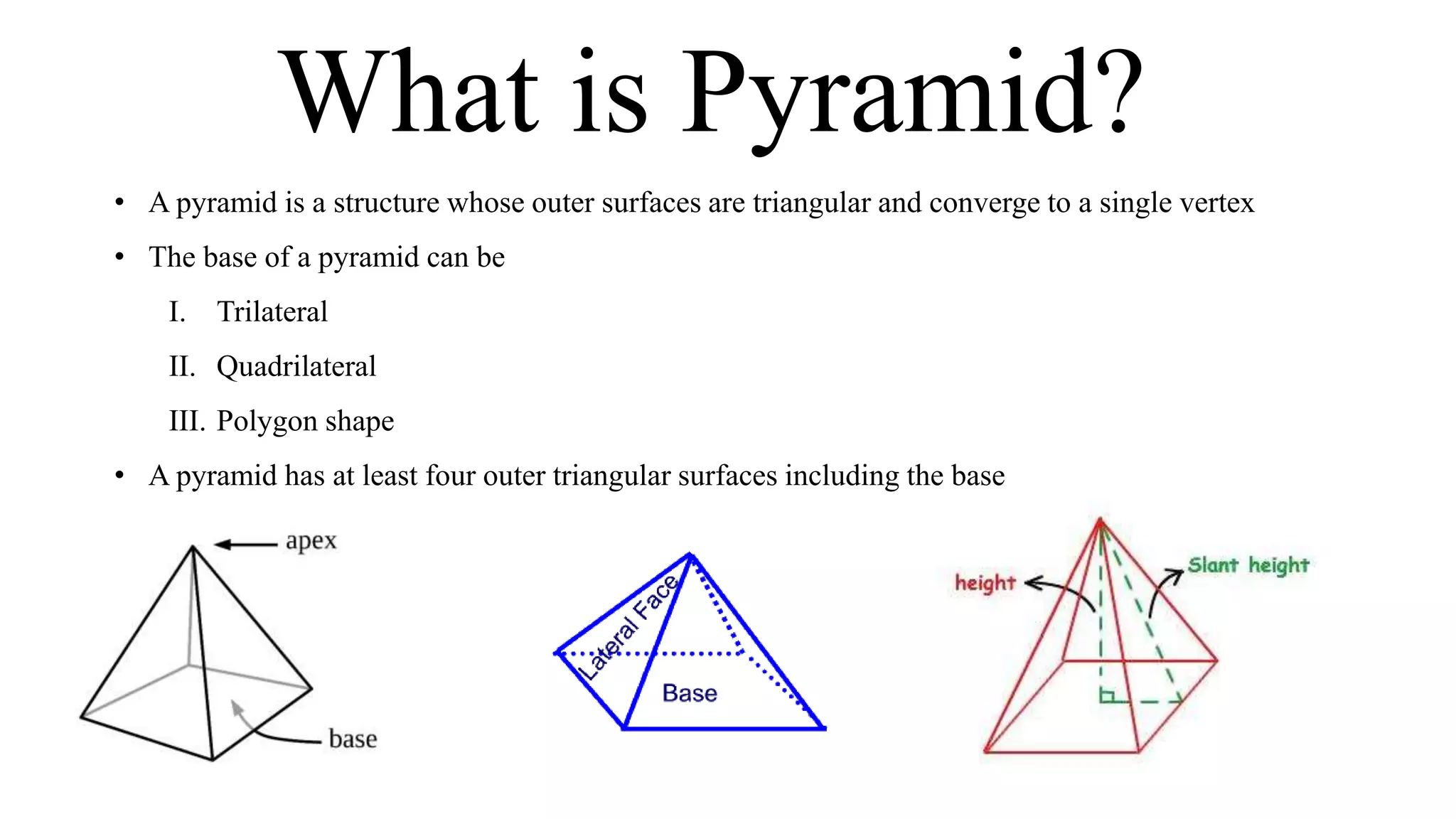
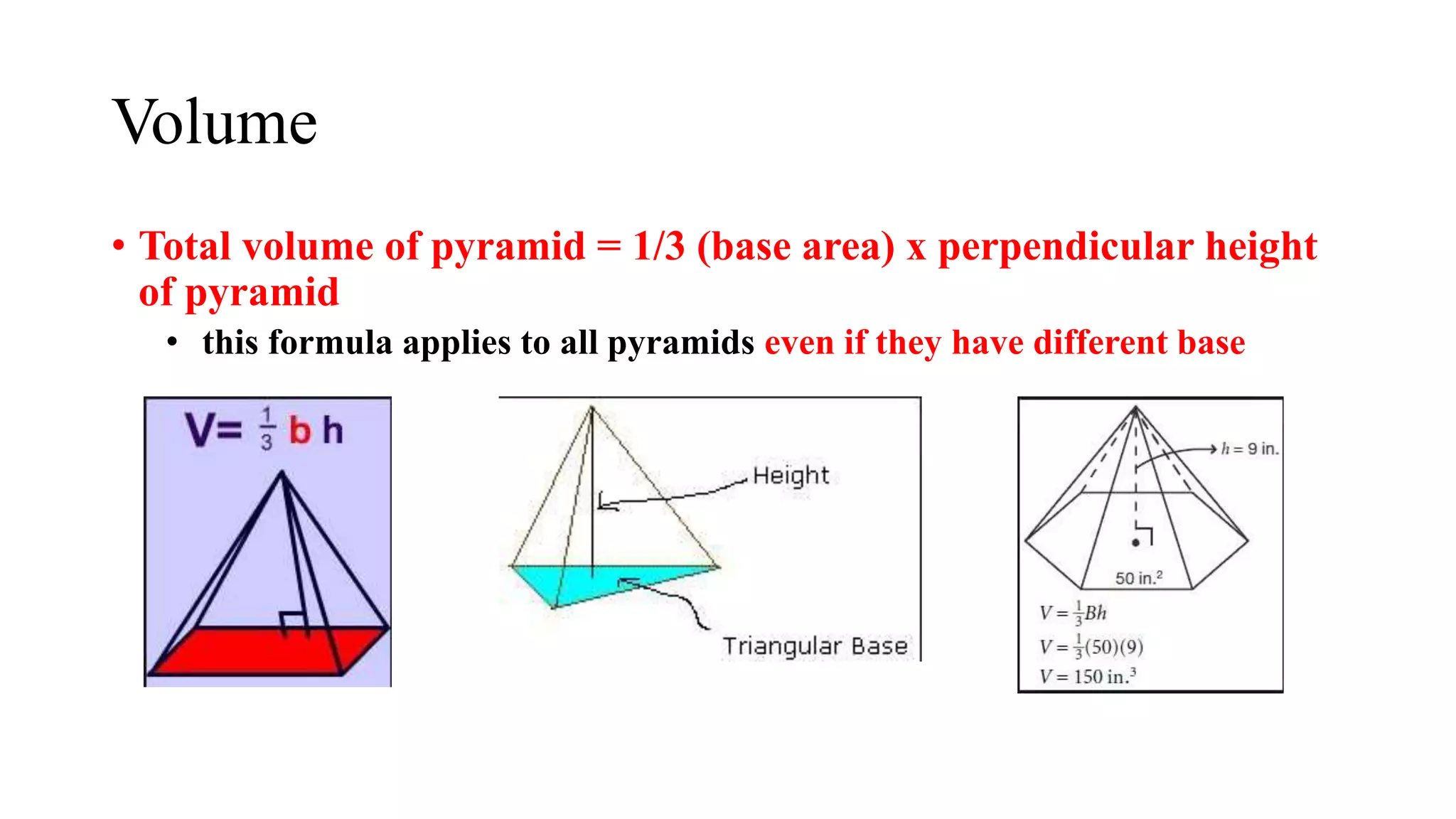
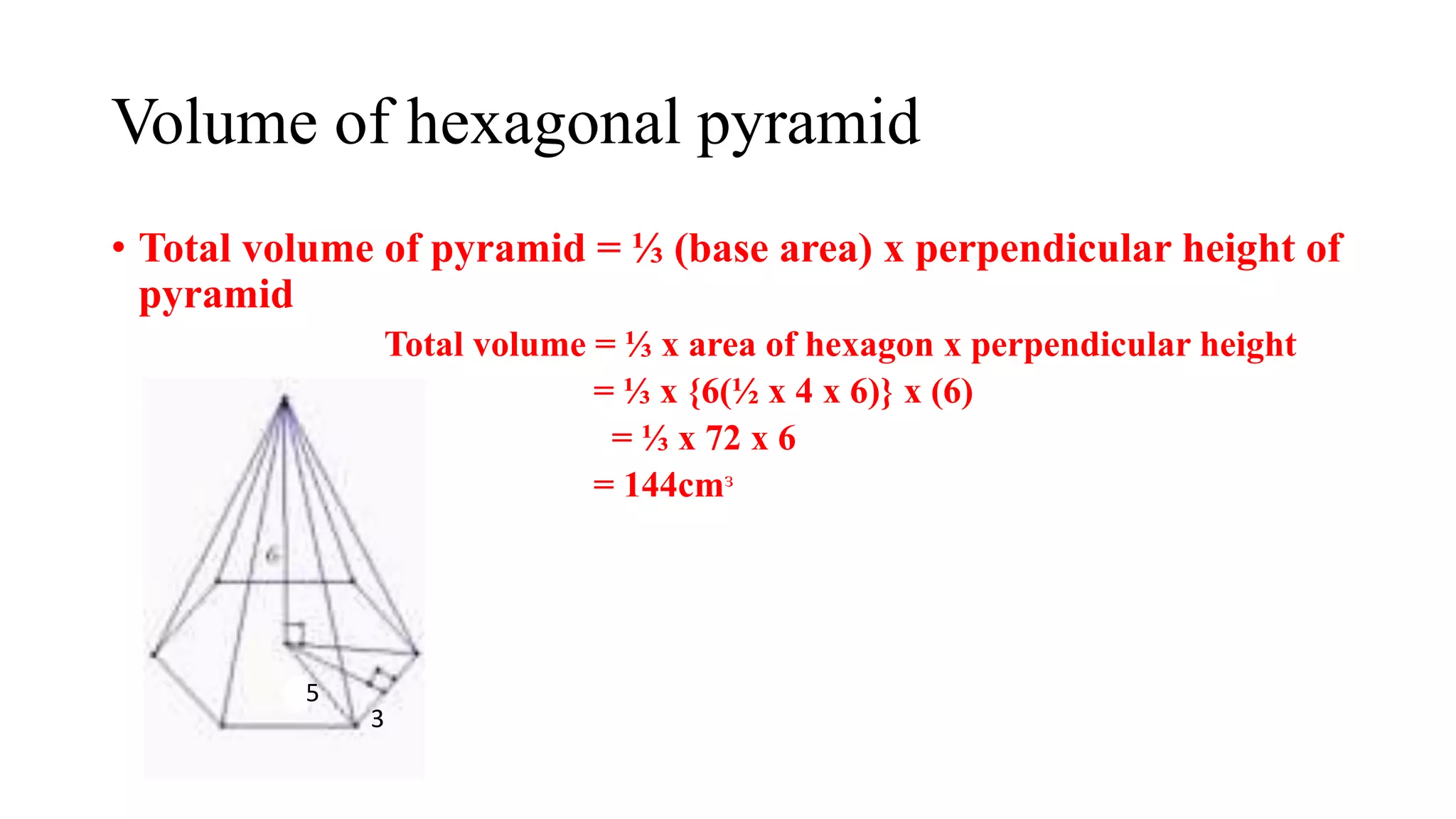
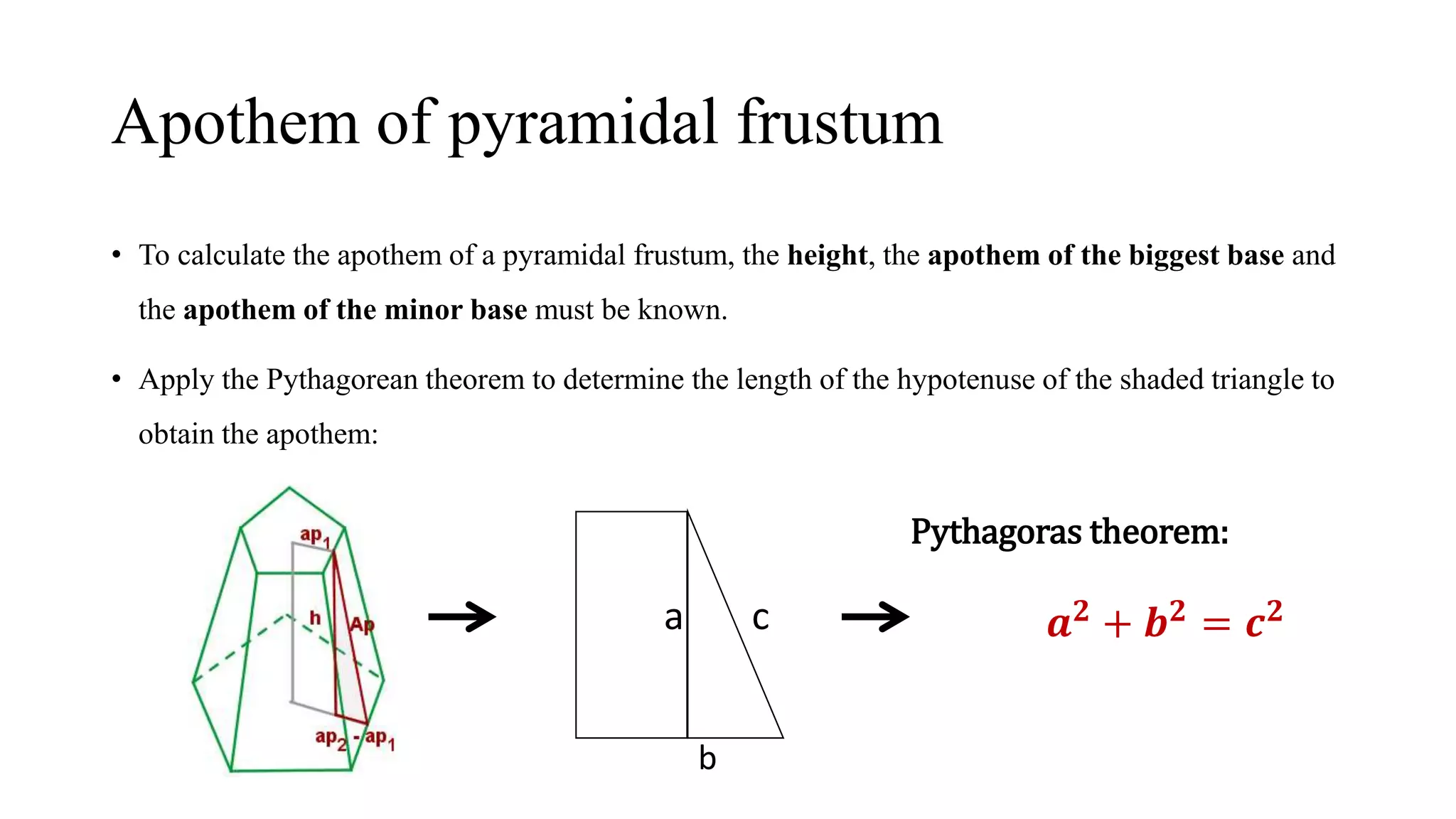
The document discusses pyramids and frustums. It defines a frustum as the part of a pyramid cut off by a plane parallel to the base. It provides formulas to calculate the surface area and volume of pyramids and frustums using measurements like the height, base areas, and apothem. Examples are given to demonstrate calculating surface areas and volumes of different pyramid and frustum shapes using the appropriate formulas.

1. Pyramid&Frustum

2. Introduction
The frustum of a pyramid or truncated pyramid is the result of cutting
a pyramid by a plane parallel to the base and separating the part
containing the apex.

3. *The lateral faces of a pyramidal frustum are trapezoids.
*The height of the pyramidal frustum is the perpendicular distance
between the bases.
*The apothem is the height of any of its sides.
How does an UNFOLD frustum
pyramid look like?

4. 2/3/2016
Unfold (2D)

5. 2/3/2016
Used in 3D games
The pyramid is constructed so that it fits neatly within the
viewing screen and extends far enough to include all the
model.
The part of the pyramid from the screen to the extreme left
is called a frustum.
This is a pyramid with its top cut off. In computer graphics
the screen is called the viewport. Everything within the
frustrum will get projected onto the viewport to create an
perspective image on your screen.

6. Pyramid and Frustum
• What is Pyramid?
• Types of Pyramid
• What is the different between Right Pyramid & Oblique Pyramid?
• Total Surface Area
• Volume
• Frustum of Pyramid

7. What is Pyramid?
• A pyramid is a structure whose outer surfaces are triangular and converge to a single vertex
• The base of a pyramid can be
I. Trilateral
II. Quadrilateral
III. Polygon shape
• A pyramid has at least four outer triangular surfaces including the base

8. Types of Pyramid
Pyramid Base Description
Regular Pyramid The base of a regular
pyramid is a regular
polygon and its faces are
equally sized triangles
Irregular Pyramid The base of an irregular
pyramid is an irregular
polygon, and as a result, its
faces are not equally sized

9. Right Pyramid A right pyramid has
isosceles triangles as its
faces and its apex lies
directly above the
midpoint of the base
Triangular Pyramid The base is a triangle
Oblique Pyramid An oblique pyramid does
not have all isosceles
triangles as its lateral sides

10. Pentagonal Pyramid The base is a pentagon
Hexagonal Pyramid The base is a hexagon

11. Right pyramid VS Oblique
pyramid
• If the apex is directly above the center of the base, then it is a Right Pyramid.
• If it is not directly above the center of the base, then it is a Oblique Pyramid.
Right Pyramid Oblique Pyramid

12. Total Surface Area
• Total surface area of pyramid = area of base + area of each of the
……………………………………………… lateral faces
Calculate the surface area of the following pyramid.
Total surface area = Area of base + Area of four lateral faces
= (6×6) + (1/2 × 6 × 12 ×4)
= 36 + 144
= 180 cm2

13. Calculate the surface area of the following pyramid.
Total surface area = Area of base + Area of four lateral faces
= (10×10) + (1/2 × 10 × 13 ×4)
= 100 + 260
= 360 cm2

14. Volume
• Total volume of pyramid = 1/3 (base area) x perpendicular height
of pyramid
• this formula applies to all pyramids even if they have different base

15. Volume of square base pyramid
• Total volume of pyramid = 1/3 (base area) x perpendicular
height of pyramid
Total volume of pyramid = 1/3 (10x10)(18)
= 600cmᵌ

16. Volume of triangular pyramid
• Total volume of pyramid = ⅓ (base area) x perpendicular
height of pyramid
Total volume = ⅓ x {½ x (14 x 8)} x (17)
=317 ⅓ cmᵌ

17. Volume of hexagonal pyramid
• 1st need to find the area of the hexagon

18. Volume of hexagonal pyramid
• Total volume of pyramid = ⅓ (base area) x perpendicular height of
pyramid
Total volume = ⅓ x area of hexagon x perpendicular height
= ⅓ x {6(½ x 4 x 6)} x (6)
= ⅓ x 72 x 6
= 144cmᵌ
3
5

19. Apothem of pyramidal frustum
• To calculate the apothem of a pyramidal frustum, the height, the apothem of the biggest base and
the apothem of the minor base must be known.
• Apply the Pythagorean theorem to determine the length of the hypotenuse of the shaded triangle to
obtain the apothem:
a c
b
Pythagoras theorem:
𝒂 𝟐 + 𝒃 𝟐 = 𝒄 𝟐

20. AL = Area of every side of pyramid
=
𝑃+𝑃`
2
x AP
Ar = Total surface area of frustum pyramid
=
𝑃+𝑃`
2
x AP + A +A’
Area of pyramidal frustum
P = Perimeter of the larger base
P’ = Perimeter of smaller base
A = Area of the larger base
A’ = Area of the smaller base
AP = Apothem of the truncated pyramid

21. Example:
Calculate the lateral area, surface area and volume of the truncated square pyramid whose larger base
edge is 24, smaller base edge is 14 cm and whose lateral edge is 13 cm.
P = 24 x 4
= 96cm
P’ = 14 x 4
= 56cm
A = 24 x 24
= 576cm²
A’ = 14 x 14
= 196cm²

22. Ar =
𝑃+𝑃`
2
x AP + A +A’
= 912 + 576 +196
= 1584cm²
AL =
𝑃+𝑃`
2
x AP
=
96+59
2
x 12
= 912cm²
𝑎2 = 𝑏2 + 𝑐2
ℎ2
= 52
+ 132
h = 12cm

23. Volume of a Frustum Pyramid
To calculate the volume of a frustum pyramid, 3 main factors
must be known; the height, the area of the top and bottom parts of the
frustum pyramid.
Without these factors, it is impossible to identify the volume of
the frustum pyramid without including external factors and formulas
into the mix.

24. Volume of a frustum pyramid
Main formula that is used to calculate the volume of a frustum
pyramid :
Height : h
Area of bases : B1 & B2
V1 =
1
3
h(B1 + B2 + B1B2 )

25. Due to the fact that a frustum pyramid is another form of
pyramid with its top cut off, the formula for said frustum pyramid has
many similarities to the pyramid’s formula in calculating its volume:
The length and width is removed and replaced with the area’s of the
top and bottom parts of the frustum pyramid
V1 =
1
3
h(B1 + B2 + B1B2 )
V1 =
1
3
(height)(length)(width)

26. How is it used?
Scenario 1 : Every information is given.
Example 1 :
Find the volume of the frustum pyramid whose area of bases are 10 cm2, 12cm2 and height is 9cm.
B1: 10cm2
B2: 12cm2
H : 9cm
V1 =
1
3
(9)(10+12+ (10)(12))
V1 = 98.86cm3

27. How is it used?
Scenario 2 : Angle instead of height is given.
Example 1 :
Find the volume of the frustum pyramid.

28. Find them one by one
B1(area of top square) : 3ft x 3ft
: 9ft2
B2(area of bottom square) : 7ft x 7ft
: 49ft2
Height : tan 62o30 =
: h = (2)(tan 62o30)
: h = 3.842ft
h
2ft

29. B1 = 9ft2
B2 = 49ft2
H = 3.842ft
V1 =
1
3
(3.842)(9+ 49+ (9)(49))
V1 =101.17 ft3