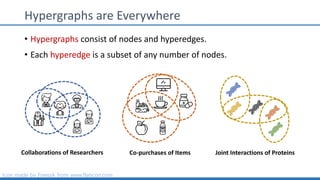
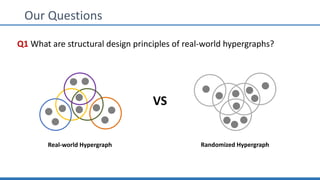
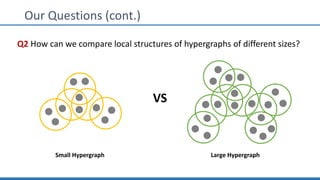
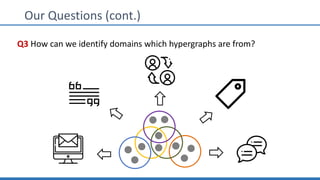
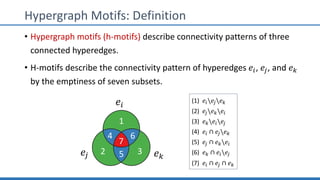
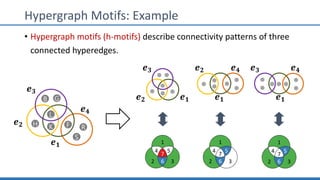
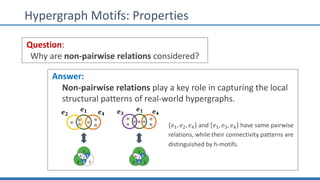
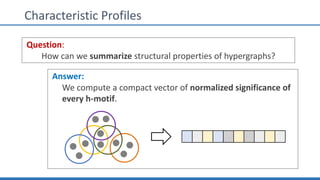
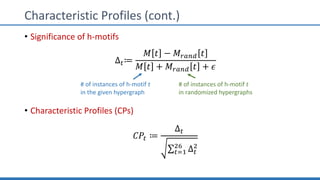
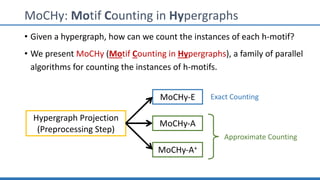
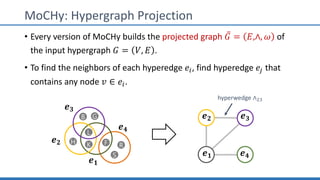
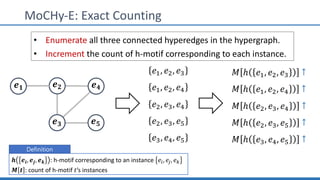
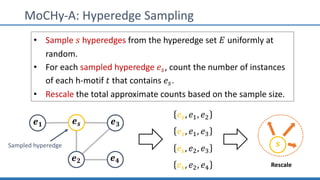
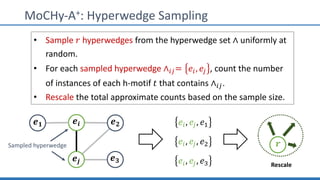
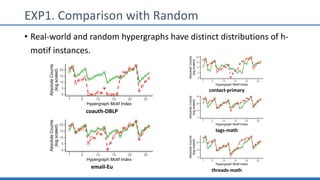
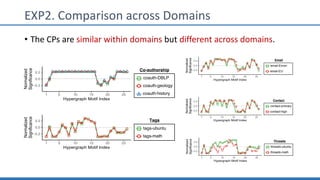
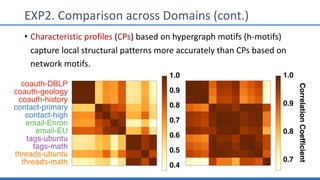
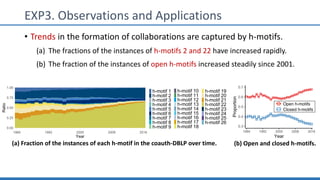
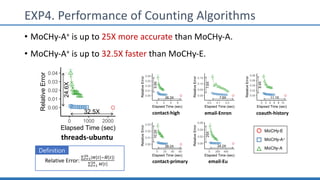
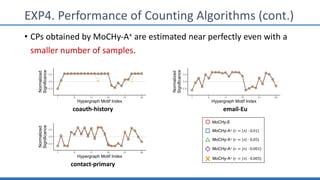
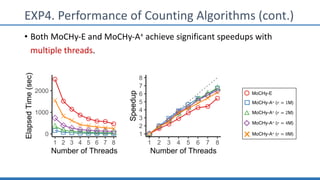
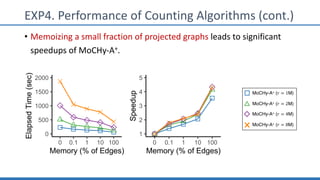
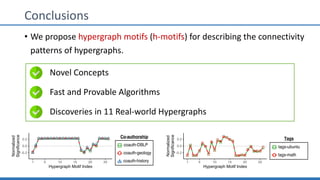
The document discusses hypergraph motifs, which describe connectivity patterns between three connected hyperedges in a hypergraph. It proposes MoCHy, a family of parallel algorithms for counting instances of hypergraph motifs in large hypergraphs. Experimental results on real-world hypergraphs from different domains show that their motif distributions differ significantly from randomized hypergraphs, and MoCHy can efficiently count motifs in large hypergraphs.