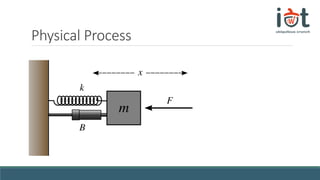
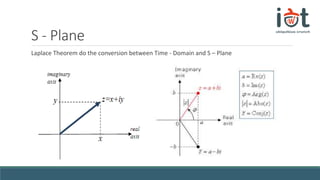
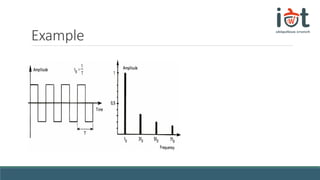
The document discusses transfer functions and their use in mathematical modeling of physical systems. It defines a transfer function as representing a system function in the frequency domain. An example differential equation for a physical system is given and the corresponding transfer function is derived by taking the Laplace transform. The transfer function is defined as the ratio of the output to input signals in the frequency domain. Convolution and the S-plane are also briefly introduced in relation to converting between the time and frequency domains.

1. Transfer Function
SUMMER SCHOOL

2. Physical Process

3. Mathematical Modeling
Using the Newton Laws, we have:
ma t + 𝑏𝑣(𝑡) + 𝑘𝑥(𝑡) = F(t)
Now, we know that:
𝑣(𝑡) =
ⅆ𝑥
ⅆ𝑡
= 𝑥(t) and 𝑎 𝑡 =
ⅆ2 𝑥
ⅆ𝑡2 = 𝑥(t)
Then we have:
𝑚 𝑥 𝑡 + 𝑏 𝑥 𝑡 + 𝑘𝑥 𝑡 = 𝐹 𝑡
Now we solve for x to see the evolution of the system in time

4. Convolution
It is a mathematical operation between two signals in order to get a third signal.

5. S - Plane
Laplace Theorem do the conversion between Time - Domain and S – Plane

6. Weight function vs Transfer Function
h(t) -> Weight Function (system function represented in Time - Domain)
H(s) -> Transfer Function (system function represented in Frequency - Domain)

7. Example

8. TF for our Physical System
Differential equation from our example:
𝑚 𝑥 𝑡 + 𝑏 𝑥 𝑡 + 𝑘𝑥 𝑡 = 𝐹 𝑡
After we apply Laplace Transform, becomes:
𝑚𝑠2 + 𝑏𝑠 + 𝑘 𝑋 𝑠 = 𝐹 𝑠
Thus we get:
𝐻 𝑠 =
𝑋(𝑠)
𝐹(𝑠)
=
1
𝑚𝑠2 + 𝑏𝑠 + 𝑘
Where
H(s) -> Transfer Function for our Physical System

9. Questions?