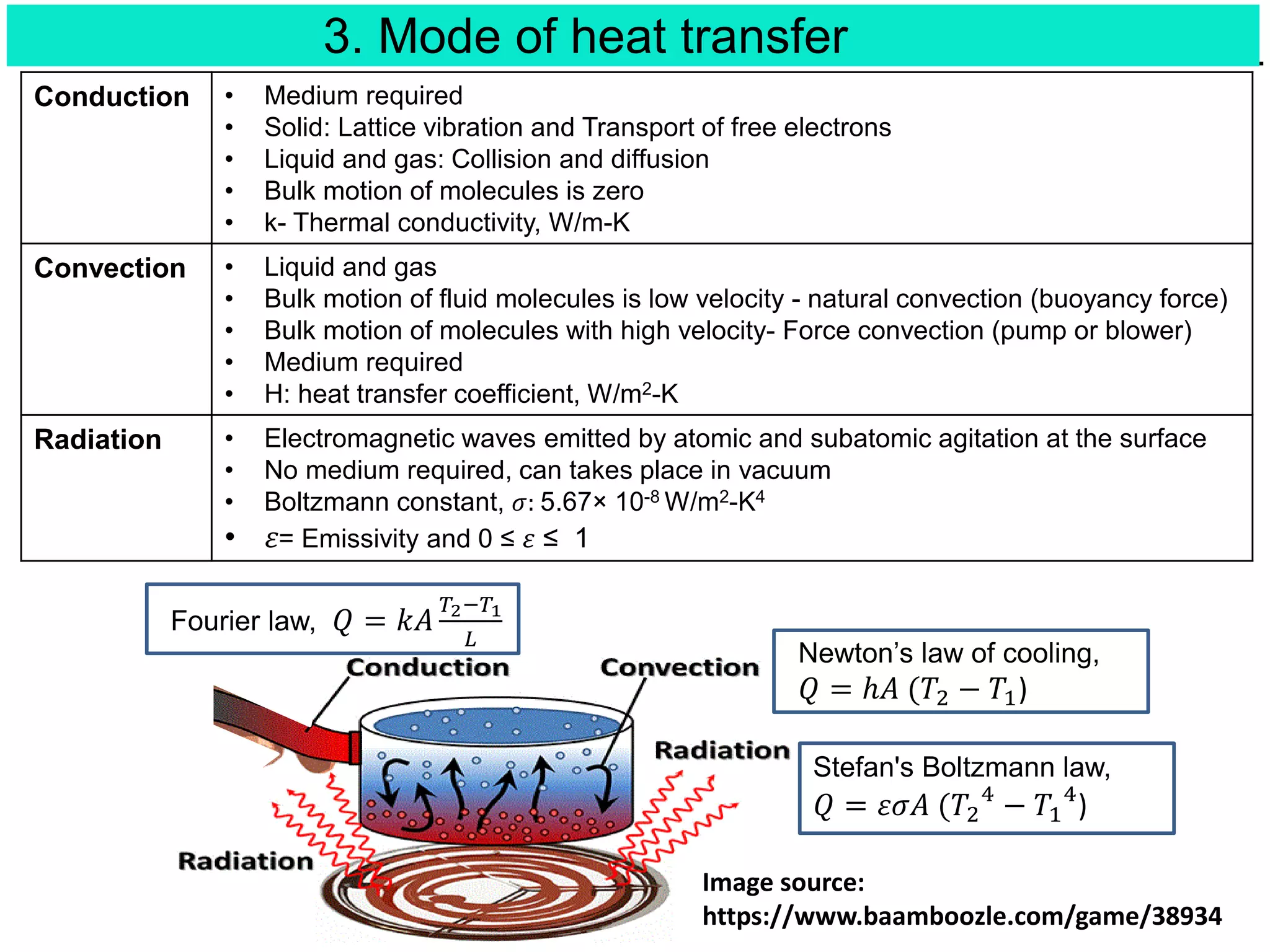
This document discusses heat transfer and thermodynamics. It begins by introducing concepts like temperature, heat, and work. It then covers the three laws of thermodynamics. The main modes of heat transfer are conduction, convection, and radiation. The document also derives the general heat conduction equation in Cartesian coordinates for a material with constant thermal conductivity. It shows how this equation can be simplified for different boundary conditions and whether heat generation is present or not.