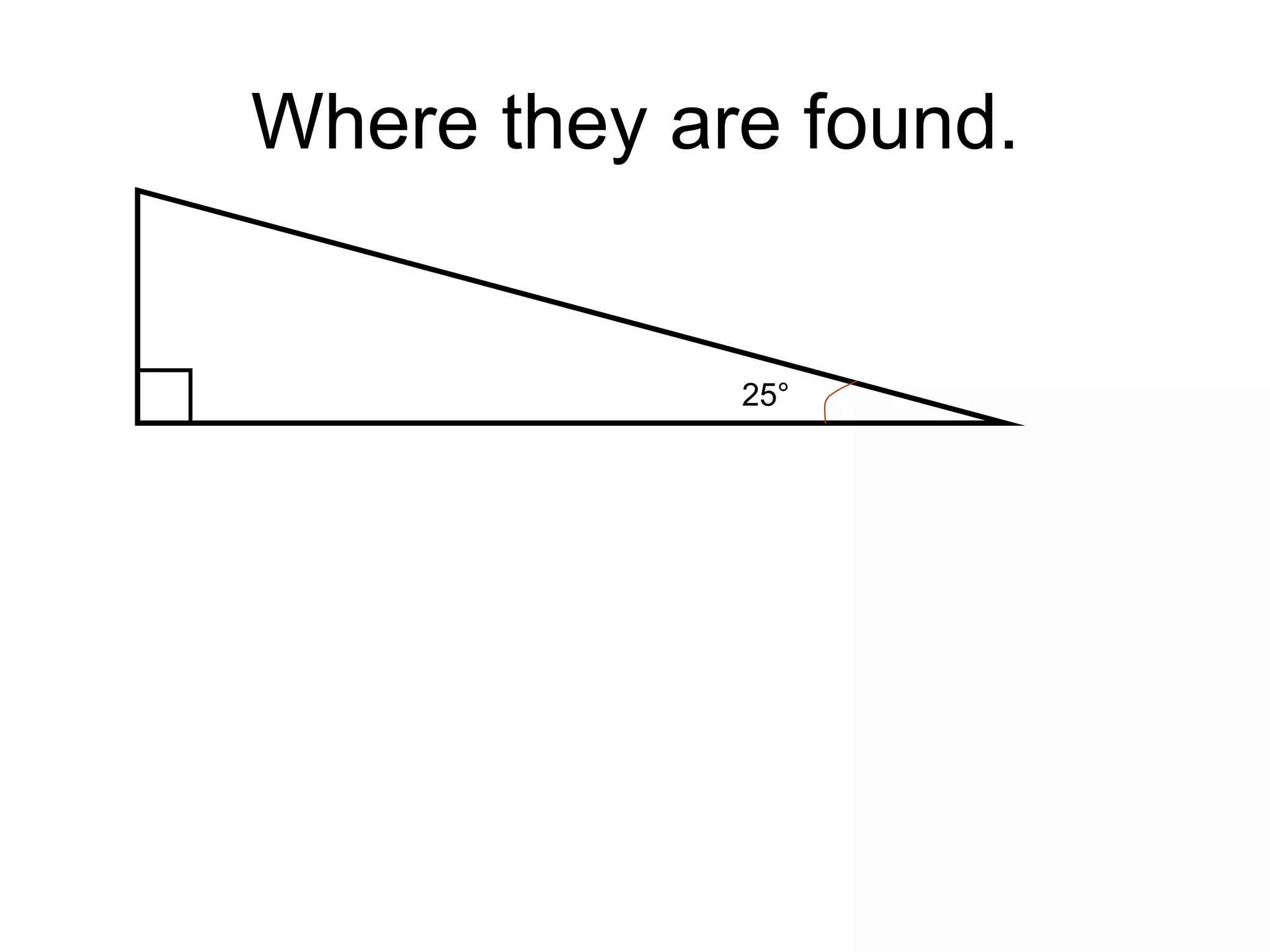
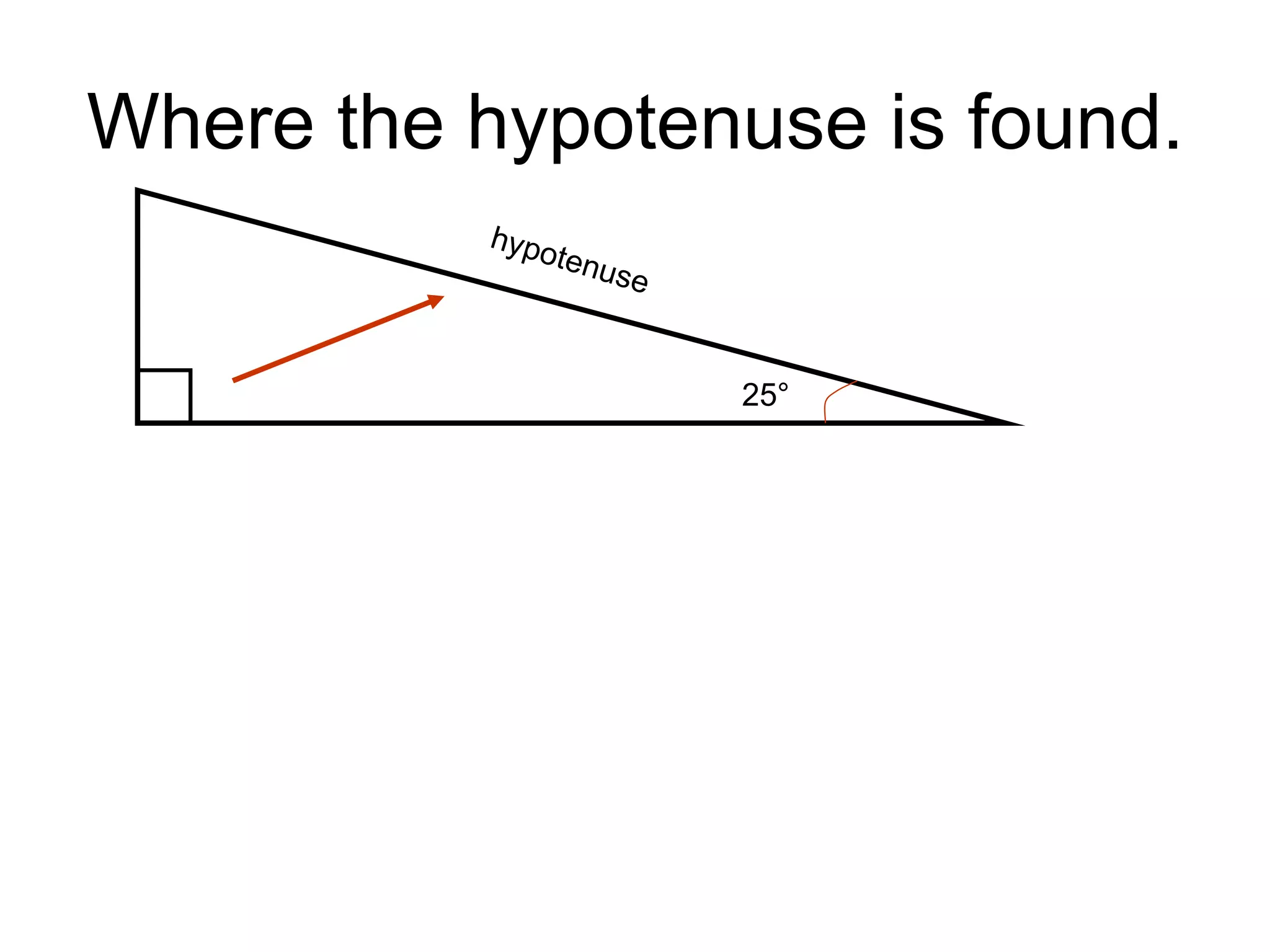
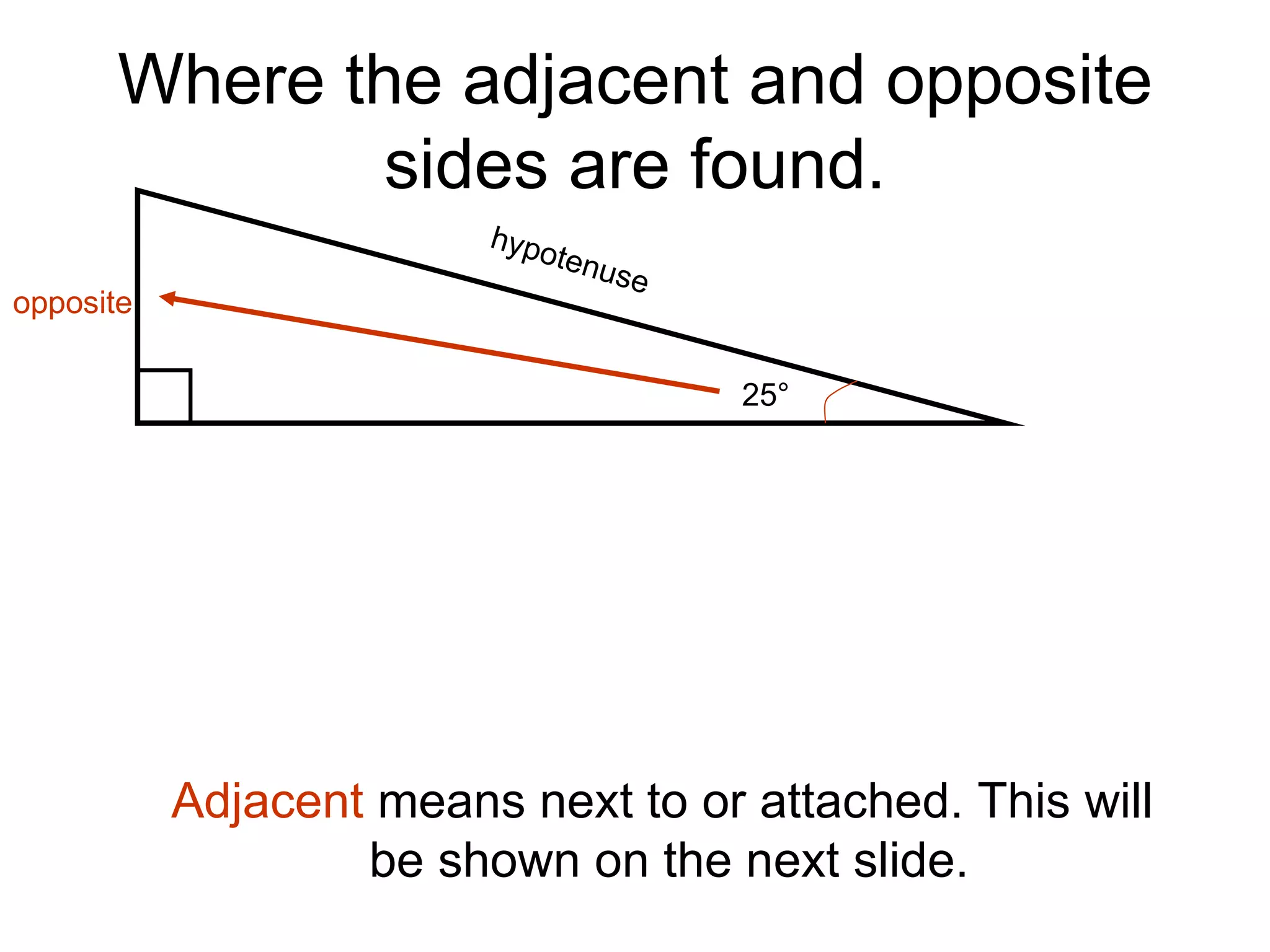
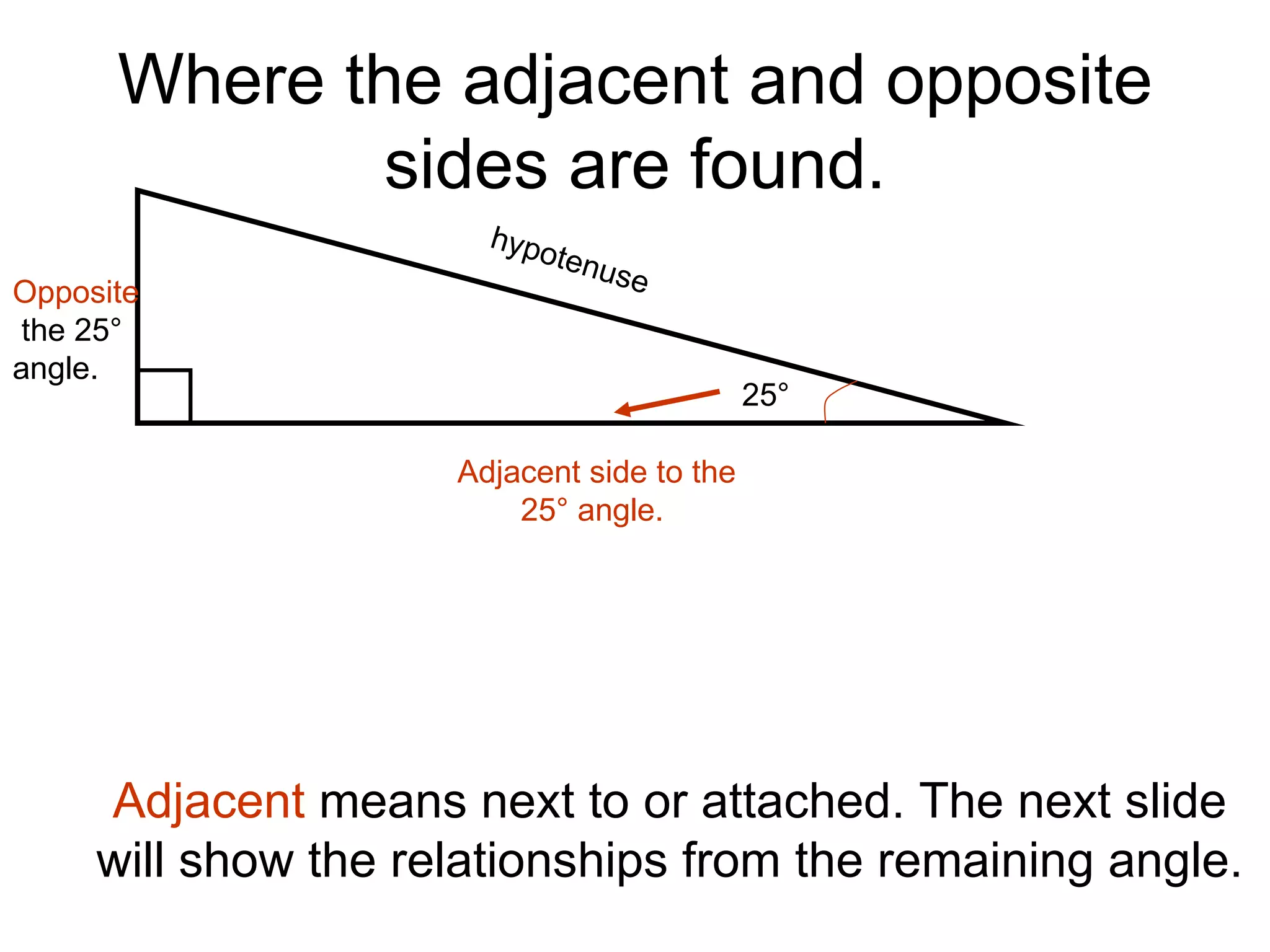
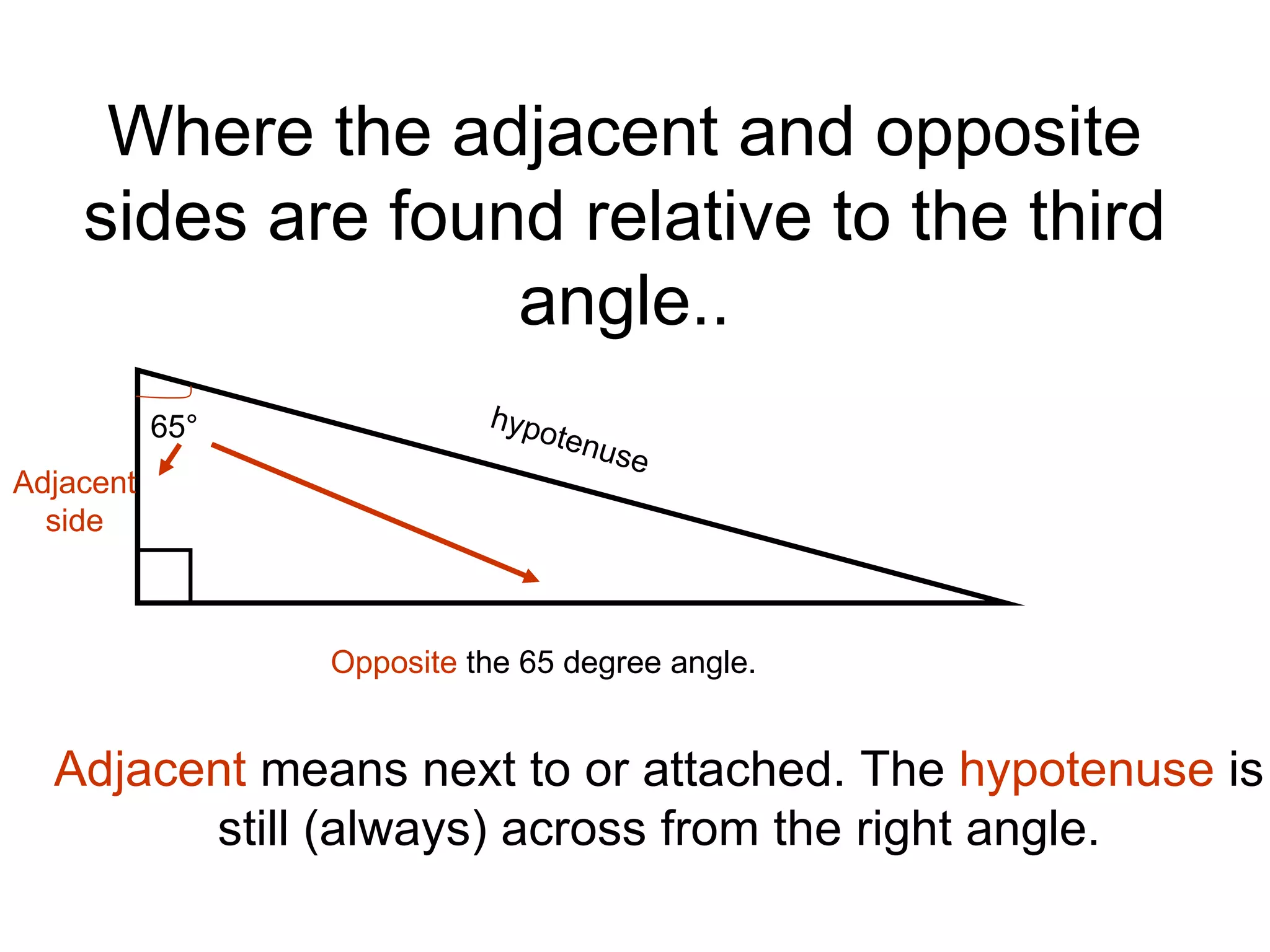
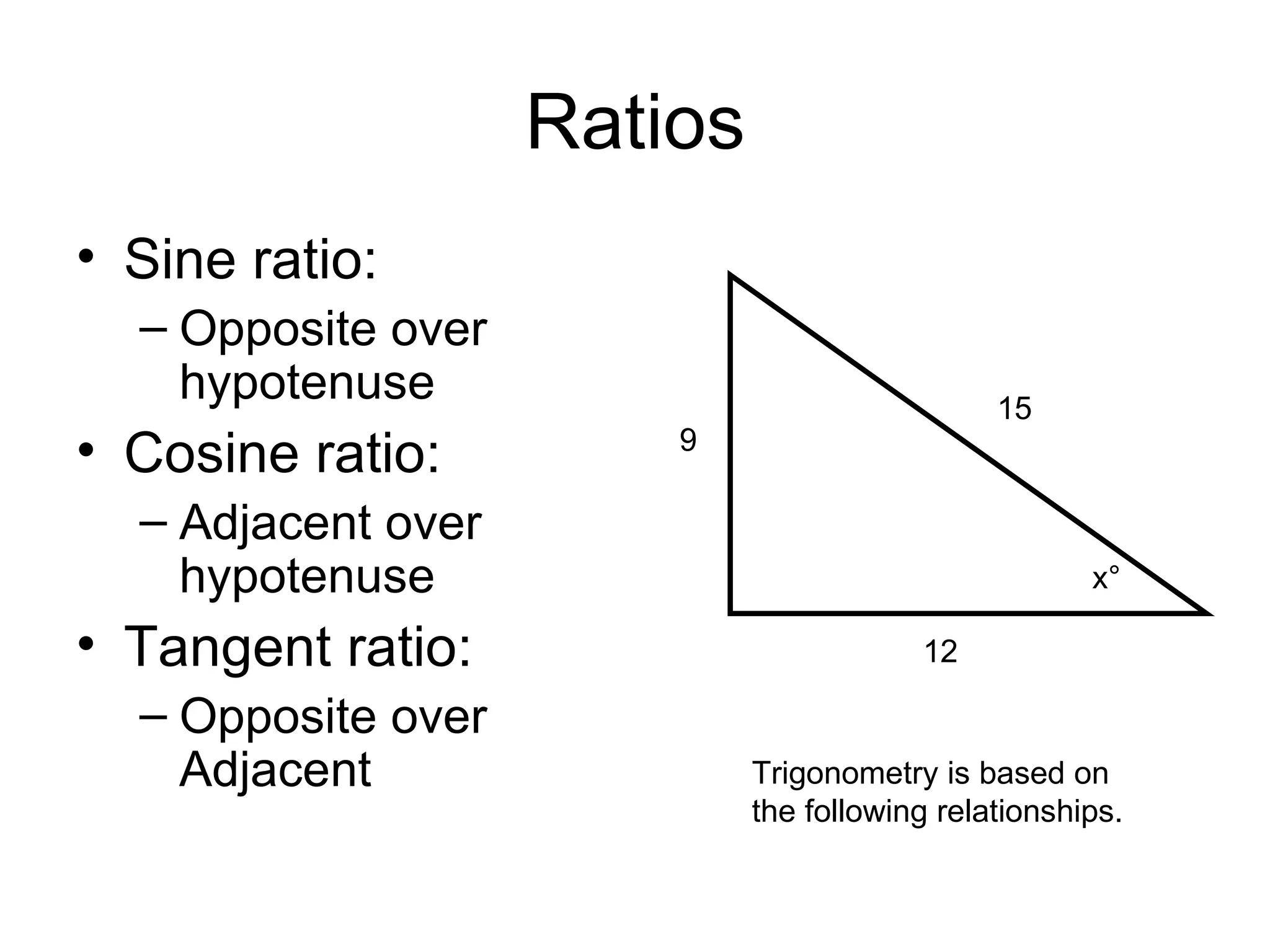
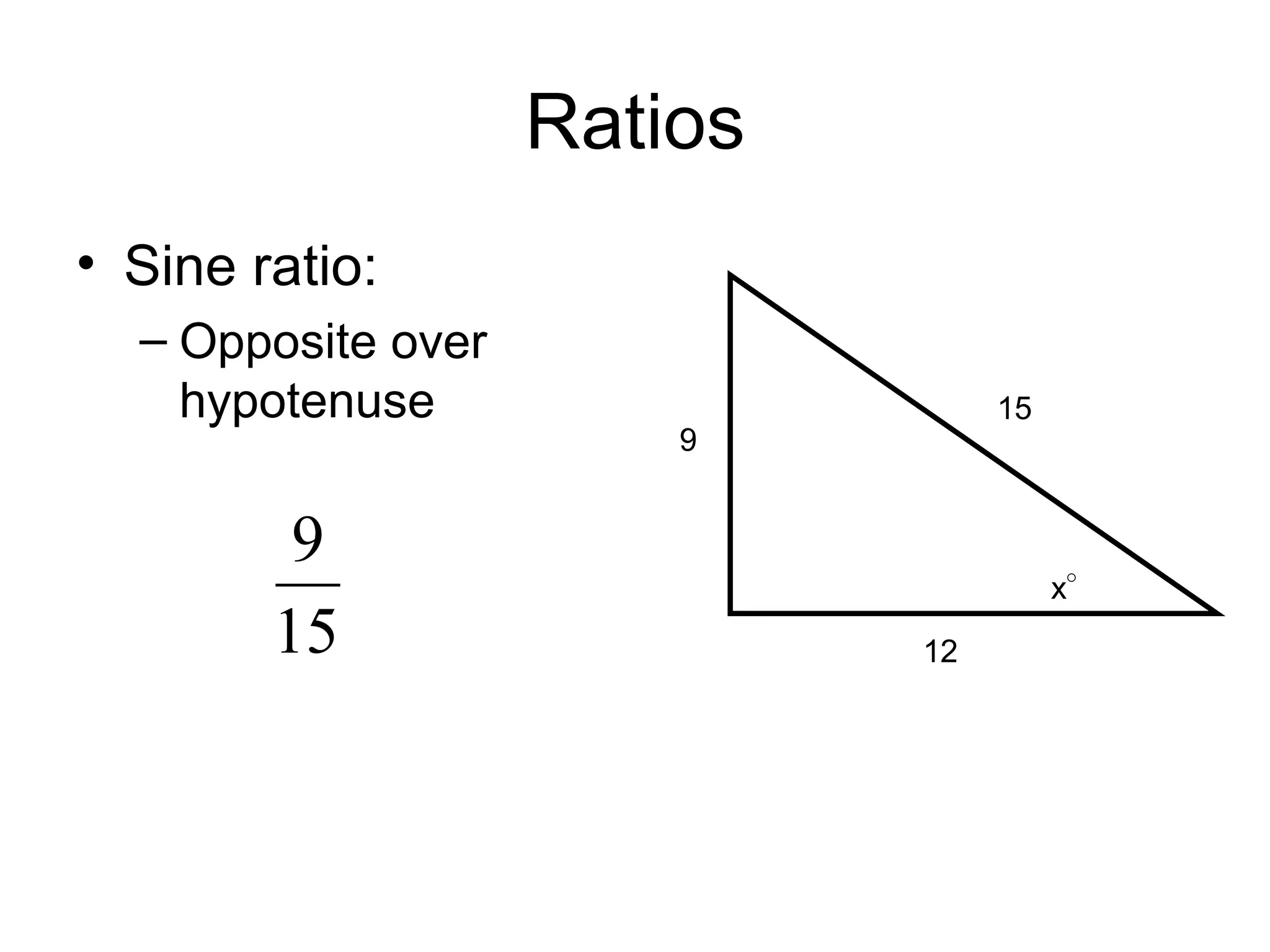
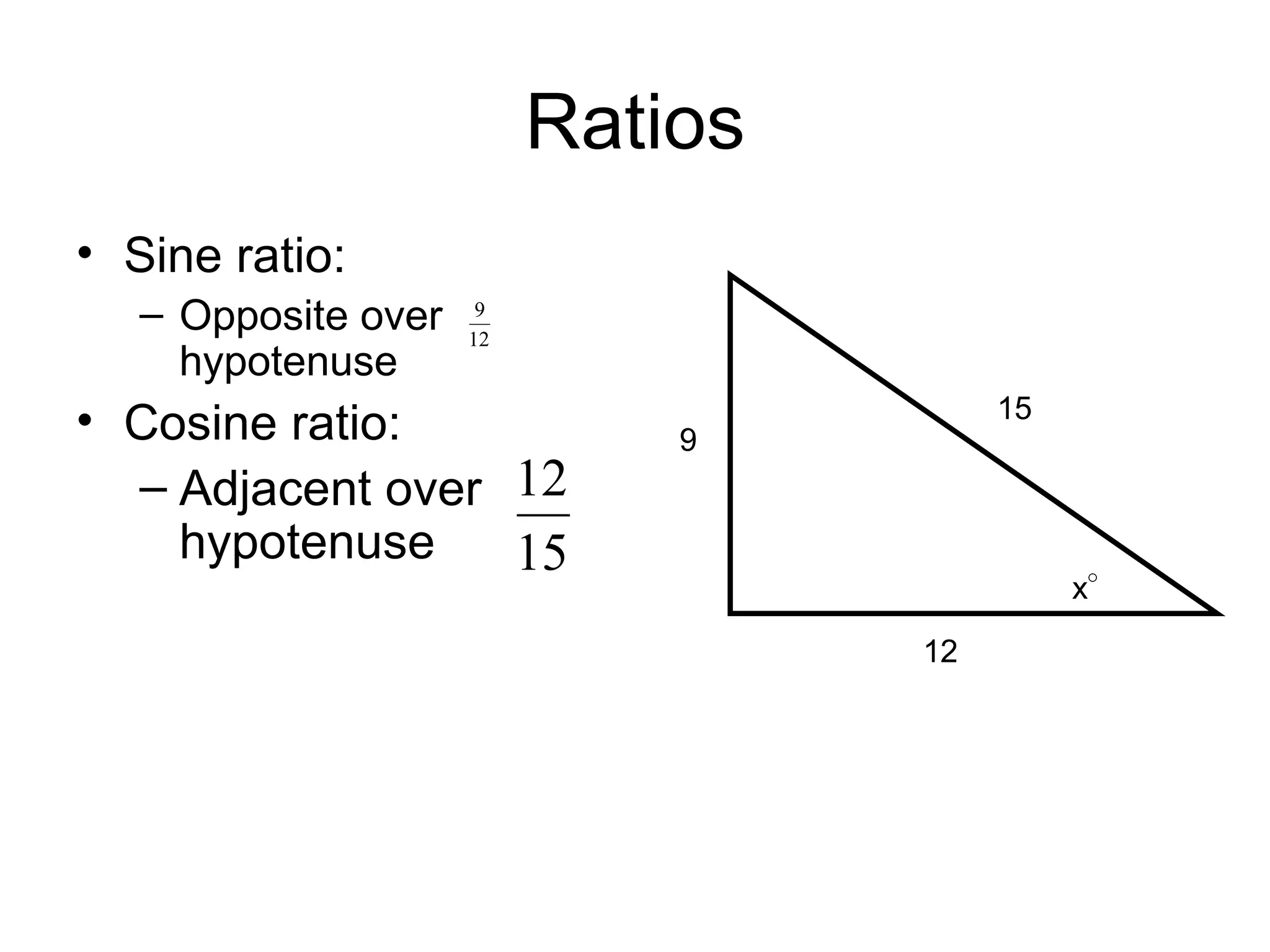
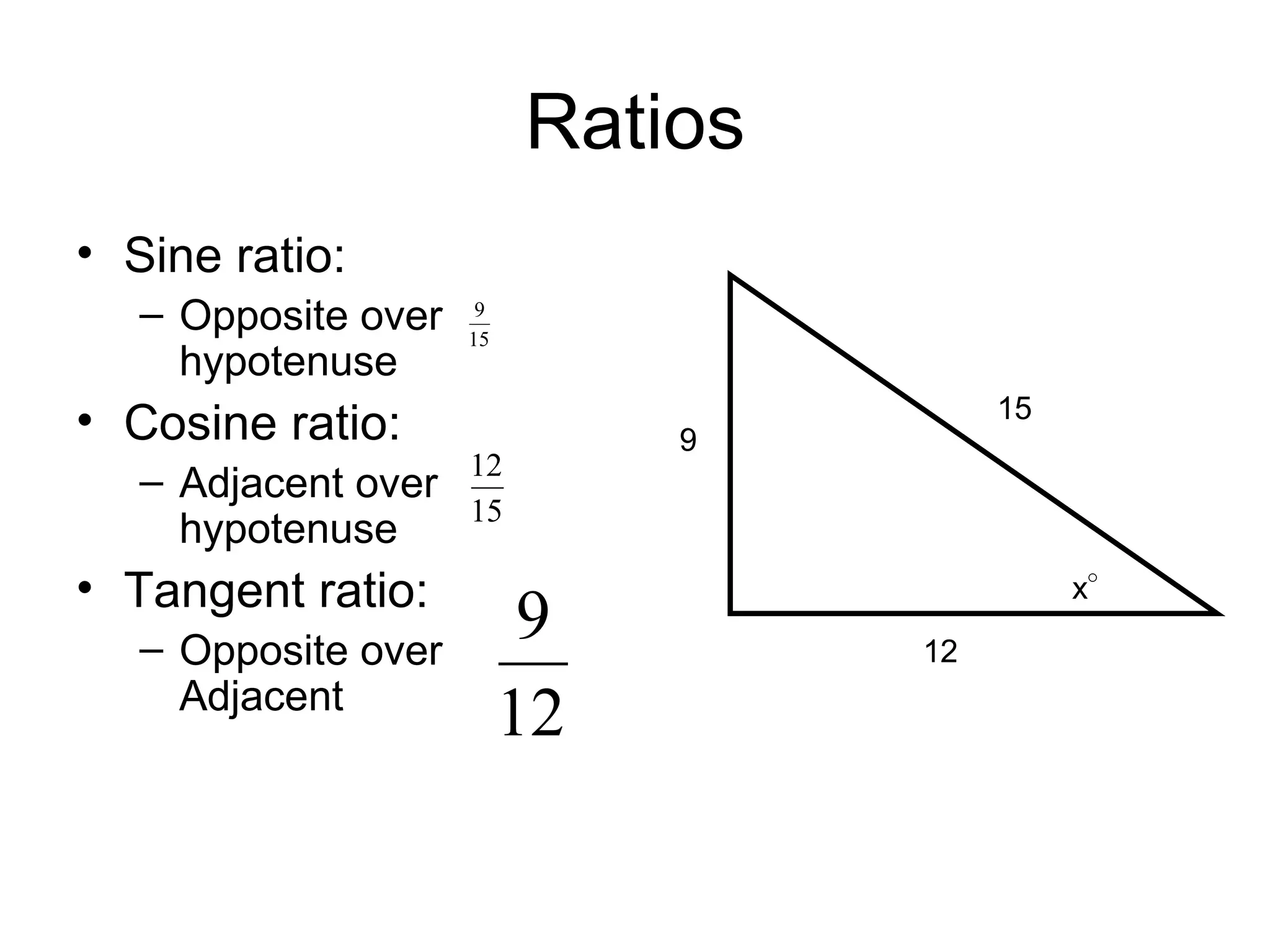
SOHCAHTOA was a wise Trigonometric Tribe chief who helped people solve problems using right triangles. He discovered the relationships between opposite, adjacent, and hypotenuse sides and angles, which are remembered through the mnemonic "SOHCAHTOA". The document then explains the definitions of opposite, adjacent, and hypotenuse sides relative to a given angle in a right triangle, and introduces the sine, cosine, and tangent ratios used in trigonometry.

1. Sine/Cosine/Tangent Focus: Find out who is sohacahtoa and why is the spelling of his name so important?

2. sohcahtoa SOHCAHTOA was the chief of the Trigonometric Tribe. He was a very wise man and people would go to him to solve their most pressing problems. Legend has it that he is the grandson of Sacajewea, for whom a famous park was erected in SW Washington state in time for Lewis and Clark to have a bath.

3. sohcahtoa SOHCAHTOA, a contemporary of Pythagorus, worked on finding ways to solve lengths and distances on right triangles. SOHCAHTOA is a famous dead mathematician, but his name lives on in legendary brilliance, he is still alive and working with roots. Spell his name correctly and you will certain pass into the tribe of Trigonometry’s lore.

4. Right Triangles’ Sides Hypotenuse Adjacent side Opposite side The adjacent and opposite sides are relative terms, compared to the location of the angle in question. The hypotenuse is always across from the right angle in a triangle.

5. Where they are found. 25°

6. Where the hypotenuse is found. hypotenuse 25°

7. Where the adjacent and opposite sides are found. hypotenuse 25° opposite Adjacent means next to or attached. This will be shown on the next slide.

8. Where the adjacent and opposite sides are found. hypotenuse 25° Adjacent side to the 25° angle. Adjacent means next to or attached. The next slide will show the relationships from the remaining angle. Opposite the 25° angle.

9. Where the adjacent and opposite sides are found relative to the third angle.. hypotenuse 65° Adjacent side Adjacent means next to or attached. The hypotenuse is still (always) across from the right angle. Opposite the 65 degree angle.

10. Ratios Sine ratio: Opposite over hypotenuse Cosine ratio: Adjacent over hypotenuse Tangent ratio: Opposite over Adjacent 9 12 15 Trigonometry is based on the following relationships. x°

11. Ratios Sine ratio: Opposite over hypotenuse 9 12 15 x °

12. Ratios Sine ratio: Opposite over hypotenuse Cosine ratio: Adjacent over hypotenuse 9 12 15 x °

13. Ratios Sine ratio: Opposite over hypotenuse Cosine ratio: Adjacent over hypotenuse Tangent ratio: Opposite over Adjacent 9 12 15 x °

14. Ratios Sine ratio: Opposite over hypotenuse Cosine ratio: Adjacent over hypotenuse Tangent ratio: Opposite over Adjacent 9 12 15 Trigonometry charts are usually found at the back of math textbooks. Is there one in your book on page 668? x ° We can use these fractions as division statements and compare the resulting answers to determine the angle’s measurement.

15. What is the missing angle measurement?