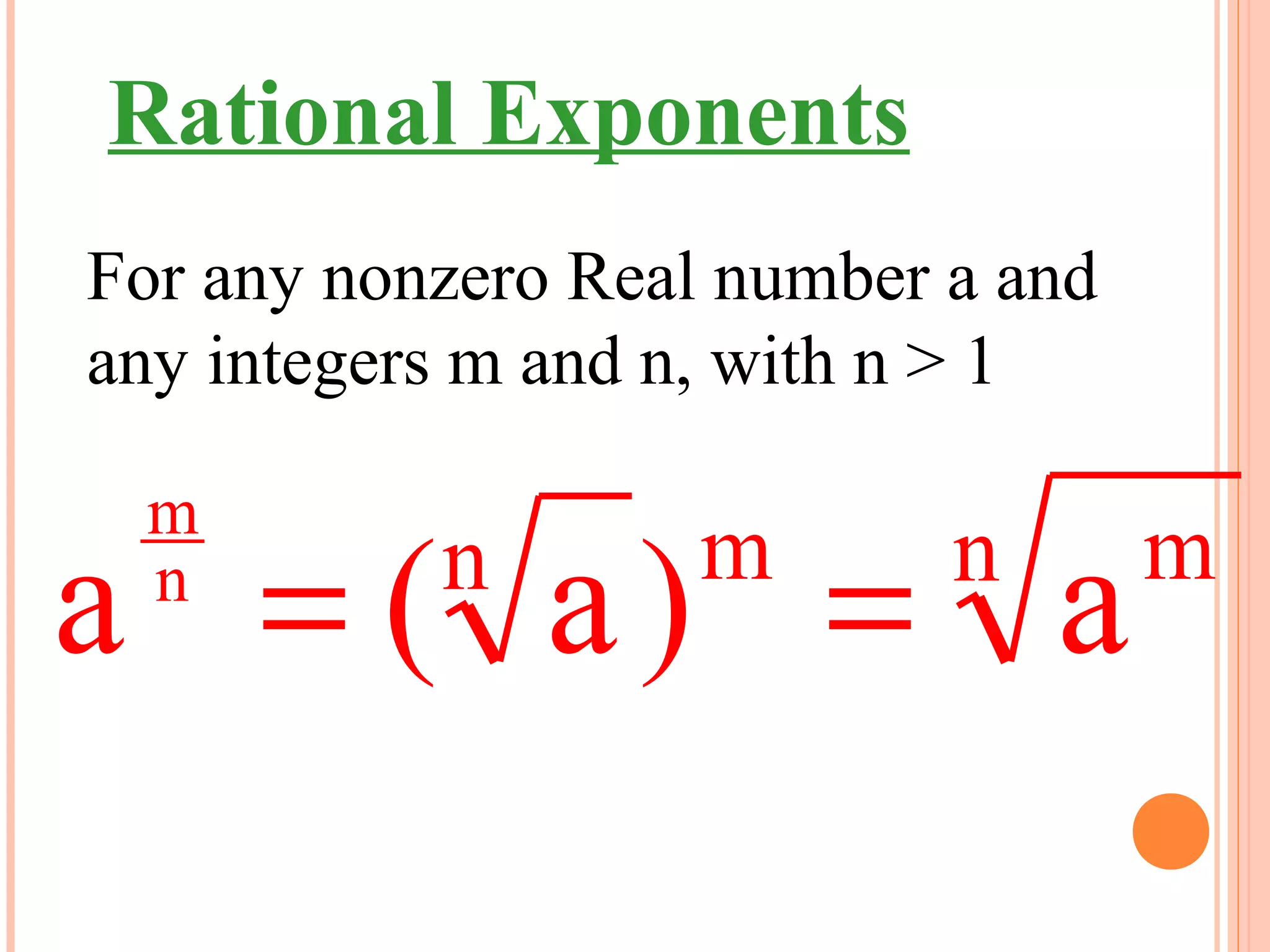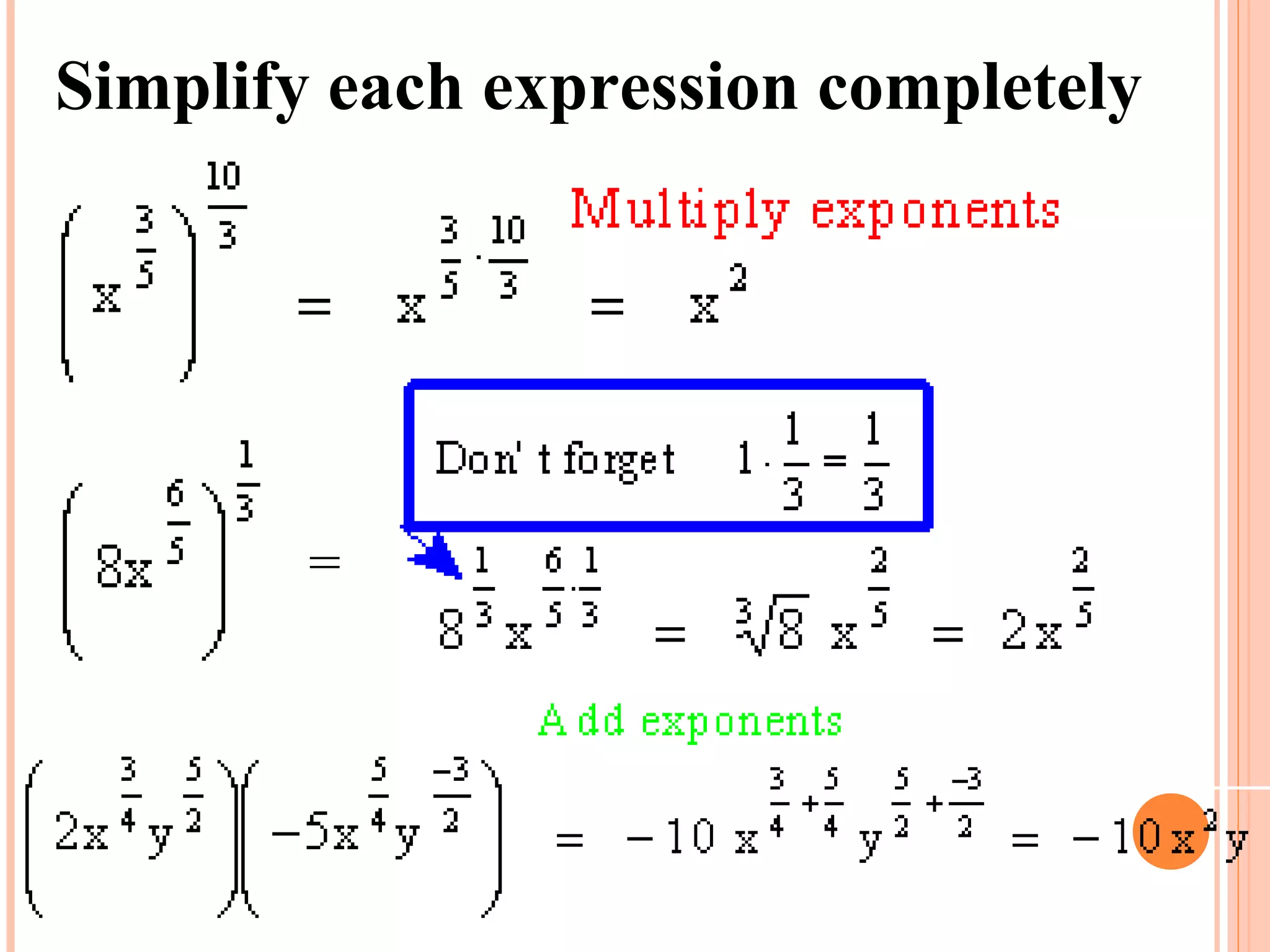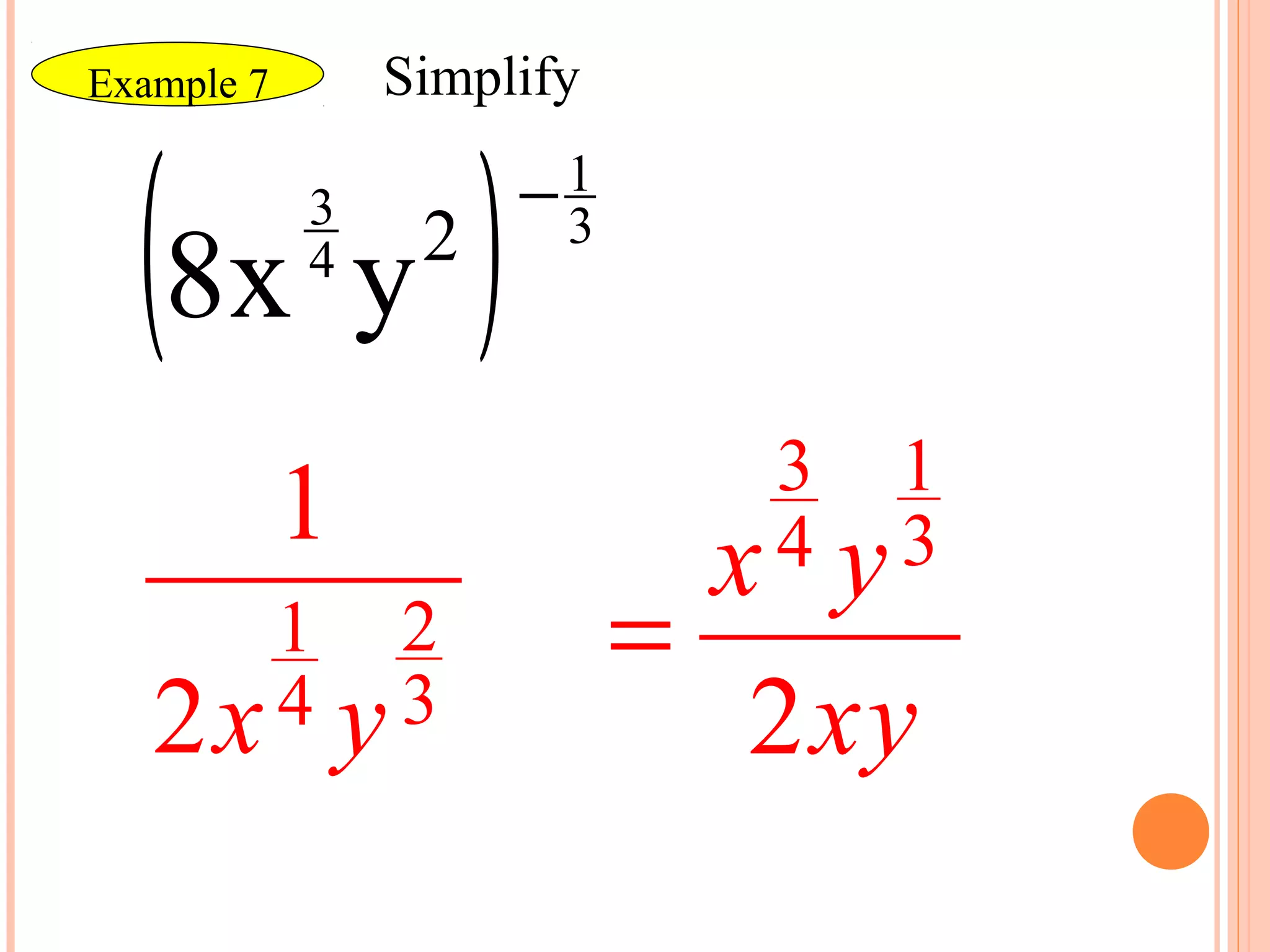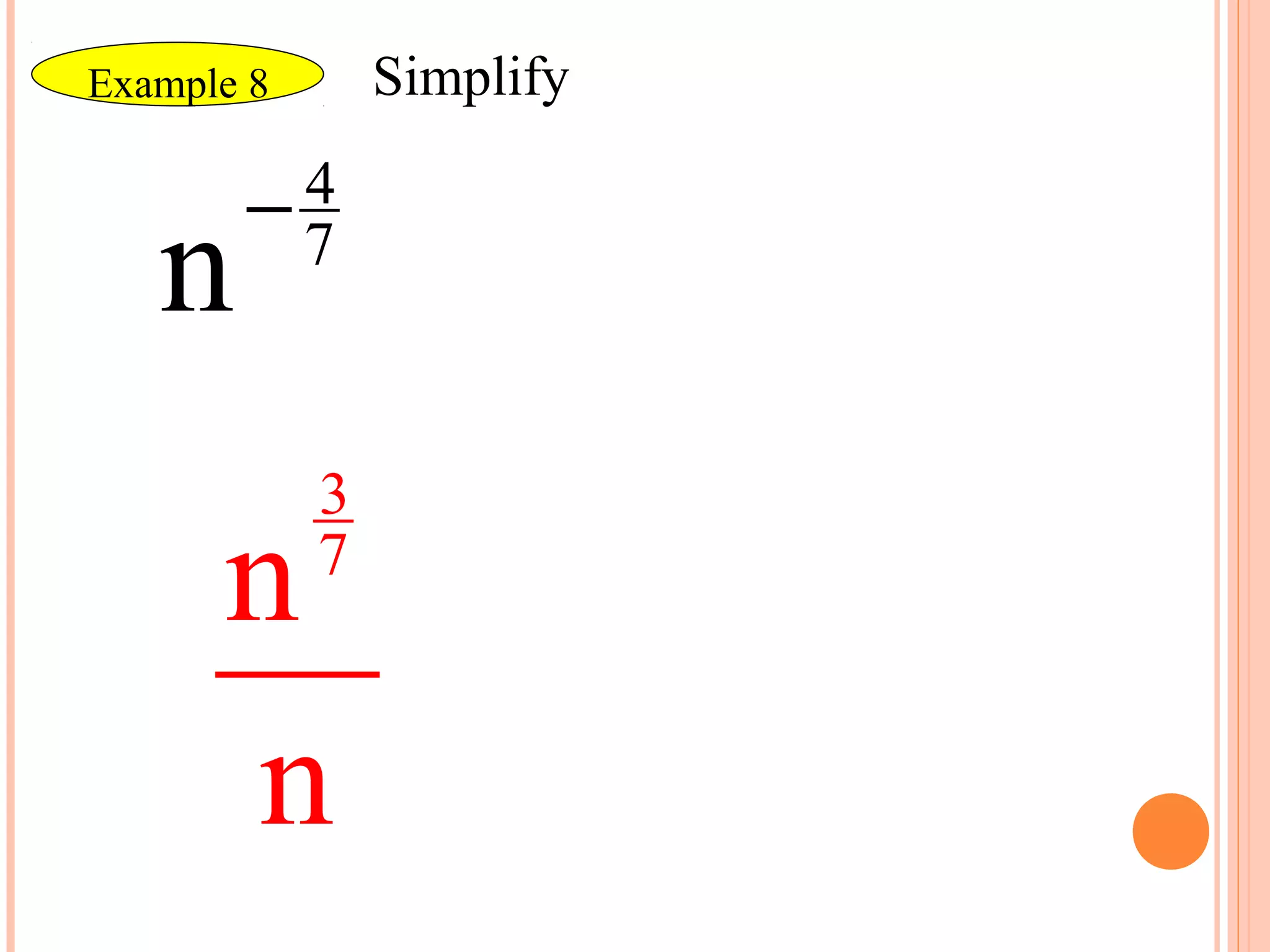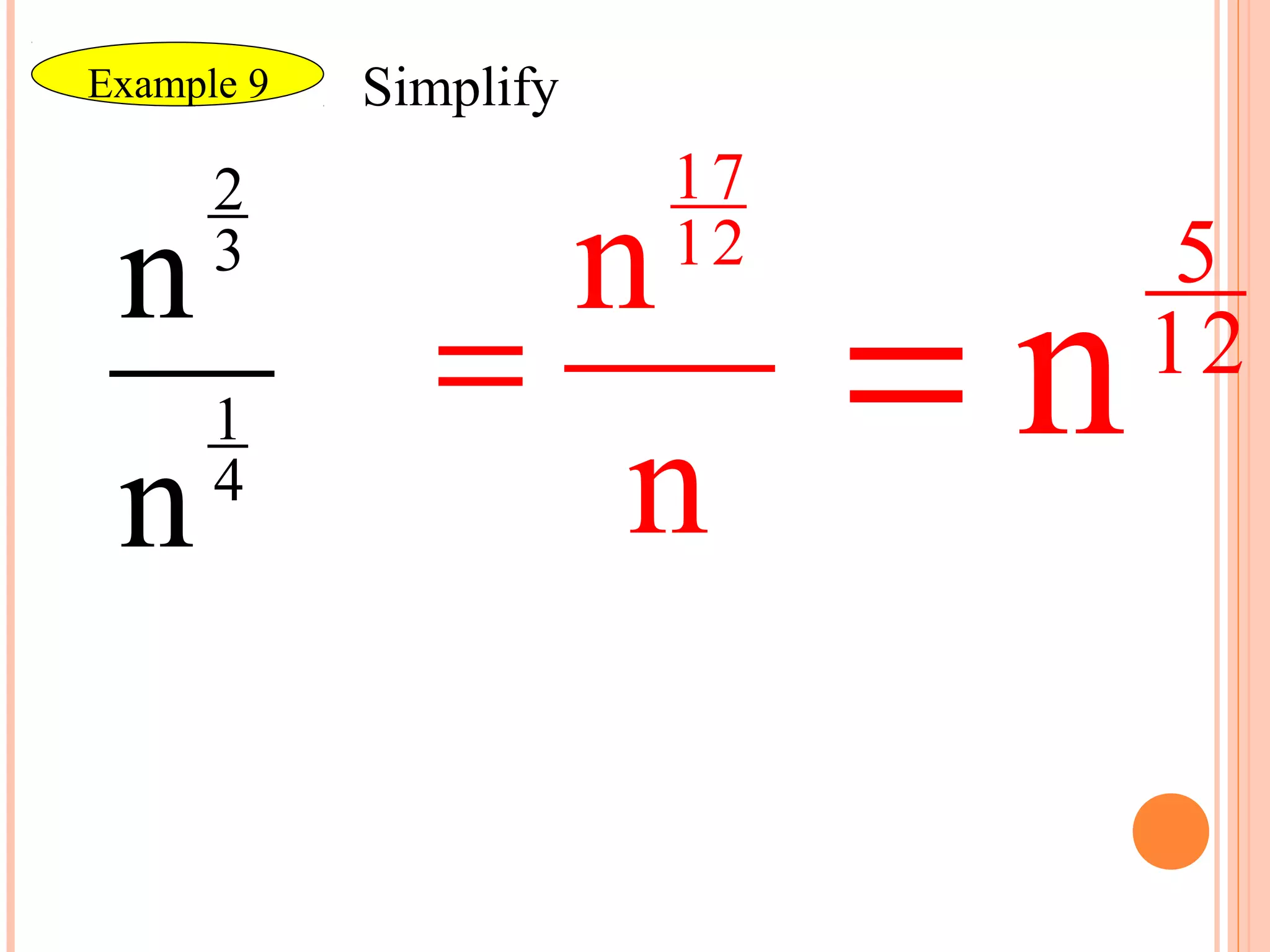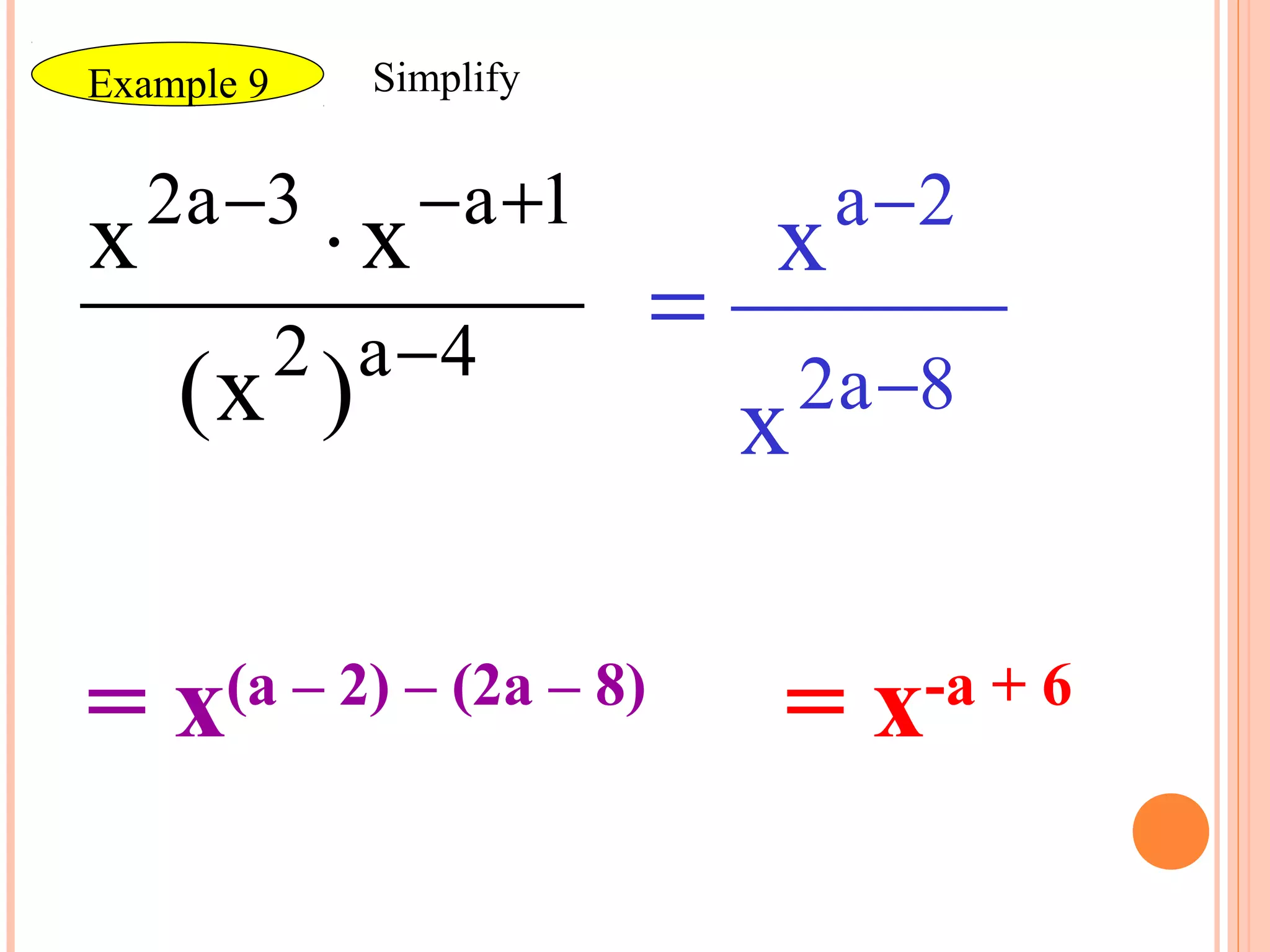Rational exponents allow radicals to be written as fractional exponents. To write a radical with an index of n as a rational exponent, the index becomes the denominator and the exponent of the radicand becomes the numerator. The rules of exponents still apply to rational exponents. Expressions with rational exponents are simplified by having no negative exponents, no fractional exponents in the denominator, not being a complex fraction, and having the least possible index for any remaining radicals. Examples show how to evaluate, simplify, and perform operations on expressions with rational exponents.

2. Review of Exponential Rules

3. Simplifying Expressions with Rational Exponents
Radicals can also be expressed as a rational (or fractional)
power of an expression. It will sometimes be easier to
use this new method of expressing a radical to simplify a
radical expression.
1
b = b
n n
When you see a radical
expression,
you can convert it to a
fractional power.

4. Example 1 Write each expression in Radical Form
1
6
1) x 6
x
2
3 2
2) m 3
m

5. Example 2 Write each radical using Rational Exponents
1
5
1) b b 5
1 5 7
5 7
2) 3
6x y 6 x y
3 3 3

6. Example 3 Evaluate Each Expression
−1 1
1) 49 2
7

7. Rational Exponents
For any nonzero Real number a and
any integers m and n, with n > 1
m
a = ( a) = a
n n m n m

8. Notice: The index of the radical becomes the
denominator of the rational power, and the exponent of the
radicand (expression inside the radical) becomes the
numerator.
Look at these examples:
(1) (2) (3)
power
root
x power
=x ro ot

9. Remember the Rules of Exponents?
They are still valid for rational exponents!!!
Rule Example

10. Example 4 Evaluate
2
(−125) 3
( − 125 )
3 2
25

11. Example 5 Evaluate
−3
 36  2
 
 49 
343
216

12. Simplify
(3a )(− 7a )
Example 6
3 1
2 5
17
− 21a 10

13. Check out how these problems are done
using the rules of exponents:
Evaluate:
Evaluate:

14. Simplify each expression completely
=

15. Expression with Rational Exponents
An expression with Rational Exponents is simplified when:
1. It has no negative exponents
2. It has no Fractional Exponents in the denominator
3. It is not a Complex Fraction
4. The index of any remaining radical is the least
number possible.

16. Simplifying radicals is often Simplify:
easier using rational exponents. 3
Look at this "rational" example,
3
solved two ways. ==>
3
Solved by Rationalizing the Solved by Using
Denominator Rational Exponents

17. Example 7 Simplify
(8x y ) 3
4 2
−1
3
3 1
1
x 4 y 3
1 2 =
2x 4 y 3 2 xy

18. Example 8 Simplify
−7
4
n
3
n 7
n

19. Example 9 Simplify
2 17
n n 12 5
=n
3
1
= 12
n 4
n

20. Example 8 Simplify
Multiply
Change to Same Base Add Exponents
Exponents
Subtract
Exponents
4
2 5
=
4

21. Example 9 Simplify
2 a −3 − a +1 a −2
x ⋅x x
2 a −4
=
(x ) x 2a −8
=x (a – 2) – (2a – 8)
=x -a + 6

22. Example 10 Simplify
1
y +1
2
1
y −1
2
1
y + 2y 2 +1
y −1