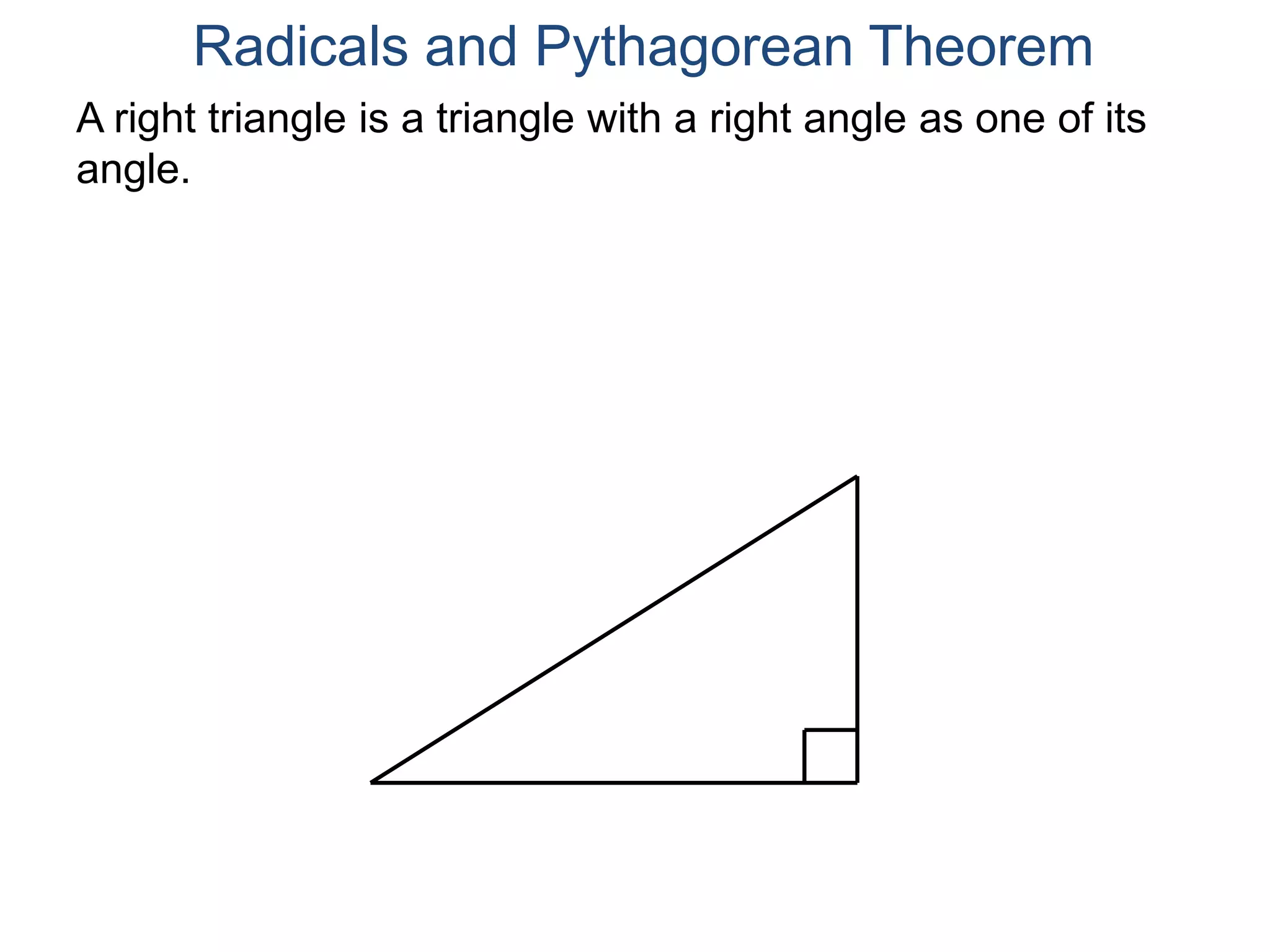
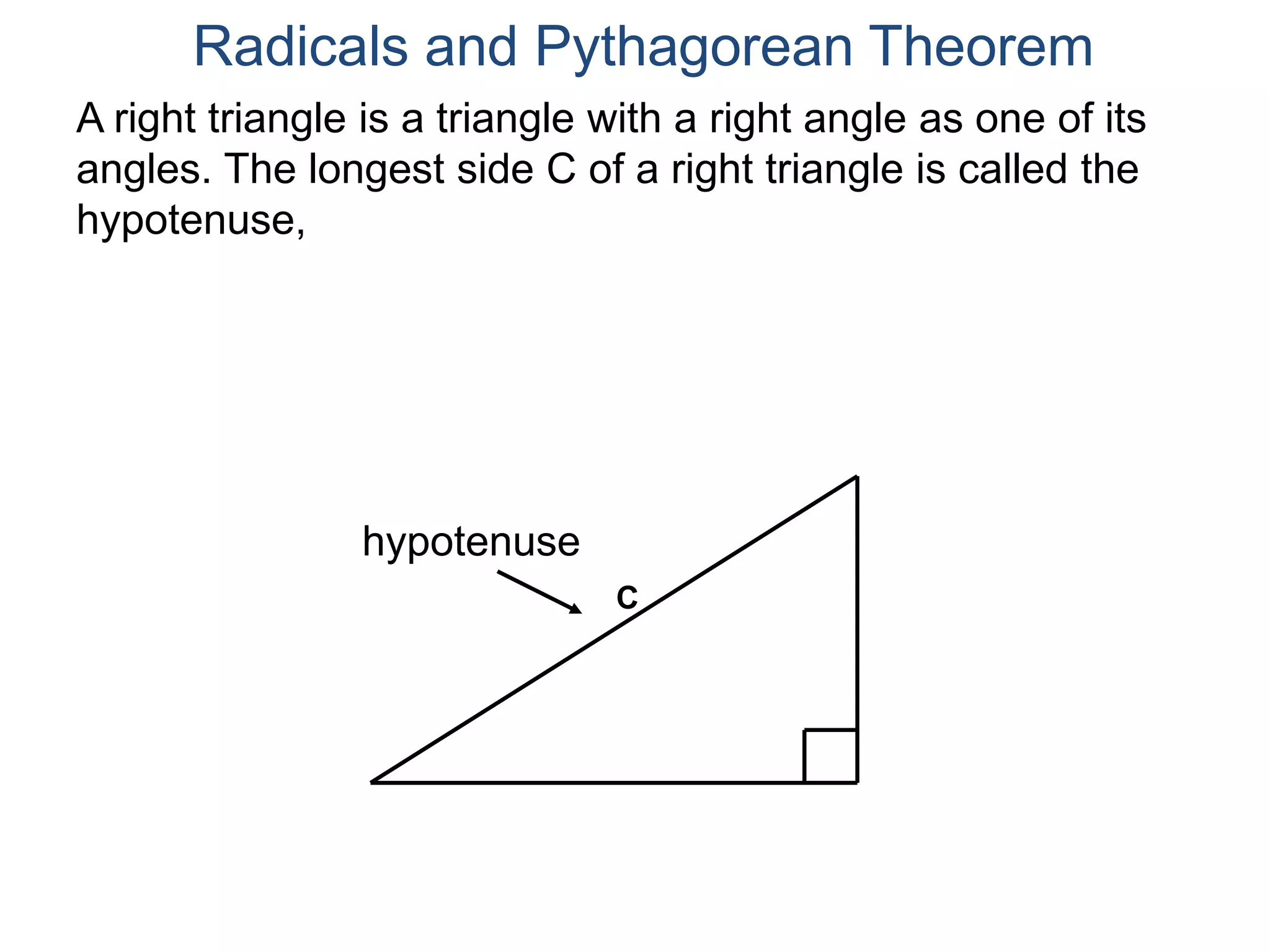
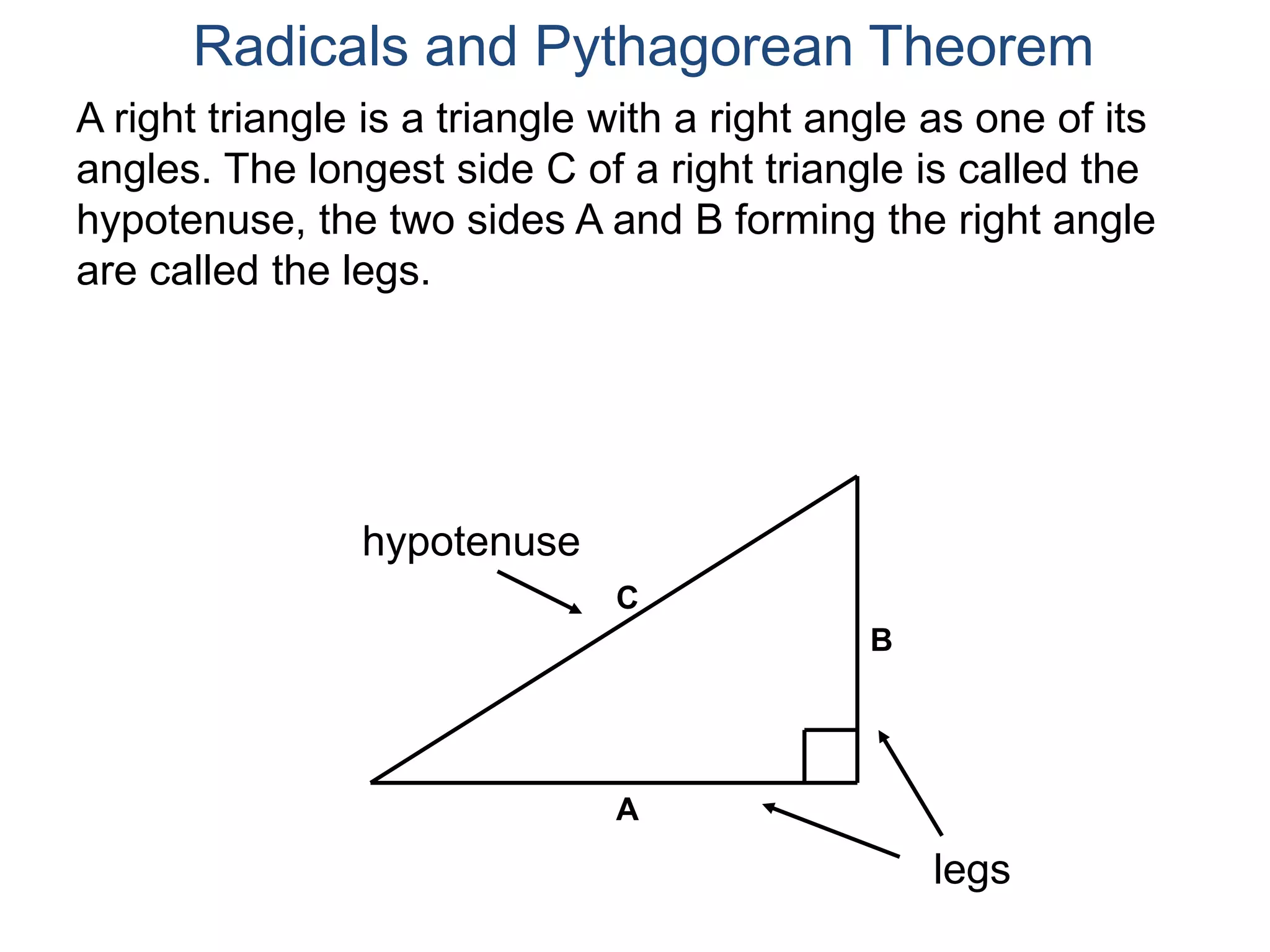
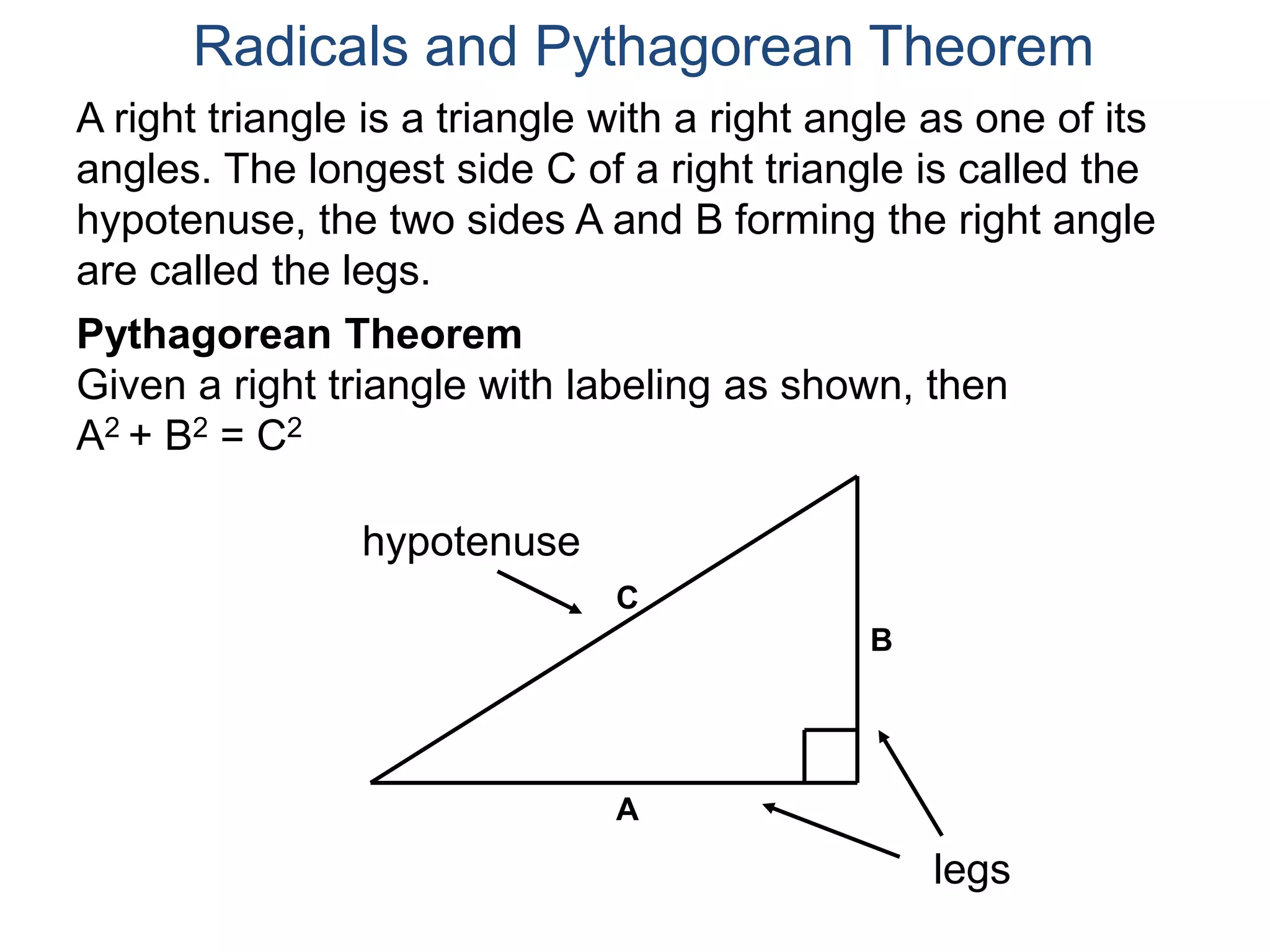
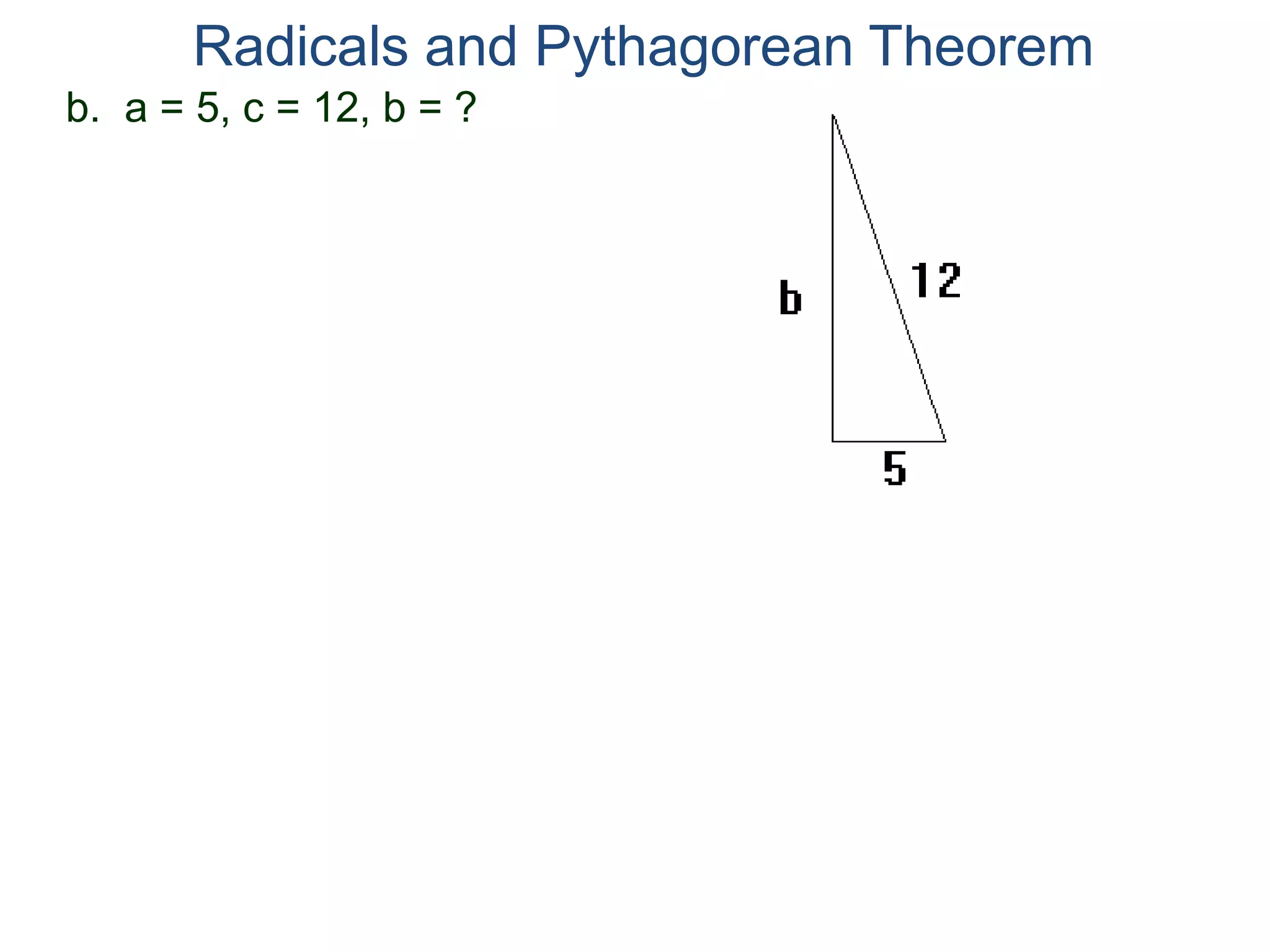
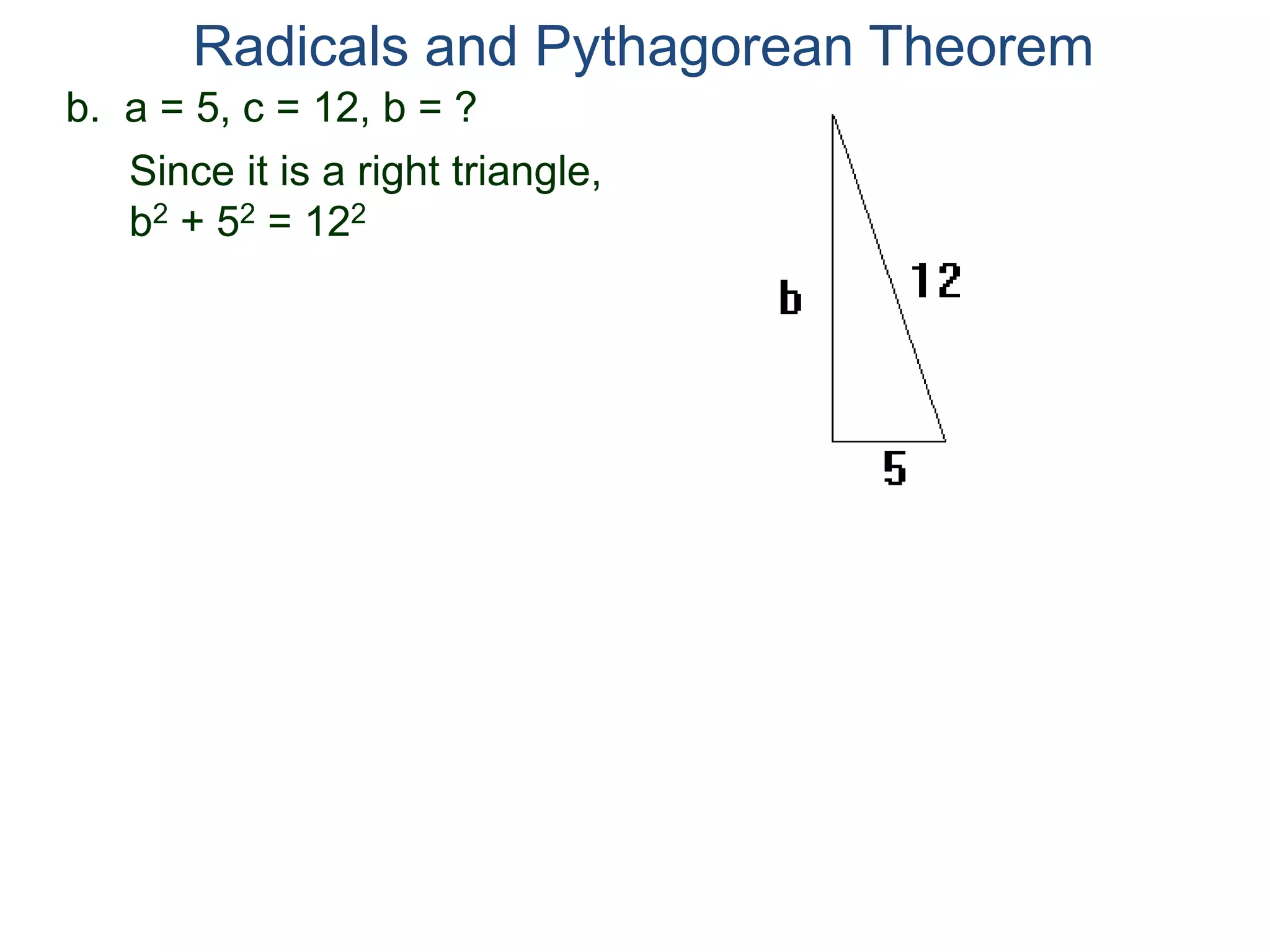
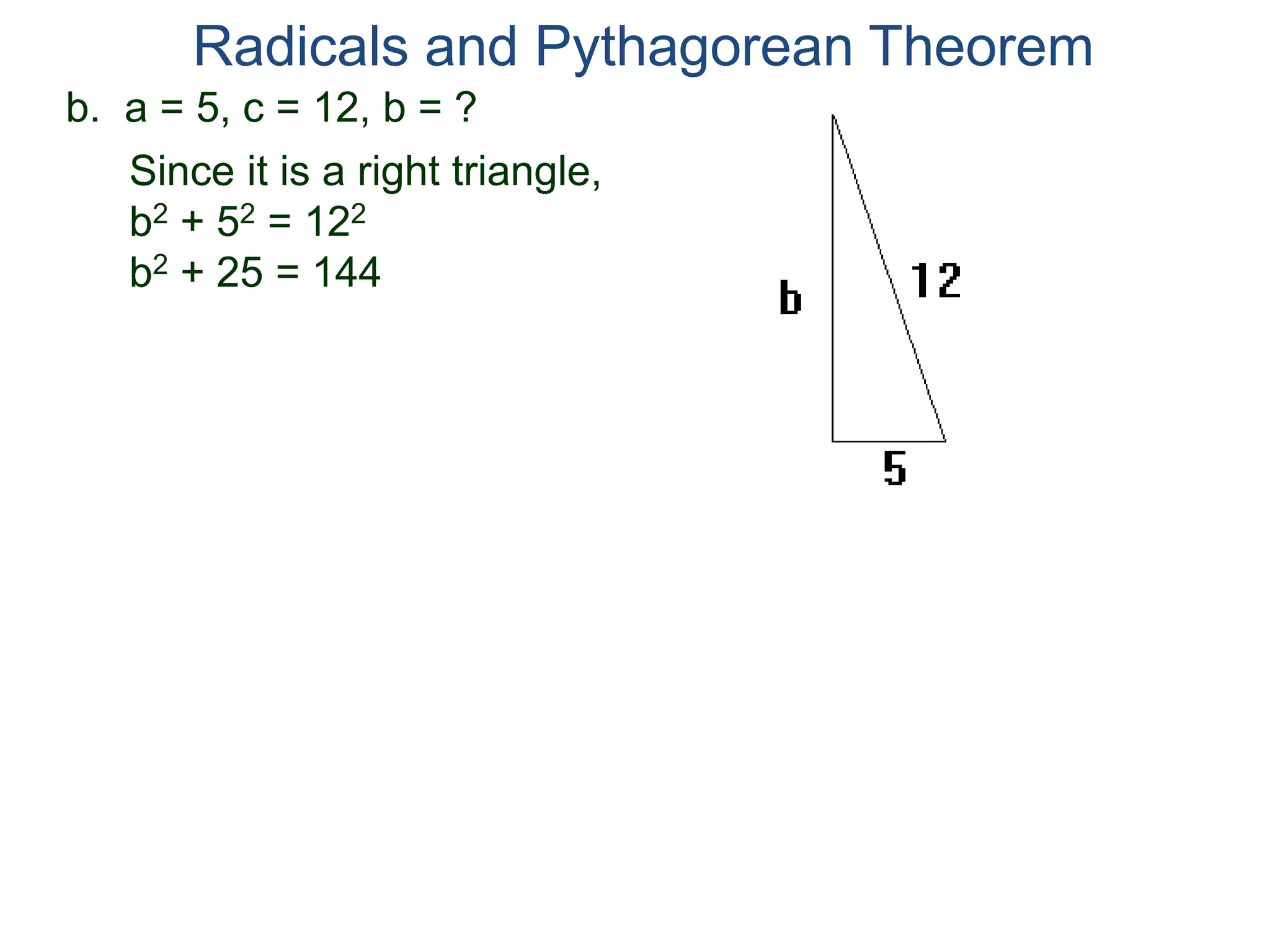
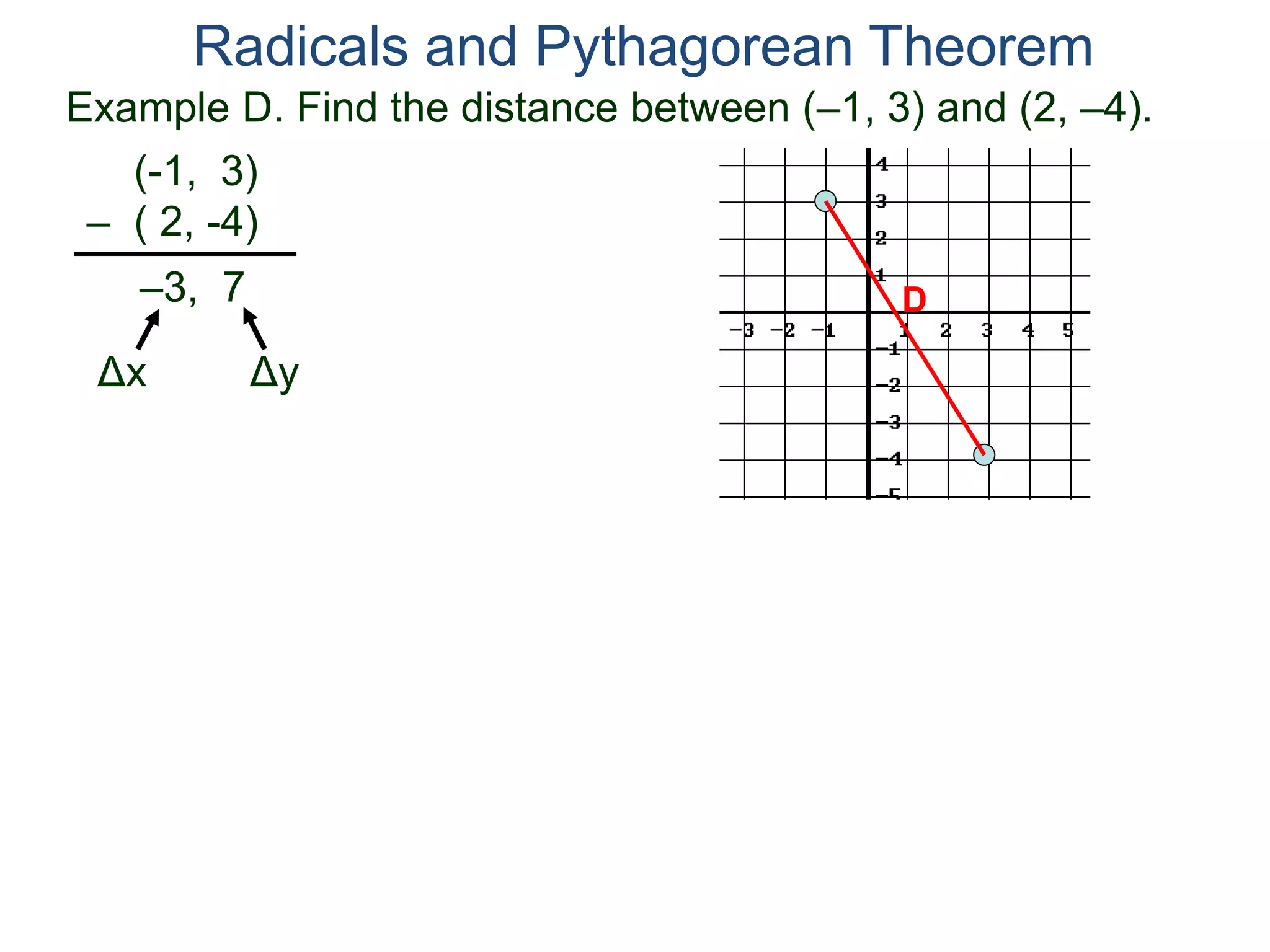
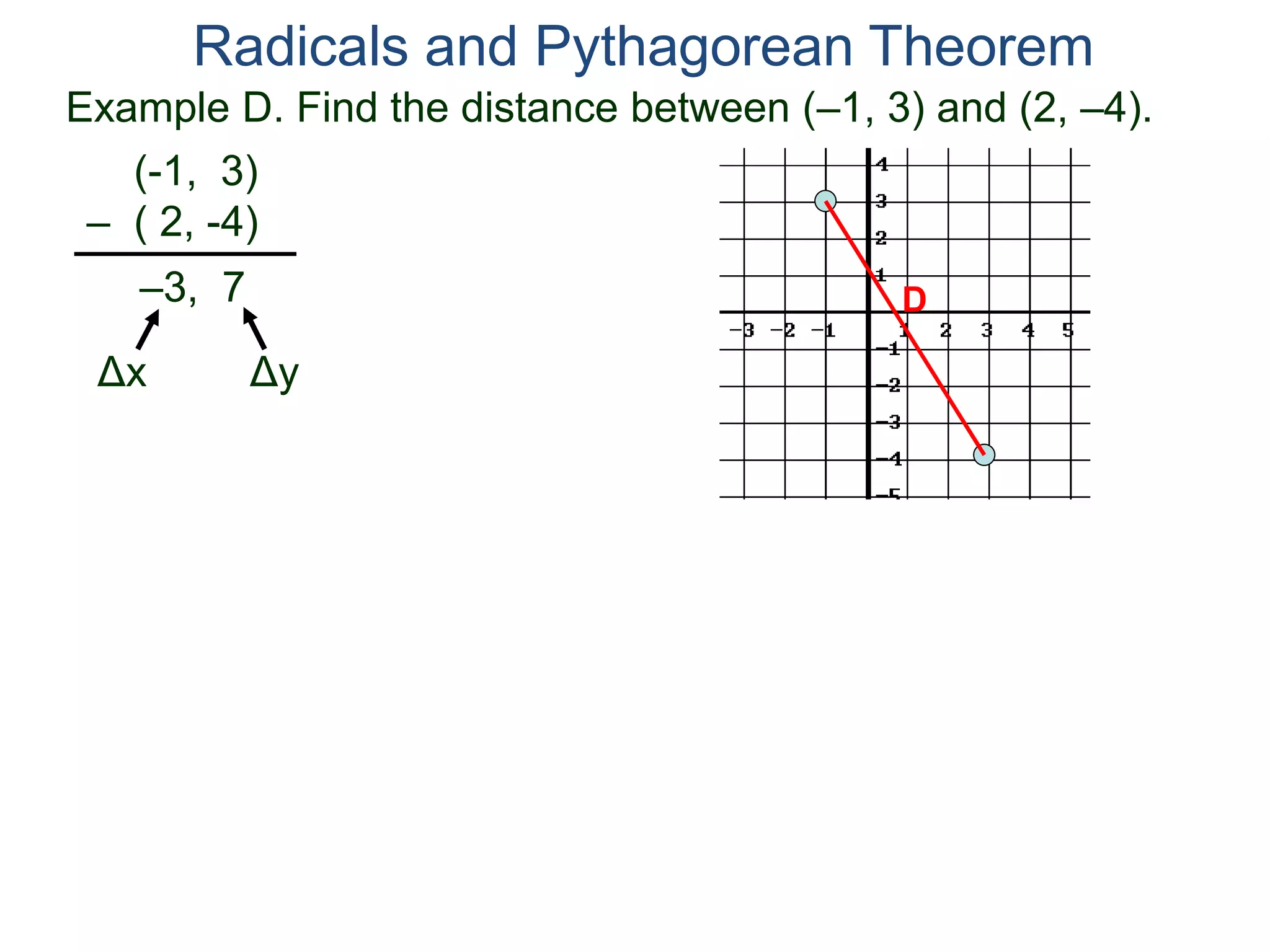
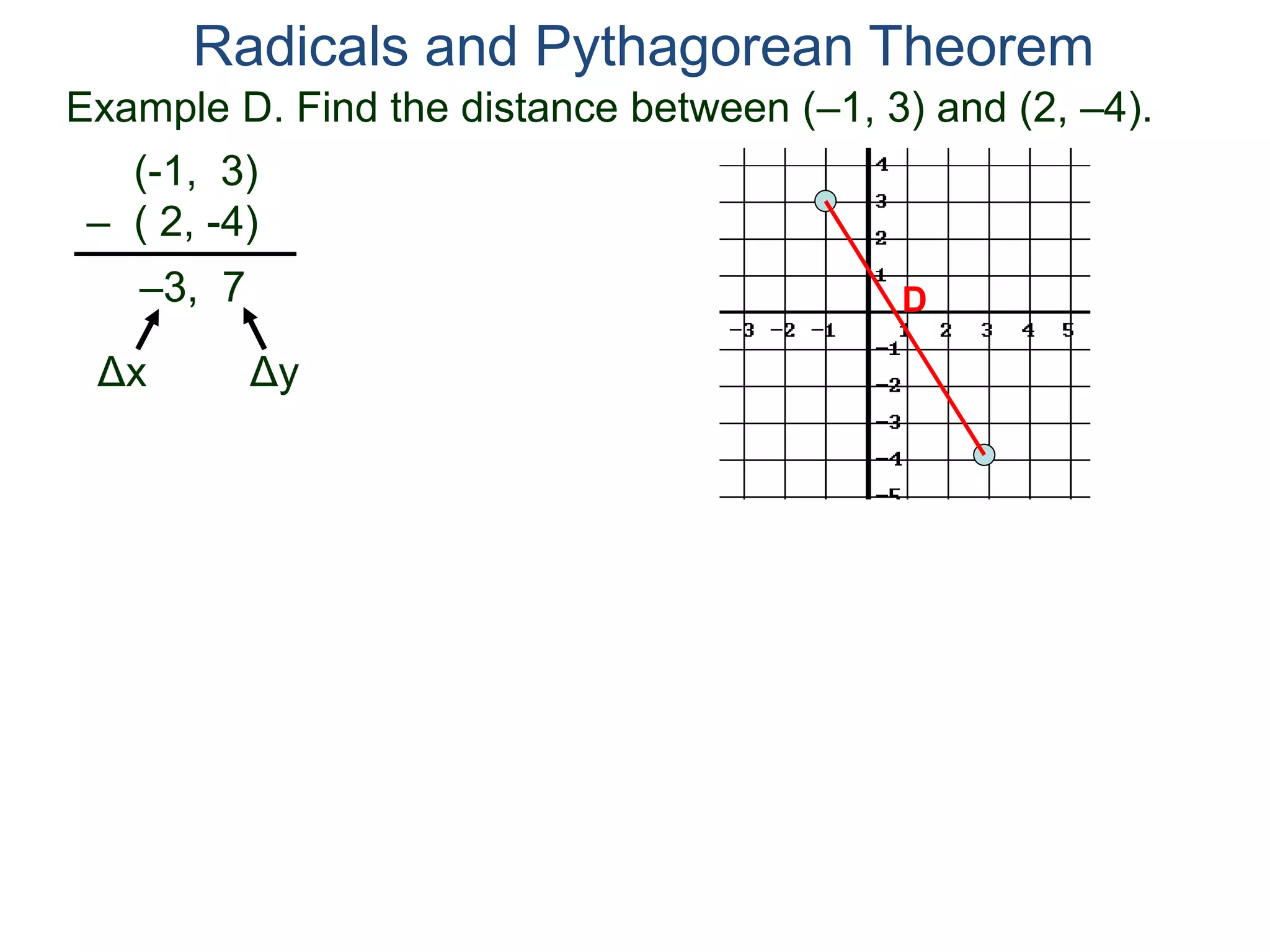
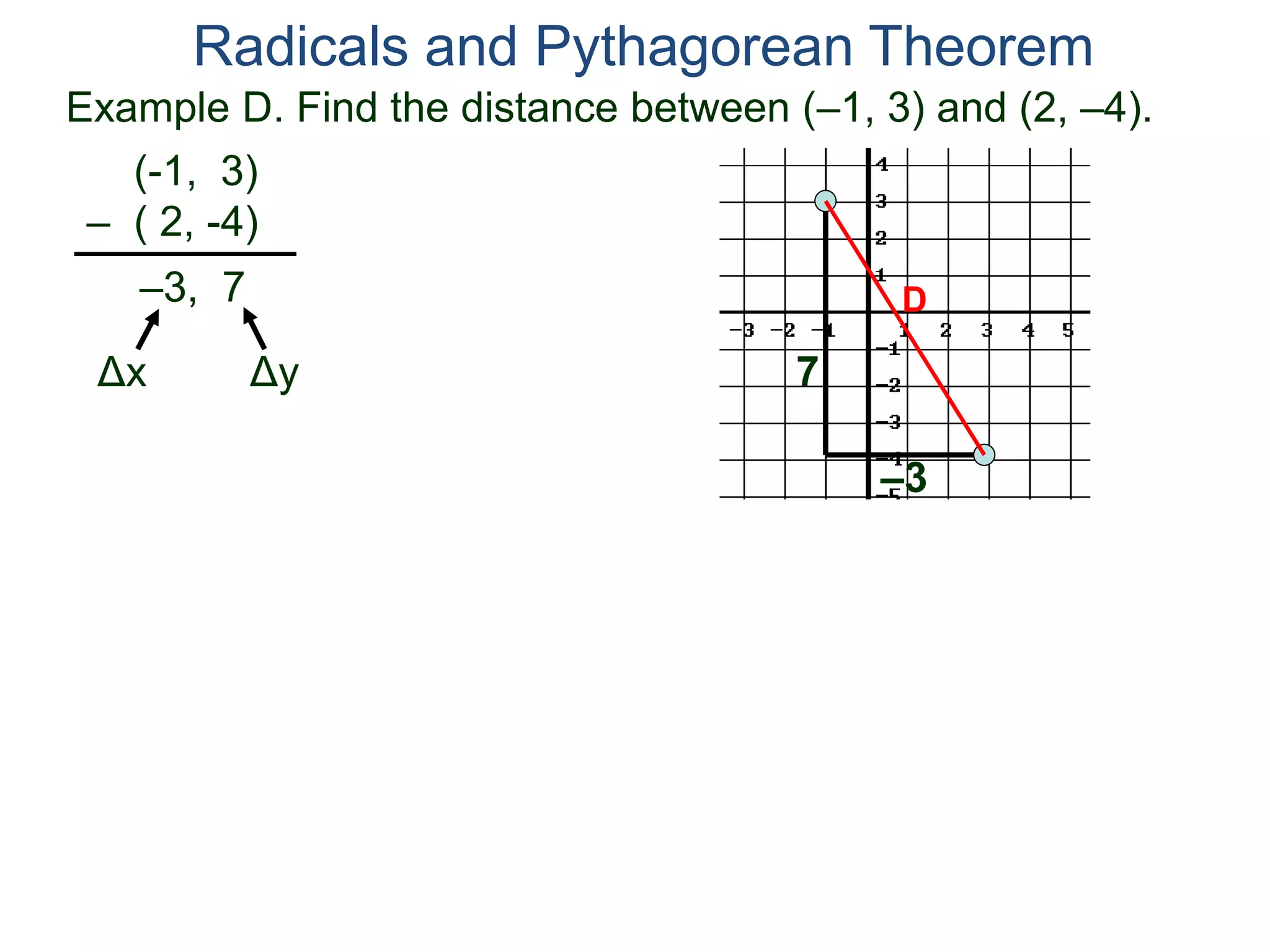
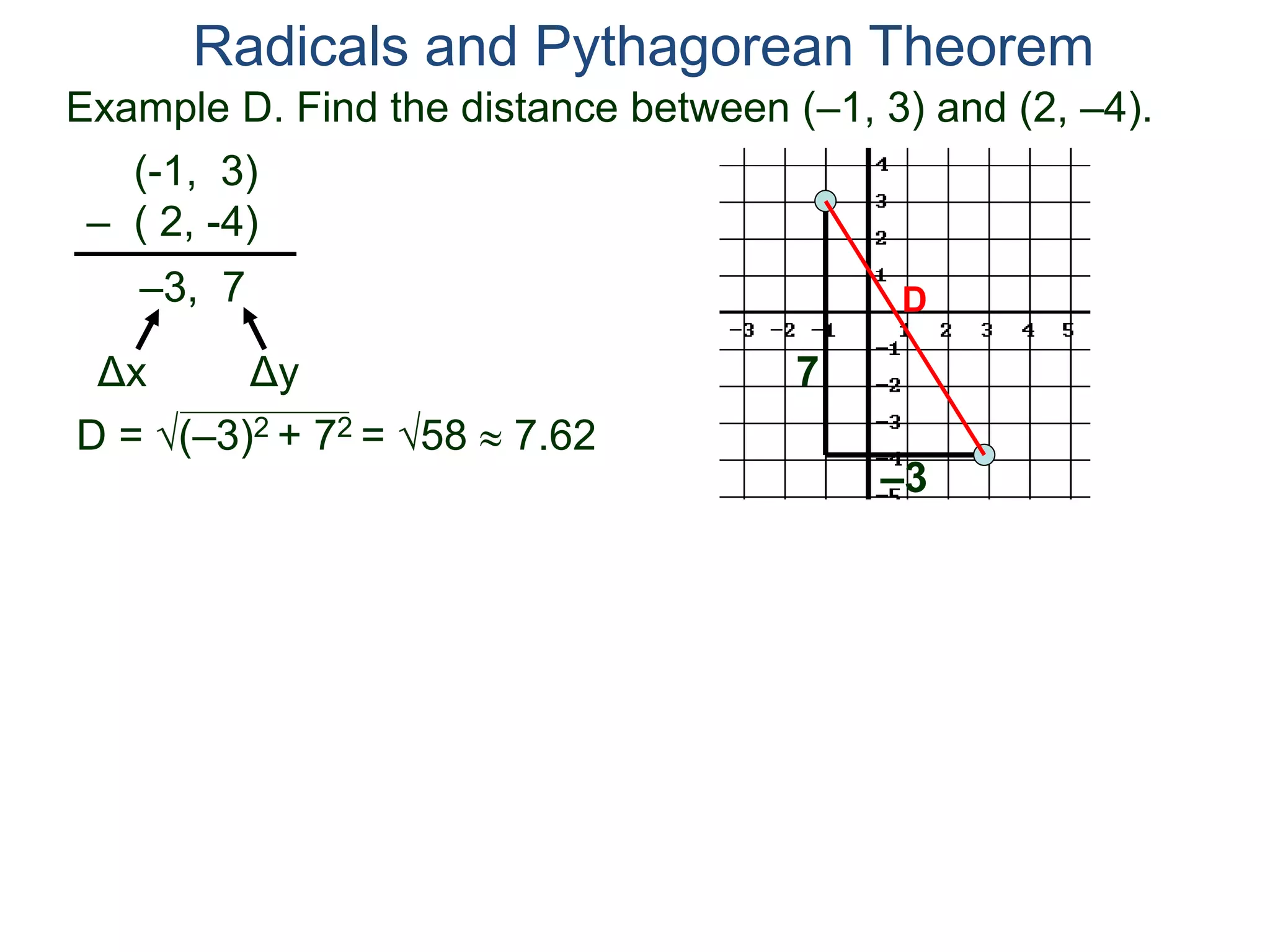
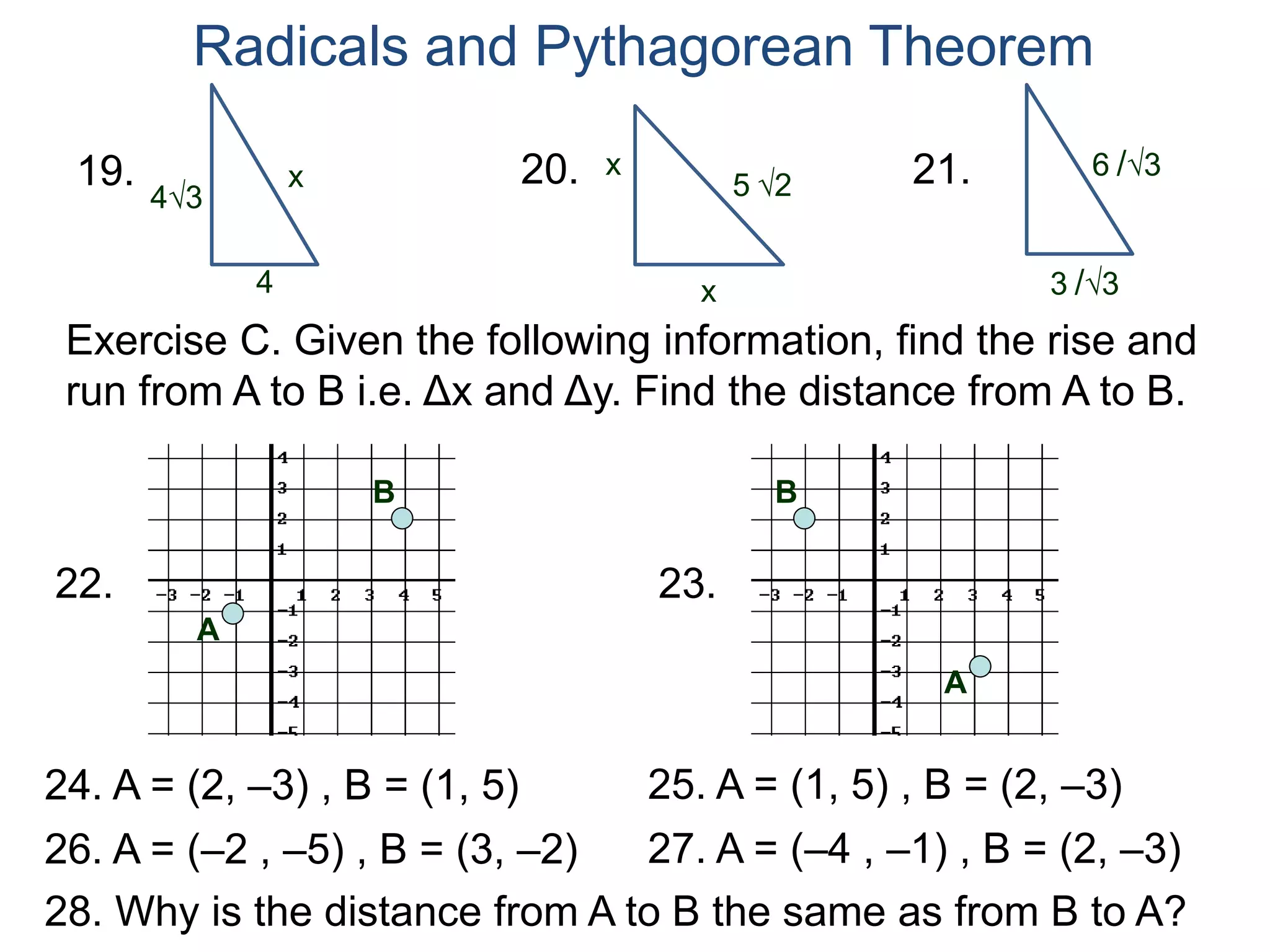
The document discusses square roots and radicals. It defines the square root operation as extracting the number that, when squared, equals the number inside the radical. It provides a table of common square numbers and their square roots that should be memorized. It also describes how to estimate the square root of numbers between known square numbers using the table as a reference.