Embed presentation
Downloaded 22 times










This document provides an overview of linear equations and how to solve them. It defines key characteristics of linear equations, such as variables only having an exponent of 1 and no terms being multiplied together. Various examples of linear and non-linear equations are shown. The document then explains that solving linear equations involves finding the value of the variable that makes both sides equal. It provides step-by-step instructions for solving one-step equations and works through examples of solving multi-step equations. Students are given a checkpoint to practice solving equations on their own before moving to an independent practice section.
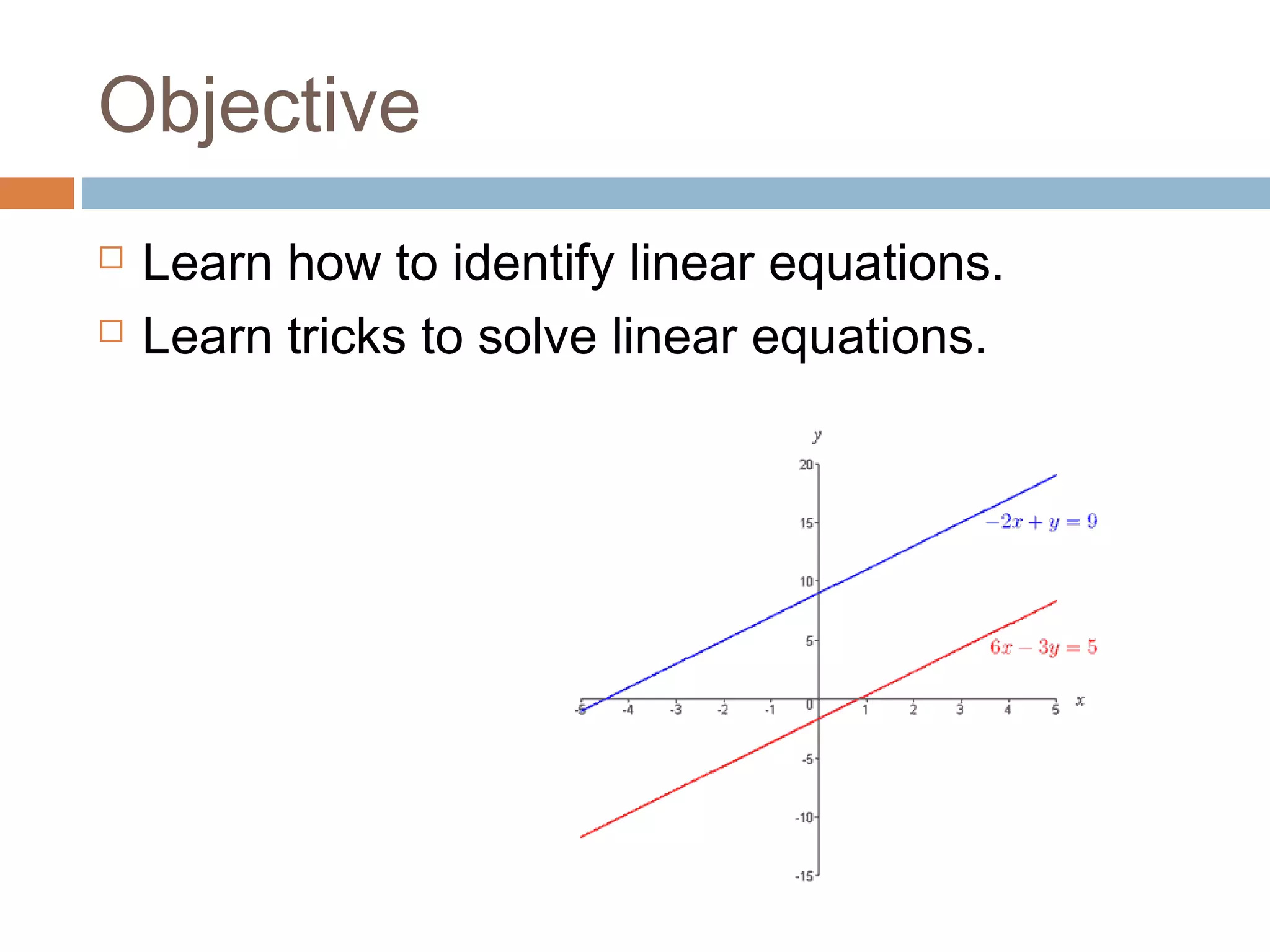
Overview of linear equations and objectives for learning how to identify and solve them.
Key properties of linear equations: always having variables with exponent 1, expressed in Y=mx+b.
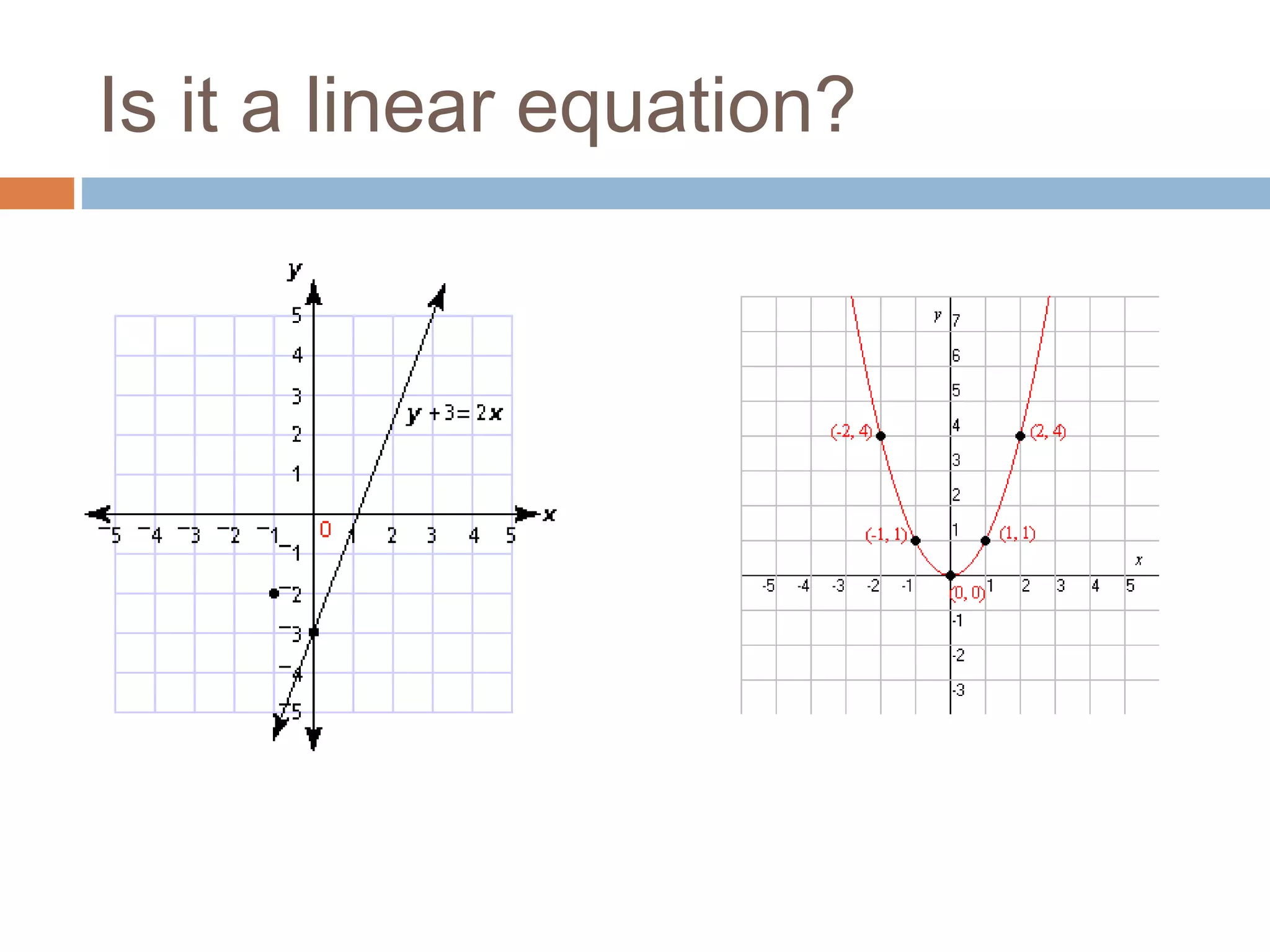
Distinguishing linear functions from non-linear examples, explaining why certain functions are linear.
Defining what it means to solve linear equations, focusing on finding variable values.
Instructions for solving one-step linear equations, including guided practice examples.
Exercises for learners to check their understanding through checkpoint problems.
Series of independent equations for practice, with solutions provided for self-assessment.












