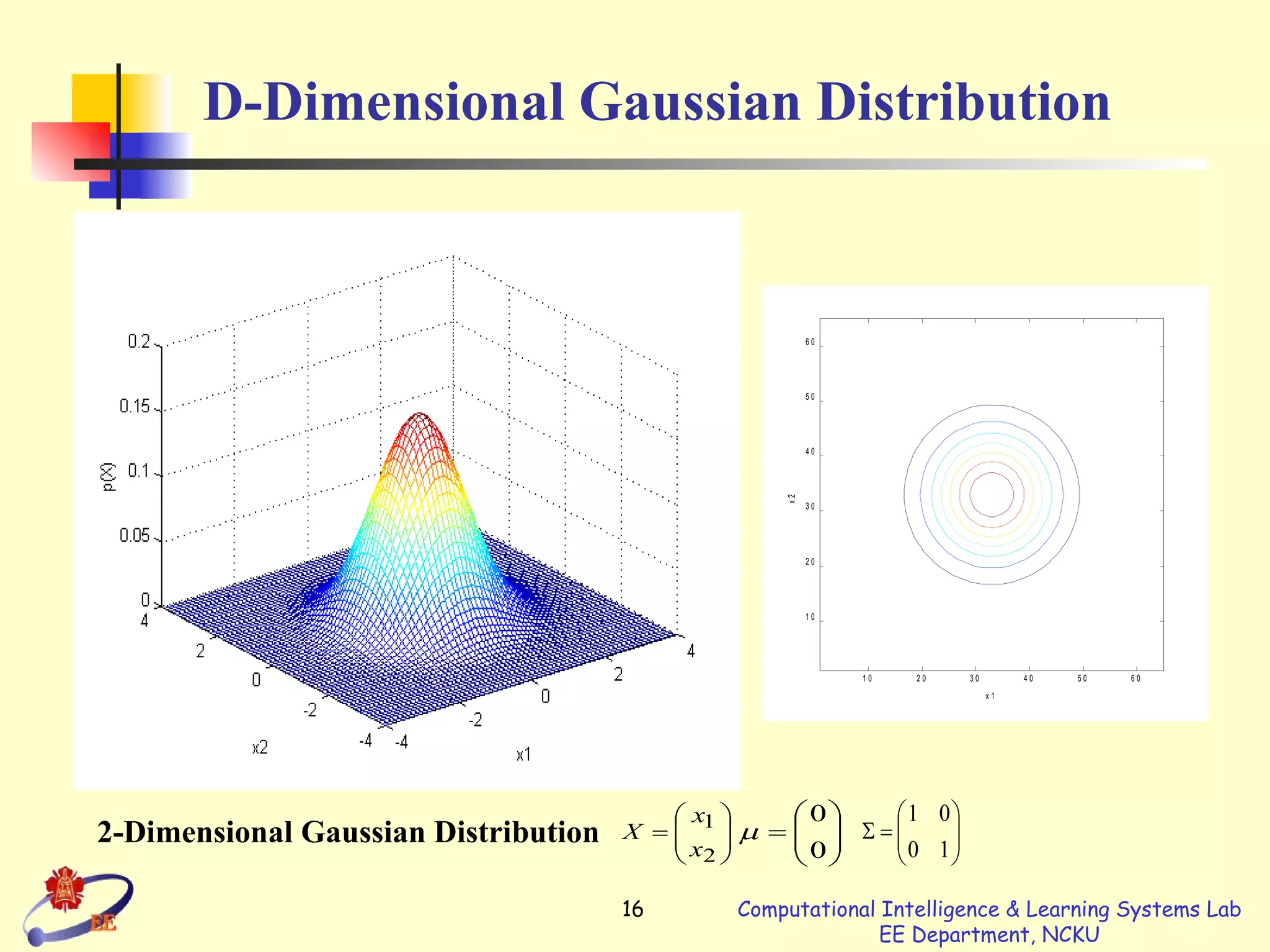
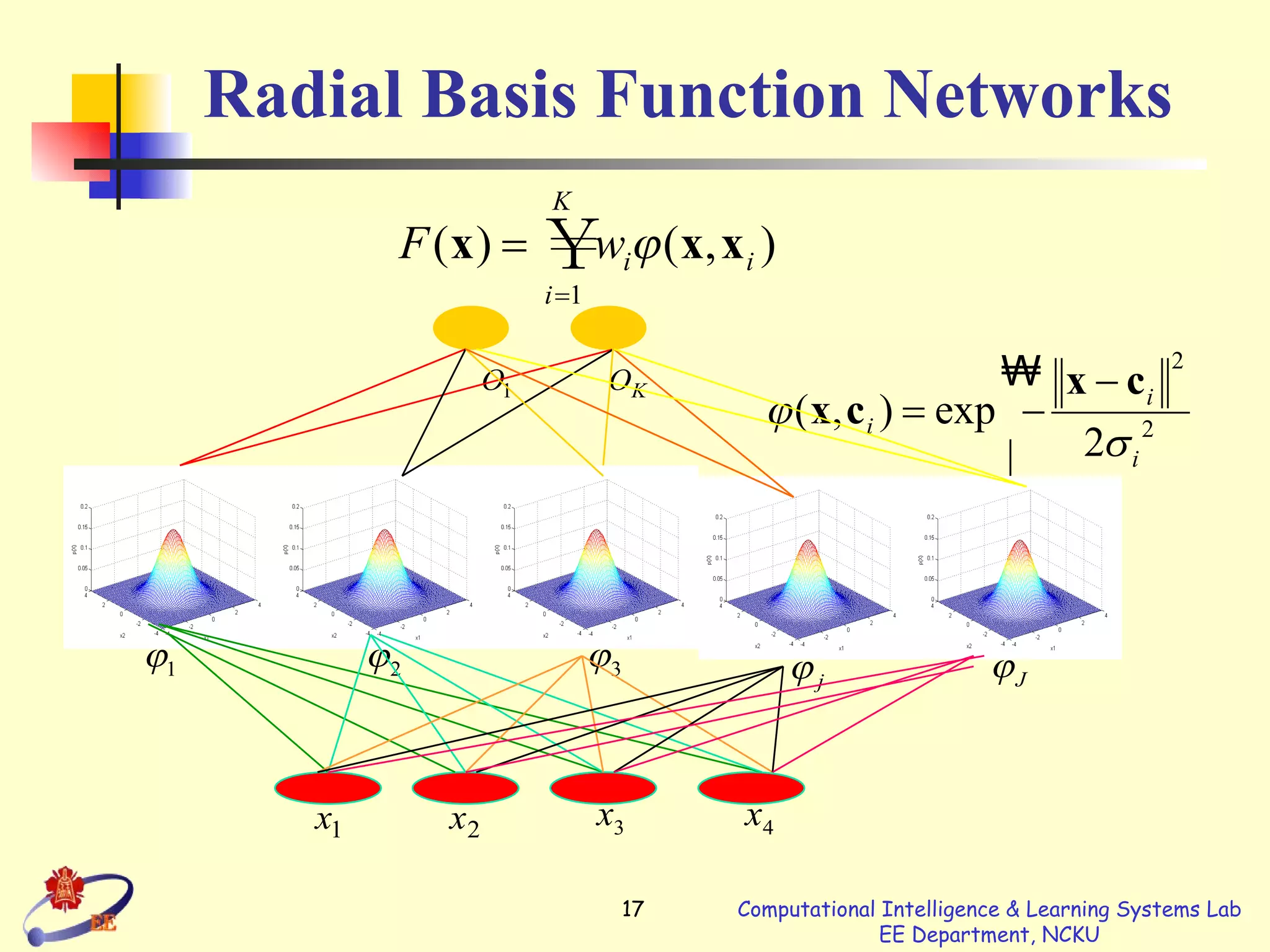
The document summarizes radial basis function (RBF) networks. Key points: - RBF networks use radial basis functions as activation functions and can universally approximate continuous functions. - They are local approximators compared to multilayer perceptrons which are global approximators. - Learning involves determining the centers, widths, and weights. Centers can be randomly selected or via clustering. Widths are usually different for each basis function. Weights are typically learned via least squares or gradient descent methods.

1. Section 5: Radial Basis Function (RBF) Networks Course: Introduction to Neural Networks Instructor: Jeen-Shing Wang Department of Electrical Engineering National Cheng Kung University Fall, 2005

2. Outline Origin: Cover’s theorem Interpolation problem Regularization theory Generalized RBFN Universal approximation Comparison with MLP RBFN = Kernel regression Learning Centers, width, and weights Simulations

3. Origin: Cover’s Theorem A complex pattern-classification problem cast in a high dimensional space nonlinearly is more likely to be linearly separable than in a low dimensional space (Cover, 1965). Cover, T. M., 1965. “Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition.” IEEE transactions on Electronic Computers , EC-14, 326-334

4. Cover’s Theorem Covers’ theorem on separability of patterns (1965) x 1 , x 2 , …, x N , x i   p , are assigned to two classes C 1 and C 2  -separability: where  ( x ) = [  1 ( x ),  2 ( x ), …,  M ( x )] T.

5. Cover’s Theorem (cont’d) Two basic ingredients of Covers’ theorem: Nonlinear functions  ( x ) Dimensions of hidden space ( M ) > Dimensions of input space ( P ) -> probability of separability closer to 1 (a) (b) (c) Linear Separable Spherically Separable Quadrically Separable x x x x x x x x

6. Interpolation Problem Given points ( x i , d i ), x i   p , d i   , 1 ≤ i ≤ N: Find F ( x i ) = d i , 1 ≤ i ≤ N Radial basis function (RBF) technique (Powell, 1988): are arbitrary nonlinear functions Number of functions is the same as number of data points Centers are fixed at known points x i .

7. Interpolation Problem (cont’d) Matrix form: Vital question: Is  non-singular? where

8. Michelli’s Theorem If points x i are distinct,  is non-singular (regardless of the dimension of the input space) Valid for a large class of RBF functions:

9. Learning: Ill and Well Posed Problems Given a set of data points, learning is viewed as a hypersurface reconstruction or approximation problem---inverse problem Well posed problem A mapping from input to output exists for all input values The mapping is unique The mapping function is continuous Ill posed problem Noise or imprecision data adds uncertainty to reconstruct the mapping uniquely Not enough training data to reconstruct the mapping uniquely. Degraded generalization performance Regularization is needed

10. Regularization Theory The basic idea of regularization is to stabilize the solution by means of some auxiliary functions that embeds prior information, e.g., smoothness constraints on the input-output mapping (i.e., solution to the approximation problem), And thereby make an ill-posed problem into a well-posed one. (Poggio and Girosi, 1990).

11. Solution to the Regularization Problem Minimize the cost function E ( F ) w.r.t F Standard error term Regularizing term where  is the regularization parameter

12. Solution to the Regularization Problem Poggio & Griosi (1990): If C ( F ) is a (problem-dependent) linear differential operator, the solution to

13. Interpolation vs Regularization Interpolation Exact interpolator Possible RBF Regularization Exact interpolator Equal to the “interpolation” solution if  = 0 Example of Green’s function

14. Generalized RBF Network (GRBFN) As many radial basis functions as training patterns Computationally intensive Ill-conditioned matrix Regularization is not easy ( C ( F ) is problem-dependent) Possible solution -> Generalized RBFN approach Adjustable parameters

15. D-Dimensional Gaussian Distribution d -Dimensional Gaussian Distribution ( ind. each other) (General form)

16. D-Dimensional Gaussian Distribution 2-Dimensional Gaussian Distribution

17. Radial Basis Function Networks

18. RBFN: Universal Approximation Park & Sandberg (1991): For any continuous input-output mapping function f ( x ) The theorem is stronger (radial symmetry is not needed) K is not specified Provides a theoretical basis for practical RBFN!

19. Kernel Regression Consider the nonlinear regression model : Recall: From probability theory, By using (2) in (1),

20. Kernel Regression We do not know the , which can be estimated by Parzen-Rosenblatt density estimator :

21. Kernel Regression Integration and by using , and using the symmetric property of K , we get :

22. Kernel Regression By using (4) and (5) as estimates of part of (3) :

23. Nadaraya-Watson Regression Estimator By define the normalized weighting function : We can rewrite (6) as : F ( x ) : a weighted average of the y -observables

24. Normalized RBF Network Assume the spherical symmetry of K (x), then : Normalized radial basis function is defined:

25. Normalized RBF Network let for all i , we may rewrite (6) as : may be interpreted as the probability of an event x conditional on x i

26. Multivariate Gaussian Distribution If we take the kernel function as the multivariate Gaussian Distribution : Then we can write :

27. Multivariate Gaussian Distribution And the NRBF is: The centers of the RBF coincide with the data points

28. RBFN vs MLP RBFN Single hidden layer Nonlinear hidden layer and linear output layer Argument of hidden units: Euclidean norm Universal approximation property Local approximators MPL Single or multiple hidden layers Nonlinear hidden layer and linear or nonlinear output layer Argument of hidden units: scalar product Universal approximation property Global approximators

29. Learning Strategies Parameters to be determined: w i , c i , and  i Traditional learning strategy: splitted computation Centers, c i Widths,  i Weights, w i

30. Computation of Centers Vector quantization: Centers c i must have the density properties of training patterns x i Random selection from the training set Competitive learning Frequency-sensitive learning Kohonen learning This phase only uses the input ( x i ) information, not the output ( d i )

31. K -Means Clustering k ( x ) = index of best-matching (winning) neuron: M = number of clusters where t k ( n ) = location of the k th center.

32. Computation of Widths Universal approximation property: valid with identical widths In practice (limited training patterns), variables widths  i One approach: Use local clusters Select  i according to the standard deviation of clusters

33. Computation of Widths (cont’d.) Red-dotted line: Estimated distribution Blue-solid line: Actual distribution

34. Computation of Weights (SVD) Problem becomes linear! Solution of least square criterion In practice, use SVD Keep Constant

35. Computation of Weights (Gradient Descent) Linear weights (output layer) Positions of centers (hidden layer) Widths of centers (hidden layer)

36. Summary Learning is finding surface in multidimensional space best fit to training data Approximate function with linear combination of Radial basis functions F ( x ) =  w i G (|| x - x i ||) i = 1, 2, … , N G (|| x - x i ||) is called a Green function It can be a uniform or Gaussian function . When N = number of sample, we call it regularization network When N < number of sample, it is a radial basis function network