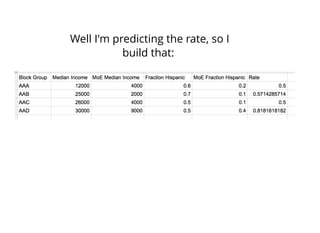
1. The document discusses four case studies of mistakes the author made in data science projects. The first case involved incorrectly predicting mail return rates without considering sample sizes. The second was backtesting a trading strategy without accounting for data leakage. The third was developing statistical software without proper testing. The fourth was incorrectly calculating an A/B test statistic without considering sample size. 2. In each case, the author explains what went wrong and the lessons learned, such as considering sample sizes, understanding where data comes from, testing software appropriately, and not compounding uncertainties when calculating statistics. The author also discusses potential pitfalls in machine learning, like incorrectly sparsifying models or using PCA before regression.

1. Mistakes I've MadeMistakes I've Made
PyData Seattle 2015
Cam Davidson-Pilon

3. Who am I?Who am I?
Cam Davidson-Pilon
- Lead on the Data Team at Shopify
- Open source contributer
- Author of Bayesian Methods for Hackers
(in print soon!)

5. Ottawa

6. Ottawa

7. Ottawa?

8. Case Study 1Case Study 1

9. We needed to predict mail return
rates based on census data.
Sample Data (simplified):

10. Well I'm predicting the rate, so I
build that:

11. Don't need margin of errors...

12. ...then do "data science"

13. Outcome: failure
What went wrong? At the time, ¯_(ツ)_/¯

14. (highly, highly recommended!)

15. σ =X¯
√n
σ

16. σ =X¯
√n
σ
"The std. deviation of the sample mean is
equal to the std. deviation of the
population over square-root n"

20. What I learned
1. Sample sizes are so important when dealing with
aggregate level data.
2. It was only an issue because the sample sizes were
different, too.
3. Use the Margin of Error, don't ignore it - it's there for a
reason.
4. I got burned so bad here, I became a Bayesian soon after.

21. Case Study 2Case Study 2
A intra-day time series of S&P, Dow,
Nasdaq and FTSE (UK index)

22. Suppose you are
interested in doing some
day trading. Your target:
UK stocks.
Futures on the FTSE in
particular.

24. Post Backtesting Results

25. Push to Production -
investing really money

26. What happened?
Data Leakage happened

28. What I learned
1. Your backtesting / cross validation will always be equal or
overly optimistic - plan for that.
2. Understand where your data comes from, from start to
finish.

29. Case Study 3Case Study 3

30. What I learned
1. When developing statistical software that already exists in
the wild, write tests against the output of that software.
2. Be responsible for your software:

31. Case Study 4Case Study 4

32. It was my first A/B test at
Shopify...
Control group: 4%
Experiment group: 5%
Bayesian A/B testing told me there was a
significant statistical difference between
the groups...

33. Upper management wanted
to know the relative increase...
(5% - 4%) / 4% = 25%

34. No.
We forgot sample size
again.

39. What I learned
1. Don't naively compute stats on top of stats - this only
compounds the uncertainty.
2. Better to underestimate than overestimate
3. Visualizing uncertainty is a the role of a statistician.

40. Machine LearningMachine Learning
counter examplescounter examples

41. Sparse-ing the
solution naively

42. Coefficients after linear regression*:
*Assume data has been normalized too,
i.e. mean 0 and standard deviation 1

43. Decide to drop a variable:

45. Suppose this is the true model...
Okay, out regression got the coefficients
right, but...

46. So actually, together, these variables have
very little contribution to Y!

47. Solution:
Any form of regularization will solve this.
For example, using ridge regression with
with even the slightest penalizer gives:

49. PCA before
Regression

50. PCA is great at many things, but it can
actually significantly hurt regression if
used as a preprocessing step. How?

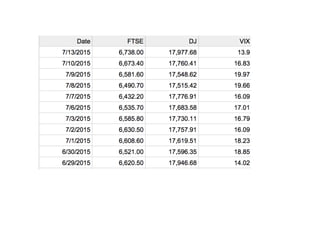
51. Suppose we wish to regress Y onto X and W.
The true model of Y is Y = X - W. We don't know this
yet.
Suppose further there is a positive
correlation between X and W, say 0.5.
Apply PCA to [X W], we get a new matrix:
[ X + W, X − W]√2
1
√2
1
√2
1
√2
1

52. [ X + W, X − W]√2
1
√2
1
√2
1
√2
1
Textbook analysis tells you to drop the
second dimension from this new PCA.

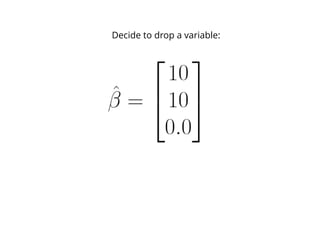
53. [ X + W]√2
1
√2
1
So now we are regressing Y onto:
i.e., find values to fit the model:
Y = α + β(X + W)
But there are no good values for these
unknowns!

54. Quick
IPython
Demo

55. Solution:
Don't use naive PCA before regression, you
are losing information - try something like
supervised PCA, or just don't do it.

56. Thanks for listening :)
@cmrn_dp