A binary tree is composed of nodes where each node contains a value and pointers to its left and right children. A binary tree traversal involves systematically visiting each node by traversing either breadth-first or depth-first. Breadth-first traversal visits nodes by level while depth-first traversal can be pre-order, in-order, or post-order depending on when the node is visited. Threaded binary trees reduce the number of null pointers by using them to point to other nodes for more efficient traversals.

1. DATA AND FILE STRUCTURES
LECTURE 4

2. Binary tree
• A binary tree is composed of zero or more nodes
• Each node contains:
– A value (some sort of data item)
– A reference or pointer to a left child (may be null), and
– A reference or pointer to a right child (may be null)
• A binary tree may be empty (contain no nodes)
• If not empty, a binary tree has a root node
– Every node in the binary tree is reachable from the root node
by a unique path
• A node with neither a left child nor a right child is
called a leaf
– In some binary trees, only the leaves contain a value

3. Picture of a binary tree
a
b c
d e
g h i
l
f
j k

4. Size and depth
• The size of a binary tree
is the number of nodes in
it
– This tree has size 12
• The depth of a node is its
distance from the root
– a is at depth zero
– e is at depth 2
• The depth of a binary tree
is the depth of its deepest
node
– This tree has depth 4
a
b c
d e f
g h i j k
l

5. Tree Example: UNIX Directory

6. Binary Tree Example: Expression
Trees
• Leaves are operands (constants or variables)
• The internal nodes contain operators
• Will not be a binary tree if some operators are not
binary

7. Tree Traversal (Definition)
• The process of systematically visiting all the
nodes in a tree and performing some
computation at each node in the tree is called a
tree traversal.
• There are two methods in which to traverse a
tree:
1. Breadth-First Traversal.
2. Depth-First Traversal:
• Preorder traversal
• Inorder traversal (for binary trees only)
• Postorder traversal

8. Tree Traversal Methods
• Pre-order
1. Visit node // first
2. Recursively visit left subtree
3. Recursively visit right subtree
• In-order
1. Recursively visit left subtree
2. Visit node // second
3. Recursively right subtree
• Post-order
1. Recursively visit left subtree
2. Recursively visit right subtree
3. Visit node // last

9. Preorder, Postorder and Inorder
Pseudo Code

10. Depth-first Preorder Traversal
H
D
B
A C E G I K M O
N
L
JF
H D B A C F E G L J I K N M O
N-L-R

11. Depth-first Inorder Traversal
H
D
B
A C E G I K M O
N
L
JF
L-N-R
A B C D E F G H I J K L M N O
Note: An inorder traversal of a BST visits the keys sorted in increasing order.

12. Depth-first Postorder Traversal
H
D
B
A C E G I K M O
N
L
JF
L-R-N
A C B E G F D I K J M O N L H

13. Tree Traversal Methods
• Breadth-first
BFS(Node n) {
Queue Q = new Queue();
Q.enqueue(n); // insert node into Q
while ( !Q.empty()) {
n = Q.dequeue(); // remove next node
if ( !n.isEmpty()) {
visit(n); // visit node
Q.enqueue(n.Left()); // insert left subtree in Q
Q.enqueue(n.Right()); // insert right subtree in Q
} }

14. Breadth-First Traversal
H
D
B
A C E G I K M O
N
L
JF
H D L B F J N A C E G I K M O

15. Tree Traversal Examples
• Pre-order (prefix)
– + × 2 3 / 8 4
• In-order (infix)
– 2 × 3 + 8 / 4
• Post-order (postfix)
– 2 3 × 8 4 / +
• Breadth-first
– + × / 2 3 8 4
+
× /
2 3 8 4
Expression tree

16. Tree Traversal Examples
• Pre-order
– 44, 17, 32, 78,
50, 48, 62, 88
• In-order
– 17, 32, 44, 48,
50, 62, 78, 88
• Post-order
– 32, 17, 48, 62,
50, 88, 78, 44
• Breadth-first
– 44, 17, 78, 32,
50, 88, 48, 62
88
44
17 78
32 50
48 62
Binary search tree
Sorted
order!

17. Binary Tree Sort
• The Binary Tree Sort works on a simple
concept: The value at the root of a tree is
always greater than all the values in its left
subtree and less than or equal to all the
values in its right subtree.
• We can search for a value by comparing
that value to the root, and if the value is
smaller, examine the left subtree, and if the
value is larger examine the right subtree.

18. Binary Tree Sort
• Of course, if the values are equal, you've
found it!
•The maximum number of comparisons is
directly related to the height of the tree.
• But in a tree of height 20 (at most 20
comparisons) we might have 220
or about a
million items!

19. Binary Tree Sort
• The first step, then, is to take all the values
and build a binary search tree.
• The basis of this process is a function to
insert a new value into an existing binary
search tree.

20. left subtree exists?
YES
NO
attach value
as a left
subtree
try the left
subtree
Binary Tree Sort
value < value at root?
NO
YES
right subtree exists?
YES NO
attach value
as a right
subtree
try the right
subtree
Value must be in
the left subtree
Value must be in
the right subtree

21. Binary Search Trees (BST)
• A data structure for efficient searching,
inser-tion and deletion
• Binary search tree property
– For every node X
– All the keys in its left
subtree are smaller than
the key value in X
– All the keys in its right
subtree are larger than the
key value in X

22. Binary Search Trees
A binary search tree Not a binary search tree

23. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.

24. INORDER-TREE-WALK(x)
if x != NIL
INORDER-TREE-WALK(left[x])
print key[x]
INORDER-TREE-WALK(right[x])

26. TREE-SEARCH (x, k)
if (x== NIL) || (k == key[x])
return x
if (k < key[x])
return TREE-SEARCH(left[x], k)
else
return TREE-SEARCH(right[x], k)

27. ITERATIVE-TREE-SEARCH(x, k)
while (x != NIL) && (k != key[x])
if k < key[x]
x = left[x]
else x = right[x]
return x

28. TREE-MINIMUM (x)
while left[x] != NIL
x = left[x]
return x
TREE-MAXIMUM(x)
while right[x] != NIL
x = right[x]
return x

29. TREE-SUCCESSOR(x)
if (right[x] != NIL)
return TREE-MINIMUM (right[x])
y = p[x]
while (y != NIL) && (x == right[y])
x = y
y = p[y]
return y

30. Insertion
• Proceed down the tree as you would with a find
• If X is found, do nothing (or update something)
• Otherwise, insert X at the last spot on the path
traversed
• Time complexity = O(height of the tree)

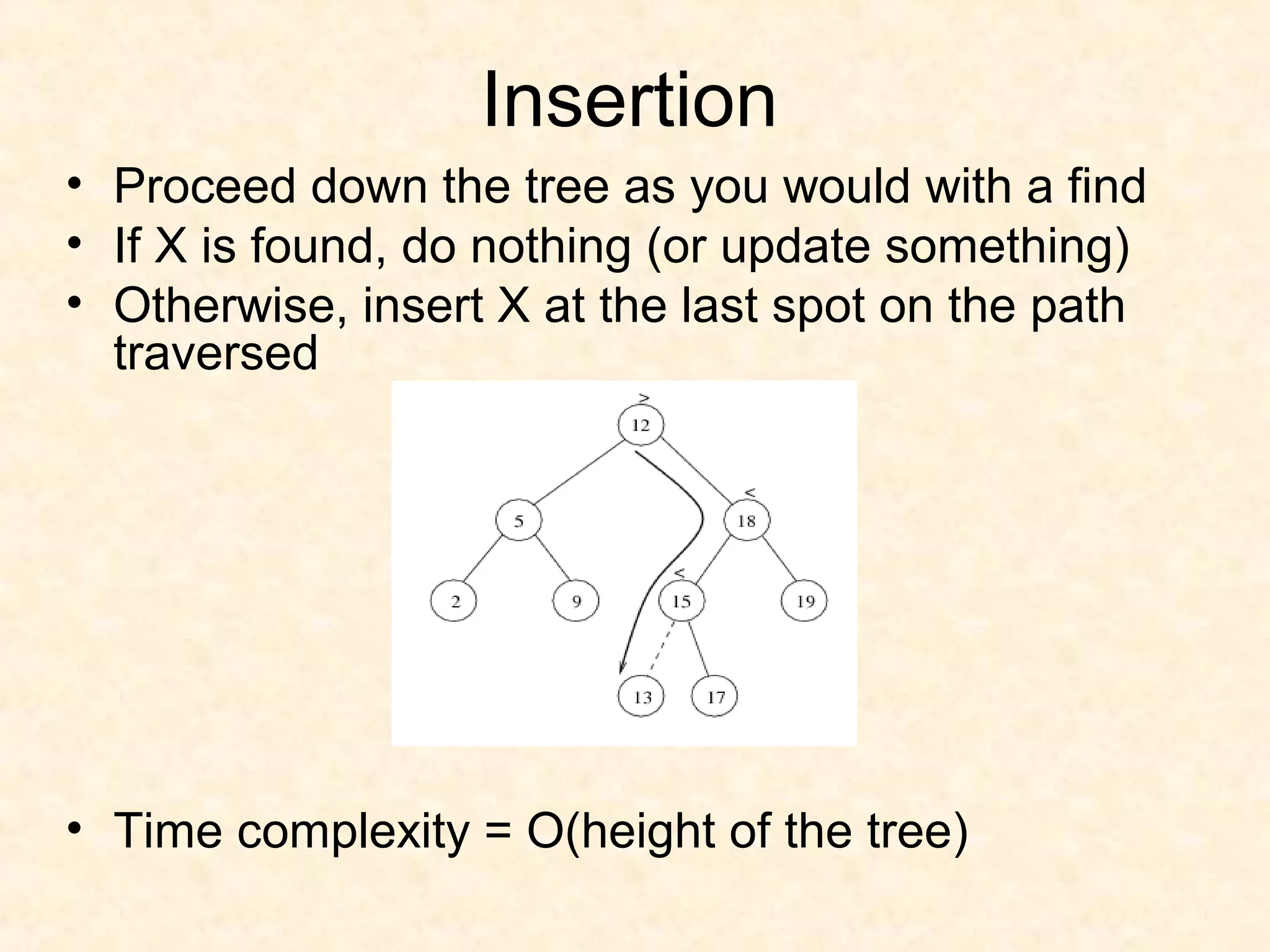
31. TREE-INSERT(T, z)
y = NIL
x = root[T]
while (x != NIL)
y = x
if (key[z] < key[x])
x = left[x]
else x = right[x]
p[z] = y
if (y == NIL)
root[T] = z // Tree T was empty
else if (key[z] < key[y])
left[y] = z
else right[y] = z

32. Deletion
• When we delete a node, we need to
consider how we take care of the children
of the deleted node.
– This has to be done such that the property of
the search tree is maintained.

33. Deletion under Different Cases
• Case 1: the node is a leaf
– Delete it immediately
• Case 2: the node has one child
– Adjust a pointer from the parent to bypass
that node

34. Deletion Case 3
• Case 3: the node has 2 children
– Replace the key of that node with the minimum
element at the right subtree
– Delete that minimum element
• Has either no child or only right child because if it has a
left child, that left child would be smaller and would have
been chosen. So invoke case 1 or 2.
• Time complexity = O(height of the tree)

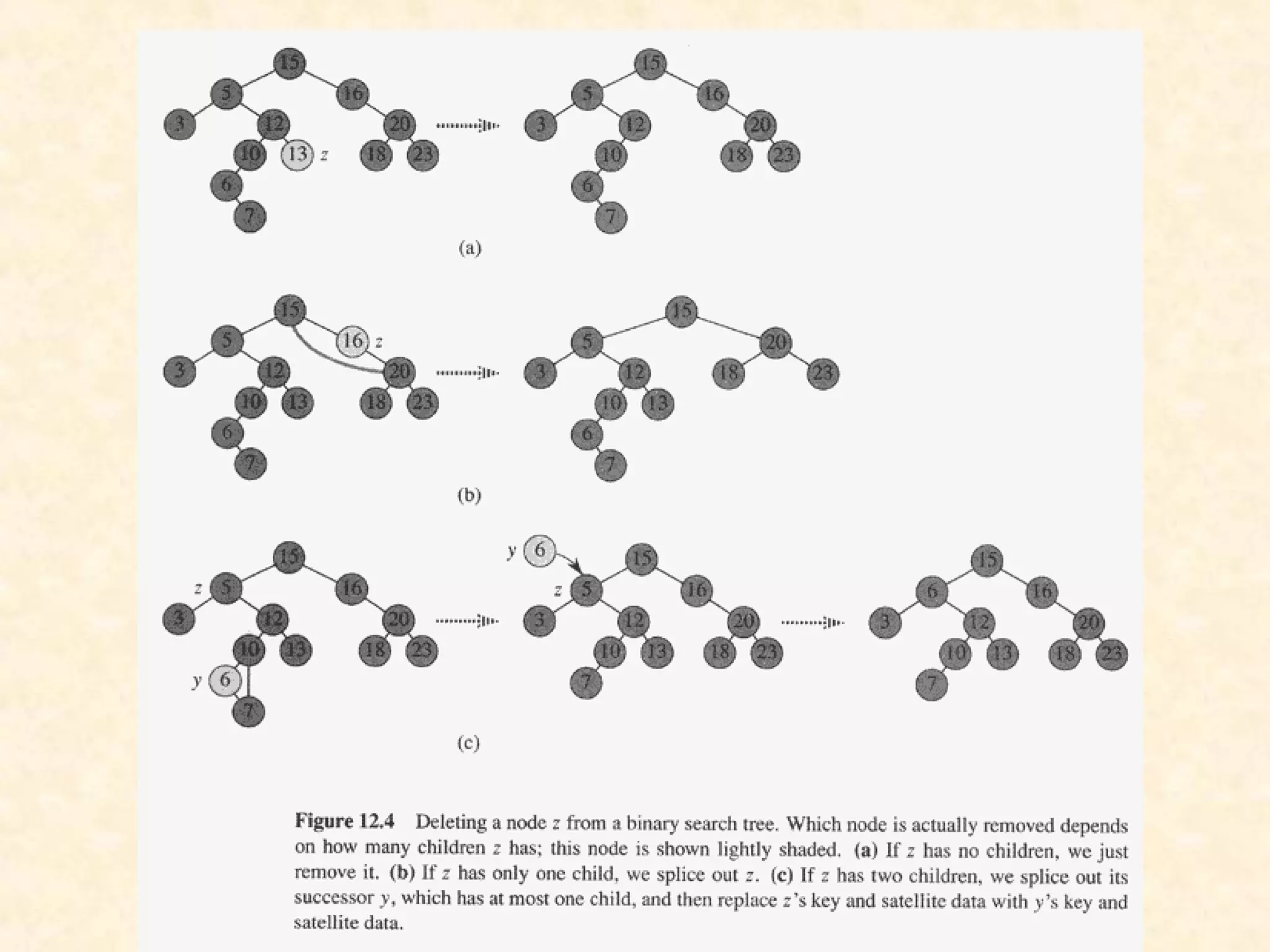
35. TREE-DELETE(T, z)
if (left[z] == NIL) || (right[z] == NIL)
y = z
else y = TREE-SUCCESSOR(z)
if (left[y] != NIL)
x = left[y]
else x = right[y]
if (x != NIL)
p[x] = p[y]
if (p[y] == NIL)
root[T] = x
else if (y == left[p[y]])
left[p[y]] = x
else right[p[y]] = x
if (y != z)
key[z] = key[y]
copy y's satellite data into z
return y

38. Threaded Binary Trees
• Too many null pointers in current
representation
of binary trees
n: number of nodes
number of non-null links: n-1
total links: 2n
null links: 2n-(n-1)=n+1
• Replace these null pointers with some useful
“threads”.

39. Threaded Binary Trees (Continued)
If ptr->left_child is null,
replace it with a pointer to the node that would be
visited before ptr in an inorder traversal
If ptr->right_child is null,
replace it with a pointer to the node that would be
visited after ptr in an inorder traversal

40. A Threaded Binary Tree
A
B C
GE
I
D
H
F
root
dangling
dangling
inorder traversal:
H, D, I, B, E, A, F, C, G

41. Element of the node
(inorder traversal only use
successor)
Left predecessor key successor rightLeft predecessor key successor right

42. Threaded Binary Trees
Given a binary tree with n nodes,
 the total number of links in the tree is 2n.
Each node (except the root) has exactly one incoming arc
 only n - 1 links point to nodes
 remaining n + 1 links are null.
One can use these null links to simplify some traversal processes.
A threaded binary search tree is a BST with unused links employed to
point to other tree nodes.
 Traversals (as well as other operations, such as backtracking)
made more efficient.
A BST can be threaded with respect to inorder, preorder or postorder
successors.

43. Threaded Binary Trees
Given the following BST, thread it to facilitate inorder traversal:
The first node visited in an inorder traversal is the leftmost leaf, node A.
Since A has no right child, the next node visited in this traversal is its
parent, node B.
Use the right pointer of node A as a thread to parent B to make backtracking
easy.
H
E
B
K
F J L
A D M
C
IG

44. Threaded Binary Trees
The thread from A to B is shown as the arrow in above diagram.
H
E
B
K
F J L
A D M
C
IG

45. Threaded Binary Trees
The next node visited is C, and since its right pointer is null, it also can be
used as a thread to its parent D:
H
E
B
K
F J L
A D M
C
IG

46. Threaded Binary Trees
Node D has a null right pointer which can be replaced with a pointer to D’s
inorder successor, node E:
H
E
B
K
F J L
A D M
C
IG

47. Threaded Binary Trees
The next node visited with a null right pointer is G. Replace the null pointer
with the address of G’s inorder successor: H
H
E
B
K
F J L
A D M
C
IG

48. Threaded Binary Trees
Finally, we replace:
first, the null right pointer of I with a pointer to its parent
and then, likewise, the null right pointer of J with a pointer to its parent
H
E
B
K
F J L
A D M
C
IG

49. Algorithm to right-thread BST
Perform an inorder traversal of the BST.
Whenever a node x with a null right pointer encountered
 replace this right link with a thread to the inorder successorof x.
If x is a left child of S then S is the inorder successor of x.
If x is not a left child, then the inorder successor S of x is
the nearest ancestor S of x that contains x in its left subtree.

50. Algorithm to right-thread BST
1. Initialize a pointer p to the root of the tree.
2. While (p) // p is not null:
a. While (p-> left) is not null,
p = p-> left.
b. Visit the node pointed to by p.
c. While p->right is a thread do:
i. p = p->right.
ii. Visit the node pointed to by p.
d. p = p->right.
Must be able to distinguish between right links that are threads and those
that are pointers to right children
 add a boolean field rightThread in the node declaration

51. Algorithm to right-thread BST
class BinNode
{
public:
DataType data;
bool rightThread;
BinNode *left,
*right;
BinNode ()
{
rightThread = false; // reset when tree threaded
left = right = 0;
}
BinNode (DataType item)
{
data = item;
rightThread = false; // reset when tree threaded
left = right = 0;
}
};// end of class BinNode declaration