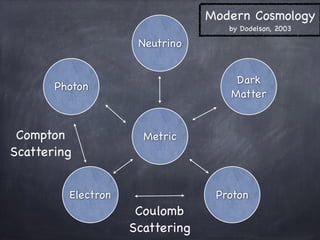
This document provides an outline for deriving the Boltzmann equation in cosmology. It begins with a brief introduction to modern cosmology and thermal physics. It then discusses the Boltzmann equation, describing its development by Ludwig Boltzmann. It proceeds to derive the photon Boltzmann equation in an expanding universe, considering terms for the expansion of the universe, curvature, and gravitational potential. Finally, it discusses using the Boltzmann equation to study the evolution of cosmic structure and perturbations to the distribution function, including compton scattering terms.

1. Boltzmann Equation in
Cosmology
Department of Physics, NTU
Jia-Long Yeh

2. Outline
Brief introduction of modern cosmology.
Derive Photon Boltzmann equation in
expanding Universe.
Compton Scattering
References

3. Cosmology
General Relativity
Thermal Physics

5. We can get lot in
thermal equilibrium
Saha’s equation -> when photon decouple
Entropy density -> reheating by massive particle
Nucleosynthesis

6. But…

7. We want to know more
about evolution of
cosmic structure

8. Boltzmann Equation

9. Ludwig Boltzmann
(1844-1906)

10. Neutrino
ProtonElectron
Photon
Dark
Matter
MetricCompton
Scattering
Coulomb
Scattering
Modern Cosmology
by Dodelson, 2003

11. Unit

12. The Boltzmann Equation
df
dt
= C[f]

13. Boltzmann equation
df
dt
=
@f
@t
+
@f
@xi
dxi
dt
+
@f
@p
dp
dt
+
@f
@ˆp
dˆp
dt
f
(0)
photon ⌘
1
e
p
T 1

14. Einstein Equation

15. Cosmological Principle
Isotropic
Homogeneous

16. Friedmann-Robertson-Walker
metric of Flat Universe
8
<
:
g00(~x, t) = 1
g0i(~x, t) = 0
gij(~x, t) = a(t)2
ij

17. Scalar perturbation in
Newtonian Gauge

18. Overdense region

19. Pµ
⌘
dxµ
d
P2
⌘ gµ⌫Pµ
P⌫ photon
= 0
P0
=
p
p
1 + 2
= p(1 )
P2
= (1 + 2 )(P0
)2
+ p2
= 0, p ⌘ gijPi
Pj
4-momentum

20. Pi
⌘ C ˆpi
C = p(1 )/a

21. dxi
dt
=
dxi
d
dt
d
=
Pi
P0
=
ˆpi
a
(1 + )
P0
= p(1 )
)
df
dt
=
@f
@t
+
@f
@xi
ˆpi
a
+
@f
@p
dp
dt

22. As the same token
1
p
dp
dt
= H
@
@t
ˆpi
a
@
@xi
1st-term: expansion of universe
2nd-term: curvature
3rd-term: gravitational potential

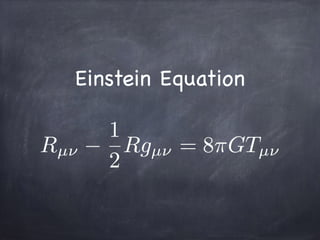
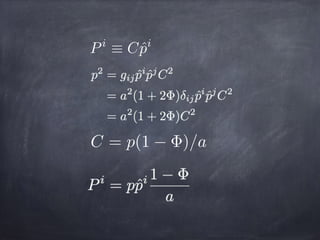
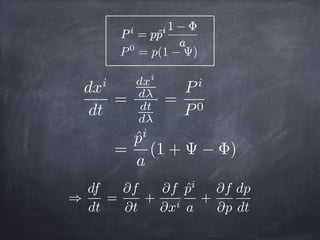
23. We get Boltzmann equation
)
df
dt
=
@f
@t
+
@f
@xi
ˆpi
a
@f
@p
p[H +
@
@t
+
ˆpi
a
@
@xi
]

24. Perturbed
Distribution Function
f = [exp{
p
T(1 + ⇥)
} 1] 1
'
1
ep/T 1
+ (
@
@T
[exp{
p
T
1}] 1
)T⇥
= f(0)
p
@f(0)
@p
⇥
Assume f = [exp{
p
T(1 + ⇥)
} 1] 1
f(0)
=
1
e
p
T 1
T
@f(0)
@T
= p
@f(0)
@p

25. Zero-Order
df
dt
=
@f(0)
@t
Hp
@f(0)
@p
= 0
@f(0)
@t
=
@f(0)
@T
dT
dt
=
dT/dt
T
p
@f(0)
@p
[
dT/dt
T
da/dt
a
]
@f(0)
@p
= 0
dT
T
=
da
a
) T /
1
a

26. Wavelength Stretch

27. C[f] for Compton Scattering
e (!q ) + (!p ) $ e (!q 0
) + (!p 0
)
C[f(!p )] =
X
!q ,!p 0,!p
| Amplitude |2
{fe(!q 0
)f(!p 0
) fe(!q )f(!p )}

28. First-Order
@⇥
@t
+
ˆpi
a
@⇥
@xi
+
@
@t
+
ˆpi
a
@
@xi
= ne T [⇥0 ⇥ + ˆp · !v b]
dt ⌘ ad⌘
µ ⌘
!
k · ˆp
k
˙⌧ ⌘
d⌧
d⌘
= ne T a
Fourier Transform
˙˜⇥ + ikµ˜⇥ + ˙˜ + ikµ˜ = ˙⌧[˜⇥0
˜⇥ + µ˜vb]

29. With Polarization

30. Notes
We only consider scalar mode
We only consider flat universe

31. Reference
Modern Cosmology
(Scott Dodelson, 2003)

32. Additional Reference
CMB anisotropies: Total angular momentum
method.
(Wayne Hu, Martin White, 1997, arxive:
astro-ph/9702170 )

33. Thanks