社内勉強会で『Python 機械学習プログラミング』の第 3 章の発表を担当した際の資料です。教科書で触れられている各アルゴリズムについて、アルゴリズムの概要と Iris データセットへの適用結果を説明しています。
発表資料に対応して、Jupyter Notebook で実行した ipynb ファイルを Gist にアップロードしています。
https://gist.github.com/y-uti/bd0928ad4f4eff7794a00108f6cbe7cc
[2017-05-08] スライド 37 ページの内容はカーネル SVM の理解について大きな誤りがあったため取り消します。




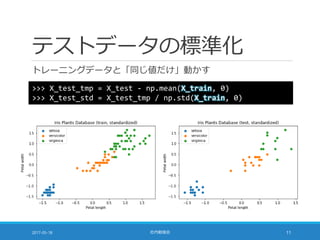
![層化抽出法
手持ちのデータは 3 品種それぞれ 50 サンプル
教科書の方法で分割すると各品種の比率は維持されない
2017-05-18 社内勉強会 8
>>> from collections import Counter
>>> sorted(Counter(y_train).items())
[(0, 34), (1, 32), (2, 39)]
層化抽出法:母集団の比率を維持してサンプリングする
◦ train_test_split 関数の stratify オプション
>>> X_train, ... = train_test_split(X, y, ..., stratify=y)
>>> sorted(Counter(y_train).items())
[(0, 35), (1, 35), (2, 35)]](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-8-320.jpg)

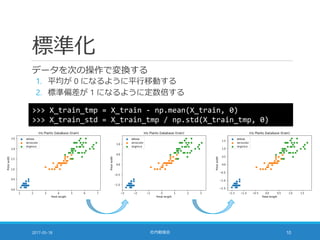



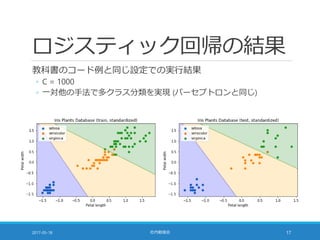
![ロジスティック回帰 [1/4]
例:virginica と「それ以外」を分類
まずは特徴量の重み付け和を考える (パーセプトロンと同じ)
2017-05-18 社内勉強会 18
z = 2.0 * petal_length - 1.5 * petal_width - 0.2](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-18-320.jpg)
![ロジスティック回帰 [2/4]
例:virginica と「それ以外」を分類
シグモイド関数を用いて 0 ~ 1 の範囲に押し込める
2017-05-18 社内勉強会 19
phi = 1.0 / (1.0 + np.exp(-z))](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-19-320.jpg)
![ロジスティック回帰 [3/4]
例:virginica と「それ以外」を分類
コスト関数 (= 分類のはずれ具合の総和) を考える
2017-05-18 社内勉強会 20
J = np.sum(-y * np.log(phi(z)) - (1-y) * np.log(1-phi(z)))
J = 59.78](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-20-320.jpg)
![ロジスティック回帰 [4/4]
例:virginica と「それ以外」を分類
コスト関数を小さくする方向に重みベクトルを更新する
2017-05-18 社内勉強会 21
z = 1.0 * petal_length + 1.0 * petal_width - 1.0
J = 27.94](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-21-320.jpg)

![コストパラメータ [1/2]
コスト関数 (= 分類のはずれ具合の総和) に掛ける係数
◦ 小さな値に設定 ⇒ 重みベクトルを小さくすること (正則化項) を重視
◦ 大きな値に設定 ⇒ 学習データを分類することを重視
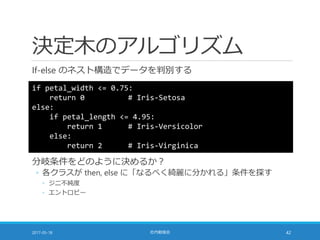
2017-05-18 社内勉強会 23](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-23-320.jpg)
![コストパラメータ [2/2]
ロジスティック回帰の場合
◦ 下図は petal length = petal width に沿って動かしたときの様子
◦ Versicolor (橙) は殆ど変化しない。他の分類器の影響で結果が変わる
2017-05-18 社内勉強会 24](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-24-320.jpg)

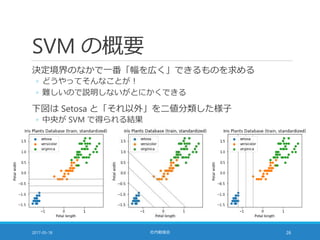
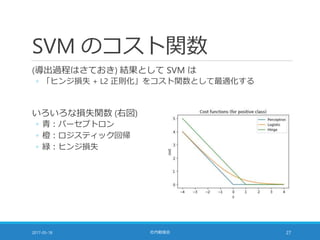
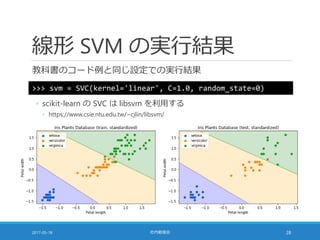
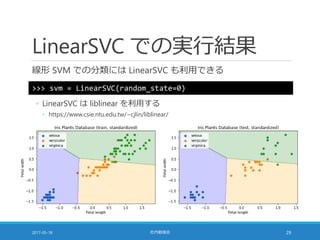


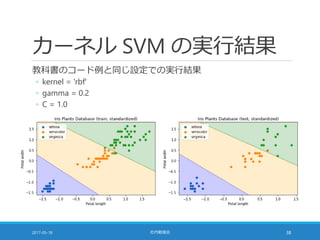
![カーネル SVM の威力 [1/4]
以下のようなデータを考える
◦ 左図:X と Y の符号が同じなら 0, 符号が異なっていたら 1
◦ 右図:原点からの距離の 2 乗が 2 未満なら 0, 2 以上なら 1
2017-05-18 社内勉強会 32](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-32-320.jpg)
![カーネル SVM の威力 [2/4]
このようなデータは線形分離不可能
◦ 下図は線形 SVM を適用して学習した結果
◦ まともに動かない
2017-05-18 社内勉強会 33](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-33-320.jpg)
![カーネル SVM の威力 [3/4]
カーネル SVM を適用する
◦ 下図は「二次の多項式カーネル」を用いて学習した結果
◦ なんだこれは!
2017-05-18 社内勉強会 34](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-34-320.jpg)
![カーネル SVM の威力 [4/4]
カーネル SVM を適用する
◦ 下図は「RBF カーネル」を用いて学習した結果
◦ なんだこれは!
2017-05-18 社内勉強会 35](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-35-320.jpg)
![カーネル SVM の概要 [1/2]
次の二つのアイデアの組み合わせ
1. 特徴量を「水増し」して高次元空間で線形分類する
2. 本当に水増しするのではなく「カーネル関数」で効率的に計算する
特徴量の水増し
◦ 元々の特徴量が 2 種類 (x1, x2) だったら・・・
◦ 2 次の項を追加すれば 5 種類
◦ x1*x1
◦ x1*x2
◦ x2*x2
◦ 3 次の項も追加すれば 9 種類
◦ x1*x1*x1
◦ x1*x1*x2
◦ x1*x2*x2
◦ x2*x2*x2
2017-05-18 社内勉強会 36
2 次の項を入れた 5 次元空間なら
これらはアッサリ分類できる](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-36-320.jpg)
![カーネル SVM の概要 [2/2]
次の二つのアイデアの組み合わせ
1. 特徴量を「水増し」して高次元空間で線形分類する
2. 本当に水増しするのではなく「カーネル関数」で効率的に計算する
カーネル関数
◦ 単純に特徴量を増やすと次元の数が爆発して実用にならない
◦ 重みベクトルとの内積さえ計算できればよい
例:2 次の多項式カーネル (本当はもう少し細かなパラメータがあります)
2017-05-18 社内勉強会 37
z = (1 + w1*x1 + w2*x2)^2
= 1 + 2 * w1 * x1
+ 2 * w2 * x2
+ w1*w1 * x1*x1
+ 2 * w1*w2 * x1*x2
+ w2*w2 * x2*x2
このスライドは色々と間違えています](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-37-320.jpg)
![gamma, C による変化 [1/2]
2017-05-18 社内勉強会 39](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-39-320.jpg)
![gamma, C による変化 [2/2]
2017-05-18 社内勉強会 40](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-40-320.jpg)
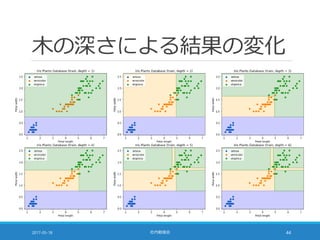
![エントロピー
情報理論の何やら難しい概念
◦ ここでは「各クラスのサンプルの混ざり具合い」だと思えばよい
2017-05-18 社内勉強会 45
def entropy(counts):
return np.sum([
-p * np.log2(p) if p > 0 else 0
for p in counts / np.sum(counts)])
>>> print(entropy([50, 50, 50])) # 1.58496250072
>>> print(entropy([20, 30, 50])) # 1.48547529723
>>> print(entropy([ 0, 30, 50])) # 0.954434002925
>>> print(entropy([ 0, 10, 50])) # 0.650022421648
>>> print(entropy([ 0, 0, 50])) # 0.0
◦ -p * log2(p) は p = 0 で計算不能だが +0 の極限が 0 なので 0 とする](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-45-320.jpg)
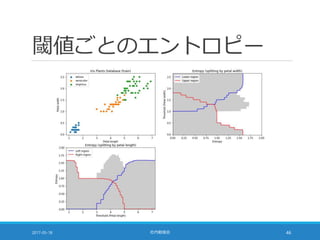
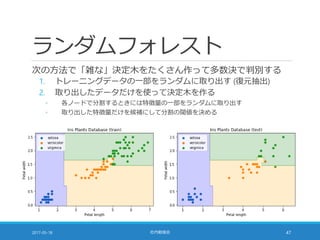
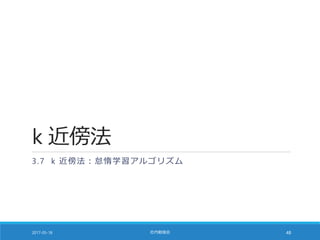
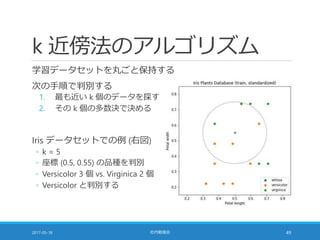
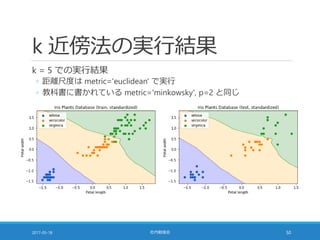
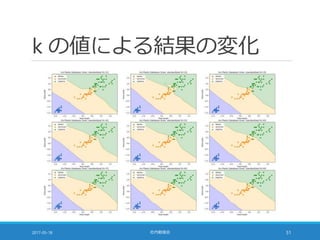
![多数決が同数の場合 [1/2]
scikit-learn の実装では「クラスの順序」に依存する
◦ scipy.stats.mode を利用しているため
◦ 教科書 91 ページの囲みの記述は誤り
参考
◦ scikit-learn の実装
◦ https://github.com/scikit-learn/scikit-learn/blob/0.18/sklearn/neighbors/classification.py
◦ scipy.stats.mode のドキュメント
◦ https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.stats.mode.html
weights='distance' パラメータ
◦ "weight points by the inverse of their distance"
◦ これは「多数決が同数の場合に距離が近いものを優先」ではない
2017-05-18 社内勉強会 52](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-52-320.jpg)
![多数決が同数の場合 [2/2]
人工的なデータに k 近傍法を適用した結果
2017-05-18 社内勉強会 53](https://image.slidesharecdn.com/20170518-pythonml-chapter3-170511153422/85/scikit-learn-53-320.jpg)

