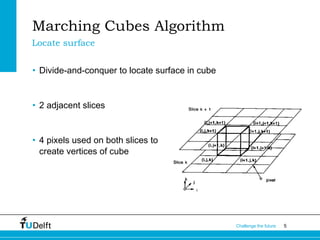
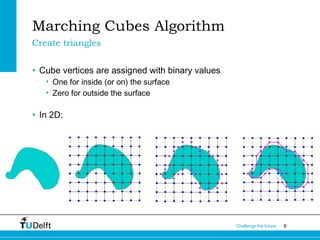
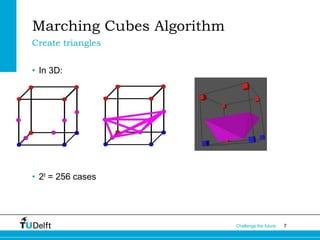
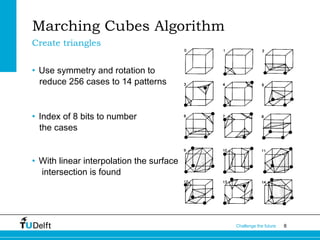
The document describes the Marching Cubes algorithm, which was developed in 1987 to construct 3D models from medical imaging data like CT scans. It works by dividing the volume into cubes and using the pixel values at the cube vertices to determine triangles that approximate the surface. There are 256 possible cases but they can be reduced to 14 basic patterns. The algorithm calculates surface normals to improve image quality and has been used to generate 3D models from various medical imaging modalities.

1. 1Challenge the future
Marching Cubes
A High Resolution 3D Surface Construction
Algorithm

2. 2Challenge the future
Introduction
• Algorithm developed by William E. Lorensen and Harvey E.
Cline and published in the 1987 SIGGRAPH proceedings.
• Aims to create 3D models from Medical data:
• X-ray computed tomography (CT)
• Magnetic resonance (MR)
• Single-photon emission computed
tomography (SPECT)

3. 3Challenge the future
3D Medical Algorithms & Related Work
Workflow:
1. Data acquisition: multiple 2D slices
2. Image processing to find structures or filter data
3. Surface construction
4. Display
Approaches:
• Contours of the surface on consecutive slices
connected with triangles
• Creates surfaces from cuberilles
• Octree, etc.

4. 4Challenge the future
Marching Cubes Algorithm
• Locate surface to a user-specified value
• Create triangles
• Calculate normals to ensure the quality of the image
Idea

5. 5Challenge the future
Marching Cubes Algorithm
• Divide-and-conquer to locate surface in cube
• 2 adjacent slices
• 4 pixels used on both slices to
create vertices of cube
Locate surface

6. 6Challenge the future
Marching Cubes Algorithm
• Cube vertices are assigned with binary values
• One for inside (or on) the surface
• Zero for outside the surface
• In 2D:
Create triangles

7. 7Challenge the future
Marching Cubes Algorithm
• In 3D:
• 28
= 256 cases
Create triangles

8. 8Challenge the future
Marching Cubes Algorithm
• Use symmetry and rotation to
reduce 256 cases to 14 patterns
• Index of 8 bits to number
the cases
• With linear interpolation the surface
intersection is found
Create triangles

9. 9Challenge the future
Marching Cubes Algorithm
• Final step to increase the quality of the image
• With central differences an unit normal can be calculated for
every cube vertex using 4 slices
• Interpolation of these normals
Calculate normals

10. 10Challenge the future
Improvements
• Efficiency increased by using pixel-to-pixel and line-to-line
coherence.
• 3 new edges are needed to interpolate
• Other 9 edges are obtained from previous slices, lines or pixels
• Reducing slice resolution by averaging four pixels into one
• Solid modeling using the three notions “inside”, “outside”,
and “on”

11. 11Challenge the future
Implementation and Results
Implementation
• Number of triangles is proportional to the area of the surface = A lot!
• Filtering is applied to reduce the resolution and number of triangles
Results
• CT
• MR
• SPECT

12. 12Challenge the future
Conclusions
• Realism is achieved by the calculation of the normalized gradient
• Large number of triangles reduced by surface cutting and
connectivity
• The algorithm has some flaws:
• high amount of memory needed to store resulting surface
• Sign change in the 14 original patterns can lead to mistakes