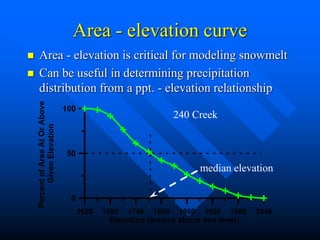
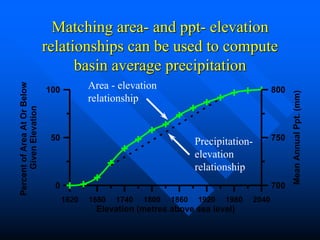
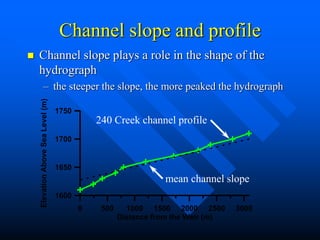
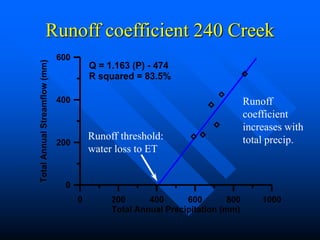
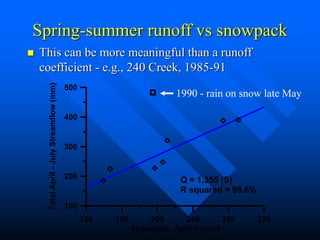
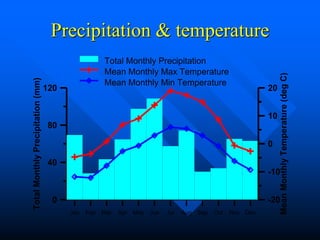
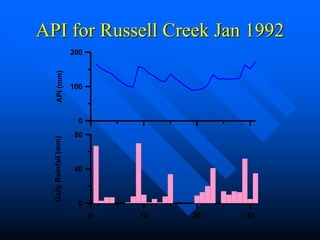
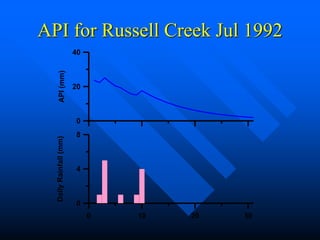
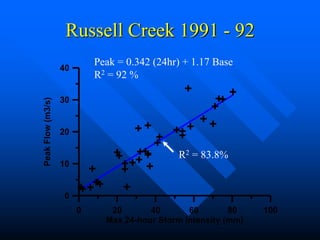
This document discusses factors that influence watershed morphology and the relationship between precipitation and runoff. It describes how watershed characteristics like basin size, land slope, drainage density and channel slope can affect the shape of a hydrograph. Larger basins with flatter slopes produce flatter hydrographs, while smaller, steeper basins produce more peaked hydrographs. It also examines methods for predicting runoff volumes and peak flows based on precipitation data, snowpack levels, and antecedent moisture conditions. Indices like the runoff coefficient, area-elevation curve, and antecedent precipitation index are used to quantify these relationships.

1. Basic Hydrology
Precipitation - Runoff Relations
Watershed Morphology

2. Watershed morphology
 Morphological properties of a watershed
can affect the shape of the storm
hydrograph and the delivery of sediment to
the main channel
 Various parameters can be calculated to
describe the channel network and the
physical characteristics of the watershed
– these all affect hydrograph shape

3. Basin size
 Delineate watershed according to the height
of land that separates water draining to the
point of interest from water that drains to
adjacent basins
 Watershed area (km2, ha)
– smaller watersheds tend to have a more peaked
hydrograph, more intermittent water supply
– larger watersheds have flatter hydrographs
because larger channel network can store more
water

4. Watershed land slope
 The slope of the sides of a watershed govern how
fast water will drain to the channel
– steep slopes - peaked hydrograph
– gentle slopes - flat hydrograph
 This is simply the average gradient of hillslopes -
slope is vertical over horizontal distance, derived
from topographic maps
 An objective repeatable formula for land slope:
S
L C I
A

( )( . .) where L is the total length of contours,
C.I. is the contour interval and A is the
watershed area.

5. Area - elevation curve
 Area - elevation is critical for modeling snowmelt
 Can be useful in determining precipitation
distribution from a ppt. - elevation relationship
1620 1680 1740 1800 1860 1920 1980 2040
Elevation (metres above sea level)
0
50
100
Percent
of
Area
At
Or
Above
Given
Elevation
240 Creek
median elevation

6. Matching area- and ppt- elevation
relationships can be used to compute
basin average precipitation
1620 1680 1740 1800 1860 1920 1980 2040
Elevation (metres above sea level)
0
50
100
Percent
of
Area
At
Or
Below
Given
Elevation
700
750
800
Mean
Annual
Ppt.
(mm)
Precipitation-
elevation
relationship
Area - elevation
relationship

7. Indices of basin shape
 Form factor
– elongated - F.F. is low, flatter hydrograph
– squatty - F.F. is high, peaked hydrograph
F F
Average Width
Axial Length
. .
.
.


8. Strahler’s order of streams
 A headwater stream with no
tributaries is a first order
stream
 When two first order
streams join they form a
second order stream
 Two second order streams
form a third order stream
 etc.
1
1
2
2
1
1 1
2 1
1
2
3
3
1

9. Bifurcation ratio
 Bi = ratio of # first order to # second order streams
 If watershed is > 2nd order:
1 2 3
Stream Order u
0.5
1.0
1.5
2.0
2.5
log
(#
Streams
of
Order
u)
log (Nu) = 2.77 -0.693 (u)
Plot log Nu vs. u as shown, Bi is the anti-log
of the slope of the regression line. For the
example given, Bi = anti-log(0.693) = 4.93

10. Effect of Bi on hydrograph shape
Elongated basin
Bi is high (=13)
flat hydrograph due to even
supply of water to channel
Rounder basin
Bi is low (= 4.9)
peaked hydrograph because
flow is concentrated
Assuming
uniform ppt.
distribution,
all other factors
being equal...

11. Channel slope and profile
 Channel slope plays a role in the shape of the
hydrograph
– the steeper the slope, the more peaked the hydrograph
0 500 1000 1500 2000 2500 3000
Distance from the Weir (m)
1600
1650
1700
1750
Elevation
Above
Sea
Level
(m)
240 Creek channel profile
mean channel slope

12. Determining mean channel slope
 Each tributary channel in a watershed has its own
profile
– commonly done only for the main channel
 Calculate the slope of a line drawn such that the
area under the line = the area under the main
channel profile
 An index of channel slope
can be calculated from the
slopes of n equal channel
segments:
S
s
n
c
i
i
n















1
2

13. Drainage density
 Drainage density is determined by
measuring the total length of all streams on
a map and dividing by the watershed area
– units of km/km2
– for comparative purposes, you must use maps
with the same level of detail for all basins of
interest
 Effect on hydrograph shape:
– high Dd - peaked hydrograph
– low Dd - flat hydrograph

14. Valley flat
 Area adjacent to stream or river floodplain
where the slope is < 8%
 Buffers the stream channel from landslides
which may run out on the valley flat before
depositing sediment in the channel.
 Calculate the length of mainstem channel
that has a valley flat, express as a proportion
of the length of the mainstem channel.

15. Other factors
 Lithology
– importance: can govern slope stability, bedrock
leakage, permeability
 Presence or absence of glaciers
– will govern timing and mangitude of peak
runoff
 Land use...

16. Precipitation - runoff
 Methods have been developed to predict
characteristics of runoff as a function of
precipitation characteristics
– volume of runoff
» seasonal
» annual
» based on seasonal or annual total precipitation
– peak flow
» annual peak flow - e.g., snowmelt peak (interior), a
function of peak snow accumulation
» storm peaks - a function of rainfall intensity

17. Runoff coefficient
 Simplest form of ppt - runoff relation
– ratio of total streamflow
over total precipitation
 Runoff coefficient can be assessed annually,
seasonally or monthly depending on
purpose
 Should be a characteristic quantity of a
watershed assuming no change in land use
R
Q
P


18. Calculating rainfall - runoff ratio
Example: 240 Creek, UPC
Water year Sept - Aug
Q P R
1987-88 236 640 0.37
1988-89 283 713 0.40
1989-90 522 859 0.61
1990-91 425 738 0.58
Since R is related to P or Q, a better way to get the ralationship
is to plot Q vs. P and fit a regression line.

19. Runoff coefficient 240 Creek
0 200 400 600 800 1000
Total Annual Precipitation (mm)
0
200
400
600
Total
Annual
Streamflow
(mm)
Q = 1.163 (P) - 474
R squared = 83.5%
Runoff threshold:
water loss to ET
Runoff
coefficient
increases with
total precip.

20. Spring-summer runoff vs snowpack
 This can be more meaningful than a runoff
coefficient - e.g., 240 Creek, 1985-91
120 160 200 240 280 320
Snowpack, April 1 (mm)
100
200
300
400
500
Total
April
-
July
Streamflow
(mm)
Q = 1.355 (S)
R squared = 99.6%
1990 - rain on snow late May

21. Predicting spring runoff in
interior watersheds
 Unlike runoff coefficient relationship, relationship
between spring - summer runoff and peak
snowpack passes through the origin
– this shows that virtually all the snowpack contributes to
spring - summer runoff
 Slope > 1: relationship is a very good predictor of
snowmelt runoff but doesn’t account for
precipitation that occurs after April 1 - doesn’t
work for unusual conditions such as rain-on-snow

22. Precipitation & temperature
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
0
40
80
120
Total
Monthly
Precipitation
(mm)
-20
-10
0
10
20
Mean
Monthly
Temperature
(deg
C)
Total Monthly Precipitation
Mean Monthly Max Temperature
Mean Monthly Min Temperature

23. Use of snow course data to
predict runoff
 For an interior watershed, snow course data should
provide a better measure of runoff
 Used to predict inflows to reservoirs, potential
floods
 For a coastal watershed, rainfall data is needed, but
annual runoff coefficient is probably relatively
meaningless
– monthly runoff ratio, averaged over several
years may be useful
– expected to be much higher than for interior w/s

24. Effect of antecedent conditions
on rainfall - runoff relation
 The amount of soil moisture prior to a storm will
affect the runoff ratio for that storm, and will affect
the shape of the hydrograph
– wet antecedent conditions lead to more runoff
per unit ppt., dry antecedent conditions result in
more of the input water going to basin recharge
– antecedent conditions are a function of ET and
soil/groundwater drainage.
 Not always possible to quantify these factors...

25. Antecedent Precipitation Index
 API is a method of accounting for daily
changes in water balance.
– API is a decay factor - each days API is a fixed
percentage of the previous day’s API (e.g.,
90%), plus daily rainfall and/or snowmelt
– runoff coefficient will vary according to the
API:
» the higher the API, the higher the runoff coefficient

26. API for Russell Creek Jan 1992
0 10 20 30
0
40
80
Daily
Rainfall
(mm)
0
100
200
API
(mm)

27. API for Russell Creek Jul 1992
0 10 20 30
0
4
8
Daily
Rainfall
(mm)
0
20
40
API
(mm)

28. Synthetic unit hydrograph
 It has been determined empirically that the
parameters of the unit hydrograph - lag
time, peak and time base - can be
determined from basin morphology
 lag time: (hours)
 
t C LL
p t C

0 3
.
LC
L = length of main
channel
Ct range 1.8 to 2.2

29.  Time base: (in days)
 Peak flow: various formulae have been
advanced to predict peak flow
– Rational formula: Qp = RIA
where R = runoff coefficient, I = rainfall
intensity and A = basin area
– Other formulae:
T
tp
 
3
3
24
Q
C A
t
p
p
p

Cp range 0.15 to 0.19 per mm
with Q in m3/s, A in km2

30. Russell Creek 1991 - 92
0 20 40 60 80 100
Max 24-hour Storm Intensity (mm)
0
10
20
30
40
Peak
Flow
(m3/s)
R2 = 83.8%
Peak = 0.342 (24hr) + 1.17 Base
R2 = 92 %