1. This document discusses the concepts of dot product, cross product, and work as they relate to vectors.
2. It provides formulas for calculating dot product, cross product, and work done by a force. Dot product is defined as the sum of the products of the corresponding components of two vectors and is a scalar.
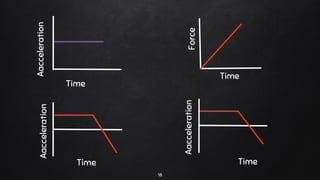
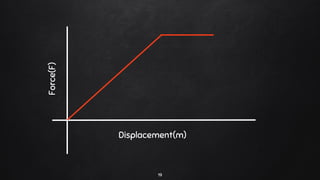
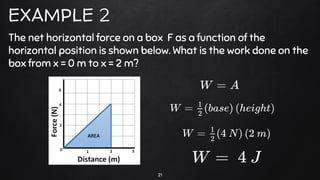
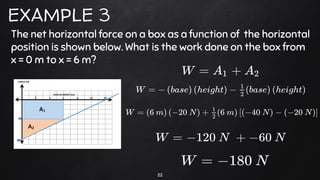
3. Several examples are worked out showing how to calculate the dot product, cross product, and work done in various situations involving forces and displacements. Work done is defined as the dot product of force and displacement vectors.





![CROSS PRODUCT
STEP 1: WRITE THE CROSS PRODUCT IN MATRIX FORMAT
STEP 2: WRITE THE COMPONENT USING THE DETERMINANT FROM THE STEP 1.
STEP 3: SIMPLIFY THE DETERMINANT
STEP 4: SIMPLIFY
𝐴⃑ × 𝐵⃑ =
𝑖 𝑗 𝑘
𝐴𝑥 𝐴𝑦 𝐴𝑧
𝐵𝑥 𝐵𝑦 𝐵𝑧
𝐴⃑ × 𝐵⃑ =
𝐴𝑦 𝐴𝑧
𝐵𝑦 𝐵𝑧
𝑖 −
𝐴𝑥 𝐴𝑧
𝐵𝑥 𝐵𝑧
j+
𝐴𝑥 𝐴𝑦
𝐵𝑥 𝐵𝑦
k
𝐴⃑ × 𝐵⃑ = [(𝐴𝑦𝐵𝑧 − 𝐴𝑧𝐵𝑦)𝑖̂ - (𝐴x𝐵z − 𝐴z𝐵x)𝑗̂ + (𝐴𝑥𝐵𝑦 − 𝐴𝑦𝐵𝑥)𝑘̂]](https://image.slidesharecdn.com/work-220420150043/85/WORK-pdf-6-320.jpg)
![EXAMPLE
𝐴⃑ = -2𝑖̂+ 4𝑗̂-7 𝑘̂
𝐵⃑ = -4𝑖̂+ 10𝑗̂+ 5𝑘̂
𝐴⃑ × 𝐵⃑ =
𝑖 𝑗 𝑘
−2 4 −7
−4 10 5
𝐴⃑ × 𝐵⃑ =
4 −7
10 5
𝑖 −
−2 −7
−4 5
j+
−2 4
−4 10
k
𝐴⃑ × 𝐵⃑ = [(4·5 − (-7)·10)𝑖̂ - (-2·5 − (-7)·(-4))𝑗̂ + (-2·10 − 4·(-4))𝑘̂]
𝐴⃑ × 𝐵⃑ = [(20+70)𝑖̂ - (-10-28)𝑗̂ + (-20+16)𝑘̂] = [90𝑖̂ ,38 𝑗̂ ,-4 𝑘̂]
𝐴⃑ × 𝐵⃑ =
𝑖 𝑗 𝑘
−2 4 −7
−4 10 5
𝐴⃑ × 𝐵⃑ =
𝑖 𝑗 𝑘
−2 4 −7
−4 10 5](https://image.slidesharecdn.com/work-220420150043/85/WORK-pdf-7-320.jpg)