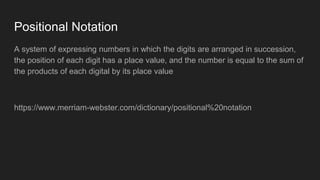
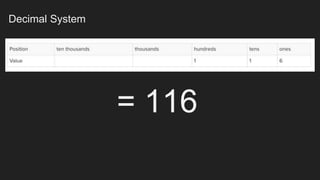
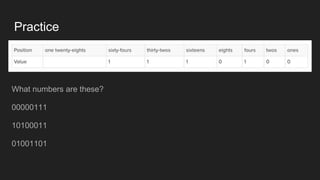
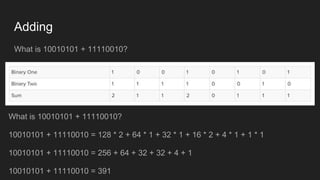
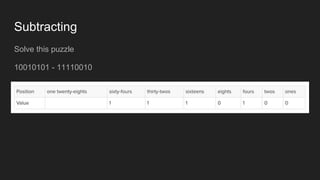
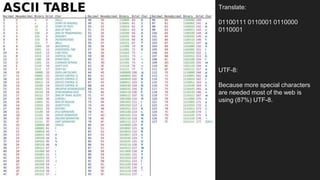
The document explains the concept of binary and decimal number systems, emphasizing that binary uses a base of 2 while decimal uses a base of 10. It provides examples of number conversions and operations in binary, including addition and subtraction, as well as practical applications in programming languages like JavaScript. Additionally, it mentions the widespread use of UTF-8 encoding for special characters on the web.