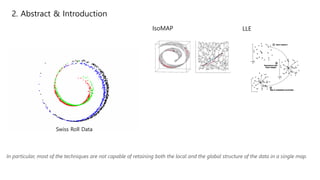
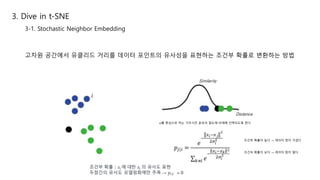
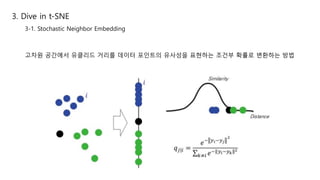
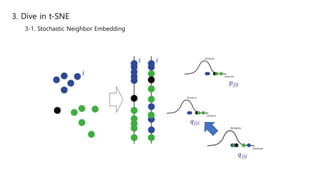
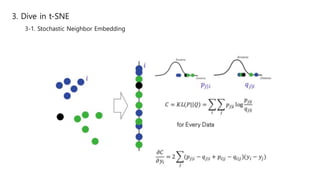
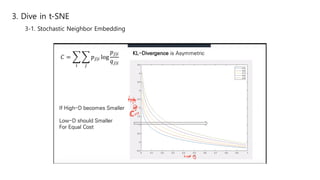
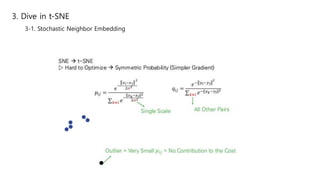
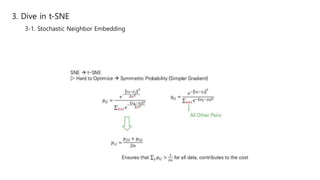
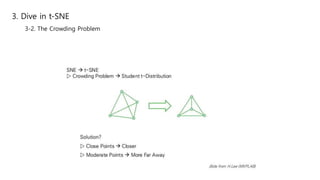
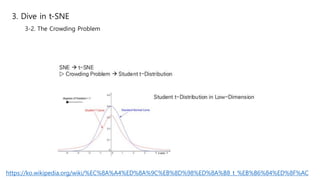
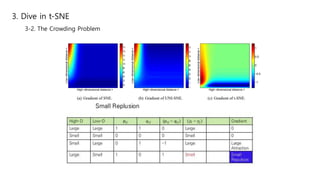
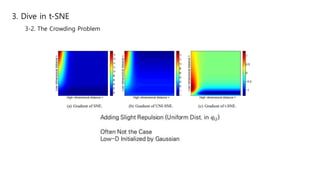
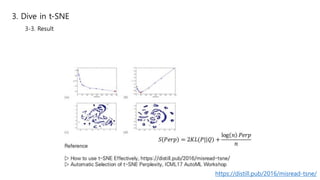
This document summarizes the t-SNE technique for visualizing high-dimensional data in two or three dimensions. It explains that t-SNE is an advanced version of Stochastic Neighbor Embedding (SNE) that can better preserve local and global data structures compared to linear dimensionality reduction methods. The document outlines how t-SNE converts Euclidean distances between data points in high-dimensions to conditional probabilities representing similarity. It also discusses the "crowding problem" that occurs when mapping high-dimensional data to low-dimensions, and how t-SNE addresses this issue.

1. Visualizing data using t-SNE
장경욱

2. Contents
2. Abstract & Introduction
3. Dive in t-SNE
1. Why I choose this paper?
3-1. Stochastic Neighbor Embedding
3-2. The Crowding Problem
3-3. Result

3. 1. Why I choose this paper?
http://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
Visualizing Data using t-SNE
시각화 공부
많은 자료
Creative AI
https://experiments.withgoogle.com/visualizing-high-dimensional-space

4. 2. Abstract & Introduction
t-SNE
Student T Distributed-Stochastic Neighbor Embedding
Nonlinear Dimension Reduction for Visualization (2-D or 3-D)
Advance Version of SNE (G. Hinton, NIPS 2003)
Gradient-based Machine Learning Algorithm

5. 2. Abstract & Introduction

6. 2. Abstract & Introduction

7. 2. Abstract & Introduction
고차원 데이터의 시각화는 다양한 분야에서 중요한 과제
- 다양한 차원 취급
- Ex : 유방암 관련 세포핵의 종류 – 30종류
- Ex : 문서를 표현하는 단어벡터 – 수천 차원

8. 2. Abstract & Introduction

9. 2. Abstract & Introduction

10. 2. Abstract & Introduction
Dimension Reduction Visualization
Traditional dimensionality reduction techniques such as
Principal Components Analysis (PCA; Hotelling, 1933)
classical multidimensional scaling (MDS; Torgerson, 1952) are
linear techniques that focus on keeping the low-dimensional
representations of dissimilar datapoints far apart
(1) Sammon mapping (Sammon, 1969),
(2) curvilinear components analysis (CCA; Demartines and Herault,1997),
(3) Stochastic Neighbor Embedding (SNE; Hinton and Roweis, 2002),
(4) Isomap (Tenenbaum et al., 2000),
(5) Maximum Variance Unfolding (MVU; Weinberger et al., 2004),
(6) Locally Linear Embedding (LLE; Roweis and Saul, 2000), and
(7) Laplacian Eigenmaps (Belkin and Niyogi, 2002)
https://docs.google.com/document/d/1gOMppfeYjoQFBqQjFXpEcHwWVXYRZF9EWjfxMPyj37Q/edit?usp=sharing

11. 2. Abstract & Introduction
History of Dimension Reduction
Linear
Principal Component Analysis (PCA) (1901)
Non - Linear
Multidimentional Scaling (MDS) (1964)
Sammon Mapping (1969)
IsoMap (2000)
Locally Linear Embedding (LLE) (2000)
Stochastic Neighbor Embedding (SNE) (2002)

12. 2. Abstract & Introduction

13. 2. Abstract & Introduction
IsoMAP LLE
In particular, most of the techniques are not capable of retaining both the local and the global structure of the data in a single map.
Swiss Roll Data

14. 2. Abstract & Introduction
Purpose
The aim of dimensionality reduction is
to preserve as much of the significant structure of the high-dimensional data
as possible in the low-dimensional map.

15. 2. Abstract & Introduction
Purpose
Local 구조 뿐만 아니라 Manifold를 유지하며 시각화 하겠다.
고차원 데이터
저차원 데이터

16. 2. Abstract & Introduction
+추가

17. 2. Abstract & Introduction
Problem

18. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding
고차원 공간에서 유클리드 거리를 데이터 포인트의 유사성을 표현하는 조건부 확률로 변환하는 방법
xi를 중심으로 하는 가우시안 분포의 밀도에 비례해 선택되도록 한다.
조건부 확률이 높다 → 데이터 점이 가깝다
조건부 확률이 낮다 → 데이터 점이 멀다

19. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding
고차원 공간에서 유클리드 거리를 데이터 포인트의 유사성을 표현하는 조건부 확률로 변환하는 방법

20. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

21. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

22. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

23. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

24. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

25. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

26. 3. Dive in t-SNE
3-1. Stochastic Neighbor Embedding

27. 3. Dive in t-SNE
3-2. The Crowding Problem

28. 3. Dive in t-SNE
3-2. The Crowding Problem
https://ko.wikipedia.org/wiki/%EC%8A%A4%ED%8A%9C%EB%8D%98%ED%8A%B8_t_%EB%B6%84%ED%8F%AC

29. 3. Dive in t-SNE
3-2. The Crowding Problem

30. 3. Dive in t-SNE
3-2. The Crowding Problem

31. 3. Dive in t-SNE
3-2. The Crowding Problem

32. 3. Dive in t-SNE
3-2. The Crowding Problem

33. 3. Dive in t-SNE
3-3. Result

34. 3. Dive in t-SNE
3-3. Result
https://distill.pub/2016/misread-tsne/

35. 3. Dive in t-SNE
3-3. Result

36. 3. Dive in t-SNE
3-3. Result

37. Reference
- http://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
- https://www.slideshare.net/TaeohKim4/pr-103-tsne
- https://www.slideshare.net/ssuser06e0c5/visualizing-data-using-tsne-73621033
- https://www.youtube.com/watch?v=zpJwm7f7EXs
- https://www.youtube.com/watch?v=NEaUSP4YerM
- https://ml-dnn.tistory.com/10
- http://mlexplained.com/2018/09/14/paper-dissected-visualizing-data-using-t-sne-
explained/
- https://lovit.github.io/nlp/representation/2018/09/28/tsne/
- https://lovit.github.io/nlp/representation/2018/09/28/mds_isomap_lle/