Downloaded 363 times
Uploaded byHitesh Sahu
Velocity triangles in Turbomachinery
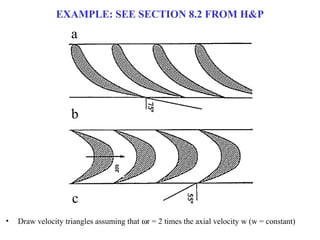
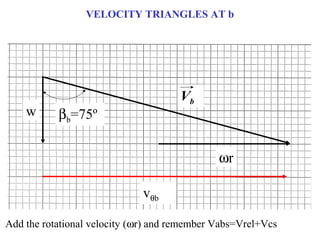
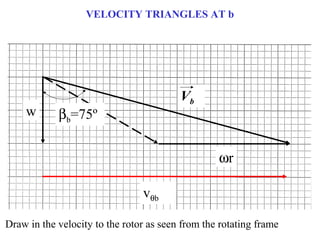
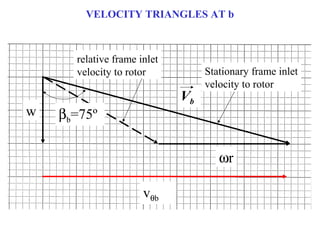
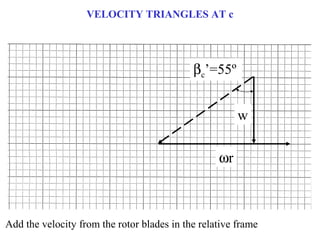
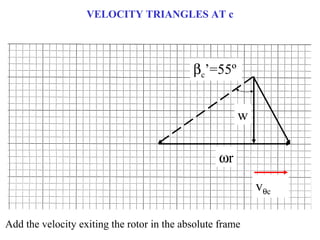
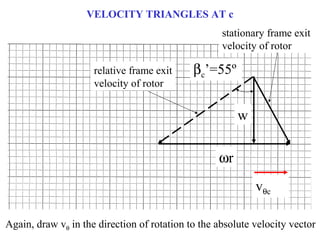
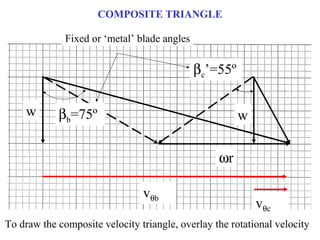
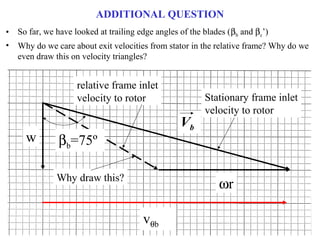
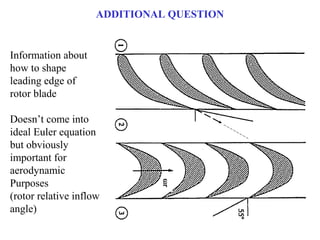
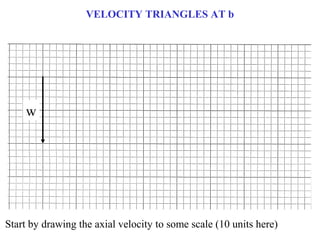
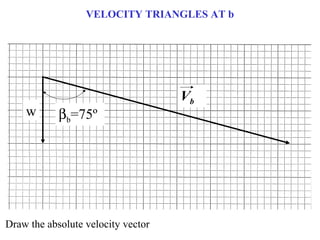
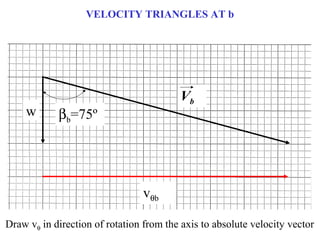
1) The document provides an example of using velocity triangles to analyze a turbine. It shows the velocity triangles drawn at two blade rows labeled b and c. 2) At each blade row, the axial, tangential, and absolute velocities are drawn to scale on the velocity triangle diagrams. This is done in both the stationary and relative frames. 3) The example calculates the torque applied to each blade row based on the change in angular momentum across it. It also describes the energy exchange process at each blade row, with kinetic energy being extracted from the flow by the moving blades.
More Related Content
Similar to Velocity triangles in Turbomachinery
Velocity triangles in Turbomachinery
- 1. Velocity Triangles Example VelocityTriangles Example April 12, 2012 Mechanical and Aerospace Engineering Department
- 2. EXAMPLE: SEE SECTION8.2 FROM H&P • Draw velocity triangles assuming that ωr = 2 times the axial velocity w (w = constant) a b c
- 3. VELOCITY TRIANGLES ATb w Start by drawing the axial velocity to some scale (10 units here)
- 4. VELOCITY TRIANGLES ATb w Vb βb=75º Draw the absolute velocity vector
- 5. VELOCITY TRIANGLES ATb w Vb βb=75º vθb Draw vθ in direction of rotation from the axis to absolute velocity vector
- 6. VELOCITY TRIANGLES ATb ωr w Vb βb=75º vθb Add the rotational velocity (ωr) and remember Vabs=Vrel+Vcs
- 7. VELOCITY TRIANGLES ATb ωr vθb w Vb βb=75º Draw in the velocity to the rotor as seen from the rotating frame
- 8. VELOCITY TRIANGLES ATb ωr vθb w Vb βb=75º Stationary frame inlet velocity to rotor relative frame inlet velocity to rotor
- 9. VELOCITY TRIANGLES ATc ωr Either start with the fixed axial velocity or fixed rotational speed
- 10. VELOCITY TRIANGLES ATc ωr βc’=55º w Add the velocity from the rotor blades in the relative frame
- 11. VELOCITY TRIANGLES ATc ωr βc’=55º w vθc Add the velocity exiting the rotor in the absolute frame
- 12. VELOCITY TRIANGLES ATc ωr βc’=55º w vθc relative frame exit velocity of rotor stationary frame exit velocity of rotor Again, draw vθ in the direction of rotation to the absolute velocity vector
- 13. COMPOSITE TRIANGLE ωr vθb w βb=75º βc’=55º vθc Todraw the composite velocity triangle, overlay the rotational velocity w Fixed or ‘metal’ blade angles
- 14. QUESTIONS • Is thisa compressor or a turbine? How can you tell? • On which blade row(s) is there a torque applied? Why? • Describe in words the energy exchange process in each of the two blade rows
- 15. QUESTIONS • Is thisa compressor or a turbine? – This is a turbine. The stationary frame tangential velocity (vθ) in the direction of rotor motion is reduced across the moving blade row • On which blade row(s) is there a torque applied? Why? – Torque is applied to both blade rows since there is a change in angular momentum across each of them. However, power is extracted only from the moving blades. • Describe in words the energy exchange process in each of the two blade rows – In the first blade row, fluid internal energy is converted to swirling kinetic energy by accelerating the flow through a nozzle. No additional energy is added or removed from the flow. – In the second blade row, swirling kinetic energy is extracted from the flow reducing the overall level of energy in the flow and transferring it to the spinning rotor blades. ( ) TP VVrmT inout ω θθ = −= ,,
- 16. ADDITIONAL QUESTION ωr vθb w Vb βb=75º Stationary frameinlet velocity to rotor relative frame inlet velocity to rotor • So far, we have looked at trailing edge angles of the blades (βb and βc’) • Why do we care about exit velocities from stator in the relative frame? Why do we even draw this on velocity triangles? Why draw this?
- 17. ADDITIONAL QUESTION Information about howto shape leading edge of rotor blade Doesn’t come into ideal Euler equation but obviously important for aerodynamic Purposes (rotor relative inflow angle)