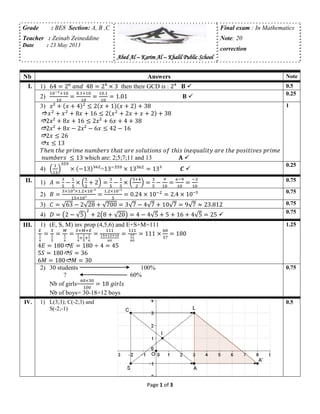
1) The student received a final exam in mathematics with 20 questions. Their total score was 60% or 12 out of 20 questions correct. 2) The exam covered topics like algebra, geometry, trigonometry, and statistics. Questions involved finding GCDs, simplifying expressions, solving inequalities, and calculating areas of shapes. 3) One statistics question asked them to calculate percentages based on a sample of 30 students where 60% liked a certain activity. They correctly found that 18 students would like the activity.

1. Page 1 of 3
Grade : BE8 Section: A, B ,C
Teacher : Zeinab Zeineddine
Date : 23 May 2013
Abed Al – Karim Al – Khalil Public School
Final exam : In Mathematics
Note: 20
correction
Nb Answers Note
I. 1) 64 = 26
𝑎𝑛𝑑 48 = 2⁴ × 3 then their GCD is : 2⁴ 𝐁  0.5
2)
10−1+10
10
=
0.1+10
10
=
10.1
10
= 1.01 𝐁  0.25
3) 𝑥² + (𝑥 + 4)2
≤ 2(𝑥 + 1)(𝑥 + 2) + 38
𝑥2
+ 𝑥2
+ 8𝑥 + 16 ≤ 2(𝑥2
+ 2𝑥 + 𝑥 + 2) + 38
2𝑥² + 8𝑥 + 16 ≤ 2𝑥² + 6𝑥 + 4 + 38
2𝑥² + 8𝑥 − 2𝑥² − 6𝑥 ≤ 42 − 16
2𝑥 ≤ 26
 𝑥 ≤ 13
𝑇ℎ𝑒𝑛 𝑡ℎ𝑒 𝑝𝑟𝑖𝑚𝑒 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑡ℎ𝑎𝑡 𝑎𝑟𝑒 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑜𝑓 𝑡ℎ𝑖𝑠 𝑖𝑛𝑒𝑞𝑢𝑎𝑙𝑖𝑡𝑦 𝑎𝑟𝑒 𝑡ℎ𝑒 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒𝑠 𝑝𝑟𝑖𝑚𝑒
𝑛𝑢𝑚𝑏𝑒𝑟𝑠 ≤ 13 which are: 2;5;7;11 and 13 𝐀 
1
4) (
1
13
)
359
× (−13)³⁶²=13−359
× 13362
= 13³ 𝑪 
0.25
II. 1) 𝐴 =
3
5
−
1
5
× (
5
2
+ 2) =
3
5
−
1
5
× (
5+4
2
) =
3
5
−
9
10
=
6−9
10
=
−3
10
0.75
2) 𝐵 =
3×10³×1.2×10⁻²
15×10³
=
1.2×10⁻²
5
= 0.24 × 10−2
= 2.4 × 10⁻³ 0.75
3) 𝐶 = √63 − 2√28 + √700 = 3√7 − 4√7 + 10√7 = 9√7 ≈ 23.812 0.75
4) 𝐷 = (2 − √5)
2
+ 2(8 + √20) = 4 − 4√5 + 5 + 16 + 4√5 = 25  0.75
III. 1) (E, S, M) inv prop (4,5,6) and E+S+M=111
𝐸
1
4
=
𝑆
1
5
=
𝑀
1
6
=
𝑆+𝑀+𝐸
1
4
+
1
5
+
1
6
=
111
15+12+10
60
=
111
37
60
= 111 ×
60
37
= 180
4𝐸 = 180 𝐸 = 180 ÷ 4 = 45
5𝑆 = 180 𝑆 = 36
6𝑀 = 180 𝑀 = 30
1.25
2) 30 students 100%
? 60%
Nb of girls=
60×30
100
= 18 𝑔𝑖𝑟𝑙𝑠
Nb of boys= 30-18=12 boys
0.75
IV. 1) L(3;3); C(-2;3) and
S(-2;-1)
0.5

2. Page 2 of 3
2) a. 𝑥𝐼 =
𝑥 𝑆+𝑥 𝐿
2
=
−2+3
2
=
1
2
and 𝑦𝐼 =
𝑦 𝑆+𝑦 𝐿
2
=
−1+3
2
= 1 0.5
b. A is the symmetric of C with respect to I  I  [AC]
𝑥𝐼 =
𝑥 𝐶+𝑥 𝐴
2

1
2
=
−2+𝑥 𝐴
2
 𝑥 𝐴 = 1 + 2 = 3
𝑦𝐼 =
𝑦 𝐶+𝑦 𝐴
2
1 =
3+𝑦 𝐴
2
 𝑦𝐴 = 2 − 3 = −1
0.5
c. ASCL is a rectangle: the diagonal bisect each other at I and 𝐴𝑆̂ 𝐶 = 90°
𝑃 = 2(𝐿 + 𝑊) = 2(4 + 5) = 18 𝑐𝑚
0.5
3) The image of CSA by vector 𝐶𝐿⃗⃗⃗⃗ is the triangle LAA’ and its right at A ( by translation)
𝐴 =
𝐴𝐿×𝐴𝐴′
2
=
4×5
2
= 10 𝑐𝑚²
0.5
V. 1) 𝑔(𝑥) = (4𝑥 + 1)² − 2(4𝑥 + 1)(𝑥 + 3) =16𝑥2
+ 8𝑥 + 1 − 2(4𝑥2
+ 12𝑥 + 𝑥 + 3)
= 16𝑥2
+ 8𝑥 + 1 − 8𝑥2
− 26𝑥 − 6
= 8𝑥² − 18𝑥 − 5
0.5
2) 𝑓(𝑥) = [(3𝑥 − 4) − (𝑥 + 5)][(3𝑥 − 4) + (𝑥 + 5)] = (2𝑥 − 9)(4𝑥 + 1)
𝑔(𝑥) = (4𝑥 + 1)[(4𝑥 + 1) − 2(𝑥 + 3)] = (4𝑥 + 1)(2𝑥 − 5)
1
3) 𝑓(𝑥) = 0(2𝑥 − 9)(4𝑥 + 1) = 0 𝑥 =
9
2
𝑜𝑟 𝑥 =
−1
4
0.5
4) a. 𝐴(𝑥) =
𝑓(𝑥)
𝑔(𝑥)
=
(2𝑥−9)(4𝑥+1)
(4𝑥+1)(2𝑥−5)
(4𝑥 + 1)(2𝑥 − 5)≠ 0 𝑥 ≠
−1
4
𝑎𝑛𝑑 𝑥 ≠
5
2
0.5
b. 𝐴(𝑥) =
(2𝑥−9)(4𝑥+1)
(4𝑥+1)(2𝑥−5)
=
2𝑥−9
2𝑥−5
=
2
3
3(2𝑥 − 9) = 2(2𝑥 − 5)
6𝑥 − 27 = 4𝑥 − 10
2𝑥 = 17 𝑥 =
17
2
0.5
VI.
𝐹𝑟𝑒𝑞 =
𝐴𝑛𝑔𝑙𝑒×𝑇
360°
%𝑅𝐹 =
𝐹𝑟𝑒𝑞
𝑇
× 100
Total=200 persons
1) Blue=(36° × 200) ÷ 360 = 20 𝑝𝑒𝑟𝑠𝑜𝑛𝑠
Black= 60 persons ; Green= 50 persons ; Brown= 70 persons
Colors Freq %RF
Black 60 30%
Brown 70 35%
Blue 20 10%
Green 50 25%
Total 200 100%
1.5

3. Page 3 of 3
2)
0.5
VII. C(0; 3cm) ; BC= 3 cm ; N [AC].
1) OC=OB= R= 3 cm and CB= 3 cm (given) then OCB is an equilateral ∆ 0.5
2) 𝐴𝐶̂ 𝐵 = 90° ( opposite to the diameter) and 𝐴𝐵̂ 𝐶 = 60° (equilateral ∆)
𝑡ℎ𝑒𝑛 𝐶𝐴̂ 𝐵 = 30° .
𝐴𝐵𝐶 𝑖𝑠 𝑎 𝑠𝑒𝑚𝑖 − 𝑒𝑞𝑢𝑖𝑙𝑎𝑡𝑒𝑟𝑎𝑙 ∆
1
3) AC=
𝐵𝐶√3
2
=
6√3
2
= 3√3 (𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑡ℎ𝑒 𝑎𝑛𝑔𝑙𝑒 60°)
In the ∆ ACB:
O[AB] By the midpoint th. ON=
𝐵𝐶
2
= 1.5 𝑐𝑚 and (ON) // (BC)
N [AC]
1
4) In the triangle AMB we have:
𝐵̂ = 90° 𝑎𝑛𝑑 𝑀𝐴̂ 𝐵 = 30° then AMB is a semi equilateral ∆
𝐴𝐵 =
𝐴𝑀√3
2
 6=
𝐴𝑀√3
2
 𝐴𝑀 =
12
√3
= 4√3
BM=
𝐴𝑀
2
= 2√3
1
5) 𝐴 𝐶𝑂𝐵 =
𝜋𝑅²×𝐶𝑂̂ 𝐵
360°
=
𝜋×9×60
360
=
3𝜋
2
𝑐𝑚² 1
6) 𝐴𝑁̂ 𝑂 = 𝐴𝐶̂ 𝐵 = 90° ( corresponding angles)
𝐴 𝑎𝑛𝑑 𝑂 𝑎𝑟𝑒 𝑓𝑖𝑥𝑒𝑑 𝑝𝑜𝑖𝑛𝑡𝑠 𝑡ℎ𝑒𝑛 𝑁 𝑏𝑒𝑙𝑜𝑛𝑔𝑠 𝑡𝑜 𝑎 𝑐𝑖𝑟𝑐𝑙𝑒 𝑜𝑓 𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟 [𝐴𝑂]
1
60
70
20
50
0
10
20
30
40
50
60
70
80
Black Brown Blue Green
Bar graph
Freq