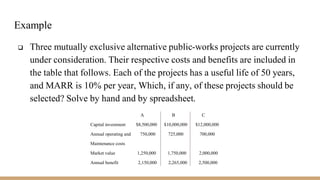
The document discusses the benefit-cost ratio method for evaluating public projects. It provides definitions for different types of public projects like self-liquidating and multiple-purpose projects. It then outlines the difficulties in evaluating public projects and introduces the benefit-cost ratio method. The key steps to calculate the conventional and modified benefit-cost ratio are presented. The document also discusses how to use the benefit-cost ratio method to evaluate mutually exclusive projects and provides an example of incremental benefit-cost analysis for projects with unequal lives.

1. BENEFIT-COST RAITO METHOD
PROJECT MEMBERS:
• Bijeta Rijal
• Giriraj Timilsina
• Kiran khatri
• Kushal Bhatta
• Nischal Bhattarai
SUBMITTED TO:
 Rudra p. Ghimire

2. Table of Contents
• PUBLIC PROJECTS
• DIFFICTLTIES IN EVALUATING
• INTRODUCTION TO B-C RATIO METHOD
• MUTUALLY EXCLUSIVE PROJECTS
• COMPARISION OF MUTUALLY EXCLUSIVE PROJECTS BY B-C RATIO METHOD

3. PUBLIC PROJECTS
• Authorized, Financed and Operated by government agencies.
• Much larger than private ventures and need huge capital.
• Relatively long project life (20-60 years).
• Mainly service oriented.
• Significant effect of politics.

4. SELF LIQUIDATING PROJECTS
• Public projects expected to earn direct revenue and repay its cost.
• Not expected to make a profit or pay taxes.
• Examples are toll bridges, highways, irrigation water, fresh water,
electric power, etc.

5. MULTIPLE-PURPOSE PROJECTS
• Most of the public projects are multi-purposed.
• Multiple-purpose projects like a dam to create a reservoir in a river may
have the following objectives:
i. Assist flood control.
ii. Provide drinking water.
iii. Generate electric power.
iv. Provide water for irrigation.

6. DIFFICULTIES IN EVALUATING
• Difficult in cost division due to multiple purposes.
• Monetary impacts due to the project are difficult to quantify.
• No profit standard to measure financial effectiveness.
• Very less connection between the project and its real owner.
• Huge political influence.

7. INTRODUCTION TO B-C RATIO
METHOD
• It is the ratio of equivalent worth of benefits to the costs generally
used to choose alternatives.
• This method is majorly used in public project.
• Time value of money must be consider to account for timing of cash
flow.
• B-C ratio is also called as the savings- investment ratio(SIR).

8. Contd….
There are two ways to calculate B-C:
1. Conventional B-C ratio with
PW(&AW):
2. Modified B-C ratio with PW(&AW);

9. 1. Conventional B-C ratio with PW:
B-C= PW(benefits of the proposed project)
PW(total costs of the proposed project)
= PW(B)
I-PW(MV)+PW(O&M)
Where,
PW(.)= present worth of (.);
B=benefits of the proposed project;
I=initial investment in the proposed project;
MV=market value at the end of useful life;
O&M=operating and maintenance costs of the proposed
project

10. WITH AW:
B-C= AW(B)
CR+AW(O&M)
Where,
AW(.)=annual worth of (.);
CR= capital recovery(i.e. I-PW(MV)

11. 2. MODIFIED B-C RATIO WITH PW:
B-C= PW(B) - PW(O&M)
I - PW(MV)
• A project is accepted if the B-C ratio is greater than or equal to 1.

12. With AW:
B-C=AW(B) - AW(O&M)
CR
HERE , AW stands for annual worth

13. EXAMPLE:
The city of Columbia is considering extending the runways of its
municipal airport so that commercial jets can use the facility. The land
necessary for the runway extension is currently a farmland that can be
purchased for $350,000. Construction costs for the runway extension
are projected to be $600,000, and the additional annual maintenance
costs for the extension are estimated to be $22,500. If the runways are
extended, a small terminal will be constructed at a cost of $250,000. The
annual operating and maintenance costs for the terminal are estimated at
$75,000. Finally, the projected increase in flights 454 CHAPTER 10 /
EVALUATING PROJECTS WITH THE BENEFIT–COST RATIO
METHOD will require the addition of two air traffic controllers at an
annual cost of $100,000.

14. Annual benefits of the runway extension have been estimated as
follows: $325,000 Rental receipts from airlines leasing space at
the facility $65,000 Airport tax charged to passengers $50,000
Convenience benefit for residents of Columbia $50,000
Additional tourism dollars for Columbia Apply the B–C ratio
method with a study period of 20 years and a MARR of 10% per
year to determine whether the runways at Columbia Municipal
Airport should be extended

15. Solution
Conventional B–C:
B–C = PW(B)/[I − PW(MV) + PW(O&M
B–C = $490,000 (P/A, 10%, 20)/[$1,200,000 + $197,500
(P/A, 10%, 20)] B–C = 1.448 > 1; extend runways.
Modified B–C:
B–C = [PW(B) − PW(O&M)]/[I − PW(MV)]
B–C = [$490,000 (P/A, 10%, 20) − $197,500 (P/A, 10%,
20)]/$1,200,000 B–C = 2.075 > 1; extend runways.
.

16. Conventional B–C:
B–C = AW(B)/[CR + AW(O&M)]
B–C = $490,000/[$1,200,000 (A/P, 10%, 20) + $197,500]
B–C = 1.448 > 1; extend runways.
Modified B–C:
B–C = [AW(B) − AW(O&M)]/CR B–C
= [$490,000 − $197,500]/[$1,200,000 (A/P, 10%, 20)]
B–C = 2.075 > 1; extend runways

17. MUTUALLY EXCLUSIVE PROJECTS
● Mutually Exclusive refers to the events which cannot happen at the same
particular time. Ex: either head or tail when tossing a coin.
● Mutually Exclusive Projects is defined as a group of projects from which
at most, one project may be selected.
● A project is selected on the basis of certain parameter that includes
operation and management cost, profit from the application of project,
investment, etc.
● Acceptance of one project results in rejection of all the other projects.

18. COMPARISION OF MUTUALLY EXCLUSIVE
PROJECTS BY B-C RATIO METHOD
● Mutually Exclusive Project are compared by Benefit-Cost Ratio i.e, B-C
ratio as it provides a ratio of benefits to costs rather than just the profit
potential.
● For the selection of the project by B-C ratio, the alternative with the B-C
ratio greater or equal to 1 is accepted while the other alternative with B-C
ratio less than 1 is rejected .
● Best alternative can be selected using an equivalent.worth method by
maximizing the PW or Aw or FW.

19. Contd……
● The evaluation of the mutually exclusive project by B-C ratio is
conducted improperly by equivalent worth method which includes
convenient and modified B-C (as mentioned earlier).
● Therefore a comparison of mutually exclusive alternatives require an
incremental analysis to be conducted.

20. INCREMENTAL B-C ANALYSIS OF MUTUALLY
EXCLUSIVE PROJECTS
Process for the calculation of mutually exclusive project by incremental
analysis is as follows:
● When comparing mutually exclusive alternatives with B-C ratio method,
they are first ranked in order of increasing total equivalent worth of costs.
● This rank ordering will be identical whether the ranking is based on PW,
AW or FW of costs.
● Projects are ranked from smallest to largest according to costs obtained.
● The project with smallest cost is calculated for alternative.

21. Contd…..
● The b-c ratio of that particular project is calculated and if it is greater or equal to
1, it is regarded as the baseline alternative, otherwise we carry the process by
calculating b-c ratio of the following project.
● Then the following larger project is selected, the difference in the respective
benefits and costs of this project and baseline is used to calculate incremental b-
c ratio.
● If this project has b-c ratio greater or equal to 1 then this is set as new baseline
alternative , otherwise the last baseline is maintained.
● Similarly the process of calculating b-c ratio with incremental analysis is
followed until the last project is compared.

22. Example
 Three mutually exclusive alternative public-works projects are currently
under consideration. Their respective costs and benefits are included in
the table that follows. Each of the projects has a useful life of 50 years,
and MARR is 10% per year, Which, if any, of these projects should be
selected? Solve by hand and by spreadsheet.
A B C
Capital investment $8,500,000 $10,000,000 $12,000,000
Annual operating and 750,000 725,000 700,000
Maintenance costs
Market value 1,250,000 1,750,000 2,000,000
Annual benefit 2,150,000 2,265,000 2,500,000

23. Contd…..
 Solution
PW(Costs, A) = $8,500,000 + $750,000(P/A, 10%, 50) − $1,250,000(P/F, 10%, 50) = $15,925,463,
PW(Costs, B) = $10,000,000 + $725,000(P/A, 10%, 50) − $1,750,000(P/F, 10%, 50) = $17,173,333,
PW(Costs, C) = $12,000,000 + $700,000(P/A, 10%, 50) − $2,000,000(P/F, 10%, 50) = $18,923,333,
PW(Benefit, A) = $2,150,000(P/A, 10%, 50) = $21,316,851,
PW(Benefit, B) = $2,265,000(P/A, 10%, 50) = $22,457,055,
PW(Benefit, C) = $2,500,000(P/A, 10%, 50) = $24,787,036.
B–C(A) = $21,316,851/$15,925,463
= 1.3385 > 1.0.
Therefore, Project A is acceptable.
ΔB/ΔC of (B − A) = ($22,457,055 − $21,316,851)/($17,173,333 − $15,925,463)
= 0.9137 < 1.0.
Therefore, increment required for Project B is not acceptable.
ΔB/Δ C of (C − A) = ($24,787,036 − $21,316,851)/($18,923,333 − $15,925,463)
= 1.1576 > 1.0.
Therefore, increment required for Project C is acceptable

24. B-C ANALYSIS WITH UNEQUAL PROJECTS LIVES
● In mutually exclusive projects there are some project that have different
lives.
● The projects with varying useful lives is also possible to conduct an
incremental B-C analysis by using the AW of benefits and costs of the
various projects.
● Process includes calculating AW for each project. The following process
is same as for the mutually exclusive project with same lives.

25. Example
 Two mutually exclusive alternative public-works projects are under
consideration. Their respective costs and benefits are included in the table
that follows. Project I has an anticipated life of 35 years, and the useful
life of Project II has been estimated to be 25 years. If the MARR is 9% per
year, which, if either, of these projects should be selected? The effect of
inflation is negligible.
Project I Project II
Capital investment $750,000 $625,000
Annual operating and maintenance 120,000 110,000
Annual benefit 245,000 230,000
Useful life of project (years) 35 25

26. Contd…..
 Solution
AW(Costs, I) = $750,000(A/P, 9%, 35) + $120,000 = $190,977,
AW(Costs, II) = $625,000(A/P, 9%, 25) + $110,000 = $173,629,
B–C(II) = $230,000/$173,629 = 1.3247 > 1.0.
Therefore, Project II is acceptable.
ΔB/ΔC of (I–II) = ($245,000 − $230,000)/($190,977 − $173,629)
= 0.8647 < 1.0.
Therefore, increment required for Project I is not acceptable hence Project II should be selected.