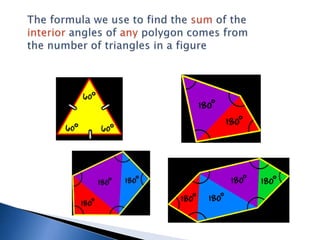
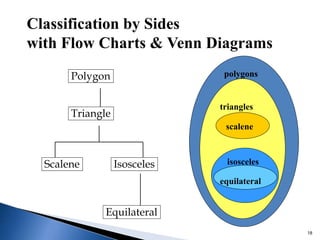
The document defines and classifies different types of quadrilaterals. It discusses properties of parallelograms, trapezoids, kites, and other quadrilaterals. Key types include parallelograms, which have two pairs of parallel sides, and trapezoids, which have one set of parallel sides. A square is defined as a special type of rectangle with four equal sides and four right angles. The document also discusses classifications of quadrilaterals based on angles and sides.

2.  A plane figure bounded by four line
segments AB,BC,CD and DA is called
a quadrilateral.
A B
D C

3. In geometry, a quadrilateral is a polygon with four
sides and four vertices. Sometimes, the term
quadrangle is used, for etymological symmetry with
triangle, and sometimes tetragon for consistence with
pentagon.
There are over 9,000,000 quadrilaterals.
Quadrilaterals are either simple (not self-intersecting)
or complex (self-intersecting). Simple quadrilaterals
are either convex or concave.

4.  Parallelogram
 Trapezium
 Kite

6. 6
These figures are not polygons These figures are polygons
Definition:A closed figure formed by line segments so that each
segment intersects exactly two others, but only at their
endpoints.

7. 7
Convex: No line containing a side of the polygon contains a point
in its interior
Concave:
A polygon for which there is a line
containing a side of the polygon and
a point in the interior of the polygon.

8. 8
Regular: A convex polygon in which all interior angles have the
same measure and all sides are the same length
Irregular:Two sides (or two interior angles) are not congruent.

9. 9
3 sides Triangle
4 sides
5 sides
6 sides
7 sides
8 sides
Nonagon
Octagon
Heptagon
Hexagon
Pentagon
Quadrilateral
10 sides
9 sides
12 sides
Decagon
Dodecagon
n sides n-gon

18. 18
polygons
Classification by Sides
with Flow Charts & Venn Diagrams
triangles
Scalene
Equilateral
Isosceles
Triangle
Polygon
scalene
isosceles
equilateral

19. 19
polygons
Classification by Angles
with Flow Charts & Venn Diagrams
triangles
Right
Equiangular
Acute
Triangle
Polygon
right
acute
equiangular
Obtuse
obtuse

20. • 2 sets of parallel sides
• 2 sets of equal sides
• Opposite angles equal
• Adjacent angles supplementary
• Diagonals bisect each other
• Diagonals form 2 congruent triangles
Parallelogram

21. Types of Parallelograms
*Rectangle
I have all of the properties of the
parallelogram PLUS
- 4 right angles
- diagonals congruent

22. *Rhombus
I have all of the properties of the
parallelogram PLUS
- 4 congruent sides
- diagonals bisect angles
- diagonals perpendicular

23. *Square
Hey, look at me!
I have all of the properties of the
parallelogram AND the rectangle AND
the rhombus.
I have it all!

24. Is a square a rectangle?
• Some people define categories exclusively, so
that a rectangle is a quadrilateral with four right
angles that is not a square.
• This is appropriate for everyday use of the words,
as people typically use the less specific word only
when the more specific word will not do.
• Generally a rectangle which isn't a square is an
oblong.

25. • But in mathematics, it is important to define
categories inclusively, so that a square is a
rectangle.
• Inclusive categories make statements of
theorems shorter, by eliminating the need for
tedious listing of cases.
• For example, the visual proof that vector
addition is commutative is known as the
"parallelogram diagram".
• If categories were exclusive it would have to
be known as the "parallelogram (or rectangle
or rhombus or square) diagram"!

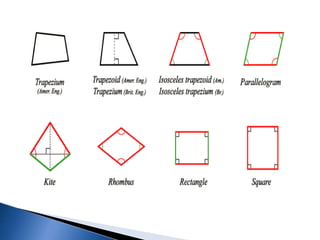
26. Trapezium
I have only one set of parallel sides.
[The median of a trapezium is parallel to the
bases and equal to one-half the sum of the
bases.]
Trapezoid Regular Trapezoid

27. • It has two pairs of sides.
Each pair is made up of adjacent sides (the
sides meet) that are equal in length.
• The angles are equal where the pairs meet.
• Diagonals (dashed lines) meet at a right
angle, and one of the diagonal bisects
(cuts equally in half) the other.
Kite

28. Cyclic quadrilateral: the four
vertices lie on a circumscribed
circle.
Tangential quadrilateral: the four
edges are tangential to an inscribed
circle. Another term for a tangential
polygon is inscriptible.
Bicentric quadrilateral: both cyclic
and tangential.
Some other types of
quadrilaterals

29. The sum of all four angles of a quadrilateral is 360
.
.
A
B C
D
1
2
3
4
6
5
Given: ABCD is a quadrilateral
To Prove: Angle (A+B+C+D) =360
.
Construction: Join diagonal BD

30. Thank you
for your
attention