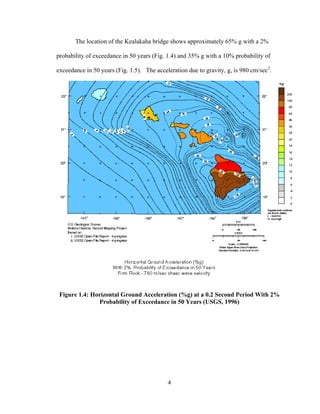
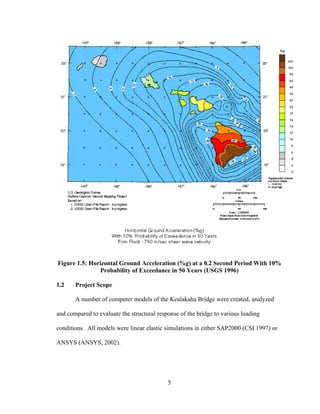
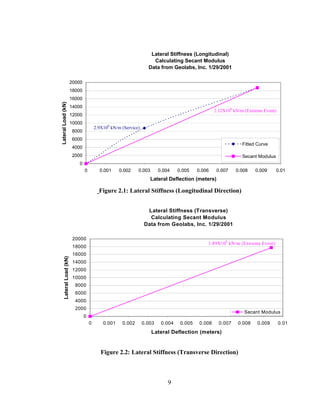
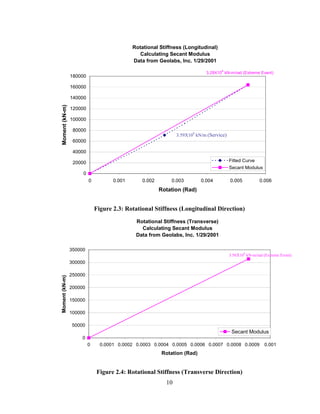
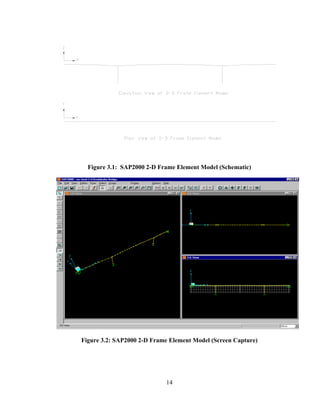
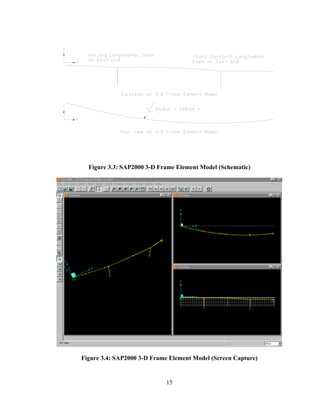
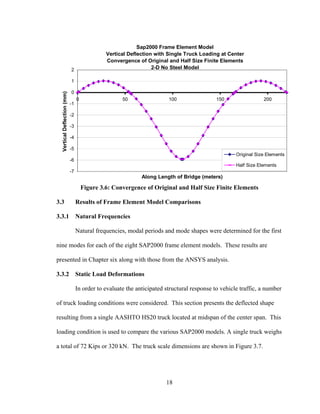
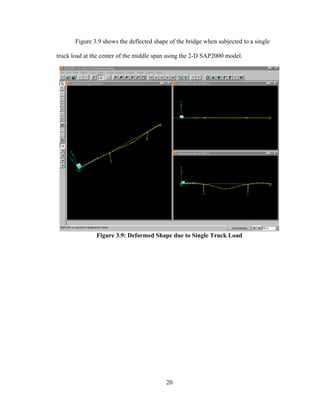
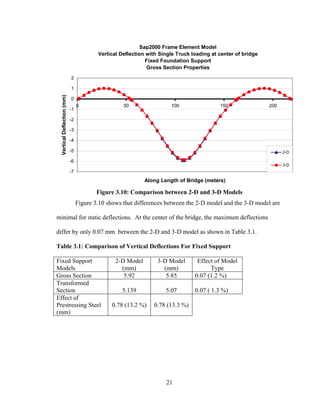
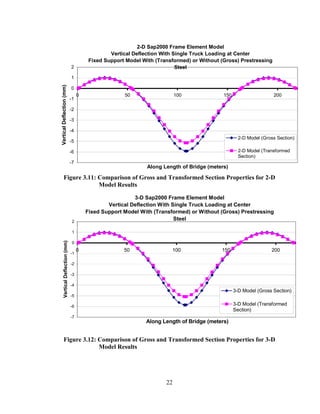
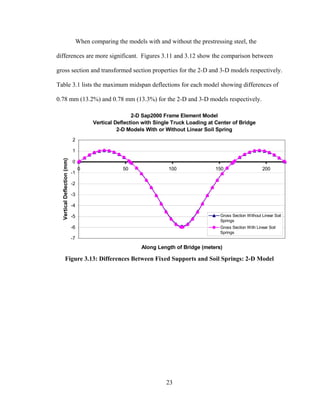
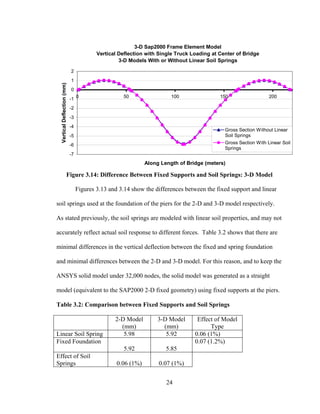
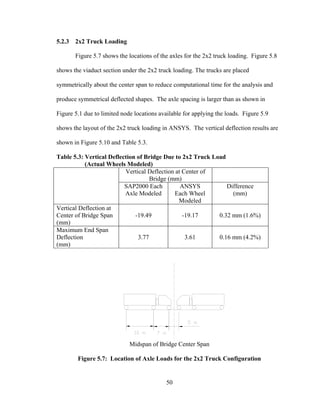
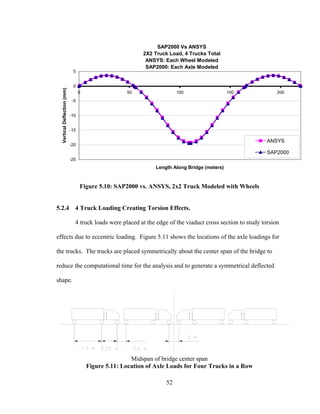
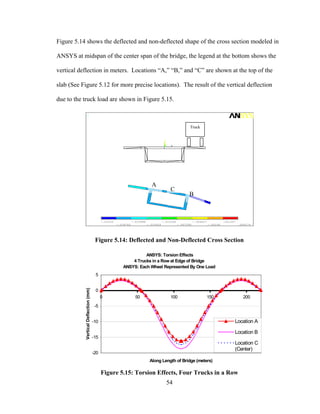
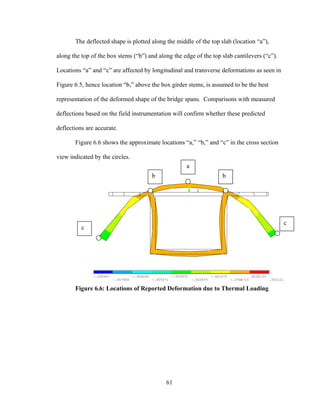
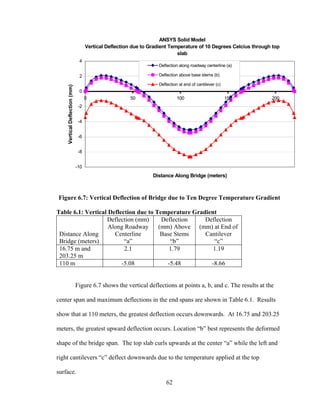
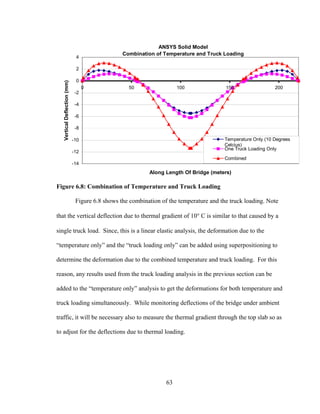
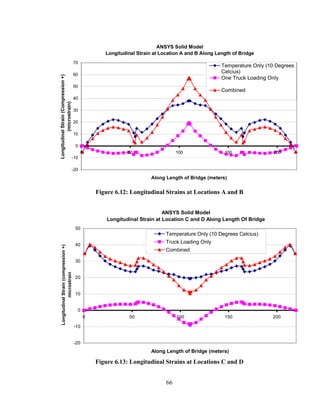
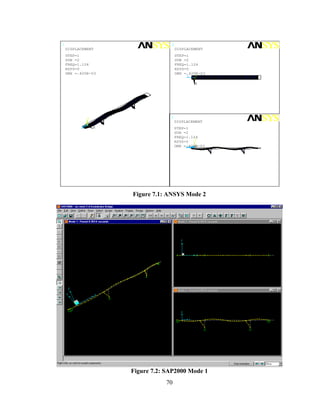
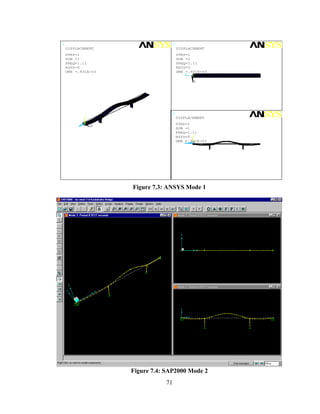
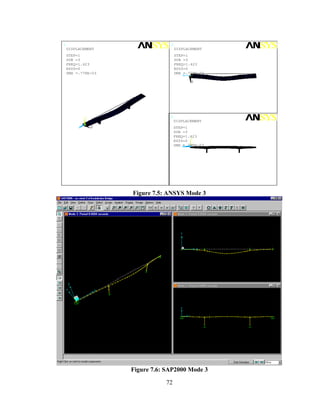
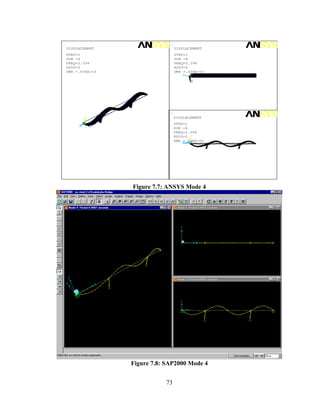
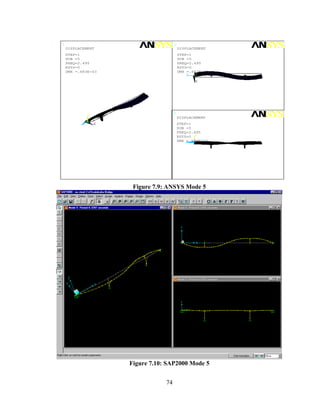
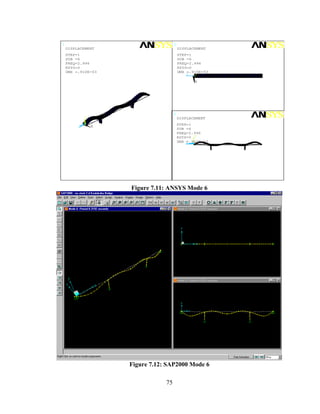
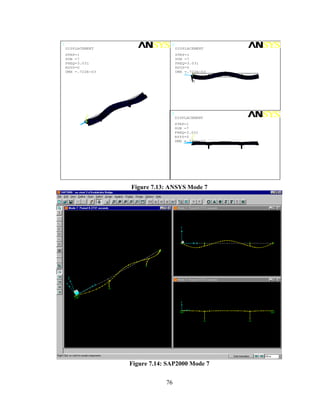
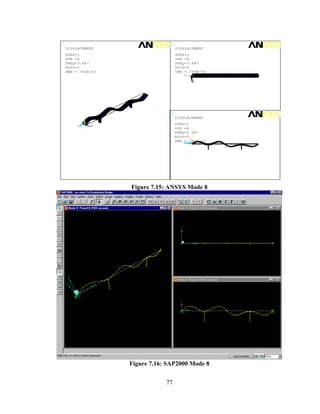
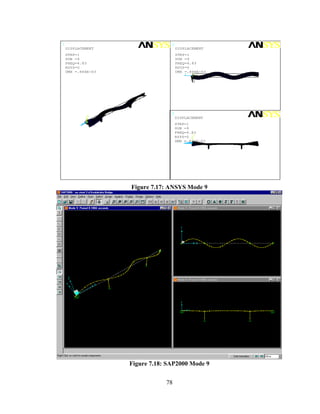
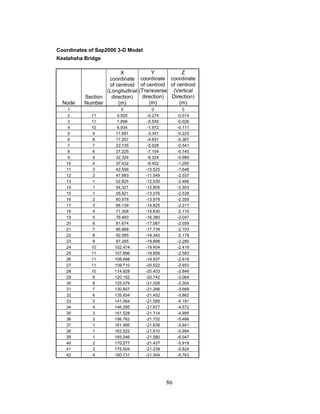
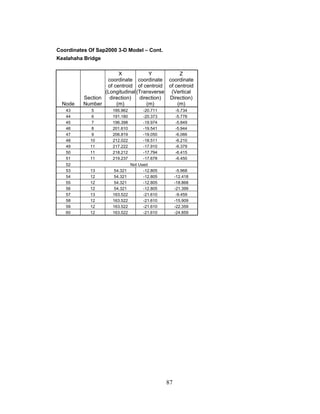
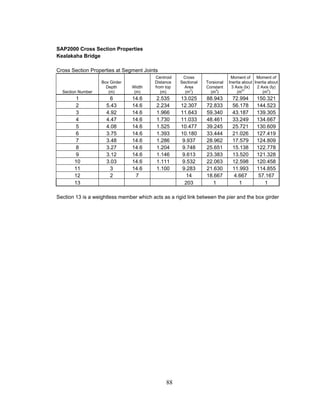
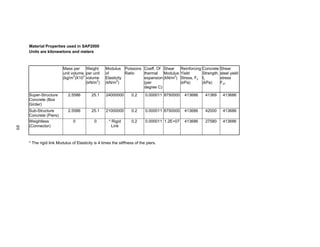
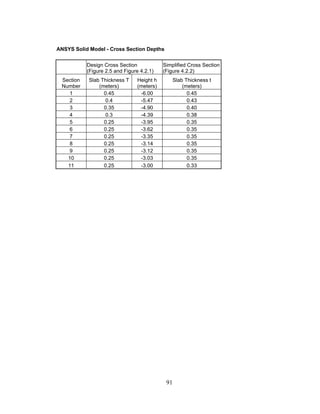
This document summarizes computer modeling of the proposed Kealakaha Stream Bridge replacement project in Hawaii. Finite element models of the bridge were created using SAP2000 and ANSYS software to analyze the bridge's behavior under various loads. A 2D and 3D frame model were made in SAP2000 and analyzed for modal frequencies and deformations from static truck loads. Additionally, a 3D solid model was made in ANSYS and analyzed for thermal loading effects, strains, modal frequencies, and deformations from static loads. The models provide predictions of the bridge's response that will be compared to sensor data collected from the actual bridge after construction.