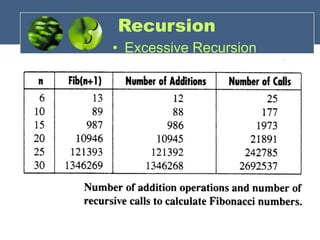
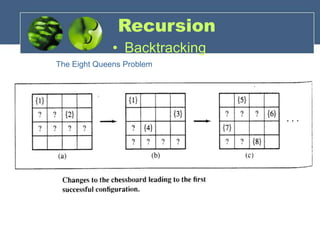
The document discusses recursion and provides examples of recursion including nested recursion. It explains recursion using functions like the Ackermann function and Fibonacci numbers. It discusses excessive recursion and how it can lead to many repeated computations. The document also covers backtracking as a method for systematically trying sequences of decisions to find a solution. It provides the example of solving the eight queens problem using backtracking and recursion.

1. Recursion
Data Structure
Submitted By:-
Dheeraj Kataria

2. A more complicated case of recursion is found in definitions in which a
function is not only defined in terms of itself but it is also used as one
of the parameters.
Example:









4if))2(2(
,4if
,0if0
)(
nnhh
nn
n
nh
h(1)=h(2+h(2))=h(14)=14
h(2)=h(2+h(4))=h(12)=12
h(3)=h(2+h(6))=h(2+6)=h(8)=8
h(4)=h(2+h(8))=h(2+8)=h(10)=10
Recursion
• Nested Recursion

3. The Ackermann function









otherwise))1,(,1(
,0,0if)1,1(
,0if1
),(
mnAnA
mnnA
nm
mnA
This function is interesting because of its remarkably rapid growth. It
grows so fast that it is guaranteed not to have a representation by a
formula that uses arithmetical operations such as addition,
multiplication, and exponentiation.
Recursion
• Nested Recursion

4. The Ackermann function









otherwise))1,(,1(
,0,0if)1,1(
,0if1
),(
mnAnA
mnnA
nm
mnA
A(0,0)=0+1=1,A(0,1)=2,A(1,0)=A(0,0)=1,
A(1,1)=A(0,A(1,0))=A(0,1)=3
A(1,2)=A(0,A(1,1))=A(0,2)=4
A(2,1)=A(1,A(2,0))=A(1,A(1,0))=A(1,1)=5
A(3,m)=A(2,A(3,m-1))=A(2,A(2,A(3,m-2)))=…=2m+3-3
32),4(
162...
2
mA
Recursion
• Nested Recursion

5. Logical simplicity and readability are used as an argument
supporting the use of recursion. The price for using recursion is slowing
down execution time and storing on the run-time stack more things
than required in a non-recursive approach.
Example: The Fibonacci numbers









.2if)1()2(
,2if1
,1if1
)(
iiFiF
i
i
iF
void Fibonacci(int n)
{
If (n<2) return 1;
else
return Fibonacci(n-1)+Fibonacci(n-2);
}
Recursion
• Excessive Recursion

6. Many repeated computations
Recursion
• Excessive Recursion

7. Recursion
• Excessive Recursion

8. void IterativeFib(int n)
{
if (n < 2)
return n;
else
{
int i = 2, tmp, current = 1, last = 0;
for ( ; i<=n; ++i)
{
tmp= current;
current += last;
last = tmp;
}
return current;
}
}
Recursion
• Excessive Recursion

9. Recursion
• Excessive Recursion

10. We can also solve this problem by using a formula discovered by
A. De Moivre.
The characteristic formula is :-
5
)
2
51
()
2
51
(
)(
nn
nf




Can be neglected
when n is large
Recursion
• Excessive Recursion
The value of is approximately -0.618034)
2
51
(


11.  Suppose you have to make a series of decisions,
among various choices, where
• You don’t have enough information to know what to
choose
• Each decision leads to a new set of choices
• Some sequence of choices (possibly more than
one) may be a solution to your problem
 Backtracking is a methodical way of trying out various
sequences of decisions, until you find one that “works”
Recursion
• Backtracking

12. Backtracking allows us to systematically try all
available avenues from a certain point after
some of them lead to nowhere. Using
backtracking, we can always return to a
position which offers other possibilities for
successfully solving the problem.
Recursion
• Backtracking

13. Recursion
• Backtracking
 Place 8 queens on an 8 by 8 chess board so
that no two of them are on the same row,
column, or diagonal
The Eight Queens Problem

14. Recursion
• Backtracking
The Eight Queens Problem

15. The Eight Queens Problem
Pseudo code of the backtracking algorithm
PutQueen(row)
for every position col on the same row
if position col is available
{
place the next queen in position col;
if (row < 8)
PutQueen(row+1);
else success;
remove the queen from position col; /* backtrack */
}
Recursion
• Backtracking

16. The Eight Queens Problem
Natural Implementation
1
Initialization
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Q
The first queen
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
0
1
0
1
1
1
1
1
0
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
1
0
1
1
0
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
Q
The second queen
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
0
Q
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
0
0
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
0
1
0
0
1
1
1
1
0
0
Recursion
• Backtracking

17. The Eight Queens Problem
Natural Implementation
Q
The third queen
0
0
0
0
0
0
0
0
0
0
1
1
0
1
1
0
Q
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
Q
0
0
0
0
0
0
0
0
1
0
0
1
1
0
0
0
1
1
0
0
1
0
0
0
1
1
1
0
0
Q
The fourth queen
0
0
0
0
0
0
0
0
0
0
Q
0
0
0
0
0
Q
0
0
0
0
0
0
0
0
0
0
1
0
1
1
0
0
Q
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
1
1
0
0
Q
The 5th & 6th queen
0
0
0
0
0
0
0
0
0
0
Q
0
0
0
0
0
Q
0
0
0
0
0
0
0
0
0
0
Q
0
0
0
0
0
Q
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Q
0
0
Have to backtrack now!This would be queen now.
Recursion
• Backtracking

18. The Eight Queens Problem
Natural Implementation
The setting and resetting part would be the most time-consuming
part of this implementation.
However, if we focus solely on the queens, we can consider the
chessboard from their perspective. For the queens, the board is not
divided into squares, but into rows, columns, and diagonals.
Recursion
• Backtracking

19. The Eight Queens Problem
Simplified data structure
A 4 by 4 chessboard Row-column = constant
for each diagonal
Recursion
• Backtracking

20. The Eight Queens Problem
Recursion
• Backtracking

21. The Eight Queens Problem
Recursion
• Backtracking

22. The Eight Queens Problem
Recursion
• Backtracking

23. Recursion
• Backtracking
The Eight Queens Problem

24. Recursion
• Backtracking
The Eight Queens Problem

25. • Usually recursive algorithms have less code,
therefore algorithms can be easier to write and
understand - e.g. Towers of Hanoi. However,
avoid using excessively recursive algorithms even
if the code is simple.
• Sometimes recursion provides a much simpler
solution. Obtaining the same result using iteration
requires complicated coding - e.g. Quicksort,
Towers of Hanoi, etc.
Why Recursion?

26. Why Recursion?
• Recursive methods provide a very natural
mechanism for processing recursive data
structures. A recursive data structure is a
data structure that is defined recursively –
e.g. Linked-list, Tree.
 Functional programming languages such as
Clean, FP, Haskell, Miranda, and SML do
not have explicit loop constructs. In these
languages looping is achieved by recursion.

27. • Recursion is a powerful problem-solving
technique that often produces very clean
solutions to even the most complex
problems.
• Recursive solutions can be easier to
understand and to describe than iterative
solutions.
Why Recursion?

28. • By using recursion, you can often write
simple, short implementations of your
solution.
• However, just because an algorithm can
be implemented in a recursive manner
doesn’t mean that it should be
implemented in a recursive manner.
Why Recursion?

29. Limitations of
Recursion
• Recursive solutions may involve extensive
overhead because they use calls.
• When a call is made, it takes time to build a
stackframe and push it onto the system stack.
• Conversely, when a return is executed, the
stackframe must be popped from the stack
and the local variables reset to their previous
values – this also takes time.

30. Limitations of
Recursion
• In general, recursive algorithms run slower
than their iterative counterparts.
• Also, every time we make a call, we must
use some of the memory resources to
make room for the stackframe.

31. Limitations of
Recursion
• Therefore, if the recursion is deep, say,
factorial(1000), we may run out of memory.
• Because of this, it is usually best to
develop iterative algorithms when we are
working with large numbers.

32. Main disadvantage of
programming recursively
• The main disadvantage of programming
recursively is that, while it makes it easier
to write simple and elegant programs, it
also makes it easier to write inefficient
ones.
• when we use recursion to solve problems we are
interested exclusively with correctness, and not
at all with efficiency. Consequently, our simple,
elegant recursive algorithms may be inherently
inefficient.