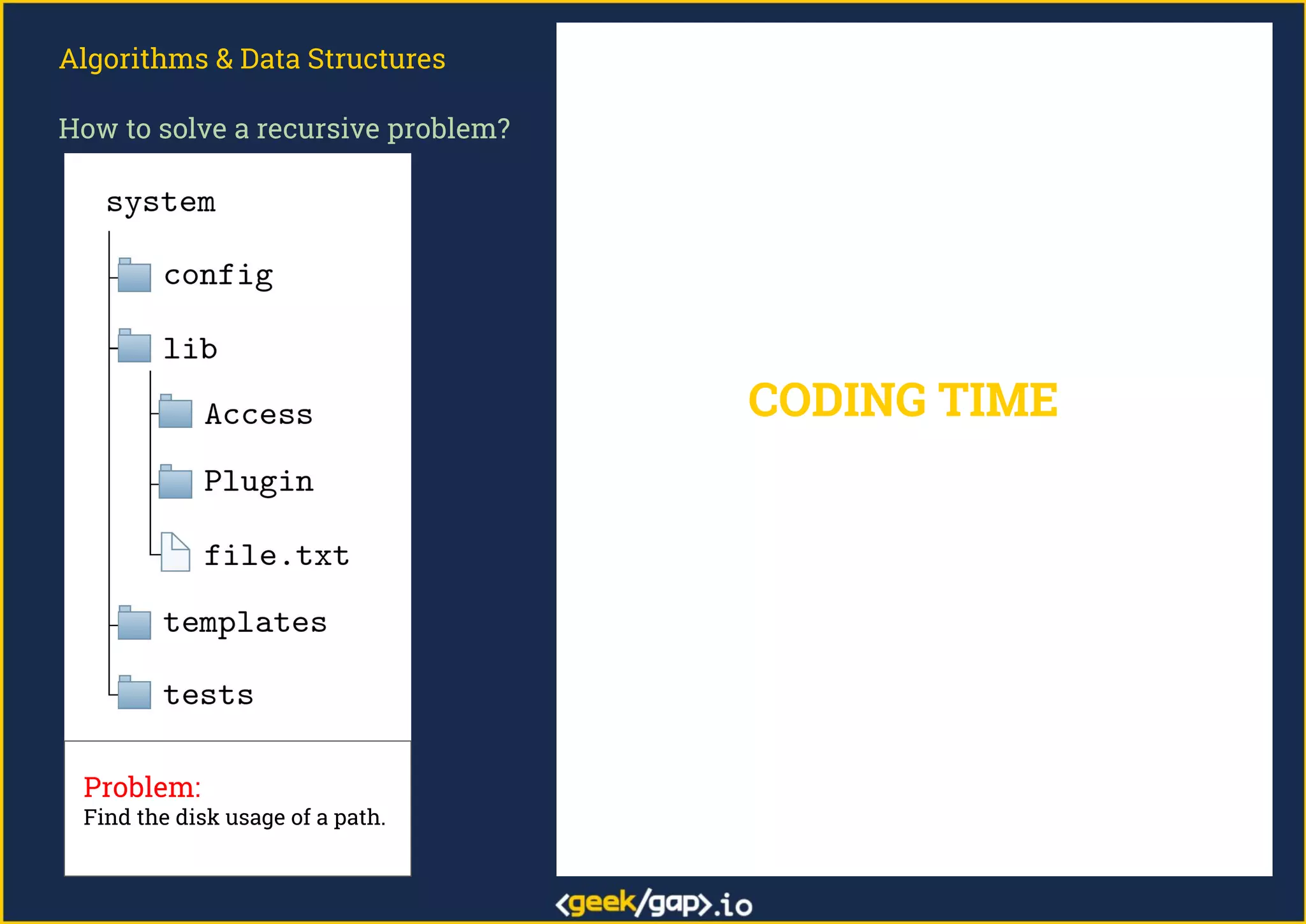
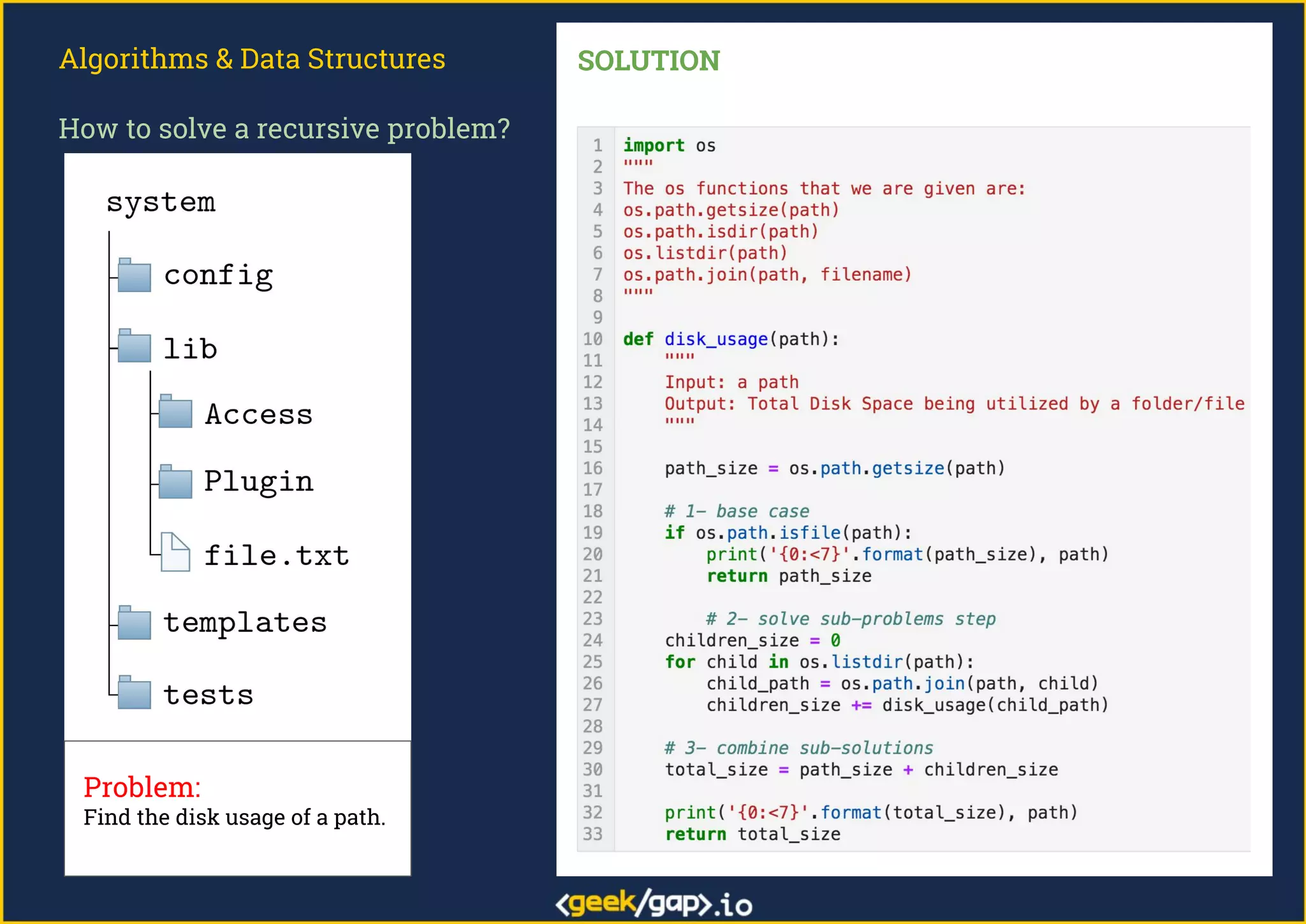
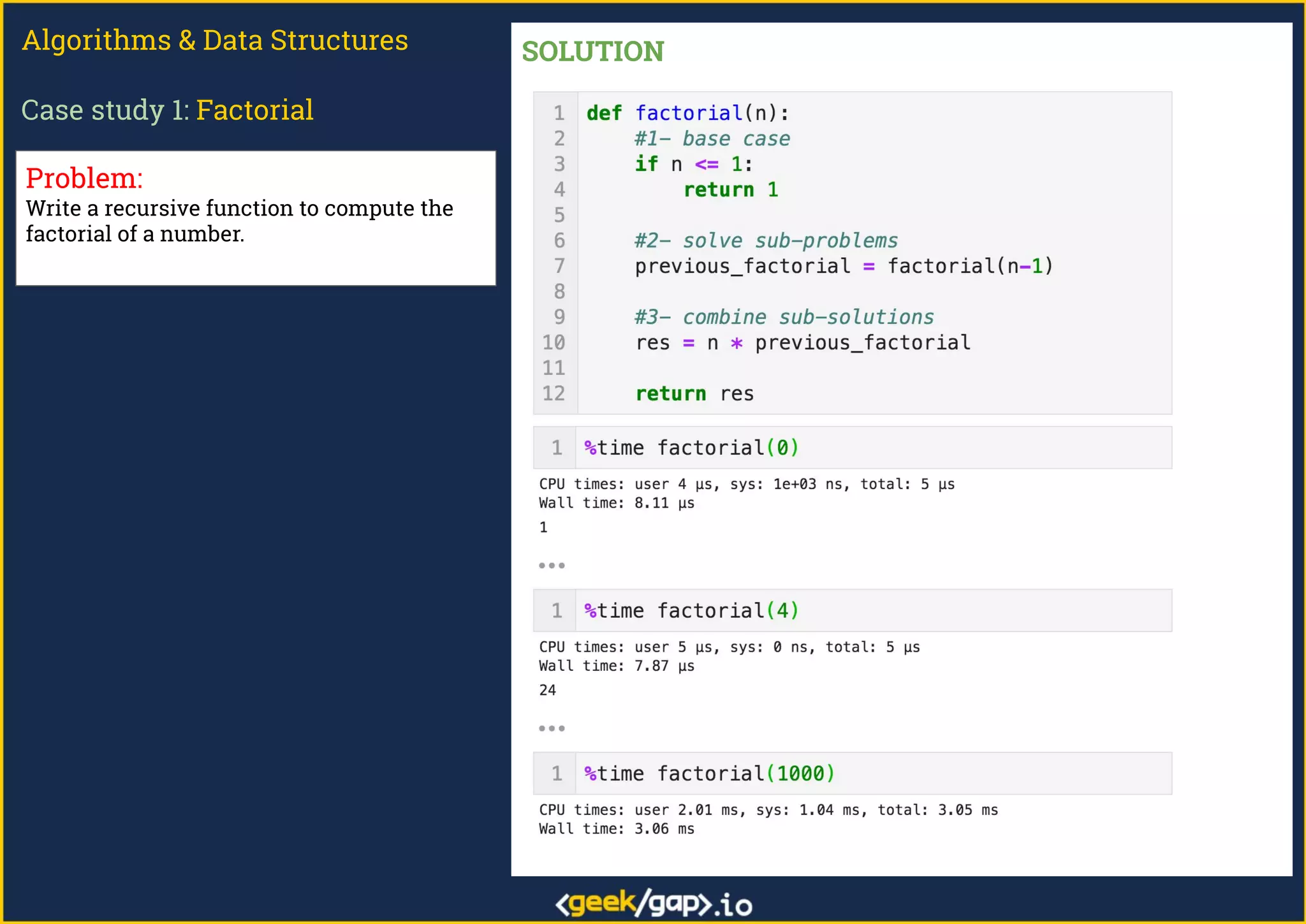
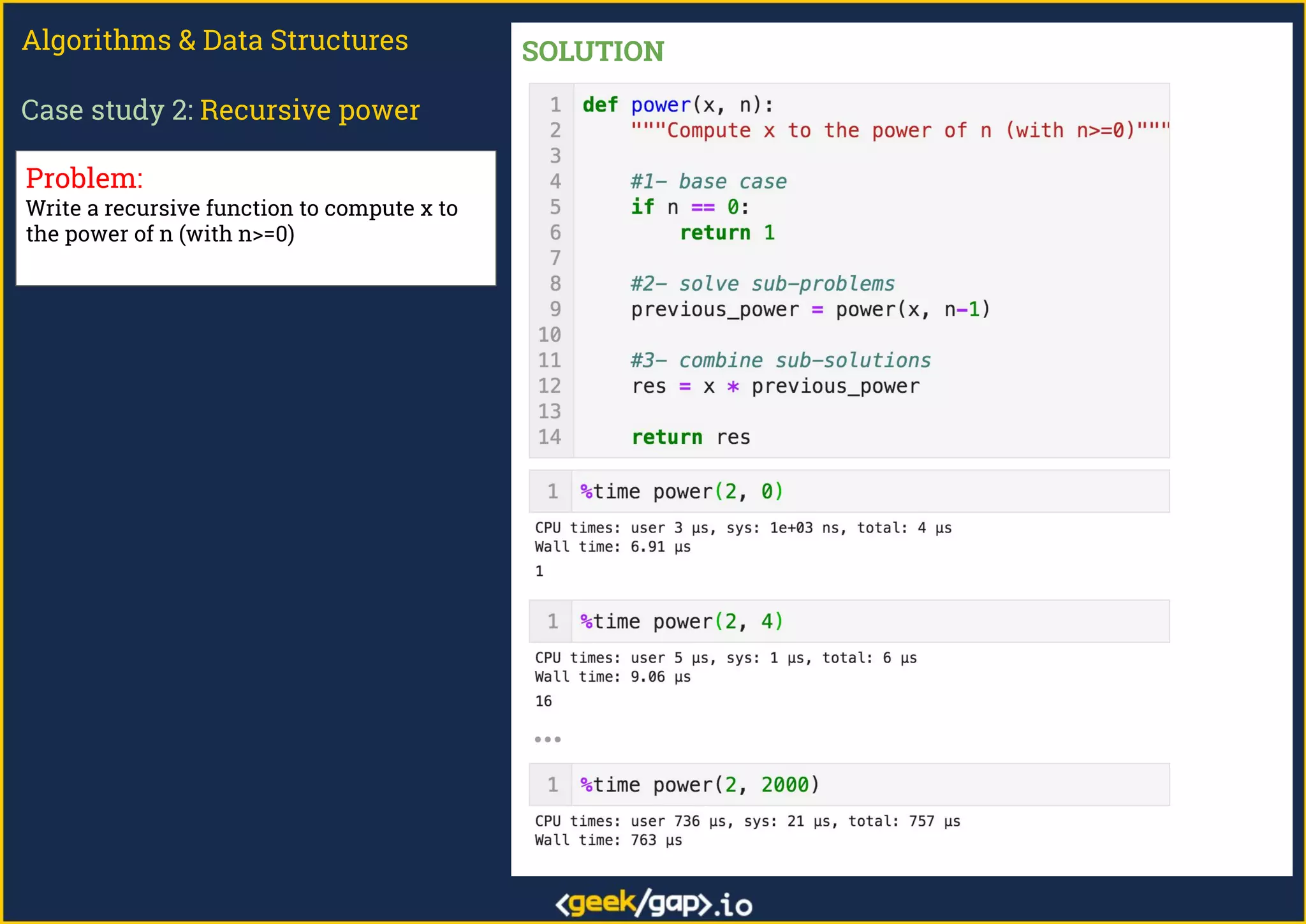
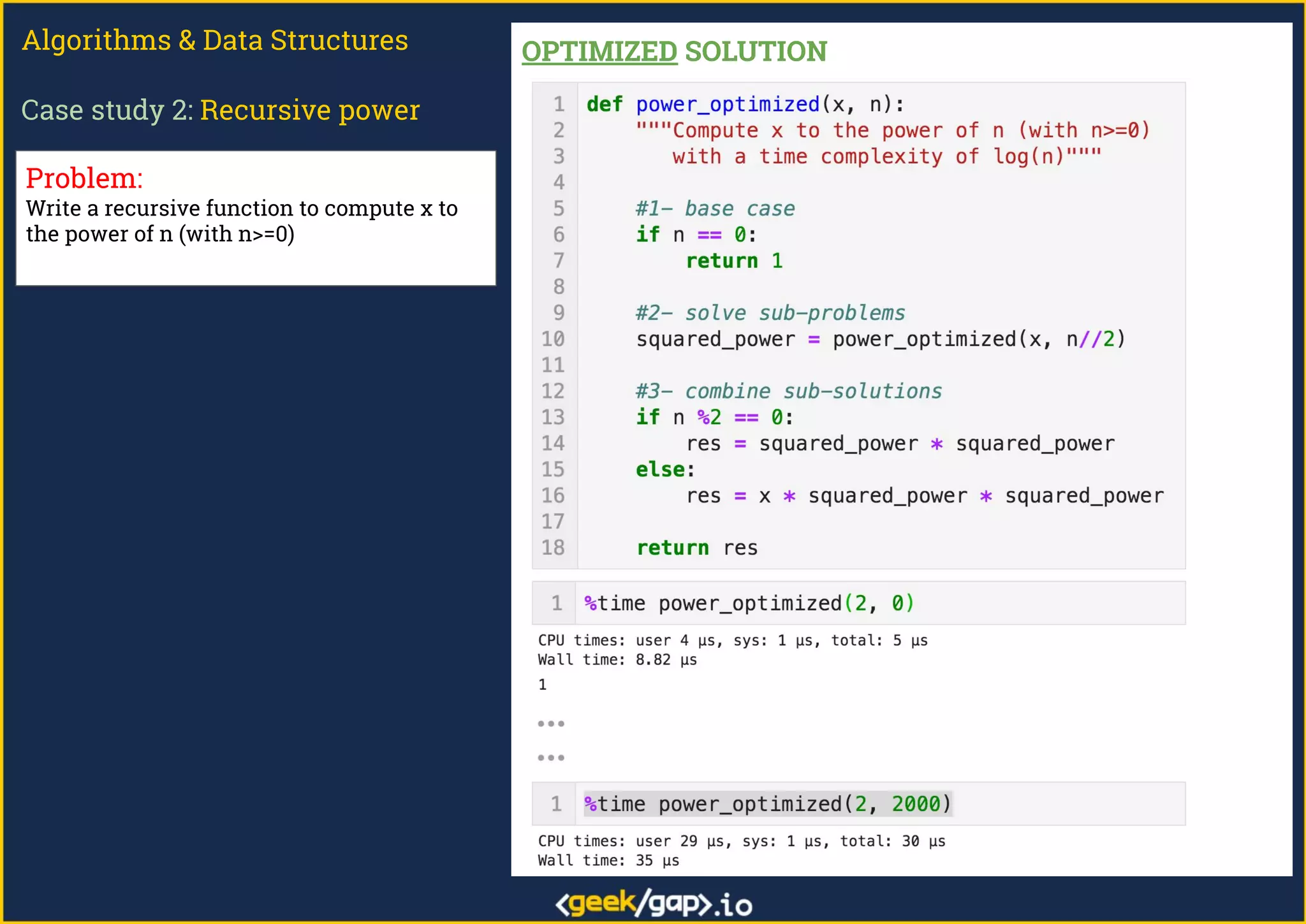
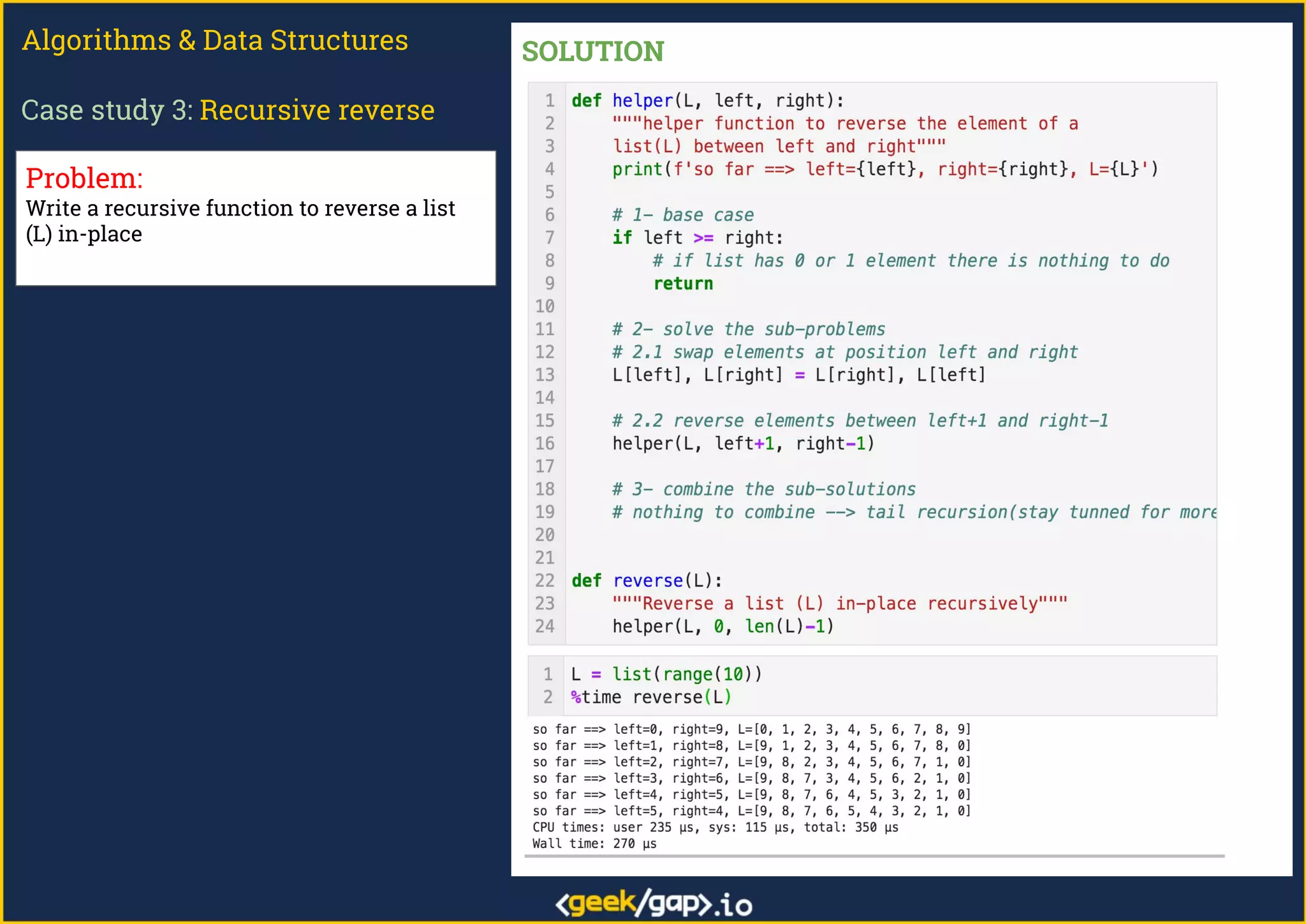
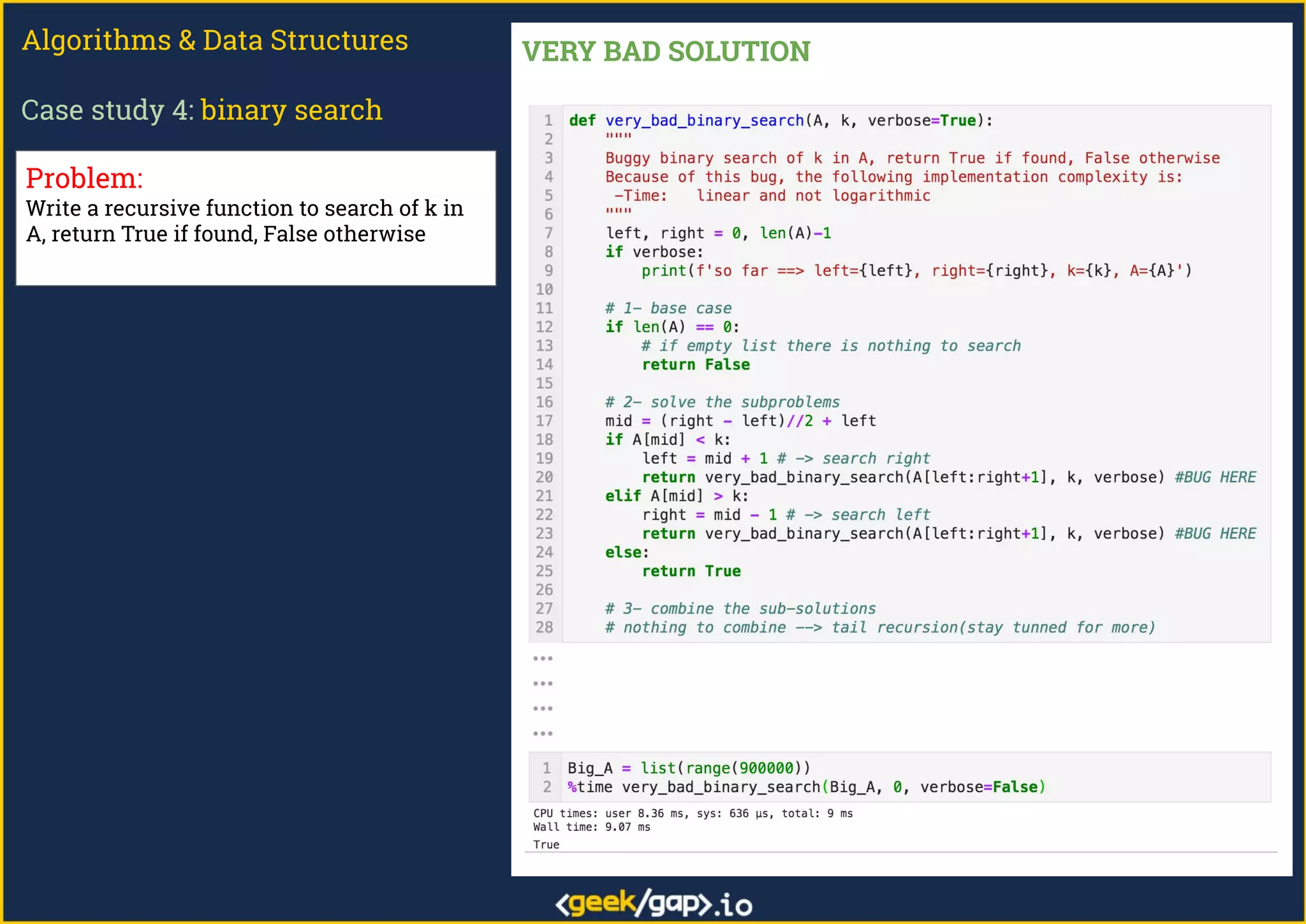
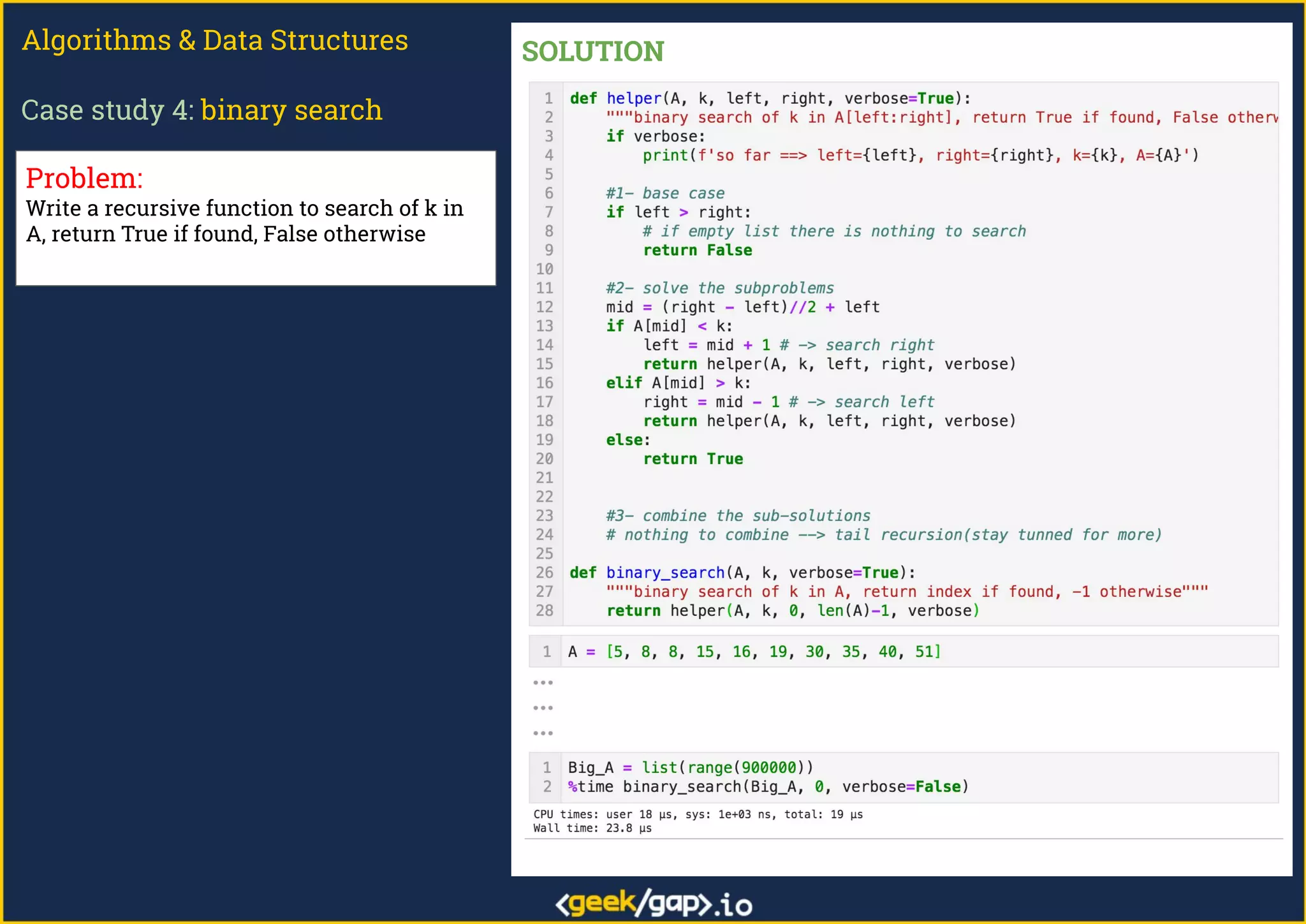
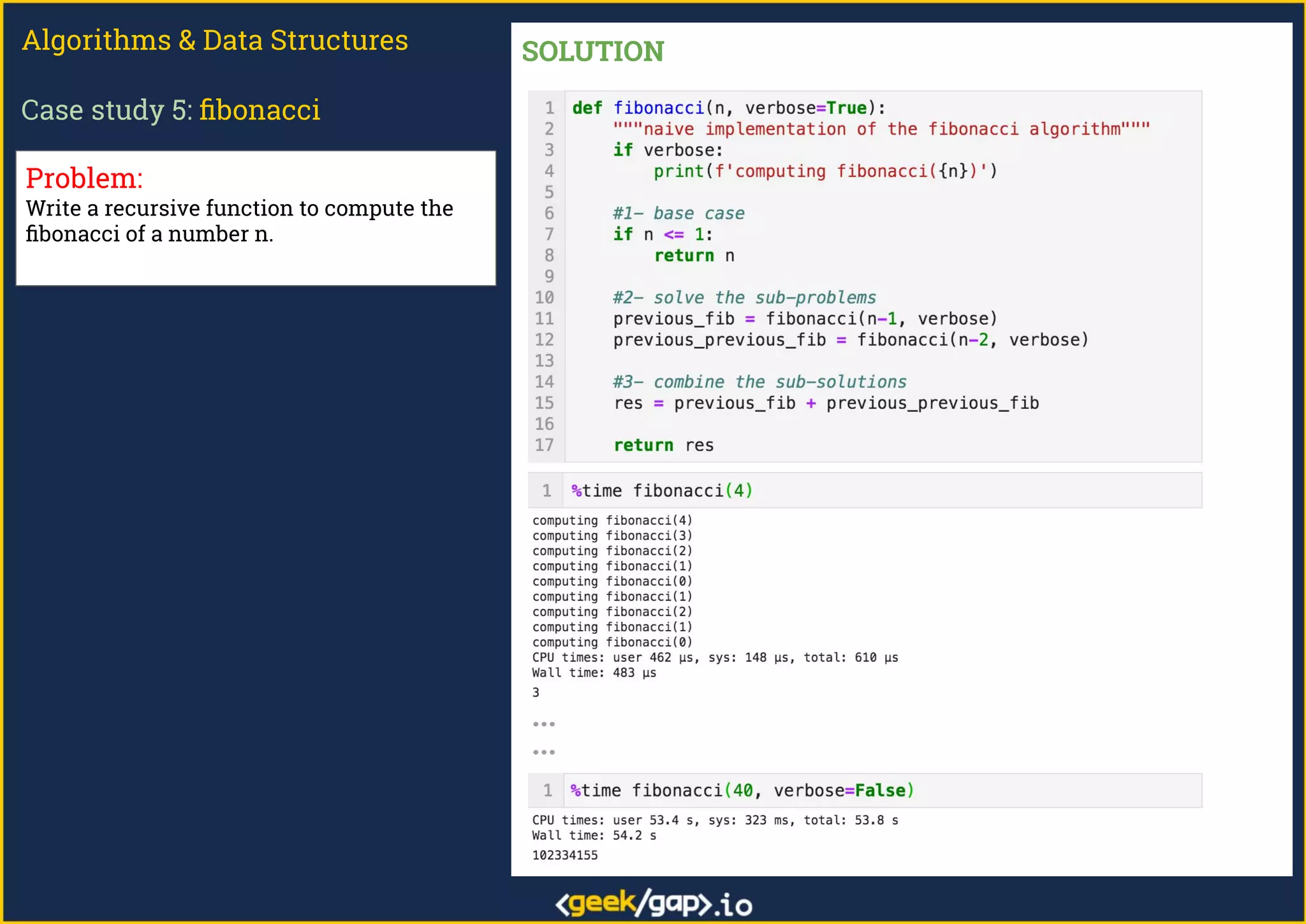
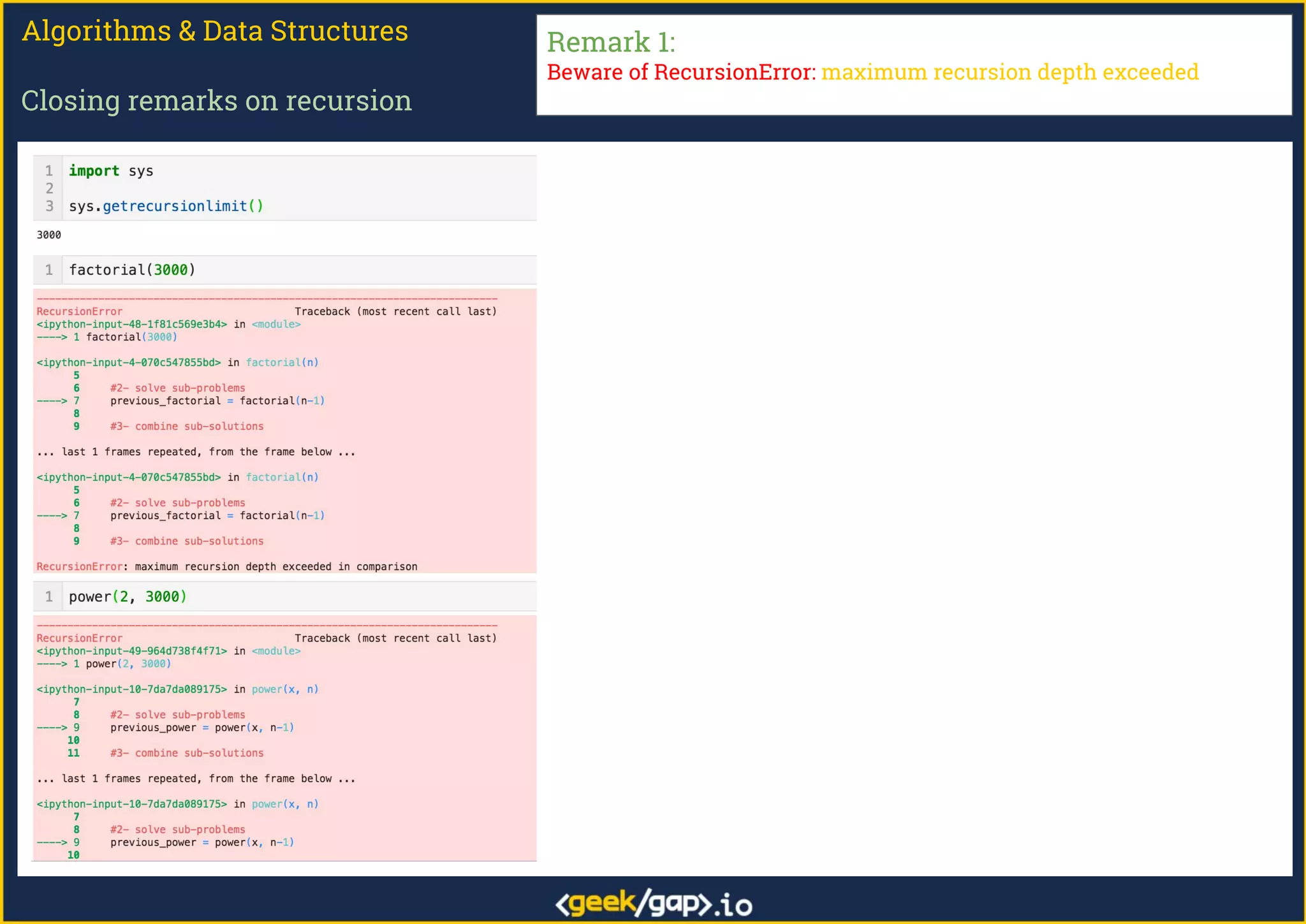
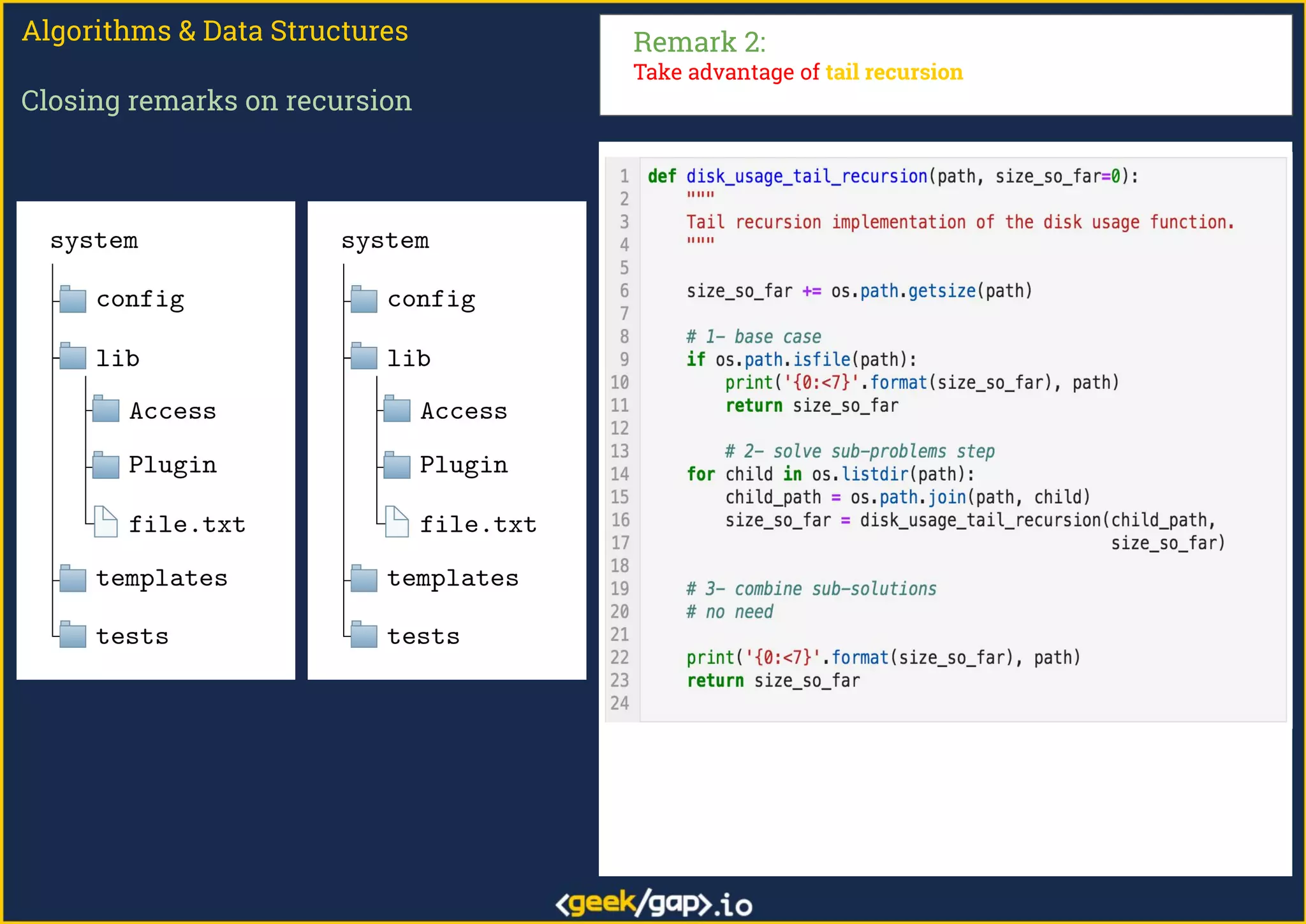
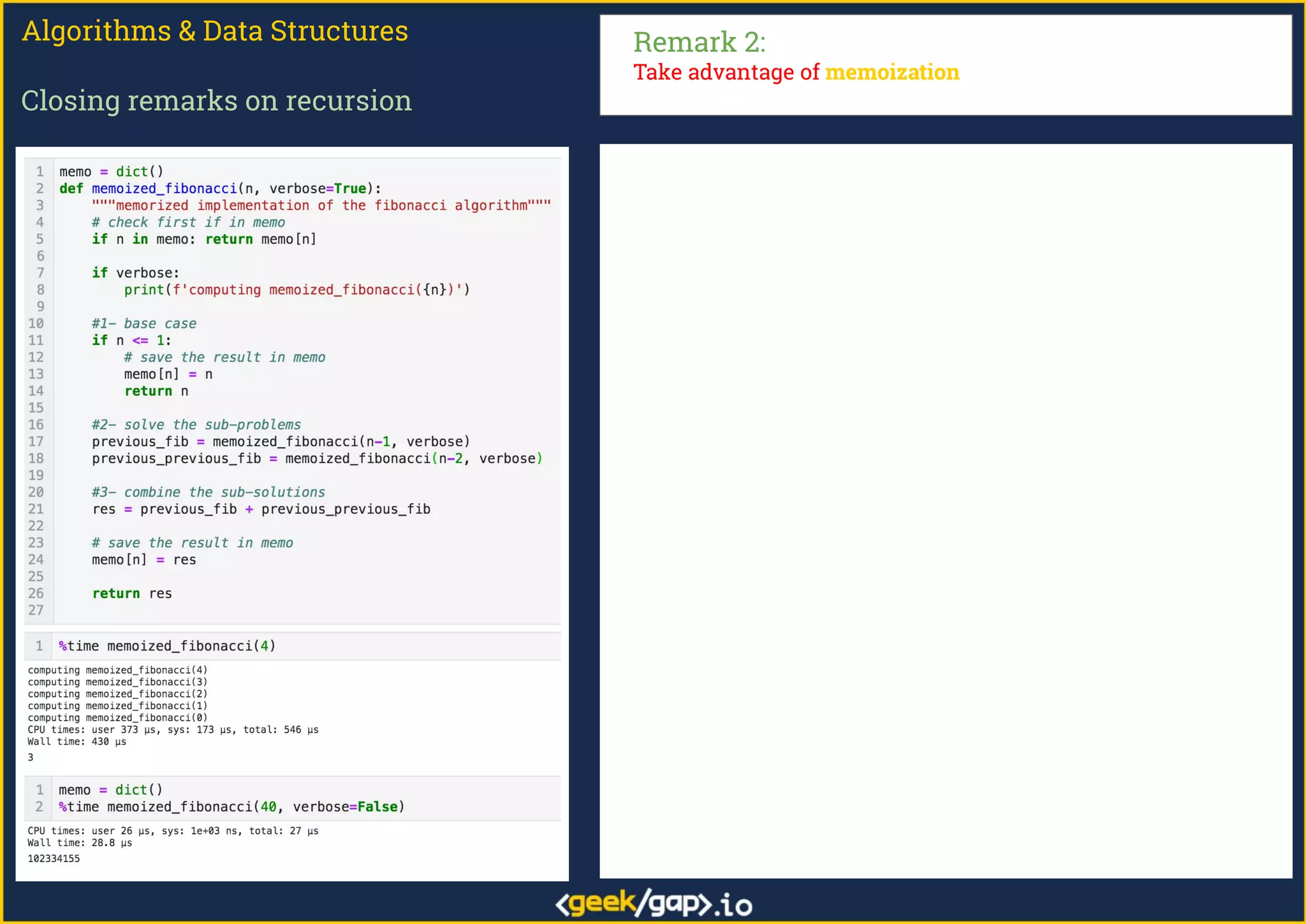
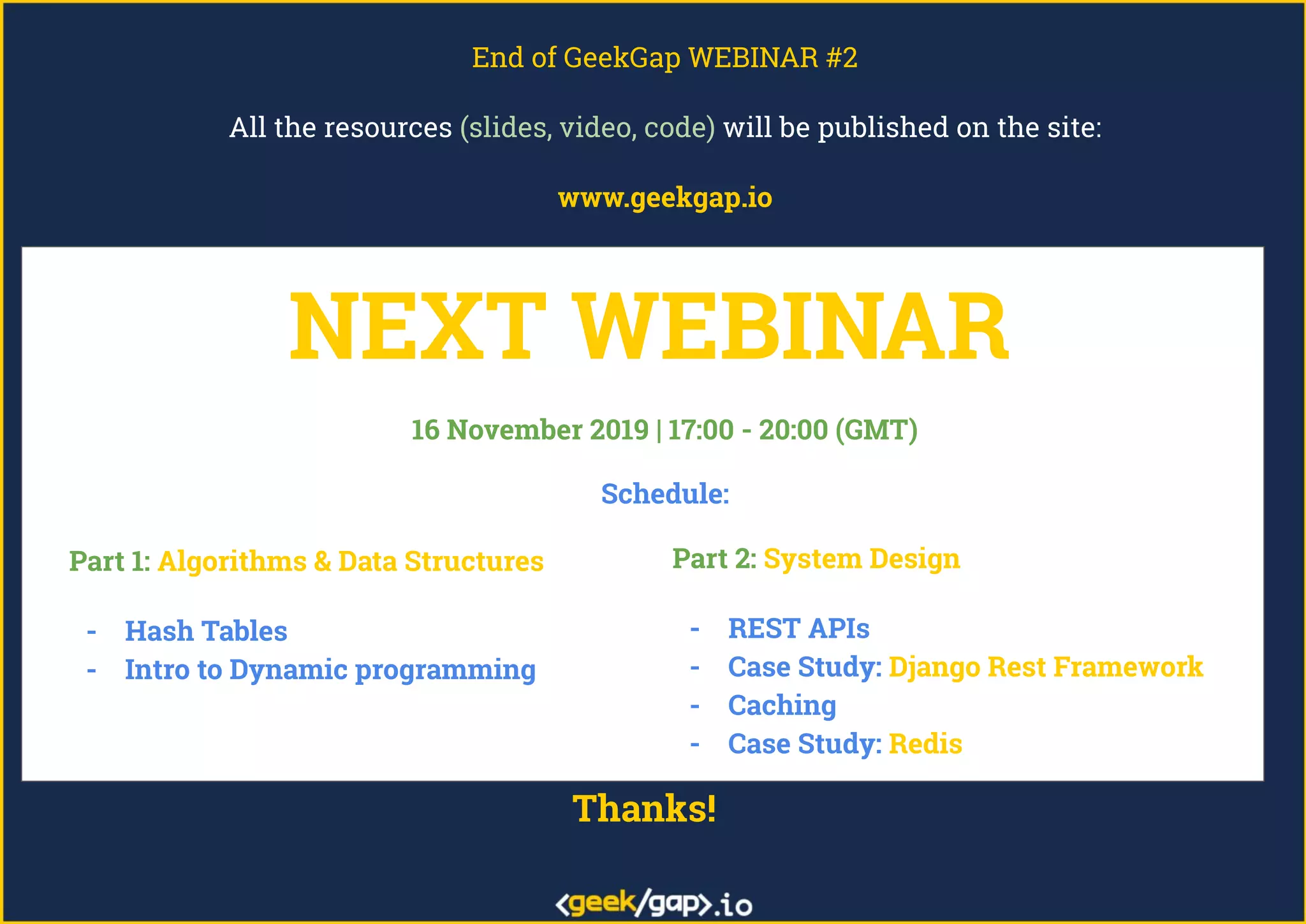
The document outlines a webinar on preparing for tech job interviews, specifically focusing on recursion in algorithms and data structures. It covers various case studies such as computing factorials, powers, reversing lists, binary search, and Fibonacci numbers, detailing problem-solving steps and coding challenges. Additionally, it emphasizes key insights on recursion, such as avoiding maximum recursion depth errors and leveraging techniques like tail recursion and memoization.